34 Divisibility Tests
Louisiana Student Standards
Standard Number |
Description of Standard |
| ### | Description |
| ### | Description |
Definition and Notation for Divisibility
Later in this module, we will explore prime numbers, composite numbers, the greatest common factor of two or more numbers, and the least common multiple of two or more numbers. Factoring is the method used to find the prime factorization of a composite number, and it can also be used to find the greatest common factor and least common multiple of a set of numbers. One of the problems in factoring large numbers is that sometimes it isn't clear if it is prime or composite. In other words, it isn't clear whether it has any factors other than [latex]1[/latex] or itself. Most of us know that if the last digit of a numeral is even, then [latex]2[/latex] will divide into it; or if it ends in [latex]0[/latex], [latex]10[/latex] will divide into it; or if it ends in [latex]0[/latex] or [latex]5[/latex], that [latex]5[/latex] will divide into it. Other than that, people may even have trouble determining if relatively small numbers are prime. For instance, many people think [latex]91[/latex] is prime, but in fact it is not ([latex]7[/latex] is one of its factors). Knowing some divisibility tests makes the task easier, so we'll soon take some time to discuss divisibility tests for several numbers. First, we need to go over the concept and notation concerning divisibility.
Definition - Divisibilility
A whole number [latex]b[/latex] is divisible by a non-zero whole number [latex]a[/latex] if there exists a whole number, [latex]n[/latex], such that [latex]a \times n[/latex] = [latex]b[/latex].
If [latex]b[/latex] is divisible by [latex]a[/latex], we call the number [latex]a[/latex] is a divisor of [latex]b[/latex].
In mathematics, the fact "[latex]b[/latex] is divisible by [latex]a[/latex]" can also be shorten as "[latex]a[/latex] divides [latex]b[/latex]," written as "[latex]a|b[/latex]".
[latex]a|b[/latex] [latex]\Longleftrightarrow[/latex] There exists a whole number, [latex]n[/latex], such that [latex]a \times n[/latex] = [latex]b[/latex].
Okay, so what exactly does "there exists a whole number, n, such that [latex]a \times n[/latex] [latex]= b[/latex]" mean? Well, it means that the first number times some whole number equals the second number. Or you can think "[latex]a[/latex] divides [latex]b[/latex]" is true if [latex]b \div a[/latex] is a whole number.
That is, [latex]a|b[/latex] tells us the divisibility of the whole number [latex]b[/latex] by its divisor [latex]a[/latex]. According to the definition, if [latex]b[/latex] is divisible by [latex]a[/latex], or [latex]a[/latex] divides [latex]b[/latex], then the divisor [latex]a[/latex] of it must also be one of its factors. In other words, here the term divisor is only used for the number that can divide the dividend evenly. As a result, in number theory, people may use "factor" and "divisor" interchangeably, considering the greatest common divisor and greatest common factor as examples. However, we should be very cautious that, in a context of division as an operation of whole numbers, the divisor of a division problem can be any non-zero number that we use to divide a given dividend.
For example, in the division problem [latex]22 \div 5[/latex], which equals [latex]4[/latex] with remainder [latex]2[/latex], we say [latex]5[/latex] is a divisor of the division. But can we say "[latex]5[/latex] is a divisor of [latex]22[/latex]"? No, because [latex]5[/latex] is not a factor of [latex]22[/latex]. In other words, we can say, [latex]22[/latex] is not divisible by [latex]5[/latex]. Intuitively, this means [latex]22[/latex] cannot be divided by [latex]5[/latex] evenly, because there is a remainder [latex]2[/latex]. We describe this fact as "[latex]5[/latex] is not a divisor of [latex]22[/latex]", written as [latex]5\not{|} 22[/latex].
More discussion on the notations for "divides" and "divided by":
When you see [latex]12/3[/latex], this means "[latex]12[/latex] divided by [latex]3[/latex]". The slash that slants to the right is another way to write the division sign, [latex]\div[/latex]. So, [latex]12/3[/latex] means the same as [latex]12 \div 3[/latex], read as "[latex]12[/latex] divided by [latex]3[/latex]". It is a solvable division problem with [latex]4[/latex] as its answer: [latex]12 \div 3[/latex] = [latex]4[/latex]. We read this equation as a statement "[latex]12[/latex] divided by [latex]3[/latex] equals 4." From a linguistic perspective, "[latex]12 \div 3[/latex]", as a number described by a prepositional phrase, serves as the subject of the statement, "[latex]=[/latex]" as the verb, and the answer [latex]4[/latex] is the object.
Differently, if I say "[latex]3[/latex] divides [latex]12[/latex]", I am making a stand alone statement, "[latex]3[/latex] divides [latex]12[/latex]," in which the subject is [latex]3[/latex], "divides" is the verb, and [latex]12[/latex] is the object. It is not a division problem that needs to be solved. It is a statement that happens to be true. The symbol used to represent the verb "divides" is a vertical line. So, "[latex]3[/latex] divides [latex]12[/latex]" can be written "[latex]3|12[/latex]". Again, this is a statement, a fact, not a division problem. The way to express "does not divide" is to put a slash through the symbol: [latex]\not{|}[/latex].
How to decide if a number divides another number?
Let's get back to why "[latex]3[/latex] divides [latex]12[/latex]" is a true statement. According to the definition, you can be formal and ask yourself:
Is there a whole number [latex]n[/latex] such that [latex]3 \times n[/latex] = [latex]12[/latex]?
Or, you can simply ask yourself:
Is [latex]3[/latex] a factor (or divisor) of [latex]12[/latex]?
In either case, the answer is yes, so the statement is true. In Example 1 below, we will practice more of the terms "divides" and "divisible".
Example 1 - "Divides" and "Divisible"
Determine if the following statement is true or false and back up your answer.
a. [latex]16[/latex] is divisible by [latex]8[/latex].
Solution:
This is a true statement because [latex]8 \times 2 = 16[/latex] and this shows that [latex]8[/latex] is a factor of [latex]16[/latex]. We can say this statement as "[latex]8[/latex] divides [latex]16[/latex]". In other words, [latex]16[/latex] is divisible by [latex]8[/latex].
b. [latex]6[/latex] divides [latex]20[/latex].
Solution:
This is a false statement because [latex]6[/latex] is not a factor of [latex]20[/latex], and therefore, [latex]6[/latex] does not divide [latex]20[/latex]. In other words, [latex]20[/latex] is not divisible by [latex]6[/latex].
c.
Solution:
This is a true statement because [latex]3 \times 7 = 21[/latex] and this shows that [latex]3[/latex] is a factor of [latex]21[/latex]. We can say this statement as "[latex]3[/latex] divides [latex]21[/latex]". In other words, [latex]21[/latex] is divisible by [latex]3[/latex].
Let's work a little more on the difference between a statement using "divides", and an actual division problem, especially when the math notations are used. The example below helps us practice more using the symbol [latex]|[/latex]for "divides" and [latex]/[/latex] for "divided by". For each item in the example, you can read the given numbers and symbols in between, then decide its meaning.
Example 2 - "Divides" or "Divided by"
Determine if each of the following is a statement or if it is a division problem. If it is a statement, state if it is true or false and back up your answer. If it is a division problem, state the answer to the division problem.
a. [latex]4|20[/latex]
Solution:
This should be read as "[latex]4[/latex] divides [latex]20[/latex]". It is a statement. It is true, because [latex]4[/latex] is a factor of [latex]20[/latex] since [latex]4 \times 5 = 20[/latex].
b. [latex]20/6[/latex]
Solution:
This should be read as "[latex]20[/latex] divided by [latex]6[/latex]". It is a division problem. The answer is [latex]3[/latex] with remainder [latex]2[/latex].
c. [latex]15|3[/latex]
Solution:
This should be read as "[latex]15[/latex] divides [latex]3[/latex]". It is a statement. It is false, because [latex]15[/latex] is not a factor of [latex]3[/latex] instead, [latex]3[/latex] is a factor of [latex]15[/latex].
Exercise 1
Determine if each of the following is a statement or if it is a division problem. If it is a statement, then decide if it is true or false and back up your answer. If it is a division problem, state the answer to the division problem. Study the examples on the previous page if you need help getting started.
a. [latex]35/7[/latex]
Solution
We read this as “[latex]35[/latex] divided by [latex]7[/latex]”. It is a division problem. The answer is [latex]5[/latex].
b. [latex]35|7[/latex]
Solution
We read this as “[latex]35[/latex] divides [latex]7[/latex]”. It is a statement. It is false because [latex]35[/latex] is not a factor of [latex]7[/latex]. Instead, [latex]7[/latex] is a factor of [latex]35[/latex], so “[latex]7[/latex] divides [latex]35[/latex]” or “[latex]7|35[/latex]” is a true statement.
c. [latex]7|35[/latex]
Solution
We read this as “[latex]7[/latex] divides [latex]35[/latex]”. It is a statement. It is true because [latex]7[/latex] is a factor of [latex]35[/latex]: [latex]7 \times 5 = 35[/latex]
d. [latex]40/7[/latex]
Solution
We read this as “[latex]40[/latex] divided by [latex]7[/latex]”. It is a division problem. The answer is [latex]5[/latex] with remainder [latex]5[/latex].
e. [latex]56|8[/latex]
Solution
We read this as “[latex]56[/latex] divides [latex]8[/latex]”. It is a statement. It is false because [latex]56[/latex] is not a factor of [latex]8[/latex]. Instead, [latex]8[/latex] is a factor of [latex]56[/latex], so “[latex]8[/latex] divides [latex]56[/latex]” or “[latex]8|56[/latex]” is a true statement.
f. [latex]7|40[/latex]
Solution
We read this as “[latex]7[/latex] divides [latex]40[/latex]”. It is a statement. It is false because [latex]7[/latex] is not a factor of [latex]40[/latex].
g. [latex]12[/latex] divides [latex]60[/latex]
Solution
This is a statement. It is true because [latex]12[/latex] is a factor of [latex]60[/latex]: [latex]12 \times 5 = 60[/latex].
h. [latex]80[/latex] divided by [latex]30[/latex]
Solution
This is a division problem. The answer is [latex]2[/latex] with remainder [latex]20[/latex].
i. [latex]70[/latex] divided by [latex]5[/latex]
Solution
This is a division problem. The answer is [latex]14[/latex] and remainder is [latex]0[/latex]. So, we can make a statement about the divisibility of [latex]70[/latex] by [latex]5[/latex]: [latex]70[/latex] is divisible by [latex]5[/latex], or [latex]5[/latex] divides [latex]70[/latex], or [latex]5|70[/latex].
j. [latex]42[/latex] divides [latex]3[/latex]
Solution
This is a statement. It is false because [latex]42[/latex] is not a factor of [latex]3[/latex]. Instead, [latex]3[/latex] is a factor of [latex]42[/latex], so “[latex]3[/latex] divides [latex]42[/latex]” or “[latex]3|42[/latex]” is a true statement.
k. [latex]6[/latex] divides [latex]42[/latex]
Solution
This is a statement. It is true because [latex]6[/latex] is a factor of [latex]42[/latex]: [latex]6 \times 7 = 42[/latex].
l. [latex]80[/latex] divided by [latex]10[/latex]
Solution
This is a division problem. The answer is [latex]8[/latex] and remainder is [latex]0[/latex]. So, we can make a statement about the divisibility of [latex]80[/latex] by [latex]10[/latex]: [latex]80[/latex] is divisible by [latex]10[/latex], or [latex]10[/latex] divides [latex]80[/latex], or [latex]10|80[/latex].
m. [latex]100/2[/latex]
Solution
We read this as “[latex]100[/latex] divided by [latex]2[/latex]”. It is a division problem. The answer is [latex]50[/latex].
n. [latex]4|100[/latex]
Solution
We read this as “[latex]4[/latex] divides [latex]100[/latex]”. It is a statement. It is true because [latex]4[/latex] is a factor of [latex]100[/latex]: [latex]4 \times 25 = 100[/latex]
o. [latex]4|90[/latex]
Solution
We read this as “[latex]4[/latex] divides [latex]90[/latex]”. It is a statement. It is false because [latex]4[/latex] is not a factor of [latex]90[/latex].
p. [latex]25|5[/latex]
Solution
We read this as “[latex]25[/latex] divides [latex]5[/latex]”. It is a statement. It is false because [latex]25[/latex] is not a factor of [latex]5[/latex]. Instead [latex]5[/latex] is a factor of [latex]25[/latex], so “[latex]5[/latex] divides [latex]25[/latex]” or “[latex]5|25[/latex]” is a true statement.
Properties and Proofs about Divisibility
Below, we will discuss properties of divisibility and do some proofs for them. Before doing so, let's go back to the formal definition of "divides":
[latex]a|b[/latex] if there exists a whole number, [latex]n[/latex], such that [latex]an = b[/latex].
We need to use this formal notation in order to do some proofs.
Key Takeaway - Sum Property of Divisibility
[latex]a[/latex] is a non-zero whole number, [latex]b[/latex] and [latex]c[/latex] are any whole numbers.
- If [latex]a|b[/latex] and [latex]a|c[/latex], then [latex]a|(b+c)[/latex].
- If [latex]a|b[/latex] and [latex]a\not{|} c[/latex], then [latex]a\not{|} (b+c)[/latex].
How can we know the property is true? [latex]a|b[/latex] and [latex]a|c[/latex]means that [latex]a[/latex] is a factor of [latex]b[/latex] and [latex]a[/latex] is also a factor of [latex]c[/latex]. To determine if that necessarily implies that [latex]a[/latex] is also a factor of the sum, [latex]b + c[/latex], we look at two steps.
The first line of strategy is to test it out on a few numbers and see if we can find a counterexample. If we find a counterexample, the answer is no, and we are done. If we can't find a counterexample, then it is likely to be true. If we think it is true, then we must PROVE it by being general, that is, to show it is true not only for the numbers we test, but for all numbers.
Let's start by picking any number for [latex]a[/latex], like [latex]a = 3[/latex], and then choose numbers for [latex]b[/latex] and [latex]c[/latex] for which [latex]3[/latex] is a factor, such as [latex]15[/latex] and [latex]18[/latex]. Plug them in: "If [latex]3|15[/latex] and [latex]3|18[/latex], does [latex]3|(15+18)[/latex]?" Since [latex]3|33[/latex], the answer is yes. It looks like this statement might be true, although we cannot make an argument by only testing this one set of numbers. Exercise 2 below guides you to do more testing with more numbers.
Exercise 2
Choose different numbers for [latex]a[/latex], [latex]b[/latex] and [latex]c[/latex] in the statement "If [latex]a|b[/latex] and [latex]a|c[/latex], then [latex]a|(b + c)[/latex]" to see if the statement seems to be true.
(Solutions will vary based on the numbers chosen.)
a. If we choose [latex]a = 4[/latex], what can we choose for [latex]b[/latex] and [latex]c[/latex]? Is this statement true?
Solution
If [latex]a = 4[/latex] then we can let [latex]b = 8[/latex] and [latex]c = 12[/latex].
Now [latex]4|8[/latex] and [latex]4|12[/latex] so [latex]4|(8 + 12) \rightarrow 4|20[/latex]. Since [latex]4[/latex] does divide [latex]20[/latex], the statement is true.
b. If we choose [latex]a = 7[/latex], what can we choose for [latex]b[/latex] and [latex]c[/latex]? Is this statement true?
Solution
If [latex]a = 7[/latex] then we can let [latex]b = 14[/latex] and [latex]c = 21[/latex].
Now [latex]7|14[/latex] and [latex]7|21[/latex] so [latex]7|(14 + 21) \rightarrow 7|35[/latex]. Since [latex]7[/latex] does divide [latex]35[/latex], the statement is true.
c. If we choose [latex]a = 11[/latex], what can we choose for [latex]b[/latex] and [latex]c[/latex]? Is this statement true?
Solution
If [latex]a = 11[/latex] then we can let [latex]b = 22[/latex] and [latex]c = 33[/latex].
Now [latex]11|22[/latex] and [latex]11|33[/latex] so [latex]11|(22 + 33) \rightarrow 11|55[/latex]. Since [latex]11[/latex] does divide [latex]55[/latex], the statement is true.
For all our choices, the statement, "If [latex]a|b[/latex] and [latex]a|c[/latex], then [latex]a|(b + c)[/latex]", happens to be true. Now, to argue that it is always true, we must write a proof to prove it. Below is one way to write a formal proof.
Prove the following statement is true: If [latex]a|b[/latex] and [latex]a|c[/latex], then [latex]a|(b + c)[/latex].
Proof:
If [latex]a|b[/latex], then [latex]an = b[/latex] for some whole number, [latex]n[/latex]. If [latex]a|c[/latex], then [latex]am = c[/latex] for some whole number, [latex]m[/latex]. Using these substitutions for [latex]b[/latex] and [latex]c[/latex], we get that [latex]a|(b + c)[/latex] is true if [latex]a|(an + am)[/latex] which is true if [latex]a[/latex] is a factor of [latex]an + am[/latex]. Factor: [latex]an + am = a(n + m)[/latex]. This clearly shows that [latex]a[/latex] is indeed a factor of [latex]an + am[/latex]. Therefore, if [latex]a|b[/latex] and [latex]a|c[/latex], then [latex]a|(b + c)[/latex].
Is the following statement true? If [latex]a|(b + c)[/latex], then [latex]a|b[/latex] and [latex]a|c[/latex].
[latex]a|(b + c)[/latex] means that [latex]a[/latex] is a factor of the sum, [latex]b + c[/latex]. The question asks if that necessarily implies that [latex]a[/latex] is a factor of [latex]b[/latex] and also a factor of [latex]c[/latex]. The first line of strategy is to test it out on a few numbers and see if you can find a counterexample or if it looks like it is true. If you find a counterexample, the answer is no, and you are done. If you think it is true, you must PROVE it by being general and formal.
Start by picking any number for [latex]a[/latex], like [latex]a = 3[/latex] and picking a number for the sum [latex]b + c[/latex], for which [latex]3[/latex] is a factor, like [latex]15[/latex] or [latex]18[/latex], etc. Let [latex]b + c = 15[/latex]. Note that there are many combinations of numbers that add up to [latex]15: 1 + 14, 2 + 13, 3 + 12, 7 + 8[/latex], etc. You are being asked if [latex]3[/latex] divides into the sum of any two whole numbers, will it necessarily divide into each individual addend as well? For instance, if you broke [latex]15[/latex] up as the sum of [latex]9[/latex] and [latex]6[/latex], this would be the statement: "If [latex]3|(9 + 6)[/latex], then [latex]3|9[/latex] and [latex]3|6[/latex]." Using these numbers, it is true, and you haven't found a counterexample. Try splitting up [latex]15[/latex] another way, perhaps as the sum of [latex]10[/latex] and [latex]5[/latex]. Then, the statement becomes: "If [latex]3|(10 + 5)[/latex], then [latex]3|10[/latex] and [latex]3|5[/latex]." The answer is no, and therefore these numbers may be used as a counterexample, which proves the statement is false. Remember: In order for a statement to be true, it must be for all values of [latex]a[/latex] and [latex]b[/latex]. On the other hand, only one counterexample showing it is not true is sufficient to prove a statement is false. As a conclusion, the statement "If [latex]a|(b + c)[/latex], then [latex]a|b[/latex] and [latex]a|c[/latex]." is false.
Similar to the sum property of divisibility, we can conclude the product property of divisibility as below.
Key Takeaway - Product Property of Divisibility
[latex]a[/latex] is a non-zero whole number, [latex]b[/latex] and [latex]c[/latex] are any whole numbers.
- If [latex]a|b[/latex] and [latex]a|c[/latex], then [latex]a|(bc)[/latex].
- If [latex]a|b[/latex] and [latex]a\not{|}c[/latex], then [latex]a\not{|} (bc)[/latex].
- If [latex](ab)|c[/latex], then [latex]a|c[/latex] and [latex]b|c[/latex].
Prove that the following statement is true: "If [latex]a|b[/latex] and [latex]a|(b + c)[/latex], then [latex]a|c[/latex]"
Proof:
If [latex]a|b[/latex], then [latex]am = b[/latex] for some whole number, [latex]m[/latex]. If [latex]a|(b + c)[/latex], then [latex]an = b + c[/latex] for some whole number, [latex]n[/latex]. Keep in mind that since [latex]b[/latex] and [latex]c[/latex] are positive, then [latex](b + c) > b[/latex], which means [latex]n > m[/latex]. We are trying to prove that [latex]a[/latex] is a factor of [latex]c[/latex]. Since [latex]am = b[/latex], we can substitute [latex]am[/latex] for [latex]b[/latex] into the equation [latex]an = b + c[/latex], which means [latex]an = am + c[/latex]. Solving for [latex]c[/latex], this is equivalent to [latex]an – am = c[/latex]. So if [latex]a[/latex] is a factor of [latex]an – am[/latex], then [latex]a[/latex] is a factor of [latex]c[/latex]. Factor: [latex]an – am = a(n – m)[/latex]. This clearly shows [latex]a[/latex] is a factor of [latex]an – am[/latex], which means [latex]a[/latex] is a factor of [latex]c[/latex]. Therefore, the statement "If [latex]a|b[/latex] and [latex]a|(b + c)[/latex], then [latex]a|c[/latex]" is true. (Note: [latex]n – m[/latex] must be a whole number since [latex]n[/latex] and [latex]m[/latex] are whole numbers and [latex]n > m[/latex].)
Divisibility Tests for 2 to 12
All counting numbers can be considered factors of zero. In other words, for all counting numbers, [latex]m[/latex], [latex]m|0[/latex] is always true since there is always some number times [latex]m[/latex] that equals zero, namely zero itself.
Assume [latex]n[/latex] is a positive whole number. The following are divisibility tests to determine what numbers from [latex]2[/latex] to [latex]12[/latex] divide into [latex]n[/latex], or what numbers are factors of [latex]n[/latex]. We divide the numbers from [latex]2[/latex] to [latex]12[/latex] into several families according to their divisibility tests.
Family of 10
The divisibility by [latex]10[/latex] is the most obvious one: if the last digit of a number is [latex]0[/latex], then the number is divisible by [latex]10[/latex], that is, [latex]10[/latex] divides this number. The family of [latex]10[/latex] includes [latex]10[/latex] and its two factors [latex]2[/latex] and [latex]5[/latex]. Similar to the divisibility by [latex]10[/latex], we can observe the last digit of a number to determine if the number is divisible by [latex]2[/latex] or [latex]5[/latex]. For example, if the last digit of a number is an even number, then the number is divisible by [latex]2[/latex]. Similarly, if the last digit of a number is [latex]0[/latex] or [latex]5[/latex], then we know it is divisible by [latex]5[/latex].
Key Takeaway - Divisibility Tests for the Family of 10
The family of [latex]10[/latex] includes three numbers, [latex]10[/latex] and its two factors [latex]2[/latex] and [latex]5[/latex]. To determine if a number [latex]n[/latex] is divisible by one of them, we observe the last digit of [latex]n[/latex]:
- [latex]2|n[/latex] if the last digit of [latex]n[/latex] is even ([latex]0, 2, 4, 6,[/latex] or [latex]8[/latex]).
- [latex]5|n[/latex] if the last digit of [latex]n[/latex] is [latex]0[/latex] or [latex]5[/latex].
- [latex]10|n[/latex] if the last digit of [latex]n[/latex] is [latex]0[/latex].
Let's work on some examples to practice these divisibility tests. We will practice the divisibility test for [latex]2[/latex] in next family, so we'll start with [latex]5[/latex].
Use the divisibility test for [latex]5[/latex] to determine if the following is true or false.
a. [latex]5|527[/latex]
Solution:
This is false because [latex]7[/latex] is the last digit of [latex]527[/latex].
b. [latex]5|25335[/latex]
Solution:
This is true because [latex]5[/latex] is the last digit of [latex]25335[/latex].
c. [latex]5|7620[/latex]
Solution:
This is true because [latex]0[/latex] is the last digit of [latex]7620[/latex].
Below are examples to practice the divisibility test of [latex]10[/latex].
Use the divisibility test for [latex]10[/latex] to determine if the following is true or false.
a. [latex]10|527[/latex]
Solution:
This is false because [latex]7[/latex] is the last digit of [latex]527[/latex].
b. [latex]10|25335[/latex]
Solution:
This is false because [latex]5[/latex] is the last digit of [latex]25335[/latex].
c. [latex]10|7620[/latex]
Solution:
This is true because [latex]0[/latex] is the last digit of [latex]7620[/latex].
Below are more examples for the readers to practice the divisibility tests for [latex]5[/latex] and [latex]10[/latex].
Use the divisibility tests for 5 and 10 to determine if the following is true or false.
a.
b.
c.
d.
e.
Family of Powers of 2
Although [latex]2[/latex] as a factor of [latex]10[/latex] is listed in the family of [latex]10[/latex], it leads a family itself. The divisibility for [latex]2[/latex] can be re-stated as
[latex]2|n[/latex] if [latex]2|[/latex](the last digit of [latex]n[/latex]).
Similarly, the divisibility of a number by [latex]4[/latex] can be determined by only observing its last two digits, and the divisibility of a number by [latex]8[/latex] can be determined by only observing its last three digits.
Key Takeaway - Divisibility Tests for the Family of 2
The family of [latex]2[/latex] includes three numbers: [latex]2[/latex], [latex]4=2^{2}[/latex], and [latex]8=2^3[/latex]. To determine if a number [latex]n[/latex] is divisible by one of them, we observe the last several digits following the divisibility tests below:
- [latex]2|n[/latex] if [latex]2|[/latex](the last digit of [latex]n[/latex]), that is, the last digit of [latex]n[/latex] is even [latex](0, 2, 4, 6,[/latex] or [latex]8)[/latex].
- [latex]4|n[/latex] if [latex]4|[/latex](the number represented by the last two digits of [latex]n[/latex]).
- [latex8|n[/latex] if [latex]8|[/latex](the number represented by the last three digits of [latex]n[/latex]).
Example 5 - Divisibility Test for 2
Use the divisibility test for [latex]2[/latex] to determine if the following is true or false.
a. [latex]2|97[/latex]
Solution:
This is false because the last digit [latex]7[/latex] is not even.
b. [latex]2|356[/latex]
Solution:
This is true because the last digit [latex]6[/latex] is even.
Use the divisibility test for [latex]4[/latex] to determine if the following is true or false.
a. [latex]4|527[/latex]
Solution:
This is false because [latex]4[/latex] not a factor of [latex]27[/latex].
b. [latex]4|25356[/latex]
Solution:
This is true because [latex]4[/latex] is a factor of [latex]56[/latex].
c. [latex]4|624[/latex]
Solution:
This is true because [latex]4[/latex] is a factor of [latex]24[/latex].
Example 7 - Divisibility Test for 8
Use the divisibility test for [latex]8[/latex] to determine if the following is true or false.
a. [latex]8|42527[/latex]
Solution:
This is false because [latex]8[/latex] is not a factor of [latex]527[/latex].
b. [latex]8|25336[/latex]
Solution:
This is true because [latex]8[/latex] is a factor of [latex]336[/latex].
c. [latex]8|7624[/latex]
Solution:
This is true because [latex]8[/latex] is a factor of [latex]624[/latex].
According to the product property of divisibility, it should be clear to you that if a number is divisible by [latex]8[/latex], then it is divisible by both [latex]2[/latex] and [latex]4[/latex]; and if it is divisible by [latex]4[/latex], it is divisible by [latex]2[/latex]. Conversely, if a number is not divisible by [latex]2[/latex], it is not divisible by [latex]4[/latex] or [latex]8[/latex]; and if it is not divisible by [latex]4[/latex], it is not divisible by [latex]8[/latex].
Use the divisibility tests for [latex]2, 4[/latex] and [latex]8[/latex] to determine if the following is true or false. Support your answer with a reason using the appropriate divisibility test.
a. [latex]2|9712[/latex]
Solution
This is true because the last digit [latex]2[/latex] is even.
b. [latex]2|5643[/latex]
Solution
This is false because the last digit [latex]3[/latex] is not even.
c. [latex]4|5690[/latex]
Solution
This is false because [latex]4[/latex] is not a factor of [latex]90[/latex].
d. [latex]4|63868[/latex]
Solution
This is true because [latex]4[/latex] is a factor of [latex]68[/latex].
e. [latex]4|854100[/latex]
Solution
This is true because [latex]4[/latex] is a factor of [latex]00[/latex].
f. [latex]8|12345248[/latex]
Solution
This is true because [latex]8[/latex] is a factor of [latex]248[/latex].
g. [latex]8|54094422[/latex]
Solution
This is false because [latex]8[/latex] is not a factor of [latex]422[/latex].
Further exploration: Can you develop a divisibility test for [latex]25[/latex]?
Family of 3 and 9
The divisibility tests for members in this family are about the digital roots we discussed in the last section. Recall that the digital root of a number is the remainder obtained when a number is divided by [latex]9[/latex], and that the digital root of a number can be calculated by adding its digits and casting out [latex]9[/latex]s. Therefore, "the digital root of a number is [latex]0[/latex]" means that [latex]9[/latex] divides this number. Similarly, the divisibility of a number by [latex]3[/latex] can be determined by the divisibility of its digital root by [latex]3[/latex].
Key Takeaways - Divisibility Tests for the Family of 3 and 9
The divisibility tests for the family of [latex]3[/latex] and [latex]9[/latex], using the digit root of a number, are stated below:
- [latex]3|n[/latex] if [latex]3|[/latex](the digital root of [latex]n[/latex]). That is, [latex]3|n[/latex] if the digital root of [latex]n[/latex] is [latex]0, 3[/latex] or [latex]6[/latex].
- [latex]9|n[/latex] if [latex]9|[/latex](the digital root of [latex]n[/latex]). That is, [latex]9|n[/latex] if the digital root of [latex]n[/latex] equals [latex]0[/latex].
Example 8 helps us to practice the divisibility test for [latex]3[/latex].
Use the divisibility test for [latex]3[/latex] to determine if the following is true or false.
a. [latex]3|97[/latex]
Solution:
This is false because [latex]3[/latex] does not divide [latex]7[/latex], which is the digital root of [latex]97[/latex].
b. [latex]3|356[/latex]
Solution:
This is false because [latex]3[/latex] does not divide [latex]5[/latex], which is the digital root of [latex]356[/latex].
c. [latex]3|738[/latex]
Solution:
This is true because [latex]3[/latex] divides [latex]0[/latex], where [latex]0[/latex] is the digital root of [latex]738[/latex].
By doing the examples above, we can see the advantage of using digital root to determine the divisibility of a number by [latex]3[/latex], especially when the number is very large. For example, to determine if [latex]738[/latex] is divisible by [latex]3[/latex], we don't need to do the division of [latex]738\div3[/latex] to examine if its remainder is zero or not; instead, we only need to add the digits and examine the divisibility of the digital root, which is much smaller. This is one of the most important mathematical ideas that helps us turn a hard problem into a much easier one. Additionally, as we have practiced in the previous section, we are free from the use of the calculator even for a number with 6 digits or more! In the exercise below, you will feel more empowered by doing the easy math of calculating the digital root to determine the divisibility.
Use the divisibility test for [latex]3[/latex] to determine if the following is true or false. Support your answer with a reason using the divisibility test for [latex]3[/latex].
a. [latex]3|9750[/latex]
Solution
This is true because [latex]3[/latex] divides [latex]3[/latex], where [latex]3[/latex] is the digital root of [latex]9750[/latex].
b. [latex]3|5645[/latex]
Solution
This is false because [latex]3[/latex] does not divide [latex]2[/latex], which is the digital root of [latex]5645[/latex].
c. [latex]3|5696[/latex]
Solution
This is false because [latex]3[/latex] does not divide [latex]8[/latex], which is the digital root of [latex]5696[/latex].
d. [latex]3|63860[/latex]
Solution
This is false because [latex]3[/latex] does not divide [latex]5[/latex], which is the digital root of [latex]36860[/latex].
e. [latex]3|854115[/latex]
Solution
This is true because [latex]3[/latex] divides [latex]6[/latex], where [latex]6[/latex] is the digital root of [latex]3854115[/latex].
Example 9 is for us to practice the divisibility test for [latex]9[/latex]. Again, reflect on what you would do if you hadn't learned the concept of digital root, and how much easier when we just need to work on the digital root of each number.
Use the divisibility test for [latex]9[/latex] to determine if the following is true or false.
a. [latex]9|627[/latex]
Solution:
This is false because [latex]9[/latex] does not divide [latex]6[/latex], which is the digital root of [latex]627[/latex].
b. [latex]9|25334[/latex]
Solution:
This is false because [latex]9[/latex] does not divide [latex]8[/latex], which is the digital root of [latex]25334[/latex].
c. [latex]9|7533[/latex]
Solution:
This is true because the digital root of [latex]7533[/latex] is [latex]9 \rightarrow 0[/latex].
Below are some big numbers for you to practice. Do you feel good when you can handle this kind of big numbers that may be scary for others?
Use the divisibility test for [latex]9[/latex] to determine if the following is true or false. Support your answer with a reason using the divisibility test for [latex]9[/latex]. Show work.
a. [latex]9|9753[/latex]
Solution
This is false because [latex]9[/latex] does not divide [latex]6[/latex], which is the digital root of [latex]9753[/latex].
b. [latex]9|5646[/latex]
Solution
This is false because [latex]9[/latex] does not divide [latex]3[/latex], which is the digital root of [latex]5646[/latex].
c. [latex]9|5697[/latex]
Solution
This is true because the digital root of [latex]5697[/latex] is [latex]9 \rightarrow 0[/latex].
d. [latex]9|63576[/latex]
Solution
This is true because the digital root of [latex]63576[/latex] is [latex]9 \rightarrow 0[/latex].
e. [latex]9|854103[/latex]
Solution
This is false because [latex]9[/latex] does not divide [latex]3[/latex], which is the digital root of [latex]854103[/latex].
Family of 6 and 12
Both [latex]6[/latex] and [latex]12[/latex] have multiple factors other than [latex]1[/latex] and themselves. We can call this family "multi-factor family". For [latex]6[/latex], we can use divisibility tests for [latex]2[/latex] and [latex]3[/latex] to determine if a number is divisible by [latex]6[/latex]. For [latex]12[/latex] as product of [latex]3[/latex] and [latex]4[/latex], we use the tests for [latex]3[/latex] and [latex]4[/latex].
Note: While [latex]12[/latex] is also the product of [latex]2[/latex] and [latex]6[/latex], we don't use these tests to determine [latex]12[/latex]'s divisibility since [latex]6[/latex] also relies on other divisibility tests.
Key Takeaway - Divisibility Tests for the Family of 6 and 12
This family includes two numbers [latex]6[/latex] and [latex]12[/latex], and the divisibility of a number by them can use the tests for others that we've learned:
- [latex]6|n[/latex] if [latex]2|n[/latex] AND [latex]3|n[/latex]. (Think of [latex]6[/latex] as [latex]2\times 3[/latex])
- [latex]12|n[/latex] if [latex]3|n[/latex] AND [latex]4|n[/latex]. (Think of [latex]12[/latex] as [latex]3\times 4[/latex])
Important Note: A number is divisible by [latex]6[/latex] only if it passes the divisibility test for both [latex]2[/latex] and [latex]3[/latex]. If a number doesn't pass one of the tests, then it is not divisible by [latex]6[/latex]. Similarly, to show a number is divisible by [latex]12[/latex], we must show it passes both of the tests for [latex]3[/latex] and [latex]4[/latex]. On the contrary, if it doesn't pass one of the tests for [latex]3[/latex] or [latex]4[/latex], we can conclude that it is not divisible by [latex]12[/latex].
Use the divisibility test for [latex]6[/latex] to determine if the following is true or false.
a. [latex]6|627[/latex]
Solution:
This is false because [latex]2[/latex] does not divide [latex]7[/latex] (the last digit, which is not even).
b. [latex]6|25334[/latex]
Solution:
This is false because [latex]3[/latex] does not divide [latex]25334[/latex], since [latex]3[/latex] does not divide the digital root [latex]8[/latex].
c. [latex]6|7620[/latex]
Solution:
This is true because [latex]2[/latex] divides [latex]7620[/latex] (since the last digit, [latex]0[/latex], is even) AND [latex]3[/latex] divides [latex]7620[/latex] (since [latex]3[/latex] divides the digital root [latex]6[/latex]).
Use the divisibility test for [latex]6[/latex] to determine if the following is true or false. Support your answer with a reason using the divisibility test for [latex]6[/latex].
a. [latex]6|9753[/latex]
Solution
This is false because [latex]2[/latex] does not divide [latex]3[/latex] (the last digit, which is not even).
b. [latex]6|5645[/latex]
Solution
This is false because [latex]2[/latex] does not divide [latex]5[/latex] (the last digit, which is not even).
c. [latex]6|5696[/latex]
Solution
This is false because [latex]3[/latex] does not divide [latex]5696[/latex], since [latex]3[/latex] does not divide the digital root [latex]8[/latex].
d. [latex]6|63876[/latex]
Solution
This is true because [latex]2[/latex] divides [latex]63876[/latex] (since the last digit, [latex]6[/latex], is even) AND [latex]3[/latex] divides [latex]63876[/latex] (since [latex]3[/latex] divides the digital root [latex]3[/latex]).
e. [latex]6|854103[/latex]
Solution
This is false because [latex]2[/latex] does not divide [latex]3[/latex] (the last digit, which is not even).
Use the divisibility test for [latex]12[/latex] to determine if the following is true or false.
a. [latex]12|623[/latex]
Solution:
This is false because [latex]4[/latex] does not divide the last two digits [latex]23[/latex].
b. [latex]12|2234[/latex]
Solution:
This is false because [latex]3[/latex] does not divide [latex]2234[/latex], since [latex]3[/latex] does not divide the digital root [latex]2[/latex].
c. [latex]12|7620[/latex]
Solution:
This is true because [latex]4[/latex] divides the last two digits [latex]20[/latex] AND [latex]3[/latex] divides the digital root [latex]6[/latex].
Use the divisibility test for [latex]12[/latex] to determine if the following is true or false. Support your answer with a reason using the divisibility test for [latex]12[/latex].
a. [latex]12|8514[/latex]
Solution
This is false because [latex]4[/latex] does not divide the last two digits [latex]14[/latex].
b. [latex]12|9756[/latex]
Solution
This is true because [latex]4[/latex] divides the last two digits [latex]56[/latex] AND [latex]3[/latex] divides the digital root [latex]9 \rightarrow 0[/latex].
c. [latex]12|5680[/latex]
Solution
This is false because [latex]3[/latex] does not divide [latex]5680[/latex], since [latex]3[/latex] does not divide the digital root [latex]1[/latex].
d. [latex]12|13870[/latex]
Solution
This is false because [latex]4[/latex] does not divide the last two digits [latex]70[/latex].
e. [latex]12|309756[/latex]
Solution
This is true because [latex]4[/latex] divides the last two digits [latex]56[/latex] AND [latex]3[/latex] divides the digital root [latex]3[/latex].
Further exploration: Can you develop a divisibility test for [latex]15[/latex]?
Family of 7 and 11
[latex]7[/latex] and [latex]11[/latex] do not share a similar test; they are put into the same family because of the uniqueness of their divisibility tests.
Divisibility Test for 7
The divisibility of a number by [latex]7[/latex] can be tested by following the steps below:
Step 1: Cross off the one's digit of the number to get a number with one less place value.
Step 2: Double the one's digit you crossed off and subtract from the new number obtained with the one's digit missing.
Step 3: If [latex]7[/latex] divides the number you get after subtracting, it divides the original number. Otherwise, it doesn't. If you aren't sure, repeat the procedure on the new number by going back to step 1.
Use the divisibility test for [latex]7[/latex] to determine if the following is true or false. The way you would show the steps using the numbers is shown to the right of the explanation.
a. [latex]7|91[/latex]
Solution:
Cross off the [latex]1[/latex], double it ([latex]2[/latex]), and subtract from what is left ([latex]9[/latex]). The answer is [latex]7[/latex] since [latex]9 – 2 = 7[/latex]. This means that [latex]7|7[/latex] so [latex]7|91[/latex] is true. The work is shown below:
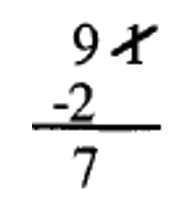
b. [latex]7|96[/latex]
Solution:
Cross off the [latex]6[/latex], double it ([latex]12[/latex]), and subtract from what is left ([latex]9[/latex]). When you subtract, ignore the sign, so just do [latex]12 – 9 = 3[/latex]. Since [latex]7[/latex] does not divide [latex]3[/latex] then [latex]7|96[/latex] is false. The work is shown below.
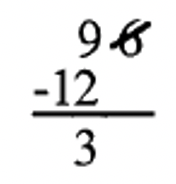
c. [latex]7|638[/latex]
Solution:
Cross off the [latex]8[/latex], double it ([latex]16[/latex]) and subtract from what is left ([latex]63[/latex]). The answer is [latex]47[/latex] since [latex]63 – 16 = 47[/latex]. [latex]7[/latex] does not divide [latex]47[/latex], so [latex]7|638[/latex] is false. The work is shown below to the left.
If you weren't sure whether or not [latex]7[/latex] divided [latex]47[/latex], you can take it a step further; this is shown to the right.
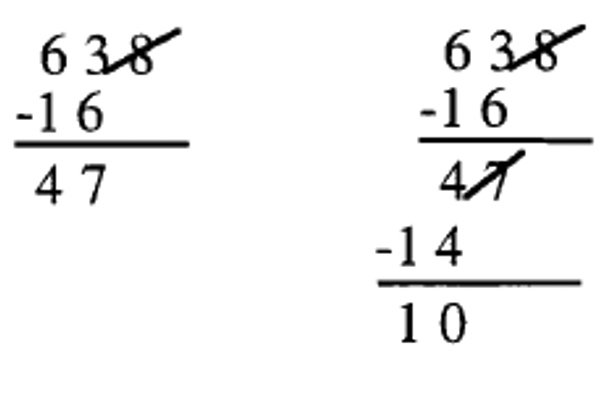
d. [latex]7|4564[/latex]
Solution:
Cross off the [latex]4[/latex], double it ([latex]8[/latex]) and subtract from what is left ([latex]456[/latex]). The answer is [latex]448[/latex] because [latex]456 – 8 = 456[/latex]. Since [latex]456[/latex] is such a large answer, we may need to repeat the process. Cross off the [latex]8[/latex], double it ([latex]16[/latex]) and subtract from what is left ([latex]44[/latex]). The answer is [latex]28[/latex] because [latex]44 – 16 = 28[/latex]. Since [latex]7|28[/latex], then [latex]7|4564[/latex] is true. The work is shown below.
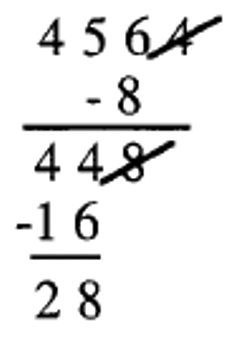
e. [latex]7|56161[/latex]
Solution:
Cross off the [latex]1[/latex], double it ([latex]2[/latex]) and subtract from what is left ([latex]5616 – 2 = 5614[/latex]). Repeat the process. Cross off the [latex]4[/latex], double it ([latex]8[/latex]) and subtract from what is left ([latex]561 – 8 = 553[/latex]). We still have a large number to work with, so repeat the process again. Cross off the [latex]3[/latex], double it ([latex]6[/latex]) and subtract from what is left ([latex]55 – 6 = 49[/latex]). Since [latex]7|49[/latex], then [latex]7|56161[/latex] is true. The work is shown below.
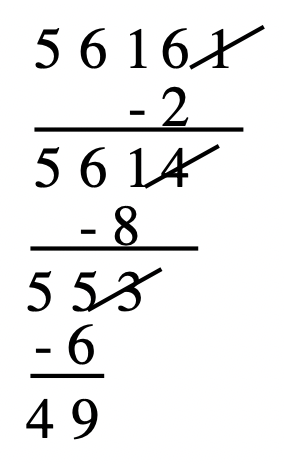
Use the divisibility test for [latex]7[/latex] to determine if the following is true or false. Support your answer with a reason using the divisibility test for [latex]7[/latex]. Show work.
a. [latex]7|833[/latex]
Solution
Cross off the [latex]3[/latex], double it ([latex]6[/latex]), and subtract from what is left ([latex]83[/latex]). The answer is [latex]77[/latex] since [latex]83 - 6 = 77[/latex]. This means that [latex]7|77[/latex] so [latex]7|833[/latex] is true.
b. [latex]7|5645[/latex]
Solution
Cross off the [latex]5[/latex], double it ([latex]10[/latex]) and subtract from what is left ([latex]564[/latex]). The answer is [latex]554[/latex] since [latex]564 – 10 = 554[/latex]. Repeat the process again. Cross off the [latex]4[/latex], double it ([latex]8[/latex]) and subtract from what is left ([latex]55[/latex]). The answer is [latex]47[/latex] since [latex]55 – 8 = 47[/latex]. Now [latex]7[/latex] does not divide [latex]47[/latex], so [latex]7|5645[/latex] is false.
c. [latex]7|4795[/latex]
Solution
Cross off the [latex]5[/latex], double it ([latex]10[/latex]) and subtract from what is left ([latex]479[/latex]). The answer is [latex]469[/latex] since [latex]479 – 10 = 469[/latex]. Repeat the process again. Cross off the [latex]9[/latex], double it ([latex]18[/latex]) and subtract from what is left ([latex]46[/latex]). The answer is [latex]28[/latex] since [latex]46 – 18 = 28[/latex]. Now [latex]7[/latex] divides [latex]28[/latex], so [latex]7|4795[/latex] is true.
d. [latex]7|14763[/latex]
Solution
Cross off the [latex]3[/latex], double it ([latex]6[/latex]) and subtract from what is left ([latex]1476[/latex]). The answer is [latex]1470[/latex] since [latex]1476 – 6 = 1470[/latex]. Repeat the process again. Cross off the [latex]0[/latex], double it ([latex]0[/latex]) and subtract from what is left ([latex]147[/latex]). The answer is [latex]147[/latex] since [latex]147 – 0 = 147[/latex]. Repeat the process again. Cross off the [latex]7[/latex], double it ([latex]14[/latex]) and subtract from what is left ([latex]14[/latex]). The answer is [latex]0[/latex] since [latex]14 – 14 = 0[/latex]. Now [latex]7[/latex] divides [latex]0[/latex], so [latex]7|14763[/latex] is true.
Divisibility Test for 11
Next, we work on the divisibility test for [latex]11[/latex]. It can be described as below:
[latex]11|n[/latex] if the difference between the sum of the digits in the places that are even powers of [latex]10[/latex] and the sum of the digits in the places that are odd powers of [latex]10[/latex] is divisible by [latex]11[/latex].
This test is more confusing to describe than to do. What you do is add up every other digit. Then, add up the ones you skipped. Then, subtract these two numbers and see if [latex]11[/latex] divides this number.
Use the divisibility test for [latex]11[/latex] to determine if the following is true or false.
a. [latex]11|4365[/latex]
Solution:
Add [latex]3 + 5 = 8[/latex] (the digits in the even powers of [latex]10[/latex]).
Add [latex]4 + 6 = 10[/latex] (the digits in the odd powers of [latex]10[/latex]).
Subtract [latex]10 – 8 = 2[/latex].
Since [latex]11[/latex] doesn't divide [latex]2[/latex], then [latex]11[/latex] doesn't divide [latex]4365[/latex]. Therefore, [latex]11|4365[/latex] is false.
b. [latex]11|540879216[/latex]
Solution:
Add [latex]5 + 0 + 7 + 2 + 6 = 20[/latex] (the digits in the even powers of [latex]10[/latex]).
Add [latex]4 + 8 + 9 + 1 = 22[/latex] (the digits in the odd powers of [latex]10[/latex].)
Subtract [latex]22 – 20 = 2[/latex].
Since [latex]11[/latex] doesn't divide [latex]2[/latex], then [latex]11|540879216[/latex] is false.
c. [latex]11|542879216[/latex]
Solution:
Add [latex]5 + 2 + 7 + 2 + 6 = 22[/latex] (the digits in the even powers of [latex]10[/latex]).
Add [latex]4 + 8 + 9 + 1 = 22[/latex] (the digits in the odd powers of [latex]10[/latex].)
Subtract [latex]22 – 22 = 0[/latex].
Since [latex]11[/latex] does divide [latex]0[/latex], then [latex]11|542879216[/latex] is true.
d. [latex]11|4052631[/latex]
Solution:
Add [latex]4 + 5 + 6 + 1 = 16[/latex] (the digits in the even powers of [latex]10[/latex]).
Add [latex]0 + 2 + 3 = 5[/latex] (the digits in the odd powers of [latex]10[/latex].)
Subtract [latex]16 – 5 = 11[/latex].
Since [latex]11[/latex] does divide itself, [latex]11[/latex], then [latex]11|4052631[/latex] is true.
Use the divisibility test for [latex]11[/latex] to determine if the following is true or false. Support your answer with a reason using the divisibility test for [latex]11[/latex]. Show work.
a. [latex]11|9053[/latex]
Solution
Add [latex]0 + 3 = 3[/latex] (the digits in the even powers of [latex]10[/latex]).
Add [latex]9 + 5 = 14[/latex] (the digits in the odd powers of [latex]10[/latex].)
Subtract [latex]14 – 3 = 11[/latex].
Since [latex]11[/latex] does divide [latex]11[/latex], then [latex]11|9053[/latex] is true.
b. [latex]11|63920876[/latex]
Solution
Add [latex]3 + 2 + 8 + 6 = 19[/latex] (the digits in the even powers of [latex]10[/latex]).
Add [latex]6 + 9 + 0 + 7 = 22[/latex] (the digits in the odd powers of [latex]10[/latex].)
Subtract [latex]22 – 19 = 3[/latex].
Since [latex]11[/latex] doesn't divide [latex]3[/latex], then [latex]11|63920876[/latex] is false.
c. [latex]11|568696[/latex]
Solution
Add [latex]6 + 6 + 6 = 18[/latex] (the digits in the even powers of [latex]10[/latex]).
Add [latex]5 + 8 + 9 = 22[/latex] (the digits in the odd powers of [latex]10[/latex].)
Subtract [latex]22 – 18 = 4[/latex].
Since [latex]11[/latex] doesn't divide [latex]4[/latex], then [latex]11|568696[/latex] is false.
d. [latex]11|513645[/latex]
Solution
Add [latex]1 + 6 + 5 = 12[/latex] (the digits in the even powers of [latex]10[/latex]).
Add [latex]5 + 3 + 4 = 12[/latex] (the digits in the odd powers of [latex]10[/latex].)
Subtract [latex]12 – 12 = 0[/latex].
Since [latex]11[/latex] does divide [latex]0[/latex], then [latex]11|513645[/latex] is true.
e. [latex]11|803003808[/latex]
Solution
Add [latex]8 + 3 + 0 + 8 + 8 = 27[/latex] (the digits in the even powers of [latex]10[/latex]).
Add [latex]0 + 0 + 3 + 0 = 3[/latex] (the digits in the odd powers of [latex]10[/latex].)
Subtract [latex]27 – 3 = 24[/latex].
Since [latex]11[/latex] doesn't divide [latex]24[/latex], then [latex]11|803003808[/latex] is false.
Listed below are the divisibility tests that you should know. It's important to realize that each of the tests only works for the number specified. In other words, you can't use the divisibility test for [latex]3[/latex] to determine if [latex]7[/latex] divides a number. The divisibility test for [latex]7[/latex] has nothing to do with digital roots!
Divisibility Test for [latex]2[/latex]: [latex]2|n[/latex] if the last digit of [latex]n[/latex] is even ([latex]0, 2, 4, 6,[/latex] or [latex]8[/latex]).
Divisibility Test for [latex]3[/latex]: [latex]3|n[/latex] if [latex]3|[/latex](the digital root of [latex]n[/latex]); OR [latex]3|n[/latex] if the digital root of [latex]n[/latex] is [latex]0, 3[/latex] or [latex]6[/latex].
Divisibility Test for [latex]4[/latex]: [latex]4|n[/latex] if [latex]4|[/latex](the number represented by the last two digits of [latex]n[/latex]).
Divisibility Test for [latex]5[/latex]: [latex]5|n[/latex] if the last digit of [latex]n[/latex] is [latex]0[/latex] or [latex]5[/latex].
Divisibility Test for [latex]6[/latex]: [latex]6|n[/latex] if [latex]2|n[/latex] AND [latex]3|n[/latex]. (Think of [latex]6[/latex] as [latex]2 \times 3[/latex])
Divisibility Test for [latex]7[/latex]: The steps of this test are described below.
- Step 1: Cross off the one's digit of the number to get a number with one less place value.
- Step 2: Double the one's digit you crossed off and subtract from the new number without the one's digit.
- Step 3: If [latex]7[/latex] divides the number you get after subtracting, it divides the original number. Otherwise, it doesn't. If you aren't sure, repeat the procedure on the new number by going back to step 1.
Divisibility Test for [latex]8[/latex]: [latex]8|n[/latex] if [latex]8|[/latex](the number represented by the last three digits of [latex]n[/latex]).
Divisibility Test for [latex]9[/latex]: [latex]9|n[/latex] if [latex]9[/latex]|(the digital root of [latex]n[/latex]); OR [latex]9|n[/latex] if the digital root of [latex]n[/latex] is zero.
Divisibility Test for [latex]10[/latex]: [latex]10|n[/latex] if the last digit of [latex]n[/latex] is [latex]0[/latex].
Divisibility Test for [latex]11[/latex]: [latex]11|n[/latex] if the difference between the sum of the digits in the places that are even powers of [latex]10[/latex] and the sum of the digits in the places that are odd powers of [latex]10[/latex] is divisible by [latex]11[/latex].
Divisibility Test for [latex]12[/latex]: [latex]12|n[/latex] if [latex]3|n[/latex] AND [latex]4|n[/latex].
Further exploration: Can you develop divisibility rules for [latex]14[/latex], [latex]15[/latex], and [latex]18[/latex]?
