16 Other Base Systems
You will need: Arcade Prize Tokens (Material Card 3), Calculator
If you have ever learned another language, one of the unexpected consequences is a greater understanding of the grammar for your native language. Learning other number bases will have the same effect on your understanding of base ten! In this section, we will look at how to convert (i.e. translate) between other number bases and your "native" language of base ten. Unless the standards change somewhere down the road, your future students will only need to work in base ten, but you will be a better teacher for having looked at other number bases.
Exploration Activity
Let's revisit the High Five Arcade from the previous section. Recall that you can earn “prize tokens” in the values of one, five, twenty-five, one hundred twenty-five, and six hundred twenty-five prize points. After a long day of playing games you have amassed
- 3 six hundred twenty-five point tokens;
- 4 one hundred twenty-five point tokens;
- 0 twenty-five point tokens;
- 1 five-point tokens;
- 3 one-point tokens.
How many total points have you earned?
Converting from Other Number Bases to Base Ten
Think about the exploration activity you just completed. You just converted [latex]34013_{\text{five}}[/latex] into a base ten numeral! Because base ten is our native language, we naturally convert values into base ten. The process just requires an understanding of place value.
Example
Convert the following numerals to the equivalent base ten numeral.
a. [latex]34013_{\text{five}}[/latex]
Solution: The first step is to list our place values for the number we are given. Since we are in base five, the place-values will be powers of 5.
Place Value |
625's |
125's |
25's |
5's |
1's |
Digit |
3 | 4 | 0 | 1 | 3 |
Writing the numeral in expanded form gives
[latex](3\times 625)+(4\times 125)+(0\times 25)+(1\times 5)+(3\times 1)[/latex].
Performing the written products and sums puts the number into our native language of base ten.
Answer: [latex]2383[/latex]
b. [latex]3202_{\text{four}}[/latex]
Solution: Writing the expanded form of our base four numeral gives
[latex](3\times 4^3)+(2\times 4^2)+(0\times 4)+(2\times 1)[/latex]
[latex](3\times 64)+(2\times 16)+(0\times 4)+(2\times 1)[/latex]
Answer: [latex]226[/latex]
Exercise 1
Convert the following numerals to the equivalent base ten numeral.
a. [latex]5542_{\text{six}}[/latex]
b. [latex]1203_{\text{five}}[/latex]
c. [latex]110110_{\text{two}}[/latex]
d. [latex]3\text{TE}4_{\text{twelve}}[/latex]
Notice how when you write the numeral in expanded form, before you even add up the values, it gives you a better intuition about the number. It is hard to imagine the value of [latex]102211_{\text{three}}[/latex], but
[latex](1\times 243)+(0\times 81)+(2\times 27)+(2\times 9)+(1\times 3)+(1\times 1)[/latex]
gives you an idea of the size of the number.
Exploration Activity
You are back at the High Five Arcade playing your favorite game. Recall that you can earn “prize tokens” in the values of one, five, twenty-five, one hundred twenty-five, and six hundred twenty-five prize points. You get a new high score and the machine awards you 2304 prize points. Use your cut out Arcade Prize Tokens and a calculator to figure out how many of each token type you get if the machine gives you the least number of tokens possible.
Converting from Base Ten to Other Number Bases
Because we think in base ten, going from base ten to other bases requires a different process. Think about how you solved the exploration activity. You probably started with the 625 point pieces and worked your way down. That is exactly how to convert from base ten to a different number base: start with your base ten numeral and split it into pieces based on the desired place values, starting with the largest place value smaller than your number.
Example
Convert the following base ten numerals to the equivalent numeral in the given base.
a. 1000 to Base Three
First, we need to list our place values for base three by listing powers of 3.
2187 729 243 81 27 9 3 1
Since 2187 is larger than our given number of 1000, we can stop at the 729 place.
How many 729's are there in 1000? There is 1.
Place Value |
729 |
243 |
81 |
27 |
9 |
3 |
1 |
Digit |
1 |
Now, we need to subtract the value we have used [latex](1\times 729)[/latex] from 1000.
1000 - 729 = 271
Our next largest place value is 243. How many 243's are there in 271? Again, there is only one.
Place Value |
729 |
243 |
81 |
27 |
9 |
3 |
1 |
Digit |
1 | 1 |
Subtracting [latex](1\times 243)[/latex] from 271 gives
271 - 243 = 28.
We still have 28 left to distribute. Our next place value is 81 and we cannot fit any 81's into 28.
Place Value |
729 |
243 |
81 |
27 |
9 |
3 |
1 |
Digit |
1 | 1 | 0 |
Now we can fit one 27 into 28.
Place Value |
729 |
243 |
81 |
27 |
9 |
3 |
1 |
Digit |
1 | 1 | 0 | 1 |
This means we have used 27 of our 28.
28 - 27 = 1
Now we only have 1 left to distribute. That gives us zero 9's, zero 3's, and one 1.
Place Value |
729 |
243 |
81 |
27 |
9 |
3 |
1 |
Digit |
1 | 1 | 0 | 1 | 0 | 0 | 1 |
Answer: [latex]1101001_{\text{three}}[/latex]
b. 1000 to Base Twelve
Our base twelve place values are
1728 144 12 1
Start with the largest place value smaller than 1000 (which is 144) and start grouping. Testing on the calculator gives 144[latex]\times[/latex]7 = 1008, so there are six 144's in 1000. Since 6 [latex]\times[/latex]144=864, we have
1000 - 864 = 136.
How many 12's are there in 136? 12[latex]\times[/latex]11 = 132, so there are eleven 12's in 136.
136 - 132 = 4
The remaining 4 means we have four 1's.
Place Value |
144 |
12 |
1 |
Digit |
6 | E | 4 |
Answer: [latex]6\text{E}4_{\text{twelve}}[/latex]
Exercise 2
Convert the following base ten numerals to the equivalent numeral in the given base.
a. 3047 to Base Eight
b. 99 to Base Four
c. 1121 to Base Eleven
d. 847 to Base Two
Alternate Approach to Converting from Base Ten to Other Number Bases
There is another method to convert from other number bases to base ten. This method takes advantage of the fact that our place values are all powers of the same number. It is quick and easy if you use it correctly.
Caution: Be wary of "quick and easy" algorithms. If you do not understand what you are doing and why it works, you are much more likely to mess up the steps!
To understand our algorithm, let's start in our native system of base ten. Consider the numeral 36248. Notice that all of the place values are divisible by 10, except for the ones place. So, if we divide by 10, everything will divide perfectly except for the ones place. That means the remainder of 36248[latex]\div[/latex]10 is the digit in the ones place.
[latex]36248\div 10=3624[/latex] rem. [latex]8\;\leftarrow[/latex] ones place
Now we have dropped everything down one place value to 3624. If we divide by 10, again, everything will divide evenly except for that now ones, used to be tens place.
[latex]3624\div 10=362[/latex] rem. [latex]4\;\leftarrow[/latex] tens place
This works because we have now divided the original 36248 by 100 overall. Every place value is divisible by 100 except for the tens and ones places. That's why those were the only ones to appear as remainders. We can continue this process through all of the place values. Each time we divide by 10, our remainder is what was in the next place value.
[latex]362\div 10=36[/latex] rem. [latex]2\;\leftarrow[/latex] hundreds place
[latex]36\div 10=3[/latex] rem. [latex]6\;\leftarrow[/latex] thousands place
[latex]3\div 10=0[/latex] rem. [latex]3\;\leftarrow[/latex] ten thousands place
This is a bit silly in base ten, because we basically just converted from base ten to base ten. That is a bit ridiculous. Let's look at how it works in another number base.
Example
Convert the 827464 to a base thirteen numeral.
Solution: Our place values will all be divisible by 13 except for the ones place, so let's divide by 13 and see what our remainder is.
[latex]827464\div 13=63651[/latex] rem. [latex]1\;\leftarrow[/latex] ones place
Now if we divide by 13 again, the 13's place will be our remainder (because it only has one 13 as a factor, not two of them).
[latex]63651\div 13=4896[/latex] rem. [latex]3\;\leftarrow[/latex] thirteens place
And we can continue the process. Each time we divide by 13, we are moving up one more place value in our number.
[latex]4896\div 13=376[/latex] rem. [latex]8\;\leftarrow[/latex] one hundred sixty nines place
[latex]376\div 13=28[/latex] rem. [latex]12\;\leftarrow[/latex] 2197's place
[latex]28\div 13=2[/latex] rem. [latex]2\;\leftarrow[/latex] 28561's place
[latex]2\div 13=0[/latex] rem. [latex]2\;\leftarrow[/latex] 371293's place
The 2197's place has twelve items in it. Recall that our symbol for twelve is [latex]\text{W}[/latex].
Answer: [latex]22\text{W}831_{\text{thirteen}}[/latex]
Exercise 3
For each of the following base ten numerals, convert it to its equivalent numeral in the given base using the method of remainders.
a. 8364 to Base Seven
b. 527 to Base Four
c. 399 to Base Six
d. 10000 to Base Twelve
Bringing it Back to the Classroom
To end this section, you will be given a variety of classroom scenarios. All of the numerals are in base ten unless stated otherwise. Now that you understand place value and have tools to explain it, see how well you can help these students. Start by identifying what the student's misconception is and then correct their thinking.
Sample solutions are given, but these are not the only way to explain what is going on!
Scenario 1
Melody is having a hard time understanding why 10000 is larger than 999 since 9 is a lot more than 1 and 0. What would you tell her?
Solution
Misconception: Melody does not understand that the value changes depending on what place a digit is in.
Conversation: Melody, let's look at the block representations for 9 and 100. The blocks look like:
Looking at the blocks, which one is bigger? Why was the 9 not enough to make it the bigger number? Because the 9 unit pieces are so much smaller than the one flat.
Now let's look at 100 and 90. Which one is bigger?

Again, the 9 long pieces are still smaller than the one flat.
What about 100 and 900?

Now, the 9 pieces are the same size as the one piece, so 900 is larger than 100.
If we have the numbers 10000 and 90000, which is larger? Because 9 is bigger than 1 AND they are in the same place value, 90000 is larger.
Let's look back at the original problem: 10000 and 999. The nines are in much smaller place values, so 999 is actually smaller than 10000.
Scenario 2
Jeremy is confused about why the number after 99 is 100. Use base ten blocks to explain it to him.
Solution
Misconception: Jeremy doesn't understand how adding one to 9 triggers a trade, and, in this case, a cascade of trades.
Conversation: First, let's look at why we count 8, 9, 10. If we have 8 units, and add one more unit, that makes nine units.
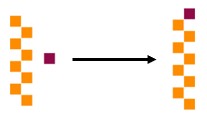
Now, if we add one more unit to our nine units, we have ten units. But, ten units is the same as a long, so we must trade all ten units for one long.
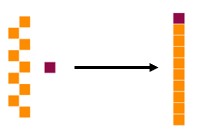
That is why we write 10: it represents 1 long and zero units.
Consider 99. If we add one more unit, we get the number after 99. But we already have 9 units, so adding one more, gives us ten units. These ten units must be traded for a long.
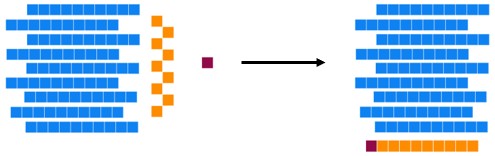
But now, look at the longs. We have ten longs, which is the same as a flat. So, all ten of the longs must be traded for a flat.
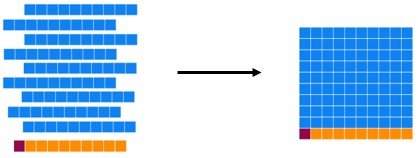
This is why the number after 99 is 100. It is one flat, zero longs, and zero units.
Scenario 3
Zoe says that 2003 and 203 are the same number because zero has no value. How can you help her?
Solution
Misconception: Zoe doesn't understand that zero can act as a place holder to help determine the place value of the digit around it. She is confusing its value with its purpose in a multi-digit numeral.
Conversation: Let's review our place values. In 2003, the 3 is in the ones place and the 2 is in the thousands place (because we have zeros in the tens and hundreds places). This means we have 2 one thousand pieces and 3 unit pieces. What about 203? The 3 is in the ones place, so we have 3 unit pieces, but we only have one place value between the 2 and the 3. So, the 2 is in the hundreds place (because the zero is in the tens place). This means we have 2 on hundred pieces and 3 unit pieces. Are the two numbers the same? Do they have the same value when you put the pieces together? No, they don't. You are correct that zero has no value, but it does make a difference in the number, because the zeros are clarifying what place values the other digits are in.
Scenario 4
Xavier says the following picture represents the number 9113. Where is his mistake? Use blocks and the idea of place value to help him.

Solution
Misconception: Xavier understands which block type represents which place value, but doesn't recognize when to trade blocks. He is just counting how many blocks there are of each type.
Conversation: Xavier, what number does this arrangement of blocks represent?
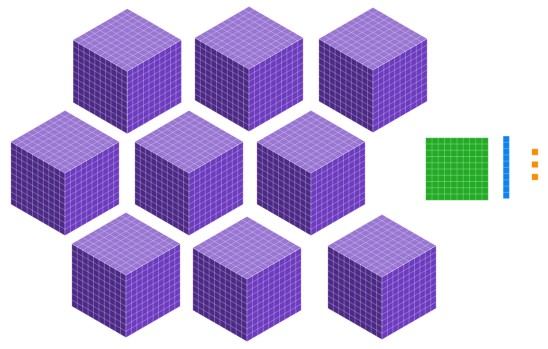
It is 9113, but that is different from the picture you had. This new one shows 9 one thousands, 1 one hundred, 1 ten, and 3 ones. This is very different from the other set up! Let's look back at the original arrangement of blocks. The problem is with the longs. How many longs are there? But how do we represent the number eleven? When we write 11 we are saying "one group of ten and one one." So, we need to make a group of ten. What do ten longs make? They make a flat.
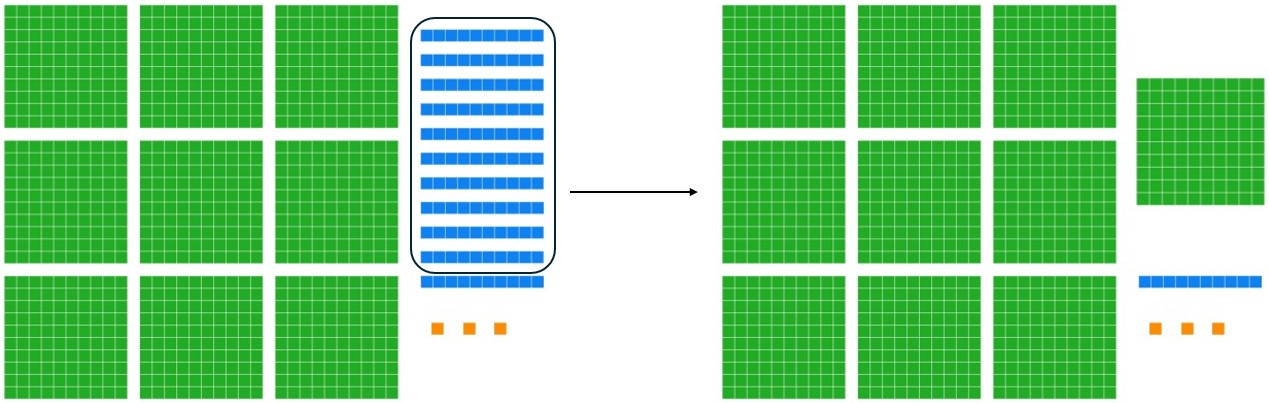
Now we have ten flats, 1 long, and 3 units. This means we have ten hundreds, 1 ten, and 3 ones. What can we do with the ten flats? We write ten as 10, which is "one group of ten," so we need to group those ten flats to create... a cube! That means our blocks now look like the following.
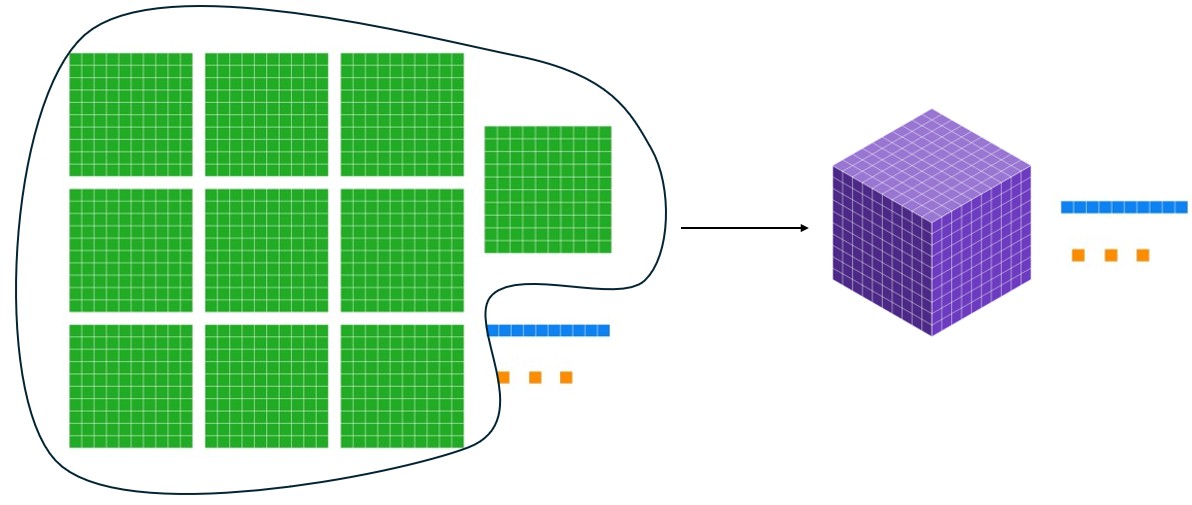
We have 1 one thousand, 0 hundreds, 1 ten, and 3 ones. So our number is 1013.
Scenario 5
Rodrigo lists the expanded form of 5824 as
[latex](5\times 30)+(8\times 20)+(2\times 10)+(4\times 1).[/latex]
What is his misconception? Explain to him both why his way doesn't work and what the correct way is.
Solution
Misconception: Instead of using powers of ten for the place values, Rodrigo is trying to use multiples of ten.
Conversation: Let's look at the blocks for 5824.
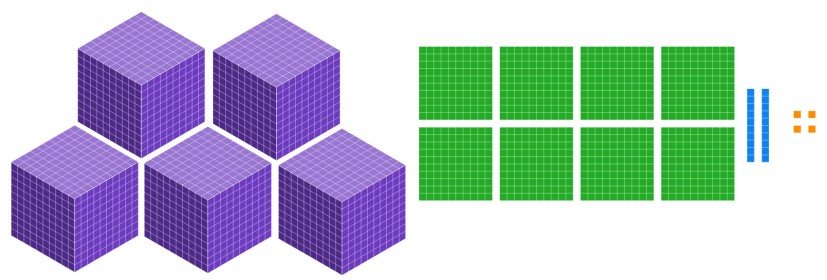
What is the size of each block? The 4 units each have a value of 1, so you were correct to say 4[latex]\times[/latex]1. The 2 longs each have a value of 10, so you were also correct to say 2[latex]\times[/latex]10. What is the value of each of the 8 flats? Do they have a value of 20 like you put in your expanded form? The value of each piece is 100, so it should be 8[latex]\times[/latex]100. Let's look at the cubes. You put 5[latex]\times[/latex]30. What do you think now? Should it be 30? It should be 1000 because that is the value of each cube. So our expanded form is
[latex](5\times 1000)+(8\times 100)+(2\times 10)+(4\times 1).[/latex]
The expanded form is showing each place value, and those should be powers of ten, not multiples of ten.
Scenario 6
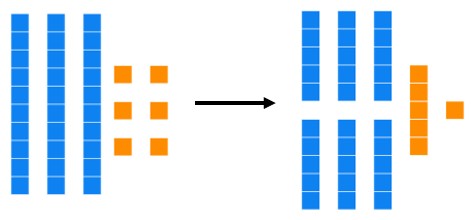
In a hypothetical future, some obscure study shows that students who learn base five in elementary school do better in life, so the government mandates all students learn both base five and base ten. Franklin says that 36 converted to base five is 71[latex]_{\text{five}}[/latex]. He explains his answer by breaking each base ten long into two base five longs as seen below. What does he understand well? What is he not understanding yet?
Solution
Misconception: Franklin understands the difference between base ten longs and base five longs. He also understands how to combine five units and make a long. What he missed was that there are enough base five longs to trade to create a base five flat.
Conversation: You started correctly, by combining five units to make a long. You were also correct to rearrange the longs from size ten to size five, but the problem isn't finished yet! How many base five longs do you have? Since we are in base five, you need to trade whenever you have five of something. So, trade 5 of the 7 base five longs to make a flat. Now you have 1 flat, 2 longs, and 1 unit. So, the base ten number 36 translated into base five is 121[latex]_{\text{five}}[/latex].
One quick way to check yourself is if you have any of the digits 5, 6, 7, 8, or 9 in your base five number. If so, that means you forgot to trade!
