13 Module 2.1 Numbers and Numerals
You will need: A-blocks (Material Cards 2A, 2B, 2C, 2D)
Imagine you came across a person from a remote English-speaking colony where everyone had three fingers on each hand. Although the people of this colony were intelligent, they had never heard of counting and did not know what it was, what it meant, or how to do it. They knew nothing about numbers, what they were, what they were called or what they looked like. Think about how you might teach this person about counting and numbers so they could go back and share this wonderful knowledge with their friends. What tools would you use to teach? What are some of the concepts you would have to get across? What difficulties might arise? Do you think this would be an easy or hard task? Write down some of your ideas, strategies, and conclusions.
What do you remember about learning about numbers or how to count? Have you ever helped to teach a young child how to count? They can say "1, 2, 3, 4, 5" at a young age, but when do they start to connect what those words mean?
Most of us in the modern world pretty much take the concept of numbers and counting for granted. In fact, we take language for granted –but that topic is too involved to go into right now. Imagine what a breakthrough it was when people first thought to give names to objects. Eventually, they used words, which we will call number names, to describe sets of objects (remember sets?!) in terms of their size. This was a considerable mathematical advancement. Although there are still some cultures that have not assigned names for numbers larger than three, most cultures have developed this concept. Some tribes even have different number names for different types of objects.
One difficulty with the concept of numbers as we use them today is that they are concepts and not necessarily used only for counting objects. The number four, for instance, is used in many ways –four years old, room 4, four feet high, 4 children, four hours, four minutes after eight, mail station 4, 4 fingers, a grade of 4 on a quiz, count to 4, four times bigger than something, 4th place, four wishes, fourth in line, call 444-4444, code 44, etc.
So, what is a number?
Definition - Number, Numeral
For example, the number three is the concept of three items. The symbol 3 is a numeral representing the concept three. You can't see or touch a number. The symbols that we see and touch that are used to represent numbers are numerals. In our culture, we use the Hindu-Arabic system where the numerals are made up of one or more of these ten symbols –0,1,2,3,4,5,6,7,8 and 9. For instance, in the Hindu-Arabic system, the number two million is represented by writing the numeral two million, which we write like this: 2,000,000. Notice, it took one symbol to write the number for three and seven symbols to write the number for two million (we don't count the commas as symbols because they aren't essential to writing the numeral). Although it took seven symbols to write the numeral two million, note that there are only two different symbols used to write that numeral –a two (2) and a zero (0).
Exercise 1
In your own words, describe the word number.
In your own words, describe the word numeral.
Teaching Tip: One of the biggest hurdles new teachers face is how to put mathematics into words. Show your answer to exercise 1 to a friend, roommate, or family member. Does it make sense to them? If not, revise your descriptions. The more you practice putting concepts and processes into words, the better prepared you will be!
There are three common uses of numbers. Describing how many elements are in a finite set is the most common use of the counting numbers. When used this way, the number is referred to as a cardinal number. Another way numbers are used concerns order. For instance, someone might be the fifth place winner or you might be eighth in line. When used in this way, numbers are called ordinal numbers. There are also numbers used for identification, such as your phone number, zip code, social security number or credit card number. These are called identification numbers and it is the actual order of the symbols that is important –not the value of the number.
One-to-One Correspondences and Matchings
When people recognized that a collection of four pebbles and a collection of four bananas had a common property, they were learning the concept of matching. The number four is an abstraction of this process. One of the best ways to see this is through the use of sets.
Exercise 2
Example 1
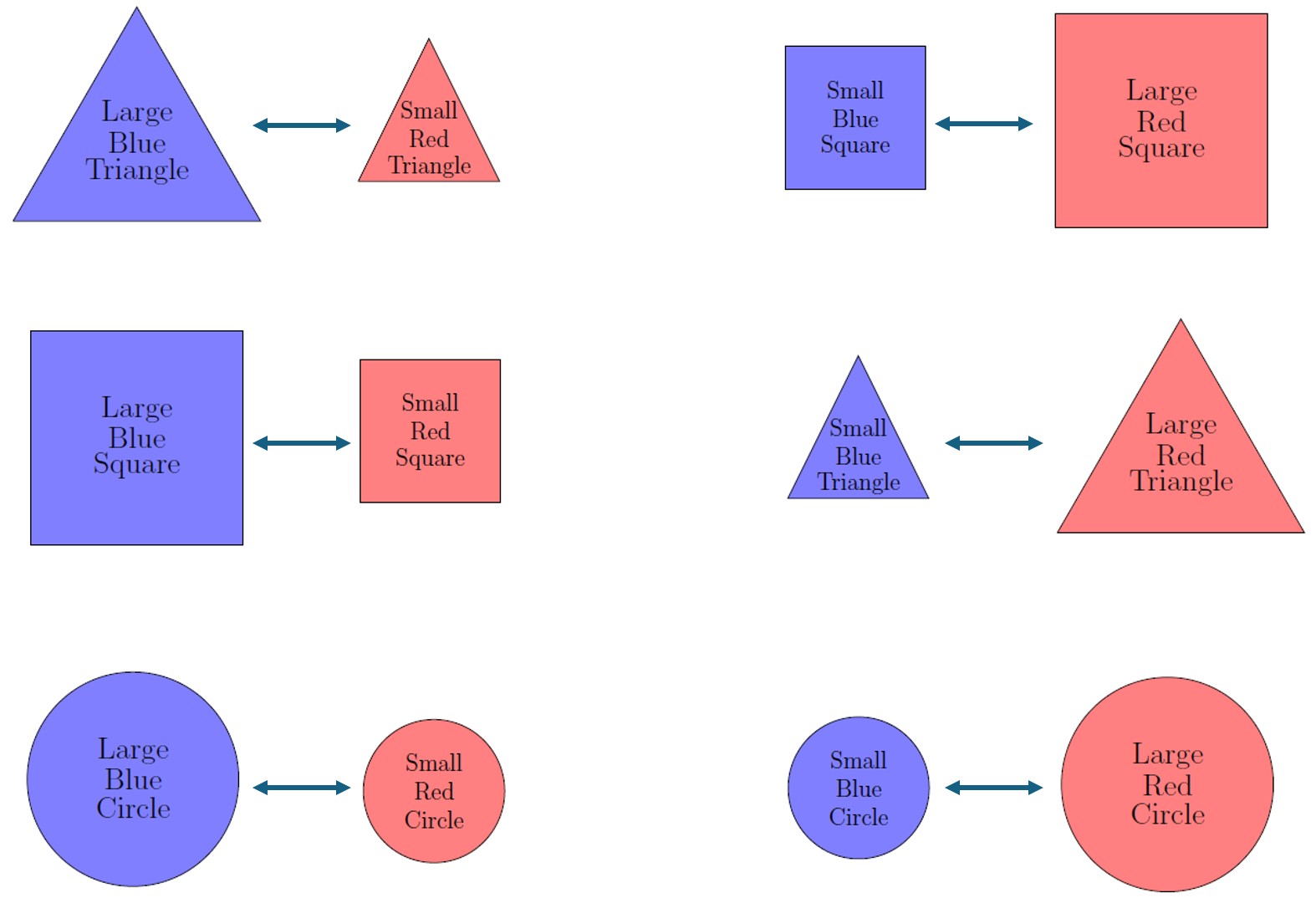
Find two more ways of matching the Red A-Blocks with the Blue A-Blocks.
(There are actually 720 different matchings possible!)
We say that the set of Blue A-blocks match the set of Red A-blocks because we can pair each element of the Blue A-blocks with exactly one element of the Red A-blocks and we do not have any pieces leftover.
NOTE: Two sets that match DO NOT have to match in a natural or pleasing way, the way we might match the colors of our clothes together. It might be easier to think of the word pairing instead. Think of showing a matching between two sets up by taking one element in the first set and pairing it up to dance with one element in the second set. Now that they are "dancing" together, take another element from the first set and pick someone in the second set for it to dance with. Continue doing this until all elements are have a partner. This is a matching! If your first set had 5 girls and your second set had 4 boys, they wouldn't match because one girl would be left without a partner. That is why it is necessary to have the same number of elements in each set to represent a matching.
Each of the pairings we have matched so far illustrates a one-to-one correspondence (1-1) between two sets. We say that two sets match if there is a one-to-one correspondence between their elements.
Exercise 3
- Is it possible to find a 1-1 correspondence between the sets [latex]\{2,3,5,7\}[/latex] and [latex]\{a,b,c,d\}[/latex]?
- Is it possible to find a 1-1 correspondence between the sets [latex]\{10, 20, 30\}[/latex] and [latex]\{a,b,c,d\}[/latex]?
- If a 1-1 correspondence between two sets exists, what does that imply about the cardinality of the two sets?
Solution
- Yes! One example would be
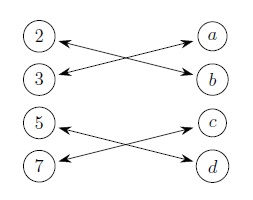
- It is not possible to find a 1-1 correspondence. No matter how you try, the set [latex]\{a,b,c,d\}[/latex] will always have one element without a partner.
- The sets must have the same cardinality.
Definition - One-to-One Correspondence
Two finite sets have a one-to-one correspondence if they have the same cardinality. We say set [latex]A[/latex] matches set [latex]B[/latex].
Exercise 4
Draw a one-to-one correspondence between the elements of the two sets below.
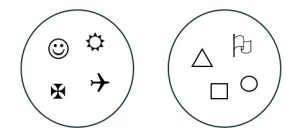
(Answers will vary)
To show all of the 1-1 correspondences, or matchings between two sets, think of all the ways two sets might partner up to do a single dance on the dance floor. Everyone from each set gets exactly one partner from the other set to dance with, and everyone gets to dance. For instance, think of a group of 4 boys–A, B, C and D and 4 girls–W, X, Y and Z. Each boy needs to be paired up with one girl for a dance, so there will be four couples dancing for one dance. One matching would be to show how they pair up for that one dance: maybe A with X, B with Z, C with W and D with Y –that is Matching 11, as shown below. That's only one matching. Note that you do not pair up an element of one set with an element of the same set. For this example, that means a girl only dances with a boy. To show ALL possibilities for this example, you'd have to list all the different ways they might end up as couples on the dance floor for one dance. Each matching shows the four couples, as they are paired up for one dance. To be a different matching, at least two couples would have changed partners. There are actually 24 possible 1-1 correspondences (or different matchings) for this example of four boys and four girls. Below is one way to list all of these possibilities:
First Couple |
Second Couple |
Third Couple |
Fourth Couple |
|
Pairing 1 |
A [latex]\leftrightarrow[/latex] W | B [latex]\leftrightarrow[/latex] X | C [latex]\leftrightarrow[/latex] Y | D [latex]\leftrightarrow[/latex] Z |
Pairing 2 |
A [latex]\leftrightarrow[/latex] W | B [latex]\leftrightarrow[/latex] X | C [latex]\leftrightarrow[/latex] Z | D [latex]\leftrightarrow[/latex] Y |
Pairing 3 |
A [latex]\leftrightarrow[/latex] W | B [latex]\leftrightarrow[/latex] Y | C [latex]\leftrightarrow[/latex] X | D [latex]\leftrightarrow[/latex] Z |
Pairing 4 |
A [latex]\leftrightarrow[/latex] W | B [latex]\leftrightarrow[/latex] Y | C [latex]\leftrightarrow[/latex] Z | D [latex]\leftrightarrow[/latex] X |
Pairing 5 |
A [latex]\leftrightarrow[/latex] W | B [latex]\leftrightarrow[/latex] Z | C [latex]\leftrightarrow[/latex] X | D [latex]\leftrightarrow[/latex] Y |
Pairing 6 |
A [latex]\leftrightarrow[/latex] W | B [latex]\leftrightarrow[/latex] Z | C [latex]\leftrightarrow[/latex] Y | D [latex]\leftrightarrow[/latex] X |
Pairing 7 |
A [latex]\leftrightarrow[/latex] X | B [latex]\leftrightarrow[/latex] W | C [latex]\leftrightarrow[/latex] Y | D [latex]\leftrightarrow[/latex] Z |
Pairing 8 |
A [latex]\leftrightarrow[/latex] X | B [latex]\leftrightarrow[/latex] W | C [latex]\leftrightarrow[/latex] Z | D [latex]\leftrightarrow[/latex] Y |
Pairing 9 |
A [latex]\leftrightarrow[/latex] X | B [latex]\leftrightarrow[/latex] Y | C [latex]\leftrightarrow[/latex] W | D [latex]\leftrightarrow[/latex] Z |
Pairing 10 |
A [latex]\leftrightarrow[/latex] X | B [latex]\leftrightarrow[/latex] Y | C [latex]\leftrightarrow[/latex] Z | D [latex]\leftrightarrow[/latex] W |
Pairing 11 |
A [latex]\leftrightarrow[/latex] X | B [latex]\leftrightarrow[/latex] Z | C [latex]\leftrightarrow[/latex] W | D [latex]\leftrightarrow[/latex] Y |
Pairing 12 |
A [latex]\leftrightarrow[/latex] X | B [latex]\leftrightarrow[/latex] Z | C [latex]\leftrightarrow[/latex] Y | D [latex]\leftrightarrow[/latex] W |
Pairing 13 |
A [latex]\leftrightarrow[/latex] Y | B [latex]\leftrightarrow[/latex] W | C [latex]\leftrightarrow[/latex] X | D [latex]\leftrightarrow[/latex] Z |
Pairing 14 |
A [latex]\leftrightarrow[/latex] Y | B [latex]\leftrightarrow[/latex] W | C [latex]\leftrightarrow[/latex] Z | D [latex]\leftrightarrow[/latex] X |
Pairing 15 |
A [latex]\leftrightarrow[/latex] Y | B [latex]\leftrightarrow[/latex] X | C [latex]\leftrightarrow[/latex] W | D [latex]\leftrightarrow[/latex] Z |
Pairing 16 |
A [latex]\leftrightarrow[/latex] Y | B [latex]\leftrightarrow[/latex] X | C [latex]\leftrightarrow[/latex] Z | D [latex]\leftrightarrow[/latex] W |
Pairing 17 |
A [latex]\leftrightarrow[/latex] Y | B [latex]\leftrightarrow[/latex] Z | C [latex]\leftrightarrow[/latex] W | D [latex]\leftrightarrow[/latex] X |
Pairing 18 |
A [latex]\leftrightarrow[/latex] Y | B [latex]\leftrightarrow[/latex] Z | C [latex]\leftrightarrow[/latex] X | D [latex]\leftrightarrow[/latex] W |
Pairing 19 |
A [latex]\leftrightarrow[/latex] Z | B [latex]\leftrightarrow[/latex] W | C [latex]\leftrightarrow[/latex] X | D [latex]\leftrightarrow[/latex] Y |
Pairing 20 |
A [latex]\leftrightarrow[/latex] Z | B [latex]\leftrightarrow[/latex] W | C [latex]\leftrightarrow[/latex] Y | D [latex]\leftrightarrow[/latex] X |
Pairing 21 |
A [latex]\leftrightarrow[/latex] Z | B [latex]\leftrightarrow[/latex] X | C [latex]\leftrightarrow[/latex] W | D [latex]\leftrightarrow[/latex] Y |
Pairing 22 |
A [latex]\leftrightarrow[/latex] Z | B [latex]\leftrightarrow[/latex] X | C [latex]\leftrightarrow[/latex] Y | D [latex]\leftrightarrow[/latex] W |
Pairing 23 |
A [latex]\leftrightarrow[/latex] Z | B [latex]\leftrightarrow[/latex] Y | C [latex]\leftrightarrow[/latex] W | D [latex]\leftrightarrow[/latex] X |
Pairing 24 |
A [latex]\leftrightarrow[/latex] Z | B [latex]\leftrightarrow[/latex] Y | C [latex]\leftrightarrow[/latex] X | D [latex]\leftrightarrow[/latex] W |
If you were asked to list one matching between two sets {A, B, C, D} and {W, X, Y, Z}, any of the 24 matchings shown above would be fine. However, if you are asked to list ALL possibilities, you must be very clear about what constitutes a matching, as I've illustrated above. In each matching, note that the individual couples (who is dancing with whom) must be shown. If the sets have one element each, then each matching has one pairing. If the sets have two elements each, then each matching has two pairings. If the sets have three elements each, then each matching has three pairings. And, if the sets have four elements each (as in the example above), then each matching has four pairings.
Exercise 5
Show every possible 1-1 correspondence (or matching) between the sets.
- [latex]\{1\} \text{ and } \{A\}[/latex]
- [latex]\{2,3\} \text{ and } \{B,C\}[/latex]
- [latex]\{4,5,6\} \text{ and } \{D,E,F\}[/latex]
Solution
- Only one option: [latex]1 \leftrightarrow A[/latex]
- Two options: [latex]\;2\leftrightarrow B[/latex] and [latex]3\leftrightarrow C[/latex]
[latex]\qquad\qquad\quad 2\leftrightarrow C[/latex] and [latex]3\leftrightarrow B[/latex] - Six options: [latex]4\leftrightarrow D[/latex], [latex]5\leftrightarrow E[/latex], and [latex]6\leftrightarrow F[/latex]
[latex]\;\qquad\qquad4\leftrightarrow D[/latex], [latex]5\leftrightarrow F[/latex], and [latex]6\leftrightarrow E[/latex]
[latex]\;\qquad\qquad4\leftrightarrow E[/latex], [latex]5\leftrightarrow D[/latex], and [latex]6\leftrightarrow F[/latex]
[latex]\;\qquad\qquad4\leftrightarrow E[/latex], [latex]5\leftrightarrow F[/latex], and [latex]6\leftrightarrow D[/latex]
[latex]\;\qquad\qquad4\leftrightarrow F[/latex], [latex]5\leftrightarrow D[/latex], and [latex]6\leftrightarrow E[/latex]
[latex]\;\qquad\qquad4\leftrightarrow F[/latex], [latex]5\leftrightarrow E[/latex], and [latex]6\leftrightarrow D[/latex]
Concept Check: If you change part c in exercise 5 to [latex]\{4,5,6\} \text{ and } \{4,5,6\}[/latex], how many 1-1 correspondences are there?
Solution
There are still six of them! It doesn't matter what items are in the sets, there are always six ways to match sets with three elements each.
[latex]4\leftrightarrow 4[/latex], [latex]5\leftrightarrow 5[/latex], [latex]6\leftrightarrow 6[/latex]
[latex]4\leftrightarrow 4[/latex], [latex]5\leftrightarrow 6[/latex], [latex]6\leftrightarrow 5[/latex]
[latex]4\leftrightarrow 5[/latex], [latex]5\leftrightarrow 4[/latex], [latex]6\leftrightarrow 6[/latex]
[latex]4\leftrightarrow 5[/latex], [latex]5\leftrightarrow 6[/latex], [latex]6\leftrightarrow 4[/latex]
[latex]4\leftrightarrow 6[/latex], [latex]5\leftrightarrow 4[/latex], [latex]6\leftrightarrow 5[/latex]
[latex]4\leftrightarrow 6[/latex], [latex]5\leftrightarrow 5[/latex], [latex]6\leftrightarrow 4[/latex]
Exercise 6
- [latex]\{M\}[/latex] and [latex]\{M\}[/latex]
- [latex]\{x,y\}[/latex] and [latex]\{x,z\}[/latex]
- [latex]\{1,2,3\}[/latex] and [latex]\{1,2,3\}[/latex]
- [latex]\{1,2,3\}[/latex] and [latex]\{3,4,5\}[/latex]
Solution
a. [latex]M\leftrightarrow M[/latex]
b. [latex]x\leftrightarrow x, y\leftrightarrow z[/latex]
[latex]\quad x\leftrightarrow z, y\leftrightarrow x[/latex]
c. [latex]1\leftrightarrow 1, 2\leftrightarrow 2, 3\leftrightarrow 3[/latex]
[latex]\quad 1\leftrightarrow 1, 2\leftrightarrow 3, 3\leftrightarrow 2[/latex]
[latex]\quad 1\leftrightarrow 2, 2\leftrightarrow 1, 3\leftrightarrow 3[/latex]
[latex]\quad 1\leftrightarrow 2, 2\leftrightarrow 3, 3\leftrightarrow 1[/latex]
[latex]\quad 1\leftrightarrow 3, 2\leftrightarrow 1, 3\leftrightarrow 2[/latex]
[latex]\quad 1\leftrightarrow 3, 2\leftrightarrow 2, 3\leftrightarrow 1[/latex]
d. [latex]1\leftrightarrow 3, 2\leftrightarrow 4, 3\leftrightarrow 5[/latex]
[latex]\quad 1\leftrightarrow 3, 2\leftrightarrow 5, 3\leftrightarrow 4[/latex]
[latex]\quad 1\leftrightarrow 4, 2\leftrightarrow 3, 3\leftrightarrow 5[/latex]
[latex]\quad 1\leftrightarrow 4, 2\leftrightarrow 5, 3\leftrightarrow 3[/latex]
[latex]\quad 1\leftrightarrow 5, 2\leftrightarrow 3, 3\leftrightarrow 4[/latex]
[latex]\quad 1\leftrightarrow 5, 2\leftrightarrow 4, 3\leftrightarrow 3[/latex]
When considering 1-1 correspondences, there are a few properties that stand out.
Properties of Matching
- A set always matches itself.
- For any two sets, [latex]A[/latex] and [latex]B[/latex], if [latex]A[/latex] matches [latex]B[/latex], then [latex]B[/latex] matches [latex]A[/latex].
- For any three sets, [latex]A[/latex], [latex]B[/latex], and [latex]C[/latex], if [latex]A[/latex] matches [latex]B[/latex] and [latex]B[/latex] matches [latex]C[/latex], then [latex]A[/latex] matches [latex]C[/latex].
Exercise 7
Illustrate Property 3 by creating matchings between the following three sets from your A-blocks:
A: the set of small circles
B: the set of small triangles
C: the set of small squares.
Describe your matchings by listing the abbreviations (SRC, etc.) or drawing the picture for each of the individual elements in each set. Three separate matchings, each having 4 pairings, should be shown. The first matching should show one matching between A and B, then there should be another matching shown between B and C. Last, there should be a matching shown between A and C.
(Answers will vary.)
Now that we have seen the abstract concept behind numbers, let's explore how we represent them with numerals.
Exploring Numeration Systems
Today, most but not all civilizations around the world use the Hindu-Arabic system of counting and numerals 1,2,3,4,5,6,7,8,9,10,11,12,... There are many advantages to this number system. While you might think this common, widely used system of counting the obvious choice, you might consider both the advantages and disadvantages of Hindu-Arabic as we learn about other numeration systems.
STROKE System
In the STROKE system, there is only one symbol, a simple vertical stroke. A number is represented by that amount of vertical strokes.
Here are the first ten numbers in STROKE:
| Number | Representation in STROKE |
|---|---|
| One | | |
| Two | | | |
| Three | | | | |
| Four | | | | | |
| Five | | | | | | |
| Six | | | | | | | |
| Seven | | | | | | | | |
| Eight | | | | | | | | | |
| Nine | | | | | | | | | | |
| Ten | | | | | | | | | | | |
Exercise 8
a. Show how you would write the numeral eleven in STROKE.
Solution
| | | | | | | | | | |
b. Describe in words how to write the numerals five hundred twelve; and two million in STROKE.
Solution
You would need five hundred twelve strokes. You would need two million strokes.
c. What are some advantages of the STROKE system?
Solution
It is easy to learn. There is only one symbol, and you can see the connection to what the number means. (The number five is shown with five items.)
d. What are some disadvantages of the STROKE system?
Solution
It is not feasible to write out large numbers. Also, for smaller numbers like twenty and twenty-one, you cannot quickly tell the difference between them.
The tally system improved the STROKE system by introducing the concept of grouping. You are probably familiar with this system, where the fifth stroke was placed across the previous four, so it would be easier to read since you can count by fives. STROKE is a single symbol system, but Tally can be thought of as a two symbol system, although the second symbol is really just made up of five strokes.
Tally System
Here are the first ten numbers in Tally:
| Number | Representation in Tally |
|---|---|
| One | [latex]|[/latex] |
| Two | [latex]||[/latex] |
| Three | [latex]|||[/latex] |
| Four | [latex]||||[/latex] |
| Five | [latex]\cancel{||||}[/latex] |
| Six | [latex]\cancel{||||}\;|[/latex] |
| Seven | [latex]\cancel{||||}\;||[/latex] |
| Eight | [latex]\cancel{||||}\;|||[/latex] |
| Nine | [latex]\cancel{||||}\;||||[/latex] |
| Ten | [latex]\cancel{||||}\;\cancel{||||}[/latex] |
Note the difference in writing the numeral twenty-eight in the two systems.
STROKE: [latex]||||||||||||||||||||||||||||[/latex]
Tally: [latex]\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}\cancel{||||}|||[/latex]
Exercise 9
a. Write the numeral for 17 in STROKE.
Solution
[latex]|||||||||||||||||[/latex]
b. Write the numeral for 17 in Tally.
Solution
[latex]\cancel{||||}\;\cancel{||||}\;\cancel{||||}\;||[/latex]
Concept Check: How many symbols does it take to express the number one hundred seventy-two in Tally?
Solution
It will take thirty-six symbols: thirty-four will be groups of five and two will be single strokes.
Both the STROKE and Tally systems are cumbersome for large numbers. As civilizations began to write more and more, they needed better ways to express numbers. Some classic examples come from ancient Egypt, Roman times, Mayan civilization, and China. Mayan and Chinese systems are more closely related to our Hindu-Arabic system, so we will explore them in the next section.
Ancient Egypt used pictures called hieroglyphics for all of their writing, including numbers. This system was developed around 3400 B.C. When a group of pictures is put together, you add their value to determine what number is represented. Order does not matter, and they do not need to be listed in a horizontal line.
Old Egyptian Numeral System
The Old Egyptian numeral system employs an additive system of counting using the seven symbols below.
Number |
Representation in Hieroglyphics |
What the picture is |
| One | Staff | |
| Ten | Heel Bone | |
| Hundred | Scroll/Coil | |
| Thousand | Lotus Flower | |
| Ten-thousand | Pointing Finger | |
| Hundred-thousand | Polliwog/Tadpole | |
| Million | Astonished Man |
| Number | Representation in Egyptian |
|---|---|
| One | | |
| Two | | | |
| Three | | | | |
| Four | | | | | |
| Five | | | | | | |
| Six | | | | | | | |
| Seven | | | | | | | | |
| Eight | | | | | | | | | |
| Nine | | | | | | | | | | |
| Ten | [latex]\bigcap[/latex] |
Here are three different ways to write the numeral sixty-five in the Old Egyptian system:
(heel bone, heel bone, heel bone, heel bone, heel bone, heel bone, staff, staff, staff, staff, staff)
(heel bone, heel bone, staff, staff, heel bone, staff, heel bone, heel bone, staff, staff, heel bone)
or as shown below, with all the symbols enclosed in a visual set
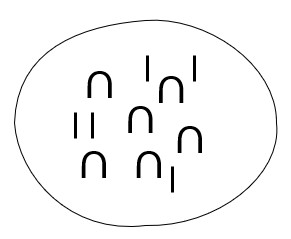
You simply add up the values of each of the symbols to get the answer.
Definition - Additive Principle
The additive principle states that the value of a set of symbols is the sum of the values of the symbols.
In this additive system, the Egyptian numeral
(astonished man, pointing finger, lotus flower, lotus flower, lotus flower, scroll/coil, scroll/coil, staff, staff, staff, staff)
represents 1,000,000 + 10,000 + 1,000 + 1,000 + 1,000 + 100 + 100 + 1 + 1 + 1 + 1 = 1,013,204.
Remember: The order in which the symbols are written is irrelevant in an additive system.
Exercise 10
Write the numeral one hundred twenty-two using two different combinations of Egyptian symbols.
Solution
One option:
(scroll/coil, heel bone, heel bone, staff, staff)
Another option:
(scroll/coil, scroll/coil, scroll/coil, scroll/coil, scroll/coil, scroll/coil, scroll/coil, scroll/coil, scroll/coil, scroll/coil, staff, staff)
Exercise 11
a. (heel bone, heel bone, lotus flower, polliwag/tadpole, polliwag/tadpole, polliwag/tadpole)
(astonished man, astonished man, astonished man, astonished man, scroll/coil, scroll/coil, staff, staff, staff, staff, staff, staff, staff, pointing finger, scroll/coil, scroll/coil scroll/coil)
(lotus flower, lotus flower, lotus flower, lotus flower, lotus flower, lotus flower, lotus flower, lotus flower, lotus flower, lotus flower, lotus flower, lotus flower, lotus flower, lotus flower, lotus flower, pointing finer, pointing finger)
(pointing finger, heel bone, heel bone, polliwag/tadpole, staff, staff, staff)
Exercise 12
Solution
𓏲𓏲𓏲𓏲
(scroll/coil, scroll/coil, scroll/coil, scroll/coil, staff, staff, staff, staff, staff, staff, staff)
Solution
(astonished man, astonished man, astonished man, pointing finger, pointing finger, pointing finger, pointing finger, pointing finger, lotus flower, heel bone, heel bone, heel bone, heel bone)
Solution
(polliwag/tadpole, polliwag/tadpole, polliwag/tadpole, pointing finger, pointing finger, pointing finger, lotus flower, lotus flower, scroll/coil, scroll/coil, scroll/coil, scroll/coil, scroll/coil, staff)
Solution
(astonished man, astonished man, astonished man, astonished man)
Solution
(astonished man, polliwag/tadpole, pointing finger, lotus flower, scroll/coil, heel bone, staff)
The Egyptian system employs the technique of grouping, where a certain number of the same symbols are grouped together and replaced with a new symbol. This is necessary to symbolize very large numbers efficiently. Systems that use this grouping principle are said to be of a certain base depending on how many symbols it takes to exchange to a new symbol. For instance, a system that groups six symbols together and then replaces them with a new symbol is said to be a Base Six system.
Exercise 13
a. In what base is the Egyptian system? What is the limitation of this system as far as grouping is concerned? (Think about how to write four trillion!)
Solution
It is in base ten, but stops at a symbol for a million. To write 4 trillion, you would need 4 million of the astonished man symbols. Even something like 99 requires 18 symbols, which is rather cumbersome.
b. Name some advantages and disadvantages of the Old Egyptian system compared with the Hindu-Arabic system, the STROKE system and the Tally system.
Solution
One advantage: The fact that order doesn't matter in the Egyptian system makes it easier to comprehend compared to the Hindu-Arabic system. For example, the numbers 23 and 32 are different, which requires extra knowledge beyond what 2 and 3 mean individually. But that is not an issue in the Egyptian system.
One disadvantage: There are lots of ways to represent one number in Egyptian. For example, the number 21 can be two tens and a one, one ten and eleven ones, or twenty-one ones. Also, since order doesn't matter, each of these three possibilities can be drawn in a variety of different ways. With Hindu-Arabic, STROKE, and Tally, each number has exactly one representation.
Thousands of years after hieroglyphics were developed, but hundreds of years before the Roman Empire, Roman numerals began to be used. Roman numerals are still used today on occasion, such as for bulleted lists, analog clocks, introductory page numbers in books, and even the Super Bowl!
The symbols used in the Roman Numeral System are
[latex]\text{I}[/latex] which represents one;
[latex]\text{V}[/latex] which represents five;
[latex]\text{X}[/latex] which represents ten;
[latex]\text{L}[/latex] which represents fifty;
[latex]\text{C}[/latex] which represents one hundred;
[latex]\text{D}[/latex] which represents five hundred;
[latex]\text{M}[/latex] which represents one thousand.
When it was first developed, the Roman numeral system was an additive system like the Egyptian system. It is actually a Base Ten system with additional symbols for 5, 50 and 500. These extra symbols significantly reduce the amount of writing one must do. For instance, writing the Roman numeral eight hundred eighty-seven without the use of the additional symbols would look like this: CCCCCCCCXXXXXXXXIIIIIII. Writing this same numeral using the additional symbols would look like this: DCCCLXXXVII. Without the V, L and D, one would need to write out more than twice as many symbols for this particular numeral.
Example 2
a. Write the Roman numeral DCCCLXXXVII as a Hindu-Arabic numeral.
Solution:
Replacing each letter with its equivalent value in Hindu-Arabic numerals we have
500 + 100 + 100 + 100 + 50 + 10 + 10 + 10 + 5 + 1 + 1 = 887.
b. Write the Hindu-Arabic numeral 673 as a Roman numeral using the least amount of symbols.
Solution:
The symbol with the largest value fitting into 673 is D which represents 500. So our first letter is D.
673 - 500 = 173
We have 173 remaining and the symbol with the largest value fitting into 173 is C which represents 100. So our next letter is C.
173 - 100 = 73
Continuing to break down our remaining 73 in the same fashion we get 50, 10, 10, 1, 1, and 1. Our final answer is
DCLXXIII
Exercise 14
Write each Hindu-Arabic numeral as a Roman numeral using the least amount of symbols:
a. 32
Solution
[latex]\text{XXXII}[/latex]
b. 561
Solution
[latex]\text{DLXI}[/latex]
c. 708
Solution
[latex]\text{CCCCCCCVIII}[/latex]
d. 2053
Solution
[latex]\text{MMLIII}[/latex]
Exercise 15
Write each Roman numeral as a Hindu-Arabic numeral.
a. [latex]\text{MMDCLXXXVII}[/latex]
b. [latex]\text{MCCXXXII}[/latex]
Example 3
Write the Hindu-Arabic numeral equivalent to the given Roman numeral.
a. [latex]\overline{\text{CCLVI}}\text{CCX}[/latex]
Solution:
The value under the bar is 100 + 100 + 50 + 5 + 1=256. Multiplying by 1000 gives 256,000. The remaining letters have value 100+100+10=210.
Answer: 256,210
b. [latex]\overline{\overline{\text{V}}}\;\overline{\text{LX}}\text{DX}[/latex]
Solution:
The value of V is 5, but it is under two bars, so we have 5 [latex]\times[/latex] 1000000 = 5,000,000. The LX is under one bar, so it has value (50 + 10) 1000 = 60,000. Finally, the last two letters have value 500 + 10 = 510.
Answer: 5,060,510
Exercise 16
Write each Hindu-Arabic numeral as a Roman numeral using the least amount of symbols possible.
a. 330,802
Solution
[latex]\overline{\text{CCCXXX}}\;\text{DCCCII}[/latex]
b. 70,001,651
Solution
[latex]\overline{\overline{\text{LXX}}}\;\text{MDCLI}[/latex]
Exercise 17
Write each Roman numeral as a Hindu-Arabic numeral.
a. [latex]\overline{\text{III}}\text{CCXII}[/latex]
b. [latex]\overline{\text{LX}}\text{DCL}[/latex]
Over time, the Roman numeration system developed a subtractive principle. If a symbol representing a smaller number is to the left of a symbol representing a larger number, then the total value of those two symbols together represents the value of the larger symbol minus the value of the smaller symbol. There were specific conditions. Only symbols representing powers of ten (I,X,C,M) could be subtracted and each of these four could only be paired with the next two larger symbols. So, the following are the only possibilities for using the subtractive principle:
[latex]\text{IV}[/latex] which represents four;
[latex]\text{IX}[/latex] which represents nine;
[latex]\text{XL}[/latex] which represents forty;
[latex]\text{XC}[/latex] which represents ninety;
[latex]\text{CD}[/latex] which represents four hundred;
[latex]\text{CM}[/latex] which represents nine hundred.
As you read a Roman numeral from left to right, use the additive principle. If a symbol denoting a smaller value precedes a symbol denoting a larger value, use the subtractive principle when reading those two symbols. Study the following examples.
Example 4
Write each of the following Roman numerals as a Hindu-Arabic numeral.
a. [latex]\text{CMXXXIX}[/latex]
Solution:
Notice that the values are 100, 1000, 10, 10, 10, 1, and 10. Since 100 is smaller than 1000 but is listed before 1000, we must subtract: 1000-100=900. Moving on we have 10+10+10, but then we see IX. Since one is smaller than ten and listed before the ten, we must subtract:10-1=9.
900+10+10+10+9=939
b. [latex]\overline{\text{XCIV}}\text{CCXCII}[/latex]
Solution:
Consider the bar first. We have XC and IV both of which fit the subtraction principle since the smaller value is listed first. Our total under the bar is (100-10)+(5-1)=94. Thus, the bar represents 94,000. Next, we have 100+100, but then XC which is 100-10=90. The last two symbols are 1+1.
94,000+100+100+90+1+1=94,292
Below is a summary of the Roman numeral system.
Roman Numeral System
The Roman numeral system assigns value to seven different letters. Whether the letter is upper or lowercase does not change its value.
Number |
Representation in Roman Numerals (Uppercase) |
Representation in Roman Numerals (Lowercase) |
| One | I | i |
| Five | V | v |
| Ten | X | x |
| Fifty | L | l |
| One hundred | C | c |
| Five hundred | D | d |
| One thousand | M | m |
The Roman numeral system uses additive, multiplicative, and subtractive principles. The values of all listed symbols are added unless
- Some symbols are under a bar. These symbols are totaled and then multiplied by 1000 before being added to the whole numeral's total.
- I, X, or C is listed before a symbol of larger value. In this case, the smaller symbol's value is subtracted from the larger symbol's value before adding to the whole numeral's total.
| Number | Representation in Roman Numerals |
|---|---|
| One | [latex]\text{I}[/latex] |
| Two | [latex]\text{II}[/latex] |
| Three | [latex]\text{III}[/latex] |
| Four | [latex]\text{IV}[/latex] |
| Five | [latex]\text{V}[/latex] |
| Six | [latex]\text{VI}[/latex] |
| Seven | [latex]\text{VII}[/latex] |
| Eight | [latex]\text{VIII}[/latex] |
| Nine | [latex]\text{IX}[/latex] |
| Ten | [latex]\text{X}[/latex] |
Exercise 18
Exercise 19
Rewrite each Roman numeral using the least number of symbols possible and the subtractive principle where applicable.
a. [latex]\text{CCCCCCCXXXXIIIIIIII}[/latex]
Solution
[latex]\text{DCCXLVIII}[/latex]
b. [latex]\text{MMMMMMMMMMMMMMCCCCXXXXXXXX}[/latex]
Solution
[latex]\overline{\text{XIV}}\;\text{CDLXXX}[/latex]
c. [latex]\text{CCCCCCCCCXXXXXXIIIIIIIII}[/latex]
Solution
[latex]\text{CMLXIX}[/latex]
d. [latex]\text{CCCCXXXXII}[/latex]
Solution
[latex]\text{CDXLII}[/latex]
Exercise 20
Write each Hindu-Arabic numeral as a Roman numeral using the least number of symbols possible and the subtractive principle where applicable.
a. 19,453
Solution
[latex]\overline{\text{XIX}}\;\text{CDLIII}[/latex]
b. 2,849
Solution
[latex]\text{MMDCCCXLIX}[/latex]
c. 1,996
Solution
[latex]\text{MCMXCVI}[/latex]
From now on, because this is how they are used today, write all Roman numerals using the least number of symbols possible and the subtractive principle where applicable, unless you are otherwise instructed.
Concept Check: When using Roman numerals and the multiplicative and subtractive principles:
What is the most times the symbol "I" can be repeated in a row?
What about "V"?
What about "X"?
What about "L"?
What about "C"?
What about "D"?
Solution
I - Three times (If you list IIII, you should have used IV or IX)
V - Once (If you list VV, you should have used X)
X - Three times (If you list XXXX, you should have used XL)
L - Once (If you list LL, you should have used C)
C - Three times (If you list CCCC, you should have used CD)
D - Once (If you list DD, you should have used M)
In the next section we will look at two more systems, but for now we'll end this section by comparing the systems we have worked with so far. First, we will consider the number of symbols one has to memorize in order to understand each individual system. We will then determine how many symbols one has to write down in order to represent various numerals in the different systems.
Exercise 21
For each of the numeration systems we've learned about so far, state how many different symbols a person has to memorize to understand the system. For Roman, do not consider symbols with bars over them as different symbols.
a. Hindu-Arabic
Solution
Ten symbols - 0,1,2,3,4,5,6,7,8,9
b. STROKE
Solution
One symbol
c. Tally
Solution
Two symbols
d. Egyptian
Solution
Seven symbols
e. Roman
Solution
Seven symbols (or eight if you count the bar that goes over the letters)
Let's write the numeral 67 in the different systems and note how many total symbols (not necessarily different symbols) it takes to express the number 67 in each system.
System |
What we write |
Number of symbols |
| Hindu-Arabic | 67 | 2 |
| STROKE | [latex]|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||[/latex] | 67 |
| Tally | [latex]\cancel{||||}\;\cancel{||||}\;\cancel{||||}\;\cancel{||||}\;\cancel{||||}\;\cancel{||||}\;\cancel{||||}\;\cancel{||||}\;\cancel{||||}\;\cancel{||||}\;\cancel{||||}\;\cancel{||||}\;\cancel{||||} \;||[/latex] | 15 |
| Egyptian | [latex]\bigcap\bigcap\bigcap\bigcap\bigcap\bigcap |||||||[/latex] | 13 |
| Roman | [latex]\text{LXVII}[/latex] | 5 |
Exercise 22
Write the numeral for 900 in each of the five systems below and state how many symbols it takes to write out the full numeral. Rather than writing the numerals in STROKE and Tally, explain in words how you would write them, still indicating the total number of symbols that would have to be written.
a. Hindu-Arabic
Solution
900 (three symbols)
b. STROKE
Solution
It would take nine hundred [latex]|[/latex] symbols.
c. Tally
Solution
It would take 180 of the symbols for five.
d. Egyptian
Solution
𓏲𓏲𓏲𓏲𓏲𓏲𓏲𓏲𓏲 (nine scroll/coil symbols)
There are lots of possible solutions, but nine is the fewest number of symbols that work.
e. Roman
Solution
[latex]\text{CM}[/latex] (two symbols)
Exercise 23
For each Hindu-Arabic number, state the least number of symbols it takes to write the numeral in each of the given numeration systems. Some answers are filled in for you. You don't need to actually write the numeral –just determine how many symbols you would have to write down if you were going to write the numeral. Write your answer in Hindu-Arabic.
a. 143
b. 400
c. 1,000,000
d. 30,009
e. 2,124
