18 Homework
For each two sets noted, indicate whether or not the sets match. If they do, show a matching. If they do not, explain why not.
a. Small Blue A-blocks and Large Red A-Blocks
b. Yellow A-blocks and Circular A-blocks
Describe a matching between the set of counting numbers, {1, 2, 3, ...} and the set of positive multiples of five, {5, 10, 15, ...}.
Show every possible one-to-one correspondence between the Small Blue A-blocks and the Small Red A-blocks. Use abbreviations or pictures to denote the blocks.
Convert each numeral to a Hindu-Arabic Base Ten numeral.
-
- STROKE: | | | | | | | | | | | | | | | |
- Tally: [latex]\cancel{||||}\cancel{||||}\cancel{||||} |||[/latex]
- Roman: MCMLXII
- Roman: DCCXLIV
- Roman: [latex]\overline{\overline{\text{IV}}}\overline{\text{CCX}}[/latex]DLI
- Egyptian:
(astonished man, pointing finger, pointing finger, astonished man, lotus flower, heel bone, heel bone, astonished man, pointing finger) - Chinese:

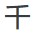
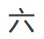
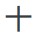
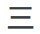
-
- Mayan:
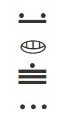
- [latex]4032_{\text{seven}}[/latex]
- [latex]\text{T}6\text{W}_{\text{thirteen}}[/latex]
- [latex]1 111 001 011_{\text{two}}[/latex]
- [latex]507_{\text{nine}}[/latex]
- Mayan:
Convert 342 to a numeral in the numeration system or base specified.
- Roman
- Base Seven
- Egyptian
- Bast Two
- Chinese
Convert 838 to:
- Base Twelve
- Base Eight
- Base Five
- Mayan
Convert 13,595 to Base Twelve
Convert 120,258 to Mayan
Count from 620 to 630 in Base Five
State the numeral that comes just before:
- [latex]173 425 760_{\text{eleven}}[/latex]
- [latex]2 010 212 000_{\text{four}}[/latex]
State the numeral that comes right after:
- [latex]539100\text{TE}_{\text{twelve}}[/latex]
- [latex]3102313444_{\text{five}}[/latex]
Answer true or false. If false, explain why
- [latex]2_{\text{four}} = 2[/latex]
- [latex]3_{\text{four}} = 3_{\text{twelve}}[/latex]
- [latex]10_{\text{twelve}} = 10_{\text{five}}[/latex]
Using Base Three blocks, you had 7 flats, 10 longs and 5 units. What number does this represent in
- Base Three?
- Base Ten?
Write each number shown in expanded notation as a numeral in the base specified.
- [latex]3 \times 7^{8} + 6 \times 7^{5} + 4 \times 7^{4}[/latex] to Base Seven
- [latex]1 \times 3^{10} + 2 \times 3^{9} + 2 \times 3^{3}[/latex] to Base Three
Write each number in expanded notation:
- [latex]200050030000_{\text{nine}}[/latex]
- [latex]1 000100001000_{\text{two}}[/latex]
Write each numeral in expanded form. Then, convert each numeral to a Base Ten mixed numeral with the fraction simplified.
- [latex]43.3_{\text{nine}}[/latex]
- [latex]35.12_{\text{six}}[/latex]
- [latex]121.21_{\text{three}}[/latex]
- [latex]333.333_{\text{five}}[/latex]
Rewrite from expanded form to a numeral in the appropriate base.
- [latex]3 \times 4^{2} + 2 \times 4^{0} + 3 \times 4^{-1} + 1 \times 4^{-3}[/latex]
- [latex]5 \times 11^{3} + 10 \times 11^{1} + 8 \times 11^{-1} + 1 \times 11^{-2}[/latex]
- [latex]1 \times 2^{2} + 1 \times 2^{0} + 1 \times 2^{-1} + 1 \times 2^{-4}[/latex]
