39 Multiplication and Division
Louisiana State Standards
Standard Number |
Description of Standard |
| 7.NS.2. | Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers. |
| 7.NS.2.a | a. Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as (–1)(–1) = 1 and the rules for multiplying signed numbers. Interpret products of rational numbers by describing real-world contexts. |
| 7.NS.2.b | b. Understand that integers can be divided, provided that the divisor is not zero, and every quotient of integers (with non-zero divisors) is a rational number. If p and q are integers, then –(p/q) = (–p)/q = p/(–q). Interpret quotients of rational numbers by describing real-world contexts. |
| 7.NS.2.c | c. Apply properties of operations as strategies to multiply and divide rational numbers. |
You will need: Positive and Negative Counters (Material Cards 18A and 18B)
Now, we'll explore how to multiply positive and negative numbers using the counters. Let's look again at a definition of multiplication for whole numbers.
Integer Multiplication with Number Lines
Key Takeaway - Muliplication with Repeated Addition and Number Lines
If [latex]m[/latex] and [latex]n[/latex] are whole numbers, then \[m \times n = n + n + n + n + ... + n, \nonumber \] where there are [latex]m[/latex] addends of [latex]n[/latex] in this sum.
Let's use the definition with a number line for the problem 4 × 3. By the definition, we would be computing 3 + 3 + 3 + 3 = 12. If we look at this on a number line, we would "bounce" 3 spaces for a total of 4 times, so again we get 12 as our answer.

We can modify the definition using whole numbers to work with a whole number times an integer. Let's see how this will work for 4 × ¯3. The definition would then tell us to add ¯3 for a total of 4 times giving (¯3) + (¯3) + (¯3) + (¯3) = ¯12. On the number line, we would need to "bounce" to the left 3 spaces for a total of 4 times to end on ¯12.

Exercise 1
Solve the following problems by using number lines.
a. 2 × 4
Solution
By the definition, we are going to hop 4 spaces to the right 2 times.
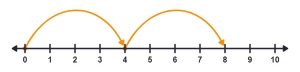
So 2 × 4 = 8
b. 3 × -5
Solution
By the definition we are going to hop 5 spaces to the left 3 times.

So 3 × -5 = -15
When we multiply a whole number times an integer, the process is fairly simple. The first factor (the whole number) tells us how many times we need to hop in the direction of the second factor (the integer). When we reverse the order of the numbers and multiply an integer times a whole number, or even two integers, the process is a little more involved. For these problems, if the first factor is negative, then we will need to reverse the direction of the hops that the second factor would normally go.
Example 1
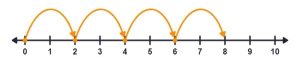
Use a number line to solve -4 × 2.
Solution:
Remember that if we were working with 4 × 2 then we would hop 2 spaces to the right 4 times. However, in this problem we have -4 instead of 4. This means that we need to reverse the direction of the hop and go to the left instead of the right. We're still going to hop 2 spaces 4 times but will go in the opposite direction.
So we can see that -4 × 2 = -8.
Example 2
Use a number line to solve -4 × -2.
Solution:
This time, both factors are negative, so let's see what we need to do. The -2 tells us to hop to spaces to the left. We're still going to hop 4 times, but the negative will flip the direction so we will go to the right instead of the left.
So we can see that -4 × -2 = 8.
Now that you've seen how these work, try a few yourself.
Exercise 2 (solutions)
Solve the following problems by using number lines.
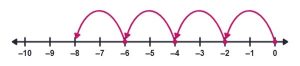
a. -3 × 5
Solution
We need to hop 5 spaces right, but since 3 is negative, then reverse this to hop to the left.

So -3 × 5 = -15
b. -5 × -2
Solution
We need to hop 2 spaces to the left, but since 5 is negative then reverse this to hop to the right.
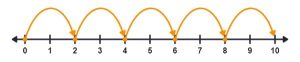
So -5 × -2 = 10
c. 2 × -6
Solution
We need to hop 6 spaces to the left. This time, the 2 is positive, so the direction does not change.
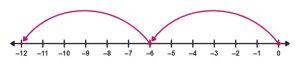
So 2 × -6 = -12
Integer Multiplication with Counters
We're now going to make sense of and modify this definition again using counters as long as m is positive by rewording the definition slightly, as stated below:
If [latex]m[/latex] is a whole number and [latex]n[/latex] is any integer, [latex]m \times n[/latex] is obtained by combining [latex]m[/latex] subsets of a collection of counters representing [latex]n[/latex]. The number that the resulting collection represents is the answer to the problem [latex]m \times n[/latex].
Exercise 3
This exercise shows you one way to use the above definition to multiply 3 × -4. In this problem, the definition can be used because 3 is a whole number and -4 is an integer. We need to combine 3 subsets of a collection of counters that represent -4.
a. Use your positive and negative counters to represent a collection of counters that represent -4. For this exercise, choose a collection of 5 negatives and 1 positive. Show what your collection looks like below:
Solution






b. Now, form two more collections (for a total of 3 subsets) of counters that you had for part a. Combine the counters together and show what the large collection looks like below:
Solution


















After rearranging, we get this collection:


















c. After removing any red-green pairs (zero) from your collection in part b, show the collection that remains below. What number does this represent?
Solution












After removing the red-green pairs, we have 12 red counters or ¯12. So 3 × -4 = -12.
Exercise 4
Do 3 × -4 again, using a different collection of counters to represent -4.
a. Use your positive and negative counters to represent a collection of counters that represent -4. This time, choose a collection of 6 negatives and 2 positives. Show what your collection looks like below:
Solution








b. Now, form two more collections (for a total of 3 subsets) of counters that you had for part a. Combine the counters together and show what the large collection looks like below:
Solution
























After rearranging, we get this collection:
























c. After removing any red-green pairs (zero) from your collection in part b, show the collection that remains below. What number does this represent?
Solution












After removing the red-green pairs, we have 12 red counters or ¯12. So 3 × -4 = -12.
Exercise 5
Okay, let's do 3 × -4 one more time, choosing the easiest way to represent -4.
a. Form a collection of counters to represent -4. Do it the easy, natural way, using the least number of counters possible. Show what your collection looks like below:
Solution




b. Now, form two more collections (for a total of 3 subsets) of counters that you had for part a. Combine the counters together and show what the large collection looks like below:
Solution












After rearranging, we get this collection:












c. What number does the collection in part b represent?
Solution
Since there are no red-green pairs to remove, we just have 12 red counters or ¯12. So 3 × -4 = -12.
Well, I hope you got the answer of -12 for exercises 1, 2, and 3, since 3 × -4 = -12! This illustrates that it doesn't matter exactly which collection of counters you use to represent -4, as long as the collection really is -4. To compute 3 × -4, you could combine 3 subsets of a collection of 8 reds and 4 greens, or you could combine 3 subsets of a collection of 7 reds and 3 greens, etc. You'll always end up with a collection that represents -12. For exercise 3, did you choose 4 negatives as your representation? If so, did you notice you didn't have to remove any red-green pairs to answer part c? From now on, let's do it the easy way, using the simplest collection possible.
Example 3
Use your counters to do each of the following multiplication problem using the definition of multiplying a whole number by an integer. Then, explain what the multiplication problem given means in terms of the counters, and explain and show the individual steps. Use the following example as a model.
Multiply 2 × -6
Solution:
Multiplying 2 × -6 means to combine 2 subsets of 6 red counters. The number that the resulting collection represents is the product (answer).
2 × -6 =












which gives us 12 red counters or -12. So 2 × -6 = - 12.
Exercise 6
Use your counters to do each of the following multiplication problems using the definition of multiplying a whole number by an integer. Then, explain what the multiplication problem given means in terms of the counters, and explain and show the individual steps.
a. Multiply 4 × -2
Solution
Multiplying 4 × -2 means to combine 4 subsets of 2 red counters.








So 4 × -2 = -8.
b. Multiply 3 × 5
Solution
Multiplying 3 × 5 means to combine 3 subsets of 5 green counters.















So 3 × 5 = 15.
c. Multiply 5 × -3
Solution
Multiplying 5 × -3 means to combine 5 subsets of 3 red counters.















So 5 × -3 = -15.
d. Multiply 7 × 2
Solution
Multiplying 7 × 2 means to combine 7 subsets of 2 green counters.














So 7 × 2 = 14.
e. Multiply 0 × -3
Solution
Multiplying 0 × -3 means to combine 0 subsets of 3 red counters. However, since we have no subsets, we have no red counters. This means that 0 × -3 = 0.
Counter Multiplication with Two Integers
Okay, now that you've mastered how to multiply a whole number by an integer, let's work on how we can use the counters to multiply a negative integer by an integer. Let's look once more at the definition for multiplying [latex]m \times n[/latex], when m is a whole number.
If m is a whole number and n is any integer, [latex]m \times n[/latex] is obtained by combining m subsets of a collection of counters representing n. The number that the resulting collection represents is the answer to the problem [latex]m \times n[/latex].
If m is negative, this definition for the multiplication of a whole number times an integer doesn't make sense since you certainly can't combine a negative number of subsets! The way we'll revise this definition to include the possibility that m may be negative is to agree that if m is negative, we REMOVE [latex]m[/latex] subsets of a collection of counters representing [latex]n[/latex]. The trick to doing this is to remove the subsets from a collection of counters representing zero. So, here is the comprehensive definition for multiplying any two integers, using positive and negative counters.
Let's use positive and negative counters to illustrate two cases.
- Case 1: If [latex]m[/latex] is a whole number and [latex]n[/latex] is any integer, [latex]m \times n[/latex] is obtained by combining [latex]m[/latex] subsets of a collection of counters representing [latex]n[/latex]. The product of m and [latex]n[/latex], [latex]m \times n[/latex], is the number that the resulting collection represents.
- Case 2: If [latex]m[/latex] is negative and [latex]n[/latex] is any integer, [latex]m \times n[/latex] is obtained by removing |m| subsets of a collection of counters representing [latex]n[/latex] from a collection of counters representing zero. The product of [latex]m[/latex] and [latex]n[/latex], [latex]m \times n[/latex], is the number that the resulting collection represents.
This exercise below shows you how to use the above definition to multiply [latex]-4 \times 3[/latex]. For this problem, we need to remove 4 subsets of a collection of counters that represent 3 from a collection of counters representing zero. The simplest collection to represent 3 is 3 positives, or 3 green counters. (We could use a more complicated collection and still arrive at the same answer. Convince yourself it wouldn't matter here, either.)
Exercise 7
Using your counters, multiply -4 × 3.
a. We first need to form a collection of counters that represents zero so that it will be possible to remove 4 subsets of 3 green counters. For this example, make a collection of 14 red and 14 green counters. Write down what your collection looks like here:
Solution




























b. From your collection, remove a subset of 3 green counters. Then, remove 3 more subsets of 3 green counters. You have just removed 4 subsets of 3 green counters from zero. To show it on paper, circle a subset of 3 green counters in the collection above in part a. Then, circle 3 more subsets of 3 green counters so that four separate subsets are circled. After you remove the counters (which are shown by what you circled in part a), show what is left in your collection below.
Solution




























(You can see above that 3 green counters have been separated at a time, giving 4 subsets and 2 extra green counters.)
Now we can remove these 4 subsets of green counters.
















c. Remove any red-green pairs (zero) from your remaining collection. Show this on paper by crossing off or circling any red-green pairs (zero) from your collection shown in part b. Show the collection that remains below. What number does this collection of counters represent?
Solution












After removing the red-green pairs, we have 12 red counters or -12. So, -4 × 3 = -12.
Exercise 8
Use the definition again to multiply -4 × 3. Remember, you need to remove 4 subsets of a collection of counters that represent 3.
a. We first need to form a collection of counters that represents zero so that it will be possible to remove 4 subsets of 3 green counters. This time, put in the smallest collection of counters possible so that you'll be able to remove 4 subsets of 3 green counters. Write down what your collection looks like here:
Solution
























b. From your collection, remove four subsets of 3 green counters (take out one subset of 3 green counters at a time). You have just removed 4 subsets of 3 green counters from zero. To show it on paper, circle 4 different subsets of 3 green counters in the collection shown in part a. After you remove the counters (which are shown by what you circled in part a), show what is left in your collection below.
Solution
























You can see above that 3 green counters have been separated at a time, giving 4 subsets of green counters.
After removing the 4 subsets, we get the following:












c. What number does the above collection represent?
Solution
Since there are no red-green pairs to remove, we have 12 red counters or -12 remaining. So, -4 × 3 = -12.
Teaching Tip: Did you notice that if you start out with a minimal collection to represent zero, you don't have to remove any red-green pairs when you get to part c? That is the easiest way to do it because you know how to calculate what to take out before you start the problem. However, if you were teaching this to someone who couldn't figure that out ahead of time, you might always start out with zero being 20 (or some other agreed-upon number) of each counter.
The steps are shown for the example below– how to use your counters to do a multiplication problem when the first number is a negative integer. It's necessary to explain what the multiplication problem given means in terms of the counters, and then explain and show the individual steps. Use the example as a model for the exercises that follow.
Example 4
Multiply -4 × -3 by using the definition of multiplying integers.
Solution:
Multiplying -4 × -3 means to remove 4 subsets of 3 red counters from a representation of zero. The number that the resulting collection represents is the answer.
Step 1: Start with a representation of zero: 12 reds and 12 greens.
























Step 2: Remove 4 subsets of 3 red counters from the above collection. (I've separated the 4 subsets I'm removing.)
























Step 3: Determine what number is represented by what is left in the collection. (Depending on what you used for your original collection for zero, you may have to remove red-green pairs first, and then count the number of counters of one color that remain.) The final collection is:












Since there are 12 greens remaining, the answer is +12. Didn't you always wonder why a negative number times a negative number equaled a positive number? Using the definition of multiplying integers with counters, you can really see why it's true.
Now that we've seen how to multiply integers, we can look at the properties that hold for multiplication.
Key Takeaway - Properties of Multiplication
Just like with addition of integers, the properties for multiplication also hold for integers.
If “a”, “b”, and “c” are integers:
1. Commutative a × b = b × a
2. Associative (a × b) × c = a × (b × c)
3. Identity a × 0 = a = 0 × a
It's time for you to work on a few problems. Some have negative numbers before the multiplication sign (start with a representation of zero and remove subsets as in the last example), and some have whole numbers before the multiplication sign (so just combine subsets together like you did in the earlier exercises of this exercise set). It's the number before the multiplication sign that will indicate which case of the definition you will use.
Exercise 9
Use your counters to do each of the following multiplication problems using the definition of multiplying two integers with positive and negative counters. Then, explain what the multiplication problem given means in terms of the counters, and explain and show each of the individual steps. Use the example above as a model when the first number is negative.
a. -5 × 3
Show work and all steps below. Then, state the answer to the problem.
Solution
Start with a representation of zero that allows you to remove 5 sets of 3 positive counters:






























Remove the 5 sets of 3 positive counters.















Since there are 5 sets of 3 negative counters (or 15 negative counters), the answer is -15.
b. -3 × 2
Show work and all steps below. Then, state the answer to the problem.
Solution
Start with a representation of zero that allows you to remove 3 sets of 2 positive counters:












Remove the 3 sets of 2 positive counters.






Since there are 3 sets of 2 negative counters (or 6 negative counters), the answer is -6.
c. 2 × -3
Show work and all steps below. Then, state the answer to the problem.
Solution
Add 2 sets of 3 negative counters.






Since there are 6 negative counters, the answer is -6.
NOTE: Although the answer to part b is the same as part c due to the commutative property of multiplication, the problems mean different things, the steps are not alike, and the problems are done differently.
d. -2 × 3
Show work and all steps below. Then, state the answer to the problem.
Solution
Start with a representation of zero that allows you to remove 2 sets of 3 negative counters:












Remove the 2 sets of 3 negative counters.






Since there are 6 positive counters, the answer is 6.
e. 3 × 2
Show work and all steps below. Then, state the answer to the problem.
Solution
Add 3 sets of 2 positive counters.






Since there are 6 positive counters, the answer is 6.
f. 0 × - 4
Show work and all steps below. Then, state the answer to the problem.
Solution
Add 0 sets of 4 negative counters. Since there are no counters to add, the answer is 0.
g. -4 × 0 (this means something different than 0 × -4)
Show work and all steps below. Then, state the answer to the problem.
Solution
We need to start with a representation of 0 counters. Since there are no counters to remove, the answer is 0.
Let's do some more problems when the first integer is negative, using a chart to keep track of the counters. The first column will be the multiplication problem, the second will show what representation of zero is being used, the third will explain the meaning of the multiplication problem (what has to be done in all of these cases, subsets are being removed from the representation of zero), the fourth will show how many of each of the counters are left after the removal of the subsets, and the last column will be the answer, obtained from the representation shown in the fourth column.
Exercise 10
Fill in all of the blanks. FILL IN THE ENTIRE TABLE ALL THE WAY TO THE BOTTOM!! You should be using your real manipulatives (red and green counters) as you do (most of) these problems. I've done the first one for you to use as a model.
| Problem | Counters for zero | The meaning of the problem | Counters remaining | Answer |
| -3 × 6 | 20G and 20R | remove 3 sets of 6G from zero | 2G and 20R | -18 |
| -3 × 6 | 23G and 23R | |||
| -3 × 6 | 18G and 18R | |||
| -4 × 4 | 18G and 18R | |||
| -4 × -4 | 18G and 18R | |||
| -5 × 2 | 14G and 14R | |||
| -2 × 5 | 13G and 13R | |||
| -5 × -2 | 11G and 11R | |||
| -2 × -5 | ||||
| -3 × 3 | 10G and 10R | |||
| -3 × -3 | 12G and 12R | |||
| -7 × 2 | ||||
| -2 × 8 | 18G and 18R | |||
| -2 × -8 | 18G and 18R |
After doing all of the exercises in this Exercise Set, the rule for multiplication of integers should make sense.
Solution
| Problem | Counters for zero | The meaning of the problem | Counters remaining | Answer |
| -3 × 6 | 20G and 20R | remove 3 sets of 6G from zero | 2G and 20R | -18 |
| -3 × 6 | 23G and 23R | remove 3 sets of 6G from zero | 5G and 23R | -18 |
| -3 × 6 | 18G and 18R | remove 3 sets of 6G from zero | 18R | -18 |
| -4 × 4 | 18G and 18R | remove 4 sets of 4G from zero | 2G and 18R | -16 |
| -4 × -4 | 18G and 18R | remove 4 sets of 4R from zero | 18G and 2R | 16 |
| -5 × 2 | 14G and 14R | remove 5 sets of 2G from zero | 4G and 14R | -10 |
| -2 × 5 | 13G and 13R | remove 2 sets of 5G from zero | 3G and 13R | -10 |
| -5 × -2 | 11G and 11R | remove 5 sets of 2R from zero | 11G and 1R | 10 |
| -2 × -5 | * 11G and 11R | * remove 2 sets of 5R from zero | * 11G and 1R | 10 |
| -3 × 3 | 10G and 10R | remove 3 sets of 3G from zero | 1G and 10R | -9 |
| -3 × -3 | 12G and 12R | remove 3 sets of 3R from zero | 12G and 3R | -9 |
| -7 × 2 | * 15G and 15R | * remove 7 sets of 2G from zero | * 1G and 15R | -14 |
| -2 × 8 | 18G and 18R | remove 2 sets of 8G from zero | 2G and 18R | -16 |
| -2 × -8 | 18G and 18R | remove 2 sets of 8R from zero | 18G and 2R | 16 |
* answers will vary depending on the counters selected
Key Takeaway - Rules for Multiplying Integers
- To multiply two integers, first multiply the absolute values of the integers. To determine the sign of the product: it is positive if both integers have the same sign (both positive or both negative); otherwise, it is negative (if one of the integers is positive and the other integer is negative). If one of the integers is zero, the answer is zero.
- a × b = ab
- (-a) × (-b) = ab
- a × -b = -(a × b)
- -a × b = -(a × b)
- If you are multiplying more than two integers together, the sign of the product can be determined by how many negative numbers are being multiplied. For every two negative numbers being multiplied together, the answer is positive. Therefore, if there are an even number of negative numbers being multiplied, the sign of the product is positive. If there is an odd number of negative numbers being multiplied, the sign of the product is negative. If one of the integers is zero, the answer is zero.
Exercise 11
Determine if each product is negative (–), positive (+), or zero (0). Do not compute the actual product.
a. (-6)(7)(-5)(-3)(-8)(14)
Solution
Positive - there are 4 negative signs
b. (43)(-47)(99)(87)(-85)(-14)
Solution
Negative - there are 3 negative signs
c. (-61)(-76)(-59)(0)(-84)(-94)
Solution
The solution is zero (0) since we are multiplying by 0. However, if there were no 0 in the problem, the sign would be negative since there are 5 negative signs
d. (-61)(-76)(-59)(-38)(-84)(-94)
Solution
Positive - there are 6 negative signs
Integer Division with Counters
Key Takeaway - Rules for Division of Integers
With multiplication, we saw that multiplying by one negative number gave a negative answer and multiplying by two negative numbers gave a positive answer. Since division can be written as a multiplication problem, the rules apply here as well.
- a ÷ b = c
- (-a) ÷ (-b) = c
- a ÷ (-b) = -c
- (-a) ÷ b = -c
We can show that these rules work by using counters and number lines. We'll look at the counters first, and we'll use the following steps to solve our problems.
- Represent the dividend using the counters.
- Divide the counters into groups based on the divisor.
- If the divisor is negative, flip the counters to the opposite sign.
Example 5
Using the counters, solve -10 ÷ 2.
Solution:
Represent the -10 by using 10 red counters.










Divide the counters into 2 equally sized groups (5 red in each group).










Since the divisor 2 is positive, the counters stay red so the answer is -5.
Example 6
Using the counters, solve 10 ÷ -2.
Solution:
Represent the 10 by using green counters.










Divide the counters into 2 equally sized groups (5 green in each group).










But the divisor is negative, so flip the counters to red.










Since there are now 5 red counters in each group, the answer is -5.
Example 7
Using the counters, solve -10 ÷ -2.
Solution:
Represent the -10 by using red counters.










Divide the counters into 2 equally sized groups (5 red in each group).










But the divisor is negative, so flip the counters to green.










Since there are now 5 green counters in each group, the answer is 5.
As we can see in the last two examples, it's very important to remember to flip the counters when the divisor is negative.
Let's try a few problems to practice this technique.
Exercise 12
Solve the following problems using counters.
a. -12 ÷ 4
Solution
Represent the -12 by using 12 red counters.












Divide the counters into 4 equally sized groups (3 red in each group).












The divisor is positive so the counters stay the same. Since there are 3 red counters in each group, the answer is - 3.
b. 15 ÷ -3
Solution
Represent the 15 by using 15 green counters.















Divide the counters into 3 equally sized groups (5 green in each group).















But the divisor is negative, so flip the counters to red.















Since there are 5 red counters in each group, the answer is -5.
c. -18 ÷ -6
Solution
Represent the -18 by using 18 red counters.


















Divide the counters into 6 equally sized groups (3 counters in each group).


















But the divisor is negative, so flip the counters to green.


















Since there are 3 green counters in each group, the answer is 3.
Integer Division with Number Lines
Now that we've seen how division with counters works, we can see how to use number lines. We'll need to use the following steps to solve our problems.
- The dividend represents the endpoint on the number line.
- The divisor represents the size of the groups used to go from 0 to the endpoint.
- If the divisor is negative, flip the "direction" sign of the endpoint.
- The answer is the number of groups it takes to go from 0 to the endpoint. The sign of the answer is the direction of the hops. (Hops to the right are positive and hops to the left are negative.)
Example 8
Using the number line, solve 10 ÷ 2.
Solution:
Since the dividend is positive 10, mark a number line from at least 0 to at least 10.

The divisor is positive, so "hop" 2 spaces at a time from 0 to 10.
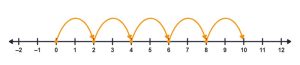
Since it took 5 groups to the right to go from 0 to 10, the answer is 5.
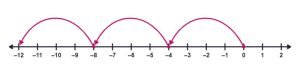
Example 9
Using the number line, solve -10 ÷ 2.
Solution:
Since the dividend is negative 10, mark a number line from at least 0 to at least -10.

The divisor is positive so "hop" 2 spaces at a time from 0 to -10.
Since it took 5 groups to the left to go from 0 to -10, the answer is -5.
Example 10
Using the number line, solve -10 ÷ -2.
Solution:
Since the dividend is negative 10, mark a number line from at least 0 to at least -10.

The divisor is negative, so this will flip the sign on the endpoint. This means that the -10 will become 10.

Now we need to hop 2 spaces at a time from 0 to 10.

Since it took 5 groups to the right to go from 0 to 10, the answer is 5.
Exercise 13
Solve the following problems using number lines.
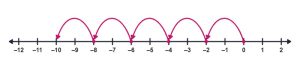
a. -12 ÷ 4
Solution
Since the dividend is negative 12, mark a number line from at least 0 to at least -12.

The divisor is positive, so "hop" 4 spaces at a time from 0 to -12.
Since it took 3 groups to the left to go from 0 to -12, the answer is -3.
b. 15 ÷ -3
Solution
Since the dividend is positive 15, mark a number line from at least 0 to at least 15.

The divisor is negative, so this will flip the sign on the endpoint. This means that the 15 will become -15.

Now hop 3 spaces at a time from 0 to -15.
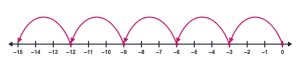
Since it took 5 groups to the left to go from 0 to -15, the answer is -5.
c. -18 ÷ -6
Solution
Since the dividend is negative 18, mark a number line from at least 0 to at least -18.

The divisor is negative, so this will flip the sign on the endpoint. This means that the -18 will become 18.

Now hop 6 spaces at a time from 0 to 18.

Since it took 3 groups to the right to go from 0 to 18, the answer is 3.
Now that you've mastered multiplication and division with integers, let's explore a few more properties.
Closure and Ordering Integers
Remember that for a set to be closed under multiplication, the product of any two elements in the set must be in the set. To prove a set is not closed under multiplication, you need to provide a counterexample.
Exercise 14
For each of the following sets, determine if the set is closed under multiplication. Provide a counterexample if it is not closed.
a.
Solution
The set of integers is closed under multiplication. If you multiply two positive integers, the result is a positive integer. If two negative integers are multiplied, the result is also a positive integer. If a positive integer is multiplied by a negative integer, then the result is a negative integer. In all of these examples, the result is always an integer.
b.
Solution
The set of positive integers is closed under multiplication since the product of any two positive integers is a positive integer.
c.
Solution
The set of negative integers is not closed under multiplication since the product of any two negative integers is a positive integer.
Let's use the example -2 × -3 to prove this.
-2 × -3 = 6 by the rules of multiplication of integers. Since 6 is not in the set of negative integers, then the set is not closed.
d.
Solution
The set {-1, 0} is not closed. If we used the example -1 × -1 we will get an answer of 1. Since 1 is not in the set, the set is not closed under multiplication.
e.
Solution
The set {-1, 1} is closed under multiplication. When we look at the possible products, we see that 1 × 1 = 1, -1 × -1 = 1, and 1 × -1 = -1. These products are elements in the set, so the set is closed.
f.
Solution
The set {-1, 0, 1} is closed under multiplication. Since the only possible products are -1, 0 and 1, then the set is closed.
Less than (<) and Greater than (>) signs are used to order numbers. ([latex]a < b[/latex] if [latex]a[/latex] is to the left of [latex]b[/latex] on the number line. [latex]a < b[/latex] (read "a is less than b") can also be written as [latex]b > a[/latex] (read "b is greater than a.)
Exercise 15
Decide which of the following are true if a, b and c are any integers, p is a positive integer and n is a negative integer. Provide a counterexample if it is false.
a.
Solution
Let's look at the following example to show why this is true.
1 < 2 and 2 < 3 are both true statements.
We know that 1 is less than 3 so the statement that 1 < 3 is also true and then a < b and b < c, so a < c is true.
b.
Solution
Let's use the example 1 < 3 to show why this is true.
We can use any positive integer to show this, but we'll use 2 for this example.
Now 1 + 2 = 3 and 3 + 2 = 5. Since 3 is less than 5, then 1 + 2 < 3 + 2 or a + c < b + c must be true.
c.
Solution
Let's show why is is true by using the example 2 < 5.
We can use any positive integer to prove this property, but we'll use 3 for this example.
Now 2 × 3 = 6 and 5 × 3 = 15. Since 6 is less than 15, then 2 × 3 < 5 × 3 or ap < bp must be true.
d.
Solution
We saw in part c. that multiplying by a positive integer does not change the sign of the inequality. In other words, if a is less than b then multiplying them both by the same positive integer p will make ap < bp.
e.
Solution
Let's use the example 2 < 5 to show why this is true.
We can use any negative integer to prove this, but we'll use -3 for this example.
Now 2 × -3 = -6 and 5 × -3 = 15. In this case, -15 is less than -6 or -6 > -15. So this means that 2 × -3 > 5 × -3 or an > bn must be true.
f.
Solution
We saw in part e. that multiplying by a negative integer changes the sign of the inequality. In other words, if a is less than b, then multiplying them both by the same negative integer n will make an > bn.
Exercise 11a, 11b, 11c, and 11e are the four properties of Ordering for Integers. 11a is called the Transitive Property for Less Than. 11b is called the Property of Less Than and Addition. 11c is the Property of Less Than and Multiplication by a Positive 11e. is the Property of Less Than and Multiplication by a Negative. If the less-than symbols in 11a, 11b and 11c were replaced with greater-than symbols, you would have the corresponding properties of greater than. For part 11e, if both signs were switched, you would have the Property of Greater Than and Multiplication by a Negative.
Exercise 12 (solutions/H5P)
Fill in the following properties, if a, b and c are any integers, p is a positive integer and n is a negative integer.
11a,b and c are similar to properties of equality. The difference between equalities and inequalities (whether there is a less than or greater than symbol) if that when both sides of an inequality are multiplied by a negative number, the inequality sign changes direction.
