26 Digital Roots
[LA math standards relevant to this section will be here.]
Digital Root
What is Digital Root?
It’s helpful to understand what is meant by the digital root of a number because they are used in divisibility tests, and are also used for checking arithmetic problem. A digital root of a number is one of these digits: [latex]0[/latex], [latex]1[/latex], [latex]2[/latex], [latex]3[/latex], [latex]4[/latex], [latex]5[/latex], [latex]6[/latex], [latex]7[/latex] or [latex]8[/latex], which is the remainder obtained when the number is divided by [latex]9[/latex]. Recall that the remainder cannot be a number equal to or greater than the divisor, [latex]9[/latex], so the digital root of any whole number would only be one of these digits: [latex]0[/latex], [latex]1[/latex], [latex]2[/latex], [latex]3[/latex], [latex]4[/latex], [latex]5[/latex], [latex]6[/latex], [latex]7[/latex] or [latex]8[/latex], which are the only possible remainders that can be obtained when a number is divided by [latex]9![/latex]
Definition-Digital Root
The digital root of a number is the remainder obtained when the number is divided by [latex]9[/latex].
Calculate digital root using division
According to the definition, to find the digital root for a given number, we can divide it by [latex]9[/latex] and then find the remainder. For example, to find the digital root of [latex]13[/latex], we divide [latex]13[/latex] by [latex]9[/latex] and get the quotient, [latex]1[/latex] with remainder [latex]4[/latex], so the digital root of [latex]13[/latex] is [latex]4[/latex].
Divide each of the following numbers by [latex]9[/latex] to find their digital roots.
| a. 25
|
h. 8
|
| b. 48
|
i. 54
|
| c. 53
|
j. 74
|
| d. 829
|
k. 481
|
| e. 5042
|
l. 936
|
| f. 3455
|
m. 8314
|
| g. 47522
|
n. 647
|
Calculate Digital Root by Adding All the Digits
As shown in Exercise 1, for multi-digit numbers such as those in items d. to n., it is tedious to find digital roots through dividing them by [latex]9[/latex] and then obtaining the remainder. Below is another easier way to find the digital root of a number, especially those with multiple digits, by addition, instead of division by [latex]9[/latex]. .
Step 1: Add the individual digits of the number.
Step 2: If there is more than one digit after adding all the digits, repeat this process until you get a single digit. If this final sum is a number not equal to [latex]9[/latex], then it is the digital root. If the final sum is [latex]9[/latex], then the digital root is [latex]0[/latex]. In other words, The single digit you finally end up with indicates the DIGITAL ROOT of the number.
Examples 1-6
Find the digital roots of the following numbers.
1. [latex]34[/latex]
Step 1 Add the digits: [latex]3 + 4 = 7[/latex]
Step 2 The sum of the digits is a single digit number not equal to [latex]9[/latex], so the digit root of [latex]34[/latex] is [latex]7[/latex].
Double check: [latex]34 / 9 = 3 R 7[/latex].
2. [latex]321[/latex]
Step 1 Add the digits: [latex]3 + 2 + 1 = 6[/latex]
Step 2 The sum of the digits is a single digit number not equal to [latex]9[/latex], so the digit root of [latex]321[/latex] is [latex]6[/latex].
3. [latex]58[/latex]
Add the digits: [latex]5 + 8 = 13[/latex].
Add the digits again: [latex]1 + 3 = 4[/latex].
The digital root of [latex]58[/latex] is [latex]4[/latex].
4. [latex]97[/latex]
Add the digits: [latex]9 + 7 = 16[/latex] Add the digits again: [latex]1 + 6 = 7[/latex]
The digital root of [latex]97[/latex]is [latex]7[/latex].
5. [latex]72[/latex]
Add the digits: [latex]7 + 2 = 9[/latex] In digital roots, [latex]9[/latex] is the same as [latex]0[/latex]
The digital root of 72 is [latex]0[/latex].
6. 346,721
Add the digits, we get [latex]3 + 4 + 6 + 7 + 2 + 1 = 23[/latex]
Add the digits again: [latex]2 + 3 = 5[/latex]
The digital root of [latex]346,721[/latex] is [latex]5[/latex]
This way of fining digit roots of given numbers is much more enjoyable than dividing them by [latex]9[/latex], because here we are only doing the addition of single digit numbers! You probably wonder why this may work for us. In fact, this seemingly miraculous method is provable using the knowledge of place value. You can find the brief proof below if you are curious about it.
Proof
Let’s take a three-digit number as an example.
Assume abc is a [latex]3[/latex]-digit number with [latex]a[/latex] on the hundreds place, [latex]b[/latex] the tens, and [latex]c[/latex] the ones.
Then
[latex]abc = 100a + 10b + c = 99a + a + 9b + b + c = (99a + 9b) + a + b + c[/latex].
The first part is divisible by [latex]9[/latex] and the remainder of “[latex]abc[/latex]” should be the same as that of ([latex]a+b+c[/latex]), which means, the digital root of “[latex]abc[/latex]” is the same as that of the sum of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex].
Note that, when you work on the steps above to find digital root for a number, be very careful with your writing. Take the number [latex]97[/latex] as an example: you should NOT write the process as “[latex]97 = 16 = 7[/latex]“, because [latex]97[/latex] IS NOT EQUAL to [latex]7[/latex]!! It is the digital root of [latex]97[/latex] that is equal to [latex]7[/latex]. We can use dashes, colons or arrows to indicate the digital root deduced from the given number, so your writing should be something like this: [latex]346,721[/latex] [latex]\rightarrow[/latex] [latex]23[/latex] [latex]\rightarrow[/latex] [latex]5[/latex]. Don’t use equal signs!!!
Calculate Digital Root by Casting out Nines
The last method for finding digital roots uses the fact that [latex]9[/latex] and [latex]0[/latex] are equivalent in digital roots. The process of finding digital roots is also called Casting out Nines. When you add the digits, you don’t have to add the digit [latex]9[/latex] or any combination of numbers that add up to [latex]9[/latex] (like [latex]2[/latex] and [latex]7[/latex], or [latex]5[/latex] and [latex]4[/latex], or [latex]2[/latex] and [latex]3[/latex] and [latex]4[/latex], etc.) – you can “cast out” all [latex]9[/latex]‘s. Cross them off; then add the remaining digits together. The following example illustrates how “casting out nines” simplifies the process of finding the digital root of a large number.
Example 7
Find the digital root of [latex]5,624,398[/latex].
Without casting out nines: [latex]5 + 6 + 2 + 4 + 3 + 9 + 8 = 37[/latex]. Add again: [latex]3 + 7 = 10[/latex]. Add again: [latex]1 + 0 = 1[/latex].
Casting out Nines: Since [latex]5[/latex] and [latex]4[/latex] add up to [latex]9[/latex], cross them off: [latex]\not{5},62\not{4},398[/latex]. Since [latex]6[/latex] and [latex]3[/latex] add up to [latex]9[/latex], also cross them off: [latex]\not{5}, \not{6}2\not{4},\not{3}98[/latex]. Also cross off the [latex]9[/latex]: [latex]\not{5},\not{6}2\not{4},\not{3}\not{9}8[/latex]. The only digits to add are the [latex]2[/latex] and [latex]8[/latex], which is [latex]10[/latex]. The digital root of [latex]10[/latex] is [latex]1[/latex]. So [latex]1[/latex] is the digital root of [latex]5,624,398[/latex] which is the same answer obtained without first casting out nines.
Below, the digital roots for examples [latex]4, 5[/latex] and [latex]6[/latex] on the previous page is computed again using casting out nines. Note that the digital root remains the same.
Rework Examples 4-6 using Casting out Nines
4. [latex]97[/latex]
Cross off the [latex]9[/latex]. Only the [latex]7[/latex] remains. The digital root is [latex]7[/latex].
5. [latex]72[/latex]
[latex]7 + 2 = 9[/latex], so cross them off. Therefore, the digital root is [latex]0[/latex].
6. [latex]346,721[/latex]
Cross off the [latex]3[/latex] and [latex]6[/latex], and also the [latex]7[/latex] and [latex]2[/latex]. The only digits to add are the [latex]4[/latex] and [latex]1[/latex]. Therefore, the digital root is [latex]5[/latex].
The digit root is an important property of a whole number that helps determine its divisibility by 9 and 3. Regardless of how it is calculated—whether by summing all the digits or using division by 9—the result remains the same. A much simpler method, especially for large numbers like those in Example 6 above, is to first cast out nines and then add the remaining digits. In Exercise 2 below, you can practice calculating digit roots using this approach, and then compare results to Exercise 1.
Exercise 2
Find the digital roots of the following numbers, using either method. Remember that [latex]9[/latex] is not a digital root. Write zero ([latex]0[/latex]) if the sum is [latex]9[/latex] (cast out the [latex]9[/latex]).
a. 25
Solution
No nines to cast out.
Add the digits, and the sum 2+5=7 is less than 9.
So, the digital root of 25 is 7.
b. 48
Solution
No nines to cast out.
Add the digits, and the sum 4+8=12 is greater than 9.
Add the digits of 12, and the sum 1+2=3 is less than 9.
So, the digital root of 48 is 3.
c. 53
Solution
No nines to cast out.
Add the digits, and the sum 5+3=8 is less than 9.
So, the digital root of 53 is 8.
d. 829
Solution
Cast out the third digit 9.
Add the rest digits, 8+2=10 is greater than 9.
Then add the digits in “10”, 1+0=1 is less than 9.
So, the digital root of 829 is 1.
e. 5042
Solution
Cast out the digits 5 and 4 because they make a 9.
Add the rest digits, 0+2=2 is less than 9.
So, the digital root of 5042 is 2.
f. 3455
Solution
Cast out the digits 4 and 5 because they make a 9.
Add the rest digits, 3+5=8 is less than 9.
So, the digital root of 3455 is 8.
Solution
Cast out the digits 4 and 5 because they make a 9. Then cast out the digits 7 and 2 because they also make a 9.
The only digit rest is 2.
So, the digital root of 47522 is 2.
h. 8
Solution
This number has only one digit less than 9, so its digital root is itself, 8.
i. 54
Solution
If we cast out 5 and 4 because their sum is 9, there is no digit left. Then the digital root is 0.
j. 74
Solution
No 9s to cast out.
Add the digits, the sum 7+4=11 is greater than 9.
Add the digits in 11, the sum 1+1=2 is less than 9.
So the digital root is 2.
k. 481
Solution
Cast out the two digits 8 and 1.
The only digit left is 4.
So, the digital root of 481 is 4.
l. 936
Solution
Cast out 9, and 3 with 6.
There is no digit left. Then the digital root is 0.
m. 8314
Solution
Cast out the two digits 8 and 1.
The digits left are 3 and 4. 3+4=7 is less than 9.
So, the digital root of 8314 is 7.
n. 647
Solution
No 9s to cast out.
Add the digits, 6+4+7=17 and the sum is greater than 9.
Add the digits in 17, 1+7=8.
So, the digital root of 647 is 8.
Using Digital Roots is to Check Whole Number Operation Problems.
Check Addition Problems
We can use digital roots to check arithmetic problems using the property of digital roots stated below:
The digital root of the sum of two numbers is equal to the sum of the digital roots of these two numbers.
For example, the digital root of 311 is 5, and the digit root of 129 is 3, then the digital root of the sum 311+129 should be 5+3=8. We may calculate the sum 311+129=440 and find out its digital root is indeed 4+4=8. We may describe this using math language as below:
Digital Root (311+129) = Digital Root (311) + Digit Root (129)
Notice that it is possible for the sum of two digital roots being greater than 9. In this case we can find the digital root of the sum of the two digital roots, it will still be equal to the digital root of the sum.
Let’s consider the sum 3867+485=4352.
Digital root of the sum 4352 is 5 but Digital Root (3867)=6 and Digital Root (485)=8. In this case, the sum of the digital roots of the two addends, 6+8=14>9, cannot literally be equal to the digital root of the sum, which must be a whole number less than 9. However, if we consider the digital root of the sum 14, we find out that Digital Root (14)= 5, which is exactly the digital root of the sum 4352.
If we use arrows to indicate digital roots of numbers, we may write the discussion above as below:
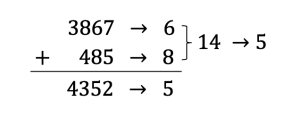
The digital root at the end of the chain above for the two addends is equal to the digit root of the sum, which indicates that the addition is calculated correctly. In summary, to check an addition problem, add the digital roots of the addends. Then, check to see if the digital root of that sum is the same as the digital root of the actual sum of the addends. This works whether there are only two addends, or several addends.
Below are some examples of how to check addition. The actual addition is shown to the left. Arrows are used to show the digital roots of the addends and sum. To check, the digital roots of the addends are added together, and then the digital root of that sum is computed. Compare it to the digital root of the actual sum. If they are equal, put a check to indicate the answer is probably correct.
NOTE: There is a slight chance that the digital roots match, but the answer is still not correct due to some other mistake, like transposing digits. For instance, in example 1 below, it’s possible someone might write down [latex]1153[/latex] for the answer. The digital roots in the check would match. The possibility of this happening is slight, so we generally assume the problem was done correctly if the digital roots check. On the other hand, if the digital roots do not check, you know for sure that it is wrong.
Check if the addition is correct using digital roots.
i. [latex]723+412=1135[/latex]
Solution:
The digit roots of the addends: 723 -> 3, 412 -> 7, and 3+7=10 ->1.
The digit root of the sum: 1135 -> 10 ->1, which equals the sum of the digital roots.
Therefore, it is very likely that the addition problem was done correctly.
ii. [latex]463+529=1630[/latex]
Solution:
The digit roots of the addends: 463 -> 4, 529 -> 7, and 4+7=11->2.
The digit root of the sum: 1630->1.
Therefore, the addition problem was done incorrectly.
You may write the two examples as below:
[two figures with the addition written in columns.]
Someone did the following addition problems, but only wrote down the answers. Check the answer to each problem by using digital roots. Note that the procedure is the same if there are more than two addends. Add the digital roots of all the addends. Show all work
a.
|
[latex]4983[/latex] [latex]\underline {+6829}[/latex] |
| [latex]10802[/latex] |
b.
|
[latex]5567[/latex] [latex]\underline {+ 4987}[/latex] |
| [latex]10554[/latex] |
c.
|
[latex]3467[/latex] [latex]\underline {+ 2541}[/latex] |
| [latex]5908[/latex] |
d.
|
[latex] 8972[/latex] [latex]8876[/latex] [latex]\underline{+ 5873}[/latex] |
| [latex] 23721[/latex] |
e.
|
[latex]5873[/latex] [latex]3674[/latex] [latex]\underline{+ 4763}[/latex] |
| [latex]13260[/latex] |
f.
|
[latex]4789[/latex] [latex]9835[/latex] [latex]\underline{+ 5301}[/latex] |
| [latex] 19925[/latex] |
Check Multiplication Problems
For a multiplication problem, the check is similar, except to check, you multiply the digital roots of the numbers you are multiplying. To check addition, you ADD the digital roots of the addends and check against the digital root of the sum. To check multiplication, you MULTIPLY the digital root of the numbers being multiplied and check against the digital root of the product. Here are some examples that provide an answer someone might have written down after doing the multiplication problem on another piece of paper.
Example 9
i. Is “[latex]85 \times 63 = 5355[/latex]” correct?
Solution:
[latex]85 \rightarrow 13[/latex] [latex]\rightarrow 4[/latex]
[latex]\underline{\times 63} \rightarrow 0[/latex]
[latex]5355 \rightarrow 18 \rightarrow 0[/latex]
Check: [latex]4 \times 0 = 0[/latex]. Correct!
Explanation: To check, multiply the digital roots of the numbers you are multiplying ([latex]4 \times 0 = 0[/latex]); then find the digital root of [latex]0[/latex] ([latex]0[/latex]). Verify that it equals the digital root of the product, [latex]5355[/latex] ([latex]0[/latex]). Since it does, the multiplication problem was probably done correctly.
ii. Is “[latex]43 \times 52 = 2136[/latex]” correct?
Solution:
[latex]43 \rightarrow 7[/latex]
[latex]\underline{\times 52} \rightarrow 7[/latex]
[latex]2136 \rightarrow 3[/latex]
Check: [latex]7 \times 7 = 49 \rightarrow 4[/latex]. Incorrect!
Explanation: To check, multiply the digital roots of the numbers you are multiplying ([latex]7 \times 7 = 49[/latex]); then find the digital root of [latex]49[/latex] ([latex]4[/latex]). This should equal the digital root of the product, [latex]2136[/latex] ([latex]3[/latex]). Since it doesn’t , there is a mistake. Therefore, the multiplication problem was done incorrectly.
Exercise 4
Someone did the following multiplication problems, but only wrote down the answers. Check the answer to each problem by using digital roots. Show Work!
| a.
[latex]74[/latex] [latex]\underline{\times 53}[/latex] [latex]3922[/latex]
|
b.
[latex]29[/latex] [latex]\underline{\times 36}[/latex] [latex]944[/latex]
|
c.
[latex]68[/latex] [latex]\underline{\times 28}[/latex] [latex]1904[/latex]
|
|||
| d.
[latex]65[/latex] [latex]\underline{\times 79}[/latex] [latex]5125[/latex]
|
e.
[latex]81[/latex] [latex]\underline{\times 55}[/latex] [latex]4455[/latex]
|
f.
[latex]48[/latex] [latex]\underline{\times 52}[/latex] [latex]2596[/latex]
|
|||
| g.
[latex]569[/latex] [latex]\underline{\times 61}[/latex] [latex]34709[/latex]
|
h.
[latex]653[/latex] [latex]\underline{\times 524}[/latex] [latex]242172[/latex]
|
i.
[latex]2333[/latex] [latex]\underline{\times 1203}[/latex] [latex]2806599[/latex]
|
Below is a set of exercise including both addition and multiplication.
Exercise 5
Add or multiply the following as indicated, then use digital roots to check the answer to each problem. Show Work!
| a.
[latex]7362[/latex] [latex]\underline{+ 5732}[/latex]
|
b.
[latex]8308[/latex] [latex]\underline{+ 956}[/latex]
|
||||
| c.
[latex]6784[/latex] [latex]\underline{+ 6835}[/latex]
|
d.
[latex]9994[/latex] [latex]\underline{+ 8721}[/latex]
|
||||
| e.
[latex]57[/latex] [latex]\underline{\times 8}[/latex]
|
f.
[latex]34[/latex] [latex]\underline{\times 7}[/latex]
|
||||
| g.
[latex]87[/latex] [latex]\underline{\times 52}[/latex]
|
h.
[latex]825[/latex] [latex]\underline{\times 13}[/latex]
|
Check Subtraction Problems.
To check subtraction, you usually add the difference (the answer) to the subtrahend (the number that was subtracted) and see if you get the minuend (the number you subtracted from). That is, to check that[latex]215 – 134 = 81[/latex] was done correctly, simply add [latex]81[/latex] and [latex]134[/latex], which is [latex]215[/latex]. Therefore, to check subtraction using digital roots, simply add the digital root of the difference to the digital root of the subtrahend and see if you get the digital root of the minuend.
For example, to check that [latex]215 – 134 = 81[/latex] was done correctly, simply add the digital roots [latex]81[/latex] and[latex]134: 0 + 8 = 8[/latex]. Verify that [latex]8[/latex] is the digital root of the minuend, [latex]215[/latex]. It is!
Here is another example. Let’s say someone did the following subtraction problem: [latex]5462 – 2873 = 2589[/latex]. To check, add the digital roots of [latex]2589[/latex] and [latex]2873[/latex], or [latex]6 + 2[/latex] to get [latex]8[/latex]. Since [latex]8[/latex] is also the digital root of [latex]5462[/latex], the answer is probably correct.
Here are some more examples of how to check subtraction using digital roots.
Example 10
i. Is “[latex]7362-5732=1630[/latex]” correct?
Solution:
[latex]7362 \rightarrow 0[/latex]
[latex]\underline{ – 5732} \rightarrow 8 [/latex]
[latex]1630 \rightarrow 1[/latex]
Check: [latex]1 + 8 = 9 \rightarrow 0[/latex], which is the digital root of the subtrahend. Correct!
Explanation: To check, add the digital root of the difference and subtrahend ([latex]1 + 8 = 9[/latex]). The digital root of [latex]9[/latex]is [latex]0[/latex]. Verify that this equals the digital root of the minuend, [latex]7632[/latex]([latex]0[/latex]). Since it does, the subtraction was probably done correctly.
ii. Is “[latex]5083-878=4205[/latex]“correct?
Solution:
[latex]5073 \rightarrow 6[/latex]
[latex]\underline{ – 878} \rightarrow 5[/latex]
[latex]4205 \rightarrow 2[/latex]
Check: [latex]2 + 5 = 7[/latex] WRONG!
Explanation: To check, add the digital root of the difference and subtrahend ([latex]2 + 5 = 7[/latex]). This should equal the digital root of the minuend, [latex]5073[/latex] ([latex]6[/latex]). Since it doesn’t, the subtraction was not done correctly.
Below are more exercises on checking subtraction using digital roots.
Exercise 6
Someone did the following subtractions problems, but only wrote down the answers. Check the answer to each problem by using digital roots. Show Work!
| a.
[latex]572[/latex] [latex]\underline{-356}[/latex] [latex]216[/latex]
|
b.
[latex]296[/latex] [latex]\underline{-189}[/latex] [latex]107[/latex]
|
c.
[latex]501[/latex] [latex]\underline{-327}[/latex] [latex]284[/latex]
|
|||
| d.
[latex]3217[/latex] [latex]\underline{-2391}[/latex] [latex]926[/latex]
|
e.
[latex]3546[/latex] [latex]\underline{-1138}[/latex] [latex]2408[/latex]
|
f.
[latex]7502[/latex] [latex]\underline{-4729}[/latex] [latex]2773[/latex]
|
The following exercise will help you review the algorithms of addition, subtraction, and multiplication of whole numbers, then practice how to use digital roots to check if they are calculated correctly.
Exercise 7
Subtract, add or multiply the following as indicated, then use digital roots to check the answer to each problem. Show Work!
| a.
[latex]7362[/latex] [latex]\underline{- 5732}[/latex]
|
b.
[latex]8308[/latex] [latex]\underline{- 956}[/latex]
|
||||
| c.
[latex]6784[/latex] [latex]\underline{- 6335}[/latex]
|
d.
[latex]9994[/latex] [latex]\underline{-8721}[/latex]
|
||||
| e.
[latex]557[/latex] [latex]\underline{+ 348}[/latex]
|
f.
[latex]834[/latex] [latex]\underline{+ 767}[/latex]
|
||||
| g.
[latex]48[/latex] [latex]\underline{\times 6}[/latex]
|
h.
[latex]13[/latex] [latex]\underline{\times 29}[/latex]
|
Check Division Problems
In general, to check division, you multiply the divisor (the number you are dividing by) by the quotient (the answer), and then add the remainder. It is correct if the answer obtained is equal to the dividend (the number you divided into).
For example, here is how to check the division [latex]431 \div 34 = 12[/latex][latex]R. 23[/latex]:
Multiply [latex]34[/latex] by [latex]12[/latex]and add [latex]23[/latex]:
[latex]34 \times 12 + 23 = 408 + 23 = 431[/latex].
Since [latex]431[/latex] is the dividend, this problem was done correctly.
To check division using digital roots, simply multiply the digital root of the divisor by the digital root of the quotient, and add the digital root of the remainder. If the digital root of that number equals the digital root of the dividend, it is probably correct.
Note: After the digital roots of the divisor and quotient are multiplied, you can first find the digital root of that product before adding the digital root of the remainder.
Here is how to check the division problem we did above by using digital roots.
Multiply the digital root of the divisor, [latex]34[/latex], by the digital root of the quotient, [latex]12[/latex]:
[latex]7 \times 3 = 21[/latex].
Then add the digital root of the remainder, [latex]23[/latex]:
[latex]21 + 5 = 26[/latex].
Determine the digital root of that number, [latex]26[/latex], which is [latex]8[/latex].
Check to see if [latex]8[/latex] matches the digital root of the dividend, [latex]431[/latex]. It does.
As stated in the note, you could determine the digital root of [latex]21[/latex] before adding the digital root of the remainder. In this case, it would have looked like this:
[latex]7 \times 3 = 21 \rightarrow 3[/latex].
Then add the digital root of the remainder, [latex]23[/latex]: [latex]3 + 5 = 8[/latex].
Verify that this equals the digital root of the dividend, [latex]431[/latex]. It does.
Therefore, the division was probably done correctly.
As the reader may have already noticed, similar to subtraction, the checking of division using digital roots is based on its inverse operation multiplication together with addition. Therefore, we do not provide the examples and exercises specifically for division. The readers interested in this topic can produce their own to check.
One More Note of Caution about Using Digital Roots to Check Operations
The digit 0 in a number will not contribute to its digital root. For example, both 19 and 109 have the same digital root, 1. Therefore, there is a small chance that the answer is incorrect but it would check when we use digital roots. So, you should also check the reasonableness of the answer by approximating. For instance, [latex]78 times 12[/latex] is about 80 times 10 or 800, which is not even close to equaling the dividend, 7988. Another time digital roots might fail is when someone transposes the digits of a number. If the answer to a problem was 465, and it was written as 456, using digital roots wouldn’t detect the mistake.