44 Decimals
Louisiana Student Standards
Standard Number |
Description of Standard |
| 4.NF.C.6 | Use decimal notation for fractions with denominators 10 or 100. For example, rewrite 0.62 as 62/100; describe a length as 0.62 meters; locate 0.62 on a number line diagram; represent 62/100 of a dollar as $0.62. |
| 4.NF.C.7 | Compare two decimals to hundredths by reasoning about their size. Recognize that comparisons are valid only when the two decimals refer to the same whole. Record the results of comparisons with the symbols >, =, or.
|
| 5.NBT.A.1 | Recognize that in a multi-digit number, a digit in one place represents 10 times as much as it represents in the place to its right and 1/10 of what it represents in the place to its left. |
| 5.NBT.A.2 | Explain and apply patterns in the number of zeros of the product when multiplying a number by powers of 10. Explain and apply patterns in the values of the digits in the product or the quotient, when a decimal is multiplied or divided by a power of 10. Use whole-number exponents to denote powers of 10. For example, 100 = 1, 101 = 10 ... and 2.1 x 102 = 210. |
| 5.NBT.A.3 | Read, write, and compare decimals to thousandths. a. Read and write decimals to thousandths using base-ten numerals, number names, and expanded form, e.g., 347.392 = 3 × 100 + 4 × 10 + 7 × 1 + 3 × (1/10) + 9 × (1/100) + 2 × (1/1000). b. Compare two decimals to thousandths based on the meanings of the digits in each place, using >, =, and < symbols to record the results of comparisons. |
| 5.NBT.A.4 | Use place value understanding to round decimals to any place. |
| 5.NBT.B.7 | Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; justify the reasoning used with a written explanation. |
The meaning of decimals is best understood once one has a real understanding of place value and fractions. The decimal notation we commonly use is an extension of place value in base ten. The decimal point indicates that succeeding digits represent tenths, hundredths, thousandths, etc. So a person must understand what these fractions mean in order to understand and make the connection to decimals.
The key to understanding the relationship between decimals and fractions (or mixed numbers) begins with READING the decimal correctly. Most people read 5.3 as "five point three," which doesn't help one understand its meaning. It should be read "five and three tenths." In doing so, the connection between the decimal 5.3 and the mixed number [latex]5 \frac{3}{10}[/latex] is clear. Similarly, 18.035 should be read "Eighteen and thirty-five thousandths" and corresponds to the mixed number [latex]18 \frac{35}{1000}[/latex]. Here are a few more:
- 0.309 and [latex]\frac{309}{1000}[/latex] are both correctly read "three hundred nine thousandths"
- 10.04 and [latex]10 \frac{4}{100}[/latex] are both correctly read "ten and four hundredths"
Note that the decimal point is read as "and". The decimal point (and the word "and") separates the whole part from the fractional part of a mixed number. This is the only correct use of the word "and" when reading numbers. 760 is read "seven hundred sixty." A common mistake is to read 760 as "seven hundred and sixty." If there is no decimal point, don't say the word "and".
People just learning about decimals (like elementary school children) should NOT read the number 5.4 as "five point four". This is a shortcut way of reading the number that is only appropriate to use once one really understands the connection between decimals and fractions. Remember that a number written in decimal form is really just a different way to write a mixed number where the denominator of the fractional part is a power of ten! The name of the fractional part (tenths, hundredths, thousandths, etc.) is the place value of the last digit of the number after the decimal point, which also happens to be the denominator of the number written in fractional form.
Look again at 0.309 and [latex]\frac{309}{1000}[/latex]. In the decimal, there are three digits (or place values) after the decimal point. In the fraction, there are three zeroes after the 1 (which is the number 1000 in the denominator). The same applies to 18.035 and [latex]18 \frac{35}{1000}[/latex]. For 5.3 and [latex]5 \frac{3}{10}[/latex], the decimal has one digit after the decimal point, and the fraction has one zero after the 1. It's best if students are allowed to discover this fact for themselves. It's always more meaningful to discover relationships (that often become rules) on your own. Students who are regularly asked to read decimals, fractions, and mixed numbers the correct way are more likely to make this particular discovery by themselves.
Mixed numbers like 5.3 and 18.035 can also be written immediately as improper fractions. The denominator of the fraction will still be the same as if it were written as a mixed number. The numerator is the number without a decimal point at all. For instance, 5.3 can be written as [latex]5 \frac{3}{10}[/latex] or [latex]\frac{53}{10}[/latex]; and 18.035 can be written as [latex]18 \frac{35}{1000}[/latex] or [latex]\frac{18035}{1000}[/latex].
Note that when you first write a decimal as a fraction, it isn't necessarily in simplest (or reduced) form.
Exercise 1
For the problems below, you'll write the names of the following decimals and the equivalent fractions or equivalent improper fractions and mixed numbers.
a. For 0.4:
b. For 0.26:
c. For 3.08:
d. For 9.85:
e. For 17.305:
In the first exercise, we took a decimal and converted it into a fraction or improper fraction and mixed number by using powers of 10: tenths, hundredths, thousandths, etc. Understanding the relationship between a decimal and a fraction allows us to use the relationship to convert from a fraction to a decimal as well. Each zero in the denominator represents a place for the decimal point.
Exercise 2
Write each proper fraction as a decimal. Write each improper fraction first as a mixed number (don't reduce), and then also as a decimal. Do not use your calculator.
a. [latex]\frac{14}{100}[/latex]
Solution
0.14
b. [latex]\frac{8}{1000}[/latex]
Solution
0.008
c. [latex]\frac{435}{100}[/latex]
Solution
[latex]4 \frac{35}{100}[/latex] or 4.35
d. [latex]\frac{5638}{10}[/latex]
Solution
[latex]563 \frac{8}{10}[/latex] or 563.8
e. [latex]\frac{305}{100}[/latex]
Solution
[latex]3 \frac{5}{100}[/latex] or 3.05
Converting from a fraction with a power of 10 in the denominator to a decimal is fairly easy, just as converting from a decimal to a fraction with a power of 10 in the denominator was in the first exercise. Let's see what happens when we have a fraction that can be reduced after converting or when our beginning fraction has a denominator other than a power of 10.
Example 1
Convert 0.82 and 0.125 to fractions in the simplest/reduced form.
Solution:
Let's start with 0.82. Since there are two decimal places, we know that the denominator will have two zeroes or 100. This gives us the following fraction:
[latex]\frac{82}{100}[/latex]
But, both 82 and 100 are even numbers so they can be reduced down to the following:
[latex]\frac{82}{100}[/latex] = [latex]\frac{41 \times 2}{50 \times 2}[/latex] = [latex]\frac{41}{50}[/latex]
Now let's try 0.125. This time we have three decimal places so this denominator will have three zeroes or 1000. The fraction would then be:
[latex]\frac{125}{1000}[/latex]
Here, both 125 and 1000 are divisible by several powers of 5, so we can reduce it down to:
[latex]\frac{125}{1000}[/latex] = [latex]\frac{1 \times 125}{8 \times 125}[/latex] = [latex]\frac{1}{8}[/latex]
Exercise 3
Convert the following decimals into simplified/reduced fractions. Show all of your work.
a. 0.6
Solution
0.6 is the fraction [latex]\frac{6}{10}[/latex]
Both 6 and 10 are divisible by 2, so the simplified fraction is [latex]\frac{3}{5}[/latex].
b. 0.55
Solution
0.55 is the fraction [latex]\frac{55}{100}[/latex]
Both 55 and 100 are divisible by 5, so the simplified fraction is [latex]\frac{11}{20}[/latex].
c. 0.72
Solution
0.72 is the fraction [latex]\frac{72}{100}[/latex]
Both 72 and 100 are divisible by 4 so the simplified fraction is [latex]\frac{18}{25}[/latex].
d. 0.325
Solution
0.325 is the fraction [latex]\frac{325}{1000}[/latex]
Both 325 and 1000 are divisible by 25, so the simplified fraction is [latex]\frac{13}{40}[/latex].
e. 0.186
Solution
0.186 is the fraction [latex]\frac{186}{1000}[/latex]
Both 186 and 1000 are divisible by 2, so the simplified fraction is [latex]\frac{93}{500}[/latex].
Definition - Terminating and Repeating Decimals
A decimal with a finite number of digits after the decimal point is called a terminating decimal. A decimal with a digit or group of digits that repeat indefinitely is called a repeating decimal. This repeating group of digits is called the repetend and can be represented with three dots (or ellipsis) or a horizontal line (or vinculum) above the repetend.
For example, 0.52 is a terminating decimal since there are only two digits after the decimal point.
Now, we can show a repeating decimal as either 0.131313... or as [latex]0. \overline{13}[/latex].
As you can see, if a fraction is written with a power of ten in the denominator, it's easy to write the same number in decimal form. Any fraction that is written with a power of 10 in the denominator can be written as a terminal decimal. This means that it's possible to write the number with trailing zeroes. But what if the fraction doesn't have a power of 10 (like 10, 100, 1000, etc.) in the denominator?Â
If a fraction WITHOUT a power of ten in the denominator CAN be written as an equivalent fraction WITH a power of ten in the denominator, then it can be written as a terminating decimal.
For instance, [latex]\frac{1}{2}[/latex] can be written as [latex]\frac{5}{10}[/latex] (by multiplying the numerator and denominator by 5)
Therefore, [latex]\frac{1}{2}[/latex] = [latex]\frac{5}{10}[/latex] = 0.5 (remember to read this as five-tenths)
Now, what about [latex]\frac{7}{80}[/latex]? The question is whether you can multiply the denominator, 80, by something to get 10, 100, 1000, 10000, etc. There is no whole number you can multiply 80 by to get 10, 100, or 1000. But, if you multiply 80 times 125, it equals 100000. So, by multiplying both 7 and 80 by 125, we get the equivalent fraction [latex]\frac{875}{10000}[/latex] for [latex]\frac{7}{80}[/latex] which can now be written as the decimal 0.0875.
How about writing [latex]\frac{5}{6}[/latex] as a terminating decimal? Well, there is nothing you can multiply 6 by to get 10 or 100 or 1000, or 10000. Is there maybe some number we could multiply 6 by to get some higher power of ten? Well, that's a good question! Actually, there isn't, but how could you be sure? You certainly can't try every power of ten since there are an infinite number of them to try. In this case, one method that we can use to find the decimal is to divide.
Example 2
Convert the following fractions into decimals. When possible, change the fraction into one with a power of 10 in the denominator. If it's not possible, use division to convert to a fraction.
a. [latex]\frac{4}{5}[/latex]
b. [latex]\frac{2}{3}[/latex]
Solution:
a. [latex]\frac{4}{5}[/latex]
The fraction [latex]\frac{4}{5}[/latex] can be changed into the equivalent fraction [latex]\frac{8}{10}[/latex], which gives us the decimal answer 0.8.
This way was the easiest, but if we didn't recognize the equivalent fraction, then we still could have gotten the answer by using division. The denominator or "whole" is used as the divisor while the numerator or "part" is the dividend. Let's see how this works:
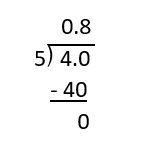
b. [latex]\frac{2}{3}[/latex]For this fraction, changing to an equivalent fraction isn't an option since there is no power of 10 that is divisible by 3. In this case, we need to go directly to division in order to find our decimal.
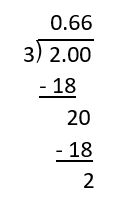We can see here that we're going to keep getting a remainder of 2 no matter how many times we divide. This shows us that we have a repeating decimal, and since the repetend part is the 6, then we can write our answer as: 0.[latex]\overline{6}[/latex]
Exercise 4
Convert the following fractions into decimals. When possible, change the fraction into one with a power of 10 in the denominator. If it's not possible, use division to convert to a fraction.
a. [latex]\frac{7}{20}[/latex]
Solution
[latex]\frac{7}{20} = \frac{35}{100} = 0.35[/latex]
b. [latex]\frac{5}{9}[/latex]
Solution
[latex]\frac{5}{9}[/latex] can't be changed into a fraction with a denominator that has a power of 10, so we need to use division.
Since we have a repeating decimal, we can write it as 0.555... or as [latex]0. \overline{5}[/latex]
c. [latex]\frac{8}{15}[/latex]
Solution
[latex]\frac{8}{15}[/latex] can't be changed into a fraction with a denominator that has a power of 10, so we need to use division.
Since we have a repeating decimal, we can write it as 0.533... or as [latex]0.5 \overline{3}[/latex]
d. [latex]\frac{63}{72}[/latex]
Solution
At first glance, [latex]\frac{63}{72}[/latex] doesn't appear to be a fraction that can be changed to an equivalent fraction with a power of 10 in the denominator. However, it can be simplified.
[latex]\frac{63}{72} = \frac{7}{8}[/latex] and now [latex]\frac{7}{8} = \frac{875}{1000} = 0.875[/latex]
It would be nice if there were an easy way to determine if any given fraction could be written as a terminating decimal. The key is to consider the factors of the denominator of a fraction that can be written as a terminating decimal. If a fraction can be written as a terminating decimal, then there is some equivalent fraction where the denominator must be a power of ten: 10 or 100 or 1000, etc.
Exercise 5
Write the prime factorization of each of the following:
a. 10
Solution
[latex]10 = 2 × 5[/latex]
b. 100
Solution
[latex]100 = 10 × 10 = 2 × 5 × 2 × 5 = 2^2 × 5^2[/latex]
c. 1000
Solution
[latex]1000 = 10 × 10 × 10 = 2 × 5 × 2 × 5 × 2 × 5 = 2^3 × 5^3[/latex]
d. 10000
Solution
[latex]10000 = 10 × 10 × 10 × 10 = 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5 = 2^4 × 5^4[/latex]
e. 100000
Solution
[latex]100000 = 10 × 10 × 10 × 10 × 10 = 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5 = 2^5 × 5^5[/latex]
Hopefully, you can see a pattern occurring here. Powers of ten only have 2s and 5s as its prime factors and nothing else.
Let's go back to our three numbers, [latex]\frac{1}{2}[/latex], [latex]\frac{7}{80}[/latex], and [latex]\frac{5}{6}[/latex], that we were trying to write as terminating decimals and analyze the situation.
[latex]\frac{1}{2}[/latex] is simplified, and in its prime factored form, there is exactly one 2 in the denominator. To write as an equivalent fraction with a denominator that is a power of ten, it must have only 2s and 5s as prime factors in the denominator, and the same number of each! Therefore, multiplying by one more 5 in the numerator and denominator did the trick!
Let's now look at the prime factorization for our next fraction: [latex]\frac{7}{80} = \frac{7}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 5}[/latex]
We must determine if it is possible to multiply the denominator by something so that the resulting denominator will be made up of only 2s and 5s and the same number of each. Well, there are four factors of 2 and one factor of 5. Since we need the same number of each factor, we can make an equivalent fraction by multiplying the numerator and denominator by three more factors of 5.
[latex]\frac{7}{80} = \frac{7}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 5} \cdot \frac{5 \cdot 5 \cdot 5}{5 \cdot 5 \cdot 5} = \frac{875}{10000} = 0.0875[/latex]
In both examples, note that we either multiplied by extra factors of 2 or 5, but not both!
What about [latex]\frac{5}{6}[/latex]? Well, it's reduced, and the prime factorization of the denominator is [latex]2 \cdot 3[/latex]. No matter what the denominator is multiplied by, we'll be stuck with a factor of 3 in the denominator. Since the only prime factors of powers of 10 are 2 and 5, there can't be a prime factor of 3 in the denominator if we want to end up with only a power of 10 in the denominator. Therefore, since it is impossible to write [latex]\frac{5}{6}[/latex] as an equivalent fraction with a power of ten in the denominator, it cannot be written as a terminating decimal.
How about [latex]\frac{63}{72}[/latex]? If we look at the prime factorization for the denominator, we get [latex]2 \cdot 2 \cdot 2 \cdot 3 \cdot 3[/latex]. The threes in the prime factorization should indicate that we will have a repeating decimal, but as we saw earlier in exercise 4, though, [latex]\frac{63}{72}[/latex] is equal to the terminating decimal 0.875. This means that we need to look at more than just the denominator. If we go back and look at the entire fraction again, we'll see that [latex]\frac{63}{72}[/latex] = [latex]\frac{7 \cdot 9}{8 \cdot 9}[/latex] = [latex]\frac{7}{8}[/latex]. Now that we've reduced the fraction down to its simplest form, we do have only 2s in the prime factorization of 8. Since we have three 2s, then we need to multiply three 5s to the numerator and denominator to have a power of 10.
[latex]\frac{7}{80} = \frac{7}{8} \cdot \frac{5 \cdot 5 \cdot 5}{5 \cdot 5 \cdot 5} = \frac{875}{1000} = 0.875[/latex]
Example 3
Convert [latex]\frac{5}{6}[/latex] into a fraction. First determine whether or not this fraction will be terminating or repeating and then use division to find the decimal.
Solution:
First we need to look at the prime factorization of the denominator: [latex]2 \cdot 3[/latex]. Because we have a "3" then this means that we'll have a repeating decimal.
Now we can use division to find the repeating decimal.
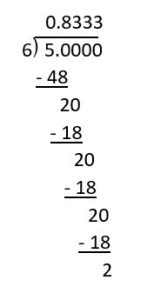
The answer can be written as 0.8333333... or [latex]0.8 \overline{3}[/latex].
One thing to notice about what happened when we divided 5 by 6 is that we kept getting 2 after each subtraction in the division; this is like the remainder. When you divide, each remainder must be less than or equal to what you are dividing by.
Let's now look at what happens when you do long division to compute [latex]\frac{4}{11}[/latex] and [latex]\frac{2}{7}[/latex] and how the statement above applies.
In both of these cases, eventually, you get a remainder that you got previously, so the computation repeats itself. In the case of dividing 4 by 11, two remainders come up before there is some repetition, 4 and 7. In order to have a remainder, you have to have a number less than what you are dividing by; otherwise, you could have used a larger quotient in your division. As an example, let's look at 11. The only possible remainders for 11 are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. Now, if you got a remainder of 0 when dividing, you'd have a terminating decimal. So, when dividing by 11, the most remainders you might get in a row before one repeats is 10 in a row. But in the case of [latex]\frac{4}{11}[/latex], the remainders repeat after the 4 and 7. This means you keep dividing into 40 or 70 (since you bring the zero down), and that's why in the quotient the digits start repeating.
Now in the case of dividing 2 by 7, the remainders you get as you go along are 6, then 4, then 5, then 1, then 3, and then 2. When you bring down the 0, you are dividing 7 into 20 again, and hence the remainders repeat. Notice that the sequence of remainders (6, 4, 5, 1, 3, and 2) is different than the sequence of digits that repeat in the quotient. The digits that repeat in the quotient are 285714, so [latex]\frac{2}{7}[/latex] = 0.285714285714... or [latex]0. \overline{285714}[/latex].
Since there are only six possible remainders other than zero when dividing by 7, only a sequence of 6 digits could possibly repeat. In this case, all six possible remainders of 7 appeared in the long division.
Key Takeaway - The Number of Digits that Can Repeat
Generally, if [latex]\frac{a}{b}[/latex] is any rational number in the simplest form where b ≠0 and b > a, then there are at most b - 1 possible remainders. So for example, dividing by 9 will have at most 9 - 1 or 8 possible remainders. Now, because there are only b - 1 possible remainders, then only a sequence of b - 1 digits can possibly repeat.
Note: If 0 is a remainder, then the decimal will terminate. So for 9, the possible digits that could be remainders would be 1, 2, 3, 4, 5, 6, 7, and 8, and only a sequence of 8 digits could possibly repeat.
Keep in mind that if you are finding a decimal equivalent for a fraction with 17 in the denominator that there may be up to sixteen remainders in a row before you see any repetition. Now, obviously, there are only 10 digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) in base ten. Note that the sequence of digits repeating in the quotient is totally different than the possible remainders you might get when you divide by 17, since a remainder may be more than a single-digit number.
Exercise 6
a.
b. Do long division to write [latex]\frac{31}{33}[/latex] as a repeating decimal using ellipses and then using the bar over the repeating digits.
Solution
The answer can be written as 0.939393... or as [latex]0. \overline{93}[/latex].
c.
d.
Exercise 7
Use your calculator to write each as a repeating decimal. Write the answer two ways, first with a bar over the repeating digits, and then in long form, using ellipses. Note that your calculator may or may not round the last digit shown. It can't show digits repeating forever, so you have to be savvy enough to know whether the decimal showing on the display is terminal or if it is an approximation.
a. [latex]\frac{5}{9}[/latex]
Solution
[latex]0. \overline{5}[/latex] or as 0.5555...
b. [latex]\frac{5}{7}[/latex]
Solution
[latex]0. \overline{714285}[/latex] or as 0.714285714...
c. [latex]\frac{1}{6}[/latex]
Solution
[latex]0.1 \overline{6}[/latex] or as 0.16666...
d. [latex]\frac{2}{3}[/latex]
Solution
[latex]0. \overline{6}[/latex] or as 0.6666...
e. [latex]\frac{7}{11}[/latex]
Solution
[latex]0. \overline{63}[/latex] or as 0.636363...
f. [latex]\frac{5}{12}[/latex]
Solution
[latex]0.41 \overline{6}[/latex] or as 0.416666...
g. [latex]\frac{8}{15}[/latex]
Solution
[latex]0.5 \overline{3}[/latex] or as 0.53333...
h. [latex]\frac{16}{45}[/latex]
Solution
[latex]0.3 \overline{5}[/latex] or as 0.35555...
i. [latex]\frac{5}{66}[/latex]
Solution
[latex]0.0 \overline{75}[/latex] or as 0.0757575...
Zeros, which are behind a decimal's last non-zero digit, can be added or removed without changing the value of the decimal. If you look at some equivalent fraction, you'll see why this should be true. For example,
[latex]\frac{14}{10} = \frac{140}{1000} = \frac{1400}{10000} = \frac{14000}{100000}[/latex]
These are all equivalent to [latex]\frac{14}{100}[/latex] because the numerator and denominator were multiplied by some power of 10 (10, 100, or 1000) to get one of the other equivalent fractions. If we replace each of the four fractions above with their decimal equivalents, we get 0.14 = 0.140 = 0.1400 = 0.14000. Let's call any zeroes at the end of a decimal's last non-zero digit "trailing zeroes". Then, we could conclude that any number starting with .14 that has trailing zeroes is also equivalent, like 0.1400000.
Two decimals are equal only if one can be made to look identical to the other by adding or removing trailing zeroes. You can also determine if they are equivalent by removing any excess trailing zeroes from each to see if they are identical.
Example 4
For the first decimal given, decide if any of the next five decimals are equal to it.
2.041Â [latex]\longrightarrow[/latex]Â 2.0401Â Â Â Â Â Â 2.0410Â Â Â Â Â 2.04100Â Â Â Â Â 2.00401Â Â Â Â Â 2.4100
Solution:
In order to see if any of the other decimals are equal to 2.041, the first thing we need to do is to make them the same length after the decimal. Since the longest decimal length is five places, all of our decimals, including the given one, should have trailing zeroes added when necessary.
Now we'll have:
2.04100Â [latex]\longrightarrow[/latex]Â 2.04010Â Â Â Â Â Â 2.04100Â Â Â Â Â 2.04100Â Â Â Â Â 2.00401Â Â Â Â Â 2.41000
We can easily see here that the second and third decimal (2.04100) looks like the original one so they are the only decimals that equal.
Exercise 8
To compare two or more decimals that are not equal, but have the same number of digits after the decimal point, you can write each as a fraction with the same denominator and then compare the numerators. For instance, 0.14 is less than 0.21 since fourteen hundredths is less than twenty-one hundredths. Basically, in this case, it's just like comparing whole numbers. You'll be able to determine which is larger by comparing each number as if there were no decimal point. But keep in mind, this only makes sense if the numbers you are looking at have the same number of digits after the decimal point.
Exercise 9
Compare each of the following decimals using <, =, or >.
a. 3.5 and 3.9
Solution
Both decimals have the same number of digits after the decimal point, so we can compare them easily. Since [latex]\frac{5}{10}[/latex] is smaller than [latex]\frac{9}{10}[/latex], then [latex]3.5 < 3.9[/latex].
b. 42.06 and 42.0600
Solution
In this problem, the decimals do not have the same number of digits after the decimal, so we need to add trailing zeroes.
Now we have 42.0600 and 42.0600. Since these are the same, then [latex]42.06 = 42.0600[/latex].
c. 0.098 and 0.089
Solution
Both decimals have three digits behind the decimal point, so we can compare them by looking at the fraction representation. Here [latex]\frac{98}{1000}[/latex] is larger than [latex]\frac{89}{1000}[/latex] so [latex]0.098 > 0.089[/latex].
To compare two or more decimals that are not equal and do not all have the same number of digits after the decimal point, first write each decimal with the same number of digits after the decimal point (by adding trailing zeroes to one or more if necessary). By doing that, you are comparing tenths with tenths, or hundredths with hundredths, etc., as you did in exercise 5.
Exercise 10
Compare each of the following decimals using <, =, or >.
a. 3.51 and 3.488
Solution
Since the decimals do not have the same number of digits after the decimal point, add trailing zeroes to make them the same length:Â 3.510 and 3.488
Now we can compare [latex]\frac{510}{1000}[/latex] and [latex]\frac{488}{1000}[/latex]. 510 is larger than 488, which means that [latex]3.51 > 3.488[/latex]
b. 35.061 and 35.35
Solution
Again, we need to add trailing zeroes to make the decimals have the same number of decimal places:Â 35.061 and 35.350
By comparing [latex]\frac{61}{1000}[/latex] and [latex]\frac{350}{1000}[/latex], we see that 350 is larger than 61, which means that [latex]35.061 < 35.35[/latex]
Rounding Decimals
Definition - Rounding
Rounding or rounding off a decimal means to find a nearby number that has fewer decimal places but still keeps the value of the number intact. First, identify the place value you wish to round to, and then use the digit to the right to determine how to round. If the digit on the right is 5 or greater, then round up, but if the value of the digit on the right is 4 or less, then round down.
Example 5
Use the number 2486.5937 to round to the following place values:
a. the nearest hundredth
b. the nearest tenth
c. the nearest hundred
d. the nearest thousandth
e. the nearest thousand
Solution:
a. The digit in the hundredths place is 9. To determine how to round this 9, we need to look at the digit to the right (3) to make our decision. Since 3 is less than 4, we round down or write the answer as 2486.59.  Rounding down eliminates the last two place values.
b. The digit in the tenths place is 5. Now we'll look at the digit to the right (9) to determine how to round. Since 9 is greater than 5 we round up and write the answer as 2486.6.
c. The digit in the hundreds place is 4 (make sure to read carefully and distinguish between the hundreds place and the hundredths place). The digit to the right is 8, so again we need to round up. The answer is 2500.
d. The digit in the thousandths place is 3. The digit to the right of 3 is 7, which is greater than 5 and will make us round up to get the answer 2486.594.
e. The digit in the thousands place is 2. (Again, be careful to read and distinguish the thousandths place from the thousands place.) The digit to the right is 4, which is not high enough to round up. The answer is written as 2000.
Exercise 11
Use the number 6782.9135 to round the following place values.
Addition and Subtraction of Decimals
When we first started to add whole numbers, we learned that we needed to add place values together. The ones place with the ones place, the tens place with the tens place, and so on. When it comes to adding (and subtracting) decimals, this is still the rule. Unlike adding whole numbers, though, decimals do not always have the same place value for the rightmost digit. For example, we might want to add 6.83 and 13.9. We can see that they both have 3 digits, but the place values don't match. Here, 6.83 ends in the hundredths place while 13.9 ends in the tenths.
A common mistake made is to line up the numbers based on the last place value digit. In our case, that would be the 3 and the 9. As we can see below, not only do the numbers not line up after that, but neither do the decimal points. This causes us not to know where to place the decimal in the final answer. The correct way to add these would have been instead to line up the decimal points, which makes the place values line up as well. When the numbers line up, we can easily add and put the decimal in the correct location.
Let's look at another way to prove why the decimal points must be lined up. We can convert these decimals into fractions and add them that way. So 6.83 will become [latex]6 \frac{83}{100}[/latex] or [latex]\frac{683}{100}[/latex] and 13.9 will become [latex]13 \frac{9}{10}[/latex] or [latex]\frac{139}{10}[/latex]. Now let's try to add them:
[latex]\frac{683}{100} + \frac{139}{10}[/latex] is impossible as long as the denominators are different. We need to use equivalent fractions in order to be able to add correctly.
[latex]\frac{683}{100} + \frac{139}{10} = Â \frac{683}{100} + \frac{1390}{100}Â = \frac{2073}{100}[/latex] or 20.73
Teaching Tip - Addition/Subtraction of Decimals
It is often useful to have the students add trailing zeroes to the problem when adding and subtracting, to be able to see that the decimals have the same number of digits after the decimal point. These zeroes can reinforce the use of zeroes when making equivalent fractions. It can also help them see where the last "digits" line up.
Exercise 12
Subtraction of decimals sets up the same way that addition does - you must line up the decimals. Not only can we not subtract different place values (a hundredth and a tenth), but by not lining up the decimal point, we could potentially get a sign on the answer (a positive versus a negative). Look at the example below:
On the left side, we lined up the last digit, which again has us trying to subtract different place values and has us not knowing where to put the decimal point in the answer. In this problem, we also ended up with a negative answer since "139" is less than "683". Looking at the problem on the right, we can see that when the decimals are properly aligned, the place values will subtract correctly, the decimal point will be in the correct location, and we will be able to have the correct sign on the answer.
Exercise 13
Multiplication and Division
The rule you may remember for multiplying fractions is to multiply the numbers together as if there were no decimal point, and then move the decimal point in from the right the total number of places it is in for both numbers. For instance, [latex]8 \times 0.4[/latex] is done by multiplying 8 times 4 and then moving the decimal point in one place to get 3.2. Similarly, [latex]0.06 \times 0.7[/latex] is done by multiplying 6 times 7 and moving the decimal point in three places (two for 0.06 and one more for 0.7 for a total of three) to get 0.042. Many people make this harder than it really is and don't realize they can easily multiply 0.3 and 0.4 in their heads. It's as simple as [latex]0.3 \times 0.4[/latex] and moving the decimal in two places to get 0.12. Now, how about [latex]1.1 \times 1.2[/latex]? It's simply 11 times 12 with the decimal moved in two places: 1.32.
Definition - Multiplication of Decimals
If there are n digits to the right of the decimal in one number and m digits to the right of the decimal in another number, then multiply the numbers as if they were whole numbers. Place the decimal point in the answer so there are n + m digits to the right of the decimal point.
Let's observe why this rule for multiplying decimals works by rewriting the numbers as fractions first. The key here is to write numbers greater than or equal to one as improper fractions. Then multiply (without canceling or reducing) the fractions. Lastly, rewrite the fraction as a decimal.
Example 6
Solve [latex]8 \times 0.4[/latex] using fractions.
Solution:
First we need to convert the decimals into equivalent fractions and then use the rules for multiplication of fractions to find the answer.
[latex]8 \times 0.4[/latex] = [latex]\frac{8}{1} \times \frac{4}{10} = \frac{32}{10}[/latex] = 3.2
(Notice the decimal point is one place in for 0.4.)
Example 7
Solve [latex]1.2 \times 1.01[/latex] using fractions.
Solution:
Again, we will need to convert the decimals into equivalent fractions before multiplying them to get the answer.
[latex]1.2 \times 1.01[/latex] = [latex]\frac{12}{10} \times \frac{101}{100} = \frac{1212}{1000}[/latex] = 1.212
(Notice the decimal point is three places in, one for 1.2 plus two more for 1.01.)
Exercise 14
Multiply the following decimals mentally, and then do it again by showing the same steps as shown in the previous two examples, where each decimal is first written as a fraction, then multiply the numerators and denominators, and then convert that answer (don't simplify) to a decimal. Do not use your calculator.
a. [latex]0.4 \times 0.07[/latex]
Solution
[latex]0.4 \times 0.07 = 0.028[/latex]
[latex]0.4 \times 0.07[/latex] = [latex]\frac{4}{10} \times \frac{7}{100} = \frac{28}{1000} = 0.028[/latex]
b. [latex]1.6 \times 0.2[/latex]
Solution
[latex]1.6 \times 0.2 = 0.32[/latex]
[latex]1.6 \times 0.2[/latex] = [latex]\frac{16}{10} \times \frac{2}{10} = \frac{32}{100} = 0.32[/latex]
c. [latex]0.25 \times 0.3[/latex]
Solution
[latex]0.25 \times 0.3 = 0.075[/latex]
[latex]0.25 \times 0.3[/latex] = [latex]\frac{25}{100} \times \frac{3}{10} = \frac{75}{1000} = 0.075[/latex]
d. [latex]2.2 \times 0.3[/latex]
Solution
[latex]2.2 \times 0.3 = 0.66[/latex]
[latex]2.2 \times 0.3[/latex] = [latex]\frac{22}{10} \times \frac{3}{10} = \frac{66}{100} = 0.66[/latex]
We can use a similar approach to dividing decimals that we used with multiplying decimals. This time, though, we'll figure out where the decimal needs to go first, then we'll divide the numbers as if they were whole numbers.
Let's see how basic division with a whole number and a decimal works first by solving [latex]7.02 \div 3[/latex]
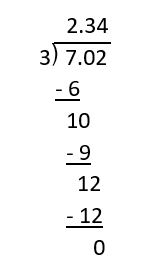
When we look at what's happening, we can see that the place value (hundredths) on 702 never changed. We were able to invert the second fraction and turn the division problem into a multiplication problem. However, when we switched the denominators, we found out that we were really just dividing the whole numbers 702 and 3. The place value was still the hundredths, and our final answer 2.34 reflects this.
Now, let's try the problem again, but this time we'll divide 7.02 by 0.3 and see if the decimal point on our divisor makes any difference.
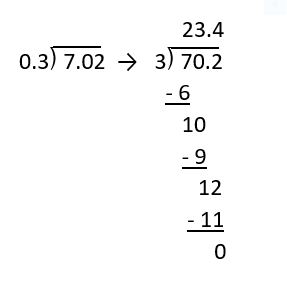
When solving a problem where the divisor is a decimal, the correct thing to do is to move the decimal on the divisor to the end of that number, making it a whole number. We then need to repeat the same move on the dividend, so 1 decimal move on the divisor means to move 1 place on the dividend. This gives us [latex]7.02 \div 0.3 = 70.2 \div 3[/latex].
Now, let's use the fractions again to show why this move is needed and critical in finding the correct answer.
[latex]7.02 \div 0.3 = \frac{702}{100} \div \frac{3}{10} = \frac{702}{100} \times \frac{10}{3} = \frac{702}{3} \times \frac{10}{100} = 234 \times \frac{1}{10} = \frac{234}{10} = 23.4[/latex]
The problem starts off the same way when we convert the decimals into fractions, but once we switch the denominators, we see something new happen. This time our hundredths place is going to change when we reduce [latex]\frac{10}{100}[/latex] down to [latex]\frac{1}{10}[/latex]. We simplified or "lost" a zero, which caused us to change our ending place value. This change is the reason that we move the decimal on the divisor in the beginning. By doing it first, we eliminate the issue of where to put the decimal in the quotient. It also makes it easier to divide when the divisor is a whole number.
There is one other thing that we need to address with division - division with decimals can be unpredictable. We might have an idea about what place value the answer will have, but this isn't always set in stone. We could have a completely different and unexpected outcome.
Examples 8
Divide the following two examples completely with no remainders.
a. [latex]7.02 \div 4[/latex]
Solution:
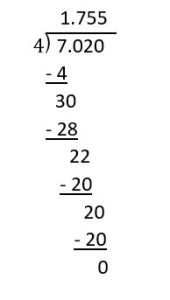
When we started the problem, 7.02 was a decimal in the hundredths place, and we needed to divide it by a whole number. Unlike the problem we worked on above, we didn't end up with a quotient in the hundredths; we got one in the thousandths. Since 4 doesn't divide 702 evenly (there is a remainder), then 4 won't divide 7.02 and have the same place value in the answer. When a problem like this comes up, we need to add trailing zeroes to our dividend and keep dividing until we determine if we have a repeating or terminating decimal for an answer.
b. [latex]9 \div 0.75[/latex]
Solution:
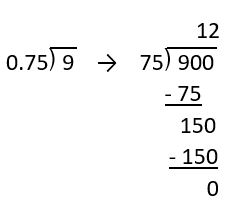
This time we needed to move the decimal place on the divisor two times and on the dividend two times, giving us [latex]900 \div 75[/latex]. Since both numbers are whole numbers and 75 divides into 900 evenly, the quotient was also a whole number.
Exercises 15
Divide the following problems completely with no remainders.
a. [latex]0.36 \div 6[/latex]
Solution
b. [latex]0.9 \div 0.45[/latex]
Solution
c. [latex]0.125 \div 0.05[/latex]
Solution
>
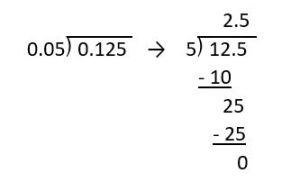
d. [latex]1.84 \div 0.04[/latex]
Solution
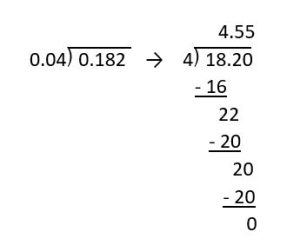
e. [latex]0.0828 \div 6[/latex]
Solution
 
Percents
Definition - Percent
The word percent is from the Latin phrase per centum, which means "for each hundred" or "by the hundred". This means that when we study percents, we're really just studying fractions with a denominator of 100.
[latex]p\% = \frac{p}{100}[/latex] where p is any non-negative number
Since percents have a denominator of 100, we can find an equivalent decimal approximation. For example [latex]12\% = \frac{12}{100} = 0.12[/latex].
Exercise 16
Convert the following percents into equivalent decimals.
a.Â
b.Â
c.Â
d.Â
e.Â
Now that we understand what a percent is, we can use it to solve problems.
Cross Multiplication with Percents
Problems involving percents usually take on one the these three forms:
- Find the percent of a number.
- Find what percent one number is of another number.
- Finding a number when a percent of that number is known.
In order to set up these types of problems, we can set up the following proportion:
[latex]\frac{part}{whole} = \frac{percent}{100}[/latex]
We've used cross multiplication before, so we can use it again in the same way to solve these percent problems.
Example 9
Sean answered 8 questions on a math test last week. These correct answers gave him a score of 40%. How many questions were on his test?
Solution:
He answered 8 questions correctly, so this number is "part" of the test. We're looking for the total number of questions on the test, so we're looking for the "whole". We can use "x" as the missing whole when we set up the proportion.
[latex]\frac{8}{x} = \frac{40}{100}[/latex]
By using cross multiplication, we can get :
[latex]8 \times 100 = x \times 40[/latex]
[latex]800 = 40x[/latex]
[latex]\frac{800}{40} = \frac{40x}{40}[/latex]
[latex]20 = x[/latex]
This means that there were 20 questions on the whole test.
The example above wanted us to find the "whole" or a number when we were given the percent of that number. In the next example, let's look for a different value.
Example 10
Marcus has 75 marbles in his collection. If blue marbles make up 40% of his collection, then how many blue marbles does he have?
Solution:
This time we know the total number or "whole" and are looking for a "part" of the whole. This proportion looks like this:
[latex]\frac{x}{75} = \frac{40}{100}[/latex]
We can cross multiply again to find the blue marbles.
[latex]x \times 100 = 75 \times 40[/latex]
[latex]100x = 3000[/latex]
[latex]\frac{100x}{100} = \frac{3000}{100}[/latex]
[latex]x = 30[/latex]
This means that there were 30 blue marbles in the collection.
Exercise 17
A basketball player practiced his shooting over the weekend. If he made 270 baskets, and this was 45% of the total he shot, how many total attempts did he have?
Solution
Since 270 was only 45% of the total, this is the "part" and we are looking for the "whole".
[latex]\frac{270}{x} = \frac{45}{100}[/latex]
[latex]270 \times 100 = x \times 45[/latex]
[latex]27000 = 45x[/latex]
[latex]\frac{27000}{45} = \frac{45x}{45}[/latex]
[latex]600 = x[/latex]
This means that he attempted 600 shots.
Exercise 18
A teacher gave a project that was worth 205 points. Since the scores were low, the teacher decided to give a bonus worth 7% of the total possible points. How many bonus points did the teacher give each student?
Solution
This time, we know the total number or "whole" was 205 points, and we are looking for a "part" of the whole.
[latex]\frac{x}{205} = \frac{7}{100}[/latex]
[latex]x \times 100 = 205 \times 7[/latex]
[latex]100x = 1435[/latex]
[latex]\frac{100x}{100} = \frac{1435}{100}[/latex]
[latex]x = 14.35[/latex]
The teacher gave 14.35 bonus points to each student.
Exercise 19
Jessica took a math test with 75 possible points. If she got 51 points correct, what was her percentage of incorrect points?
Solution
The 51 points that she got correct are the "part", and the total 75 points is the "whole".
[latex]\frac{51}{75} = \frac{x}{100}[/latex]
[latex]51 \times 100 = 75 \times x[/latex]
[latex]5100 = 75x[/latex]
[latex]\frac{5100}{75} = \frac{75x}{75}[/latex]
[latex]68 = x[/latex]
Jessica got 68% correct on the test, so this means that she got 100% - 68% or 32% incorrect.
Often, we are asked to find the amount of change that a value has based on a simple quantity. For example, if we know that John ran 3 miles today and 5 miles next week, then we can subtract 5 and 3 and find out that he increased is run by 2 miles. Likewise, suppose Mia ran 4 miles today and only 2 miles next week. We can again subtract 4 and 2 and find out that Mia decreased her run by 2 miles. This type of increase or decrease can be found by subtracting the two amounts, but when percents are involved, the calculation requires more work.
An easy way to find the percent increase or decrease of an amount is to use a variation of the distributive property.
Percent Increase/Decrease
Percent Increase from A to B:Â [latex]B = A + p\% \times A[/latex]
Percent Decrease from A to B:Â [latex]B = A - p\% \times A[/latex]
In both cases, you are starting with an initial amount and then either adding to increase or subtracting to decrease and certain percentage of that amount. Let's look at a few examples to see how the formulas work.
Example 11
If a reading tablet costs $187 and if the price of the tablet goes up by 6%, then what will the new price of the tablet be?
Solution:
The original price of the tablet is $187 so this is the "A" value. We are looking for the new price or the increased price "B".
[latex]B = 187 + 6\% \times 187[/latex]
[latex]B = 187 + 0.06 \times 187[/latex]
[latex]B = 187 + 11.22[/latex]
[latex]B = \$198.22[/latex]
The price of a condo on the Gulf Coast for a week in the spring increased by 15%. The new price is $2300. What was the price before the increase?
Solution:
This time, we know the increased price of $2300, but the original price is unknown, so we need to find the "A" value.
[latex]2300 = A + 15\% \times A[/latex]
[latex]2300 = A + 0.15 \times A[/latex]
[latex]2300 = A + 0.15A[/latex]
[latex]2300 = 1.15A[/latex]
[latex]\frac{2300}{1.15} = \frac{1.15A}{1.15}[/latex]
[latex]\$2000 = A[/latex]
Example 12
If a reading tablet costs $187 and if the price of the tablet goes down by 6% during a sale, what will the new price of the tablet be?
Solution:
The original price of the tablet is $187, so this is the "A" value. We are looking for the new price or the decreased price "B".
[latex]B = 187 - 6\% \times 187[/latex]
[latex]B = 187 - 0.06 \times 187[/latex]
[latex]B = 187 - 11.22[/latex]
[latex]B = \$175.78[/latex]
The price of a condo on the Gulf Coast for a week in the fall decreased by 15%. The new price is $2300. What was the price before the decrease?
Solution:
This time, we know the decreased price of $2300, but the original price is unknown, so we need to find the "A" value.
[latex]2300 = A - 15\% \times A[/latex]
[latex]2300 = A - 0.15 \times A[/latex]
[latex]2300 = A - 0.15A[/latex]
[latex]2300 = 0.85A[/latex]
[latex]\frac{2300}{0.85} = \frac{0.85A}{0.85}[/latex]
[latex]\$2705.88 = A[/latex]
Exercise 20
A room at a 4-star hotel originally cost $230 per night. If the price was increased by 30% during a busy period, what is the new cost of the room?
Solution
[latex]B = 230 + 30\% \times 230[/latex]
[latex]B = 230 + 0.06 \times 230[/latex]
[latex]B = 230 + 138[/latex]
[latex]B = \$368[/latex]
Exercise 21
A local store is putting a laptop computer on sale for $700 as part of its Black Friday sales. If the price decreases by 20% during the sale, then what was the original price?
Solution
[latex]700 = A - 20\% \times A[/latex]
[latex]700 = A - 0.20 \times A[/latex]
[latex]700 = A - 0.20A[/latex]
[latex]700 = 0.80A[/latex]
[latex]\frac{700}{0.80} = \frac{0.80A}{0.80}[/latex]
[latex]\$875 = A[/latex]