38 Homework
- Submit homework separately from this workbook and staple all pages together. (One staple for the entire submission of all the unit homework)
- Start a new module on the front side of a new page and write the module number on the top center of the page.
- Answers without supporting work will receive no credit.
- Some solutions are given in the solutions manual.
- You may work with classmates but do your own work.
Do each of the following steps using your C-strips.
- State how many C-strips (each an equal part of the whole) make up one unit.
- State which C-strip makes up one part of the whole.
- State the fraction that the C-strip in part b represents.
- State how many of the C-strips in part b you need to make into a train.
- State which C-strip is the length of the train you made in part c
a. If S represents 1 unit, then which C-strip represents [latex]\frac{7}{11}[/latex]?
b. If H represents 1 unit, then which C-strip represents [latex]\frac{2}{3}[/latex]?
c. If P represents 1 unit, then which C-strip represents [latex]\frac{3}{2}[/latex]?
d. If L represents 1 unit, then which C-strip represents 3 ?
e. If Y represents 1 unit, then which C-strip represents [latex]\frac{6}{5}[/latex]?
f. If O represents 1 unit, then which C-strip represents [latex]\frac{1}{2}[/latex]?
g. If B represents 1 unit, then which C-strip represents [latex]\frac{4}{3}[/latex]?
Do each step using your C-strips.
- State how many C-strips will make up the named C-strip stated in the problem.
- Which C-strip makes up one equal part?
- State the fraction that the C-strip in part b represents.
- State how many of the C-strips in part b will make up one unit.
- Form the unit by making a train from the equal parts (C-strip in part b) and state which C-strip has the same length as that train.
a. If O represents [latex]\frac{5}{6}[/latex], then which C-strip is 1 unit?
b. If W represents [latex]\frac{1}{7}[/latex], then which C-strip is 1 unit?
c. If D represents [latex]\frac{3}{2}[/latex], then which C-strip is 1 unit?
d. If N represents [latex]\frac{4}{3}[/latex], then which C-strip is 1 unit?
e. If D represents 3, then which C-strip is 1 unit?
f. If K represents [latex]\frac{7}{9}[/latex], then which C-strip is 1 unit?
Do each step using your C-strips.
- State which C-strip is one unit.
- State which C-strip is the answer.
a. If N represents [latex]\frac{2}{3}[/latex], then which C-strip represents [latex]\frac{1}{4}[/latex]?
b. If D represents [latex]\frac{3}{4}[/latex], then which C-strip represents [latex]\frac{3}{2}[/latex]?
c. If B represents [latex]\frac{3}{2}[/latex], this which C-strip represents [latex]\frac{4}{3}[/latex]?
Use your fraction arrays to determine all fractions on the fraction array that are equivalent to 3/4. Do this by finding 3/4 on the array, and seeing what other numbers are the same length. Include a diagram.
Use your multiple strips to write 6 fractions equivalent to 5/6. Draw the strips.
Use your multiple strips to write 6 fractions equivalent to 3/8 Draw the strips.
Compare 3/8 and 1/3 using models. Show all of the steps, and explain the procedure as shown in this module.
Add 3/8 and 1/3 using models. Show all of the steps, and explain the procedure as shown in this module.
Do the following subtraction using models: 3/5 – 1/4. Show all of the steps, and explain the procedure as shown in this module.
Do the following multiplications using models. Show all of the steps, and explain the procedure as shown in this module.
a. 3/8 [latex]\cdot[/latex] 2/5
b. 4/7 [latex]\cdot[/latex] 2/3
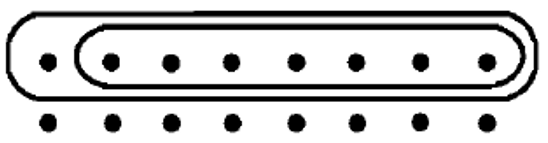
By looking at the final drawing someone made to model a multiplication of two fractions, determine which multiplication was performed, and then state the answer.
a. 5/6 [latex]\cdot[/latex] 2/3 OR 2/3 [latex]\cdot[/latex] 5/6
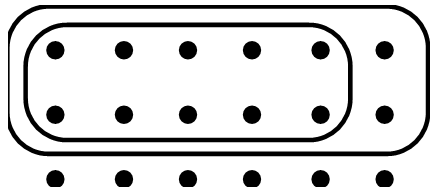
b. 1/2 [latex]\cdot[/latex] 7/8 OR 7/8 [latex]\cdot[/latex] 1/2
If all of the dots shown for each problem represent 1 unit, determine the multiplication problem that someone did to get the answer, and state the answer.
a.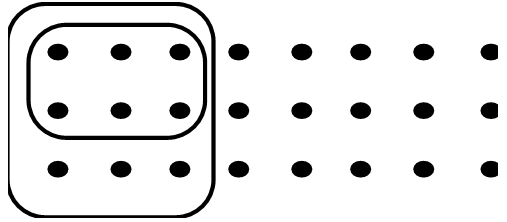 
b.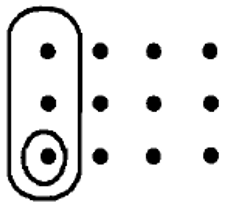 
Fill in the chart showing how to do the following multiplications using C-strips. The multiplication is in the first column. State an appropriate choice for the unit (name a C-strip, or sum of two C-strips) in the second column. Write the C-strip obtained after the first part of the multiplication (which is the second fraction as a part of the unit) in the third column. Then, do the final multiplication, and write the C-strip obtained in the fourth column. In the fifth column, write a fraction using C-strips putting the final unit obtained in the fourth column as the numerator, and the unit in the denominator. Then, in the last column, write the answer as a fraction. Do not simplify.
| a. | [latex]\frac{1}{3} \cdot \frac{2}{3}[/latex] | |||||
| b. | [latex]\frac{1}{2} \cdot \frac{5}{6}[/latex] |
Perform the following division using the box and dot methods. First define the unit. Then explain and show all of the steps. Include diagrams.
a. 5 [latex]\div[/latex] 1/3
b. 3/4 [latex]\div[/latex] 1/3
Determine if the following statements are true or false by comparing cross products.
a. 19/23 = 57/69
b. 24/37 = 68/91
Write each fraction in simplest form using each of the two methods:
(1) prime factorization and
(2) finding GCF.
a. [latex]\frac{216}{420}[/latex]
b. [latex]\frac{195}{286}[/latex]
Use cross products to compare each of the following fractions. Use < or >.
a. 18/23 and 5/8
b. 11/18 and 121/250
Find 3 rational numbers, written with a common denominator, between 3/8 and 5/8.
Find 3 rational numbers, written with a common denominator, between 1/2 and 4/7.
a. 21 of John’s students have cats at home. This represents 7/10 of John’s students. How many students are in John’s class? Solve the problem using models. Explain how the model works.
b. At an elementary school, 38 teachers drive alone to work. This represents 2/3 of the teachers. How many teachers work at the school? Solve the problem using models. Explain how the model works.
Write in words how to read each of the following decimals.
a. 0.7
b. 0.67
c. 3.28
d. 19.835
Multiply the following decimals mentally then do it again by showing the same steps as shown in this module..
a. (0.3)(0.8)
b. (1.2)(0.4)
c. (1.22)(2.3)
d. (3.2)(2.41)
For each fraction, determine if it can be written as an equivalent fraction with a power of ten in the denominator. If a fraction cannot be written as a terminal decimal, explain why not. Otherwise, show ALL of the steps to write it as a terminal decimal.
a. [latex]\frac{11}{16}[/latex]
b. [latex]\frac{3}{125}[/latex]
c. [latex]\frac{1}{12}[/latex]
d. [latex]\frac{9}{40}[/latex]
e. [latex]\frac{21}{56}[/latex]
Rewrite each of the following decimals as simplified fractions. For repeating decimals, use the techniques shown in this module. Then, check your answer using a calculator by dividing the numerator by the denominator to see if the result matches the original problem.
a. [latex]0.\bar{7}[/latex]
b. [latex]0.\overline{72}[/latex]
c. [latex]0.\overline{235}[/latex]
d. [latex]0.2\bar{5}[/latex]
e. [latex]0.3\overline{42}[/latex]