42 Module 9.2 Addition and Subtraction of Fractions
Louisiana Student Standards
Standard Number |
Description of Standard |
| 4.NF.B.3c. | Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction. |
| 4.NF.B.3d. |
Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem. |
| 5.NF.A.1 | Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators. |
| 5.NF.A.2a. |
Solve word problems involving addition and subtraction of fractions referring to the same whole, including cases of unlike denominators, e.g., by using visual fraction models or equations to represent the problem. |
You will need: Centimeter Strips (Material Cards 16A-16L), Fraction Tiles (Material Card 25)
Exploration Activity
Set-Up: Take out your fraction tiles and line up [latex]\frac{5}{12}[/latex] and [latex]\frac{1}{3}[/latex] in one long line. Put them directly next to each other so you have one single strip of length [latex]\frac{5}{12}+\frac{1}{3}[/latex].
- Underneath your setup, lay out the full row of fourths. (All four pieces of size [latex]\frac{1}{4}[/latex].) Line them up so your first [latex]\frac{1}{4}[/latex] piece starts at the same place as your first [latex]\frac{1}{12}[/latex] piece.How many [latex]\frac{1}{4}[/latex] pieces does it take to exactly match [latex]\frac{5}{12}+\frac{1}{3}[/latex]?
- Remove the fourth pieces. Now underneath your set-up, lay out the full eighths strip. Again, line it up so your first [latex]\frac{1}{8}[/latex] piece starts at the same place as your first [latex]\frac{1}{12}[/latex] piece.How many [latex]\frac{1}{8}[/latex] pieces does it take to exactly match [latex]\frac{5}{12}+\frac{1}{3}[/latex]?
- Consider your answers to parts (a) and (b). How do the two fractions compare? Explain why this makes sense.
Solution
The fractions are [latex]\frac{3}{4}[/latex] and [latex]\frac{6}{8}[/latex]. These are equivalent fractions, so they have the exact same value.
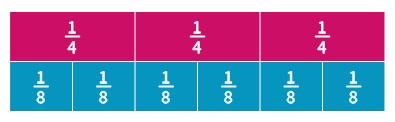
This makes sense because they both lined up with the same thing, so they must be the same length.

- Remove the eighth piece. Now, line up a single [latex]\frac{1}{3}[/latex] piece with twelfths underneath. How many [latex]\frac{1}{12}[/latex] pieces does it take to equal a single [latex]\frac{1}{3}[/latex] piece?
- Based on your answer to (d), what would you expect [latex]\frac{5}{12}+\frac{1}{3}[/latex] to be in terms of twelfth pieces?
- Compare your answer from (e) to your answer from (a). Why does this make sense?
Solution
As with [latex]\frac{6}{8}[/latex], [latex]\frac{9}{12}[/latex] is also equivalent to [latex]\frac{3}{4}[/latex]. Any fraction equivalent to [latex]\frac{3}{4}[/latex] will perfectly line up with [latex]\frac{5}{12}+\frac{1}{3}[/latex].
Addition of Fractions with the Same Denominator
As we do with other types of numbers, we can add or subtract fractions. When two fractions have a common denominator, addition and subtraction are straightforward. You are just counting how many of that type of piece you have. Let's add [latex]\frac{3}{10}[/latex] and [latex]\frac{5}{10}[/latex] using fraction tiles.
Example 1
Add [latex]\frac{3}{10}[/latex] and [latex]\frac{5}{10}[/latex] using fraction tiles.
Solution:
When we line up three pieces of size [latex]\frac{1}{10}[/latex] next to five pieces of size [latex]\frac{1}{10}[/latex], we have a total of eight pieces of size [latex]\frac{1}{10}[/latex], so our answer is [latex]\frac{8}{10}[/latex].
![]()
Since [latex]\frac{8}{10}[/latex] is equivalent to [latex]\frac{4}{5}[/latex] we could also have given the answer [latex]\frac{4}{5}[/latex].

Many elementary classrooms have a supply of fraction tiles/bars, but these are limited because they do not have many different denominators. Typically, they only have denominators of [latex]1, 2, 3, 4, 5, 6, 8, 10,[/latex] and [latex]12[/latex].
Another way to visualize the addition of fractions is with our C-strips.
Example 2
Find the sum [latex]\frac{7}{11}+\frac{3}{11}[/latex] using C-strips.
Solution:
Consider two fractions, [latex]\frac{7}{11}[/latex] and [latex]\frac{3}{11}[/latex].
-
- Since our denominator is [latex]11[/latex], let the C-strip [latex]S[/latex] (with a length of [latex]11[/latex]) represent one unit, which C-strips represent [latex]\frac{7}{11}[/latex] and [latex]\frac{3}{11}[/latex] respectively?
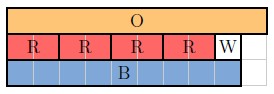
If the C-strip [latex]S[/latex] (with a length of [latex]11[/latex]) represents one unit, then [latex]K[/latex] (with a length of [latex]7[/latex]) represents [latex]\frac{7}{11}[/latex]; and [latex]L[/latex] (with a length of [latex]3[/latex]) represents [latex]\frac{3}{11}[/latex].
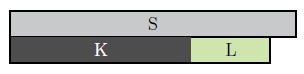
-
- Which C-strip represents the sum [latex]\frac{7}{11}+\frac{3}{11}[/latex]?
The sum of [latex]K[/latex] and [latex]L[/latex] can be represented by [latex]O[/latex] (with a length of [latex]10[/latex])

-
- Write the sum as a fraction where the C-strip [latex]S[/latex] represents one unit.
When the C-strip [latex]S[/latex] represents one unit, the sum [latex]O[/latex] represents [latex]\frac{10}{11}[/latex].
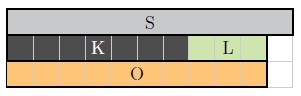
Example 2 shows us that [latex]\frac{7}{11}[/latex] [latex]+[/latex] [latex]\frac{3}{11}[/latex] = [latex]\frac{10}{11}[/latex].
The advantage of fraction tiles is that they are automatically made to have the same unit size. With C-strips, you have to determine which piece will represent a unit, but this makes the C-strips more flexible, meaning you can model a wider variety of problems with C-strips than you can with fraction tiles.
Exercise 1
Find the following sums using the physical manipulative listed.
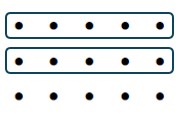
a. [latex]\frac{2}{5}+\frac{1}{5}[/latex] (Fraction tiles)
Solution
![]()
Answer: [latex]\displaystyle\frac{3}{5}[/latex]
b. [latex]\frac{2}{7}+\frac{4}{7}[/latex] (C-strips)
Solution

Answer: [latex]\frac{6}{7}[/latex]
c. [latex]\frac{3}{8}+\frac{5}{8}[/latex] (Fraction tiles or C-strips)
Solution
![]()
Answer: [latex]\frac{8}{8}[/latex] or equivalently, [latex]1[/latex]
The same denominator indicates the same unit, so when we add two fractions with a common denominator, we just keep the denominator and add the numerators to get the new numerator. This is because we are just counting how many pieces of that size we have. In general, we can write the rule as below:
[latex]\frac{a}{b} + \frac{c}{b} = \frac{a+c}{b}[/latex].
Addition of Fractions with Different Denominators
When two fractions have different denominators, we cannot add them directly. Let's consider [latex]\frac{1}{3}[/latex] and [latex]\frac{1}{2}[/latex]. These pieces are different sizes. It is like trying to add 1 teaspoon and 1 tablespoon. We need to convert them to the same type of item before we can add them together. In other words, we need to use equivalent fractions! But, which denominator should we use?
You may already know which denominator to use, but let's suppose you are a student that is unsure. We can use fraction bars to check which denominators will give us equivalent fractions for both [latex]\frac{1}{3}[/latex] and [latex]\frac{1}{2}[/latex].
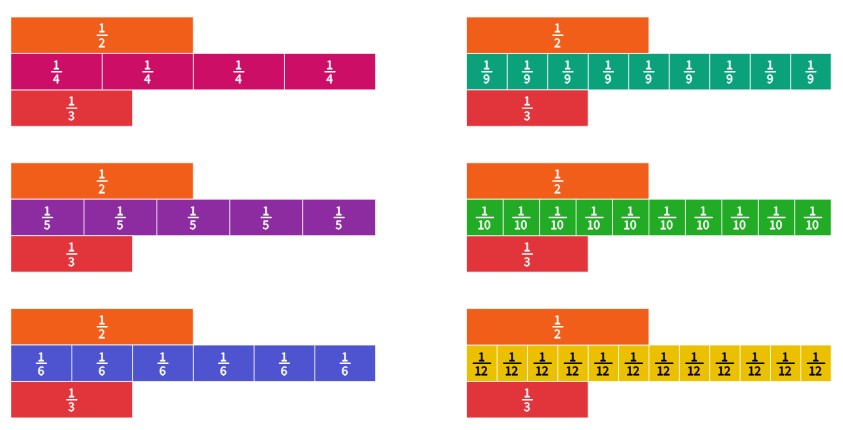
If we line up fourth pieces with our [latex]\frac{1}{3}[/latex] and [latex]\frac{1}{2}[/latex] piece, we see that [latex]\frac{2}{4}[/latex] lines up perfectly with [latex]\frac{1}{2}[/latex], but no amount of fourth pieces will line up with the [latex]\frac{1}{3}[/latex] piece. Continuing through with various denominators, we see that sixth and twelfth pieces will line up with both [latex]\frac{1}{3}[/latex] and [latex]\frac{1}{2}[/latex]. We can use either 6 or 12 as our common denominator, so let us use 6.
According to our fraction bars, [latex]\frac{1}{3}=\frac{2}{6}[/latex] and [latex]\frac{1}{2}=\frac{3}{6}[/latex]. Thus, [latex]\frac{1}{3}+\frac{1}{2}[/latex] is the same as [latex]\frac{2}{6}+\frac{3}{6}[/latex].
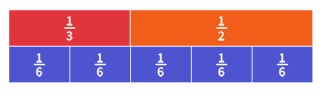
Once we have a common fraction type, we count how many pieces we have.
Answer: [latex]\frac{5}{6}[/latex]
Concept Check: If we had chosen to use twelfths, we would have had [latex]\frac{4}{12}+\frac{6}{12}=\frac{10}{12}[/latex].
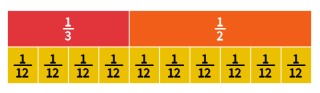
Since [latex]\frac{10}{12}[/latex] and [latex]\frac{5}{6}[/latex] are equivalent fractions these are the same answer. Are these the only two denominators we could have used as a common denominator between [latex]\frac{1}{3}[/latex] and [latex]\frac{1}{2}[/latex]?
Solution
Not at all! They are the only denominators in our fraction tiles that work, but there are a lot more denominators. In fact, any multiple of 2 and 3 will work. We could use 6, 12, 18, 24, 30, 36, 42, etc. Typically, we prefer to use the least common multiple because it keeps the numbers smaller, but it is not required.
Perhaps your school does not have access to fraction tiles/bars. We can also find a common denominator using C-strips. Again, it comes down to multiples.
Reconsider [latex]\frac{1}{3}+\frac{1}{2}[/latex]. Which [latex]C[/latex]-strip should we use to represent one unit? Notice that [latex]\frac{1}{3}[/latex] and [latex]\frac{1}{2}[/latex] have two different units! If we are going to add fractions, they need to come from the same unit.
We need to represent [latex]\frac{1}{3}[/latex] and [latex]\frac{1}{2}[/latex] using the same unit. This requires a unit that is divisible by both [latex]3[/latex] and [latex]2[/latex]. In other words, the unit should be one of the common multiples of [latex]3[/latex] and [latex]2[/latex]. For convenience, we usually choose the least common multiple ([latex]LCM[/latex]) of the two denominators, which is [latex]6[/latex]. Let the C-strip [latex]D[/latex], which has length six represent one unit. Then [latex]\frac{1}{3}[/latex] can be represented by [latex]R[/latex] (length 2) and [latex]\frac{1}{2}[/latex] (length 3) can be represented by [latex]L[/latex].

Therefore, the sum of [latex]\frac{1}{3}[/latex] and [latex]\frac{1}{2}[/latex] would be represented by a C-strip with length [latex]5[/latex], that is, [latex]Y[/latex], which represents [latex]\frac{5}{6}[/latex] when [latex]D[/latex] is a unit.
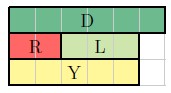
In summary, what we've done with the C-strips can be written as
[latex]\frac{1}{3} + \frac{1}{2} = \frac{2}{6} + \frac{3}{6} = \frac{5}{6}[/latex].
Our fraction tiles and C-strips are limited by the sizes we have. You can combine C-strips to get larger size unit pieces, but there is also another model we can use to visualize this process: the dot model.
Example 3
Use the dot model to add [latex]\frac{2}{5}[/latex] and [latex]\frac{3}{7}[/latex].
Solution:
Step 1: Let [latex]1[/latex] unit be a [latex]5[/latex] by [latex]7[/latex] array of dots, for a total of [latex]35[/latex] dots, as shown below. Since there are [latex]35[/latex] dots to a unit, each dot equals [latex]\frac{1}{35}[/latex] of a unit.

Step 2: Since there are [latex]5[/latex] rows, the unit can be broken up into [latex]5[/latex] equal parts by circling the rows, as shown below:

Therefore, each row is [latex]\frac{1}{5}[/latex] of a unit. Notice there are [latex]7[/latex] dots in [latex]\frac{1}{5}[/latex] of a unit:

Step 3: Similarly, since there are [latex]7[/latex] equal columns, each column is [latex]\frac{1}{7}[/latex] of a unit:


Step 4: Now that we have properly defined the unit fraction, [latex]\frac{1}{5}[/latex], we are ready to show what [latex]\frac{2}{5}[/latex] looks like. Since [latex]\frac{1}{5}[/latex] is [latex]1[/latex] row of dots, then [latex]\frac{2}{5}[/latex] must be [latex]2[/latex] rows of dots. Therefore, [latex]\frac{2}{5}[/latex] is shown below:
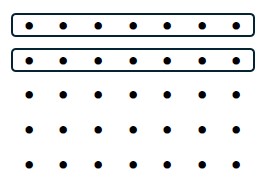
Notice that [latex]\frac{2}{5}[/latex] contains [latex]14[/latex] dots, which is equivalent to [latex]\frac{14}{35}[/latex].
Step 5: Similarly, we can show what [latex]\frac{3}{7}[/latex] looks like. Since [latex]\frac{1}{7}[/latex] is [latex]1[/latex] column of dots, then [latex]\frac{3}{7}[/latex] must be [latex]3[/latex] columns of dots. Therefore, [latex]\frac{3}{7}[/latex] is shown below:
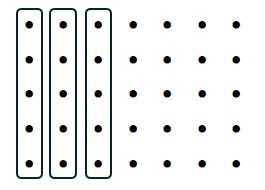
Notice that [latex]\frac{3}{7}[/latex] contains [latex]15[/latex] dots, which is equivalent to [latex]\frac{15}{35}[/latex].
Step 6: Now, we add all of our dots together. We have [latex]14+15=29[/latex] dots total.
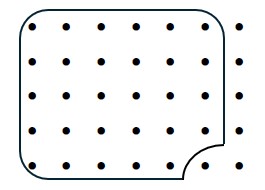
That is, [latex]\frac{2}{5}+\frac{3}{7}=\frac{29}{35}[/latex].
In Example 3, we used the dot model to visualize the following math procedure:
[latex]\frac{2}{5}+\frac{3}{7}=\frac{14}{35}+\frac{15}{35}=\frac{29}{35}[/latex].
Exercise 2
Find the following sums using the physical manipulative listed. Be sure you can explain what is happening at every step in the process.
a. [latex]\frac{1}{2}+\frac{1}{6}[/latex] (Fraction tiles)
Solution

Answer: [latex]\frac{2}{3}[/latex]
Any fraction equivalent to [latex]\frac{2}{3}[/latex] will also work, such as [latex]\frac{4}{6}[/latex] or [latex]\frac{6}{9}[/latex] or [latex]\frac{8}{12}[/latex].
b. [latex]\frac{4}{5}+\frac{1}{10}[/latex] (C-strips)
Solution
Answer: [latex]\frac{9}{10}[/latex]
d. [latex]\frac{2}{3}+\frac{2}{5}[/latex] (Dot Model)
Solution
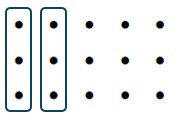
[latex]16[/latex] dots of size [latex]\frac{1}{15}[/latex]
Answer: [latex]\frac{16}{15}[/latex]
c. [latex]\frac{3}{4}+\frac{1}{3}[/latex] (Fraction tiles)
Solution

Answer: [latex]1\;\frac{1}{12}[/latex]
Teaching Tip: One of the most common misconceptions about fractions is people believing all fractions are between zero and one. Whenever possible, throw in a fraction that is larger than one or below zero to help your students from falling into this trap!
Subtraction of fractions is similar to addition in that it all comes down to needing a common unit.
Subtraction of Fractions with the Same Denominator
When dealing with fractions that have the same denominator, you can either use the missing-addend visualization or take-away visualization of subtraction.
Example 4
Find the difference [latex]\frac{7}{10}-\frac{3}{10}[/latex] using fraction tiles.
Solution:
Missing-Addend Approach
Lay out the minuend (first number) and lay the subtrahend (second number) underneath it.
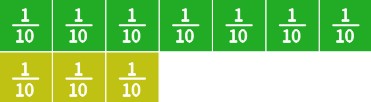
We want to know what can be added to [latex]\frac{3}{10}[/latex] to equal [latex]\frac{7}{10}[/latex] . Filling in the gap allows us to see that four pieces of size [latex]\frac{1}{10}[/latex] is our missing value.

Thus, our answer is [latex]\frac{4}{10}[/latex].
Take-Away Approach
Lay out the minuend (first number). We want to take away the subtrahend (second number).

We have seven pieces of size [latex]\frac{1}{10}[/latex] and need to remove three pieces of size [latex]\frac{1}{10}[/latex].

This leaves us with four pieces of size [latex]\frac{1}{10}[/latex].Thus, our answer is [latex]\frac{4}{10}[/latex].
Both of these models show that [latex]\frac{7}{10}-\frac{3}{10}=\frac{4}{10}[/latex].
Concept Check: Reconsider the missing-addend model used in Example 4. Is four pieces of size one-tenth the only thing we could have used to fill the gap?
Solution
No. Since [latex]\frac{4}{10}[/latex] is equivalent to [latex]\frac{2}{5}[/latex], we could also have use two pieces of size [latex]\frac{1}{5}[/latex]. Any fraction equivalent to [latex]\frac{4}{10}[/latex] will correctly fill in the missing space.

Let's consider a problem with our C-strips. As with addition, we need to identify which strip will represent a unit. Once we have all of our relevant pieces, we can use the missing addend model.
Example 5
Find the difference of [latex]\frac{7}{11}[/latex] and [latex]\frac{3}{11}[/latex] using C-strips.
- As in Example 2, since our denominator is [latex]11[/latex], the C-strip [latex]S[/latex] (with a length of [latex]11[/latex]) represents one unit. This gives [latex]K[/latex] (with a length of [latex]7[/latex]) representing [latex]\frac{7}{11}[/latex]; and [latex]L[/latex] (with a length of [latex]3[/latex]) representing [latex]\frac{3}{11}[/latex].
- Which C-strip represents the difference of [latex]K[/latex] and [latex]L[/latex]? Putting strip [latex]K[/latex] above strip [latex]L[/latex], we see that C-strip [latex]P[/latex] (length [latex]4[/latex]) is what needs to be added to strip [latex]L[/latex] to equal strip [latex]K[/latex].

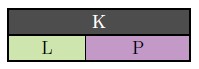
-
- Now that we know our answer is strip [latex]P[/latex] (length [latex]4[/latex]), we need to compare it to our unit strip, [latex]S[/latex] (length [latex]11[/latex]) to find it's value. Comparing strip [latex]P[/latex] to strip [latex]S[/latex] shows that [latex]P[/latex] has value [latex]\frac{4}{11}[/latex].
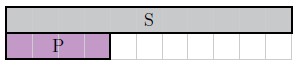
Example 5, shows that [latex]\frac{7}{11}-\frac{3}{11}=\frac{4}{11}[/latex]. What we see is that if fractions have the same denominator, they come from the same unit, so we can keep the denominator and just subtract the numerators. In general,
[latex]\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b}[/latex].
Exercise 3
Find the following differences using the physical manipulative listed.
a. [latex]\frac{7}{8}-\frac{3}{8}[/latex] (Fraction tiles)
Solution
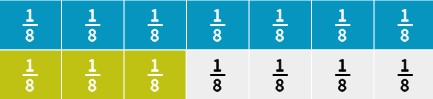
Answer: [latex]\frac{4}{8}[/latex]
The gap could also be filled by any fraction equivalent to [latex]\frac{1}{2}[/latex].
b. [latex]\frac{5}{7}-\frac{2}{7}[/latex] (C-strips)
Solution
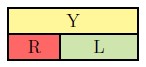

Answer: [latex]\frac{3}{7}[/latex]
c. [latex]\frac{11}{12}-\frac{7}{12}[/latex] (Fraction tiles or C-strips)
Solution
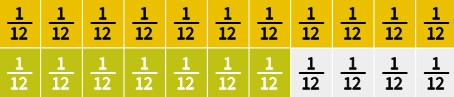
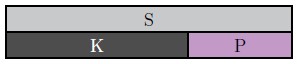

Answer: [latex]\frac{4}{12}[/latex] or [latex]\frac{1}{3}[/latex]
Subtraction of Fractions with Different Denominators
At this point, you may have guessed, if two fractions have different denominators, we need to convert them to the same unit/piece before we can subtract them. Our missing-addend model with fraction tiles is actually the only one that does not require we find a common denominator.
If we want to find [latex]\frac{11}{12}-\frac{1}{6}[/latex], we can line up the fraction tiles with [latex]\frac{1}{6}[/latex] underneath the eleven pieces of size [latex]\frac{1}{12}[/latex].
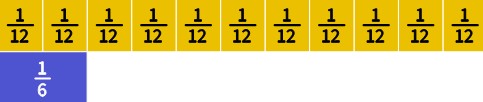
We need to know what can fill the gap. One tile that works are one-fourth pieces.

Thus, [latex]\frac{11}{12}-\frac{1}{6}=\frac{3}{4}[/latex].
Note that this is not the only tile we could have used. Both [latex]\frac{6}{8}[/latex] and [latex]\frac{9}{12}[/latex] would have worked since they are equivalent to [latex]\frac{3}{4}[/latex].
Fraction tiles are the easiest to use because they have a set unit size, and we work within that unit size, but this makes them inflexible. If we want to solve [latex]\frac{2}{3}-\frac{2}{5}[/latex], no combination of fraction tiles will work. We can, however, use our C-strips.
Example 6
Find the difference [latex]\frac{2}{3}-\frac{2}{5}[/latex] using C-strips.
Solution:
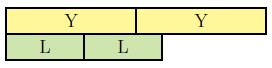
- First we need to determine what our unit size should be. It needs to be a multiple of [latex]3[/latex] and [latex]5[/latex], so let's consider [latex]15[/latex]. We don't have a C-strip of length [latex]15[/latex], but we can put together ten and five to make [latex]15[/latex]. The will be one [latex]O[/latex] strip and one [latex]Y[/latex] strip.
![]()
- Now that we have our unit, notice that [latex]\frac{1}{3}[/latex] can be represented by [latex]Y[/latex] (length [latex]5[/latex]) and [latex]\frac{1}{5}[/latex] can be represented by [latex]L[/latex] (length [latex]3[/latex]).


- Next we use missing addend on two [latex]Y[/latex] strips minus two [latex]L[/latex] strips, we find the difference to be one [latex]P[/latex] strip, which has length [latex]4[/latex].
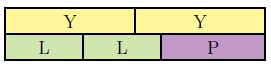
- When we compare [latex]P[/latex] to our unit, we see [latex]P[/latex] has size [latex]\frac{4}{15}[/latex].

Example 6 shows us [latex]\frac{2}{3}-\frac{2}{5}=\frac{10}{15}-\frac{6}{15}=\frac{4}{15}[/latex].
Let's see an example of subtraction with our dot model. Here, we will use the take-away model of subtraction.
Example 7
Use the dot model to do the following subtraction: [latex]\frac{3}{7} – \frac{2}{5}[/latex].
Solution:
Step 1: As with the addition, we take our denominators and make a [latex]5[/latex] by [latex]7[/latex] array of dots to be our unit. Since our unit has [latex]35[/latex] dots, each dot equals [latex]\frac{1}{35}[/latex].

Step 2: To see the value of a fifth, break our unit array into five equal pieces. There are five rows, so each row is [latex]\frac{1}{5}[/latex]. This means [latex]7[/latex] dots equals [latex]\frac{1}{5}[/latex].


Step 3: Similarly, we have [latex]7[/latex] equal columns, so each column is [latex]\frac{1}{7}[/latex] of a unit. This means [latex]5[/latex] dots equals [latex]\frac{1}{7}[/latex].


Step 4: Now that we know our whole and our unit fractions, we can determine the number of dots in [latex]\frac{2}{5}[/latex] and the number of dots in [latex]\frac{3}{7}[/latex].


Since each dot has a value of [latex]\frac{1}{35}[/latex], we have that [latex]\frac{2}{5}=\frac{14}{35}[/latex] and [latex]\frac{3}{7}=\frac{15}{35}[/latex]
Now, we subtract, using the take-away model.
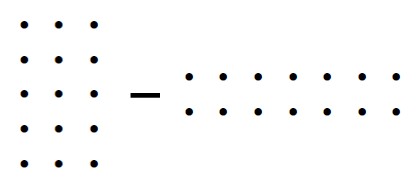
[latex]15[/latex] dots [latex]-[/latex] [latex]14[/latex] dots [latex]=[/latex] [latex]1[/latex] dot.
Answer: [latex]\frac{1}{35}[/latex]
In Example 7, we used the dot model to visualize: [latex]\frac{3}{7}-\frac{2}{5}=\frac{15}{35}-\frac{14}{35}=\frac{1}{35}[/latex].
Exercise 4
Find the following differences using the physical manipulatives listed. Be sure you can explain what is happening at every step in the process.
a. [latex]\frac{3}{4}-\frac{1}{3}[/latex] (Fraction tiles)
Solution
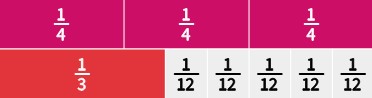
Answer: [latex]\frac{5}{12}[/latex]
b. [latex]\frac{2}{3}-\frac{1}{6}[/latex] (C-strips)
Solution
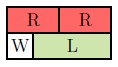
Answer: [latex]\frac{3}{6}[/latex] or [latex]\frac{1}{2}[/latex]
c. [latex]\frac{3}{4}-\frac{4}{7}[/latex] (Dot model)
Solution
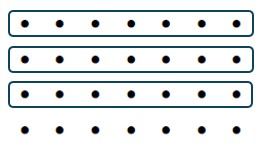
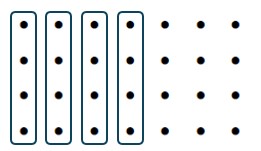
[latex]21[/latex] dots minus [latex]16[/latex] dots is [latex]5[/latex] dots of size [latex]\frac{1}{28}[/latex]
Answer: [latex]\frac{5}{28}[/latex]
Algorithm for Addition and Subtraction of Fractions - Common Denominator
This algorithm was covered in the Pre-Unit Review: Add and Subtract Fractions. This is one of the most forgotten algorithms, so now that you can visualize adding and subtracting fractions, let's revisit this topic.
Mathematically, what was done above is to write the two fractions into their equivalent forms with a common denominator, then add or subtract the numerators. This is because, in order to add or subtract fractions that do not have a common denominator, we must first rewrite each fraction as an equivalent fraction so that both fractions have a common denominator. As numbers in the denominator get larger, it is not feasible to draw out dots or use C-strips. Thus, it is important for children to understand the physical models deeply enough to move beyond them to an algorithm with numbers.
The easiest way to find a common denominator is to convert each fraction to an equivalent fraction using the other fraction's denominator. Consider the fractions [latex]\frac{4}{9}[/latex] and [latex]\frac{5}{12}[/latex]. If we want a common denominator, we can convert each fraction as follows:
[latex]\frac{4}{9}=\frac{4\times 12}{9\times 12}=\frac{48}{108}[/latex]
[latex]\frac{5}{12}=\frac{5\times 9}{12\times 9}=\frac{45}{108}[/latex]
Now we have two fractions of the same denominator and can add, subtract, and compare as desired. For example, [latex]\frac{4}{9}+\frac{5}{12}[/latex] is
[latex]\frac{4}{9}+\frac{5}{12}=\frac{48}{108}+\frac{45}{108}=\frac{93}{108}[/latex].
Unless the context makes sense otherwise, we do not like to leave our answer as an unsimplified fraction. Simplifying [latex]\frac{93}{108}[/latex] gives
[latex]\frac{93}{108}=\frac{31\times 3}{36\times 3}=\frac{31}{36}[/latex].
Concept Check:
a. Is [latex]108[/latex] the smallest denominator [latex]\frac{4}{9}[/latex] and [latex]\frac{5}{12}[/latex] have in common?
Solution
No it is not. The least common multiple of the two numbers will be the smallest common denominator. Since, [latex]LCM(9,12) = 36[/latex], [latex]36[/latex] is the smallest common denominator for [latex]\frac{4}{9}[/latex] and [latex]\frac{5}{12}[/latex].
b. If you use the least common denominator, will you ever need to simplify your answer?
Solution
Occasionally, yes. Consider [latex]\frac{2}{3}-\frac{1}{6}[/latex]. The least common multiple of [latex]3[/latex] and [latex]6[/latex], is [latex]6[/latex]. Converting our fractions gives
[latex]\frac{2\times 2}{3\times 2}-\frac{1}{6}=\frac{4}{6}-\frac{1}{6}=\frac{3}{6}[/latex].
But [latex]\frac{3}{6}[/latex] is not in simplest form. The simplest form of [latex]\frac{3}{6}[/latex] is [latex]\frac{1}{2}[/latex].
To be fair, this does not happen often. The majority of the time, if you use the least common denominator, you will not need to simplify your fraction.
If finding the least common multiple of the denominators is too time-consuming, you can always fall back on the "multiply by the other denominator" technique.
Common Denominator Algorithm for Adding and Subtracting Fractions
Let [latex]a[/latex], [latex]b[/latex], [latex]c[/latex], and [latex]d[/latex] be numbers such that [latex]b\not = 0[/latex] and [latex]d\not = 0[/latex]. Then
[latex]\displaystyle\frac{a}{b} + \frac{c}{d} = \frac{ad}{bd} + \frac{bc}{bd} = \frac{ad + bc}{bd}[/latex] and
[latex]\displaystyle\frac{a}{b} - \frac{c}{d} = \frac{ad}{bd} - \frac{bc}{bd} = \frac{ad - bc}{bd}[/latex].
Exercise 5
Solve the following addition and subtraction problems using the common denominator algorithm. Be sure to simplify your answer.
a. [latex]\frac{5}{21} + \frac{3}{7}[/latex]
Solution
[latex]LCM(21, 7) = 21[/latex]
[latex]\frac{5}{21} + \frac{3\times 3}{7\times 3}=\frac{5}{21} + \frac{9}{21 }= \frac{14}{21} = \frac{2}{3}[/latex]
b. [latex]\frac{14}{15} - \frac{5}{8}[/latex]
Solution
[latex]LCM(15, 8) = 120[/latex]
[latex]\frac{14\times 8}{15\times 8} - \frac{5\times 15}{8\times 15} = \frac{112}{120}-\frac{75}{120} = \frac{37}{120}[/latex]
c. [latex]\frac{1}{7} + \frac{4}{9}[/latex]
Solution
[latex]LCM(7, 9) = 63[/latex]
[latex]\frac{1\times 9}{7\times 9} + \frac{4\times 7}{9\times 7} = \frac{9}{63} + \frac{28}{63} = \frac{37}{63}[/latex]
d. [latex]\frac{14}{3} - \frac{5}{2}[/latex]
Solution
[latex]LCM(3, 2) = 6[/latex]
[latex]\frac{14\times 2}{3\times 2} - \frac{5\times 3}{2\times 3} = \frac{28}{6} - \frac{15}{6} = \frac{13}{6}=2\;\frac{1}{6}[/latex]
Estimation of Addition and Subtraction
It is important to practice number sense when it comes to fractions. If you enter the numbers incorrectly into your calculator and get a bad answer, you'll be able to catch it. Not only is it a good way to check your answer, but it will make you more comfortable with fractions whenever they come up in life!
Example 8
Estimate [latex]\frac{4}{9} + \frac{5}{12}[/latex].
Solution:
Notice that [latex]\frac{4}{9}[/latex] is a little less than [latex]\frac{1}{2}[/latex] and [latex]\frac{5}{12}[/latex] is also a little less than [latex]\frac{1}{2}[/latex].
This means the sum is a little less than [latex]\frac{1}{2} +\frac{1}{2} = 1[/latex]
When we solved this problem earlier, our answer was [latex]\frac{31}{36}[/latex]. This is close to our estimate of 1.
Exercise 6
Estimate the given sum or difference.
a. [latex]\frac{5}{21} + \frac{3}{7}[/latex]
Solution
[latex]\frac{5}{21}[/latex] is a little less than [latex]\frac{1}{4}[/latex].
[latex]\frac{3}{7}[/latex] is a little less than [latex]\frac{1}{2}[/latex].
The sum should be a little less than [latex]\frac{3}{4}[/latex] because that is [latex]\frac{1}{2} + \frac{1}{4}[/latex].
b. [latex]\frac{14}{15} - \frac{5}{8}[/latex]
Solution
[latex]\frac{14}{15}[/latex] is a little less than [latex]1[/latex].
[latex]\frac{5}{8}[/latex] is a little more than [latex]\frac{1}{2}[/latex].
The difference should be a little less than to [latex]1 - \frac{1}{2} = \frac{1}{2}[/latex].
A more accurate estimate would be to use [latex]\frac{2}{3}[/latex] for [latex]\frac{5}{8}[/latex]. Then our estimate of the difference is [latex]\frac{1}{3}[/latex].
c. [latex]\frac{1}{7} + \frac{4}{9}[/latex]
Solution
[latex]\frac{1}{7}[/latex] is close to [latex]0[/latex].
[latex]\frac{4}{9}[/latex] is close to [latex]\frac{1}{2}[/latex].
The sum should be close to [latex]0 + \frac{1}{2} = \frac{1}{2}[/latex].
d. [latex]\frac{14}{3} - \frac{5}{2}[/latex]
Solution
[latex]\frac{14}{3}[/latex] is a little less than to [latex]5[/latex].
[latex]\frac{5}{2}[/latex] is exactly to [latex]2\;\frac{1}{2}[/latex].
The difference should be a little less than [latex]5 - 2\;\frac{1}{2} = 2\;\frac{1}{2}[/latex].
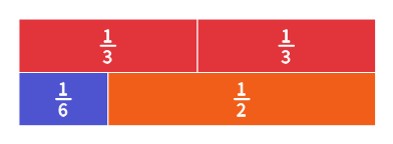
Classroom Connection: Your students are modeling [latex]\frac{2}{3}-\frac{1}{6}[/latex] with fraction tiles.
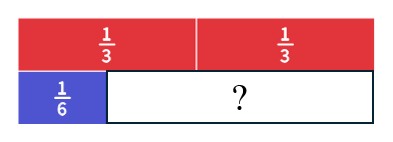
Penny gives the following model.
Answer: [latex]\frac{1}{2}[/latex]
Penny is confused about how the answer can be [latex]\frac{1}{2}[/latex] since [latex]2[/latex] is not a common multiple for [latex]3[/latex] and [latex]6[/latex]. She says the answer must have a denominator that is a multiple of [latex]3[/latex] and [latex]6[/latex]. What do you tell her?
Solution
You can find the answer using a common denominator, but sometimes that answer can be simplified. In this case, if you use the sixth tiles, you would get an answer of [latex]\frac{3}{6}[/latex] or if you use the twelfth tiles, you would get an answer of [latex]\frac{6}{12}[/latex]. These are both the same number as [latex]\frac{1}{2}[/latex].
Applications of Addition and Subtraction of Fractions
Adding and subtracting fractions is part of everyday life. The key with word problems is to understand what is happening and use a model to mimic the action. Since we are dealing with something real, it is easier to imagine what is going on.
Example 9
Use a visual fraction model to solve the following word problem.
A bakery sells donuts, scones, and cookies. The display case is split into five equal sections. If two sections are filled with donuts and one section is filled with scones, what fraction of the display case is filled with cookies?
Solution:
First, let's draw the display case with five equal spaces.
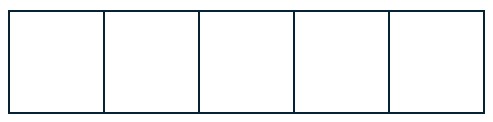
Second, let's label what we know.
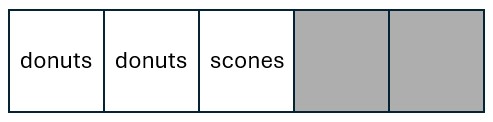
We have filled [latex]3[/latex] of the [latex]5[/latex] spaces, leaving [latex]2[/latex] spaces leftover. Since cookies are the only good left, those [latex]2[/latex] spaces must be for cookies.
Answer: [latex]\frac{2}{5}[/latex]
Exercise 7
Use a visual model to solve the following word problems.
- The local animal shelter is holding an adoption event. They have four categories of animals up for adoption: small dogs, big dogs, kittens, and cats. If one-fourth of the animals adopted were kittens, one-half were small dogs, and one-eighth were big dogs, what fraction were cats?
- Julian is making chicken alfredo and baking a cake. If the alfredo calls for [latex]1\; \frac{3}{4}[/latex] a cup of milk and the cake needs [latex]\frac{2}{3}[/latex] a cup of milk, how much milk does Julian need?
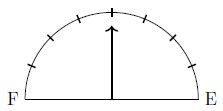
- It takes[latex]\frac{5}{8}[/latex] of a tank of gas for Madeline to drive to visit her grandmother. If her gas gauge looks like the image below, how much more gas does she need to make it to her grandmother's house?
- It takes 4 bags of mulch to cover the flower bed at the park. There are five partial bags in the shed. Bag one is half full. Bag two is [latex]\frac{2}{3}[/latex] full. Bag three is [latex]\frac{5}{6}[/latex] full. Bags four and five are completely full. Do they have enough mulch? If so, how much extra do they have? If not, how much more do they need?
