41 Module 9.1 Concept of Fraction
Louisiana Student Standards
Standard Number |
Description of Standard |
| 3.NF.3. | Explain the equivalence of fractions with denominators [latex]2, 3, 4, 6[/latex] and [latex]8[/latex] in special cases, and compare fractions by reasoning about their size.
|
| 4.NF.A. | Extend understanding of fraction equivalence and ordering.
|
1. Understanding Fractions with C-Strips
Usually, a fraction is defined as a number that can be written as the quotient (ratio) of an integer, [latex]m,[/latex] and a nonzero integer, [latex]n,[/latex] that is, [latex]\frac{m}{n}.[/latex] In this form, the dividend [latex]m[/latex] is called the numerator and the divisor [latex]n[/latex] is called the denominator. In reality, a fraction is often used as a stand-alone number with its own value, rather than just as a result associated with the operation among two other numbers (that is, the division of [latex]m[/latex] divided by [latex]m[/latex]. This warm-up activity aims to review the concept of fractions using C-strip (see in Figure 9-1). Hereafter, we use the capital letters to represent the strips as shown in Figure 9-1.
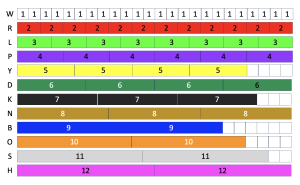
Before we represent fractions using C-strips, let’s recall that the denominator of a fraction indicates how many equal parts make up [latex]1[/latex] whole unit, while the numerator tells you how many of those equal parts are being considered. For example, to represent the fraction [latex]\frac{2}{5}[/latex] the denominator "[latex]5[/latex]" shows that we should divide up the 1 whole unit into 5 equal parts, whereas the numerator indicates that 2 out of the 5 will be considered. Using C-strips helps students to visualize these terms as shown in the example below.
Example 1
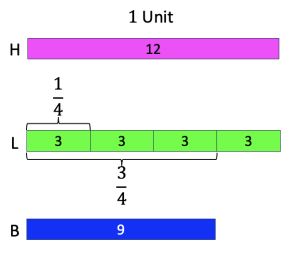
If H (hot pink) represents [latex]1[/latex] unit, then which C-strip represents [latex]\frac{3}{4}[/latex]?
Solution:
Let's consider the following steps to answer the question.
a. The denominator is 4; so it takes 4 equal parts to make one unit, and each of those 4 equal parts [latex]= \frac{1}{4}[/latex].
b. Find the C-strip such that a train of 4 of them is as long as one unit (H). Since a train of 4 light green C-strips (L) is the length of H (1 unit), then each light green C-strip makes up one part of a whole.
c. This means each light green C-strip represents [latex]\frac{1}{4}[/latex].
d. To find which C-strip represents [latex]\frac{3}{4}[/latex], we make a train of 3 light green C-strips.
e. Find the C-strip having the same length of the train of the 3 light green C-strips. This would be the Blue (B) C-strip.
Therefore, the answer is B, the Blue C-strip, as shown in Figure 9-1.
Example 1 above is solved following the sequence of steps from a. to e.:
a. Look at the denominator of the given fraction, and state how many unknown C-strips (that is, equal parts) make up the given C-strip representing 1 whole unit.
b. State what is the unknown C-strip that we can use to make up the given C-strip as 1 whole unit.
c. State the fraction that one C-strip found in b. represents, which is called a unit fraction.
d. Look at the numerator of the given fraction, and state how many C-strips in b. We need to build a "train" to represent it.
e. State which C-strip has the same length as the train built in d., and this is the answer.
After completing the five steps, we found that, if H (the Hot Pint C-strip) represents 1 unit, then B (the Blue C-strip) represents [latex]\frac{3}{4}[/latex]. The five-step process helps students unpack the meaning of denominator and numerator step by step. We may shorten the solution of Example 1 as
a. [latex]4[/latex] b. L c. [latex]\frac{1}{4}[/latex], or "one fourth" d. [latex]3[/latex] e. B
Exercises 1-6 provide more practice similar to Example 1.
Exercises 1-6
For exercises 1 - 6, explain how to find the solution. Do each step from a. to e. using your C-strips and record your answer for each step in the blank accordingly.
a. State how many C-strips (each an equal part of the whole) make up one unit.
b. State which C-strip makes up one part of the whole.
c. State the fraction that the C-strip in part b represents.
d. State how many of the C-strips in part b you need to make into a train.
e. State which C-strip is the length of the train you made in part c, this is the answer!!!
1. If H represents 1 unit, then which C-strip represents [latex]\frac{5}{6}[/latex]?
2. If H represents 1 unit, then which C-strip represents [latex]\frac{5}{12}[/latex]?
3. If O represents 1 unit, then which C-strip represents [latex]\frac{2}{5}[/latex]?
4. If B represents [latex]1[/latex] unit, then which C-strip represents [latex]\frac{2}{3}[/latex]?
5. If D represents [latex]1[/latex] unit, then which C-strip represents [latex]\frac{5}{3}[/latex]?
6. If N represents 1 unit, then which C-strip represents [latex]\frac{3}{4}[/latex]?
If N (brown) represents [latex]\frac{4}{5}[/latex], then which C-strip represents 1 unit?
Solution:
We consider the following steps to answer the question.
a. The denominator is 5, so it takes 5 equal parts to make up 1 whole unit, where each equal part is [latex]\frac{1}{5}[/latex]. Since N is only [latex]\frac{4}{5}[/latex], then a train of only 4 of the 5 equal parts will be the length of N.
b. A train of 4 red C-strips is the same length as N. So a red C-strip is one of the 5 equal parts that make up a whole.
c. Since it takes 5 equal parts (5reds) to make one unit, each red strip represents [latex]\frac{1}{5}[/latex].
d. And we form a train of 5 reds and see which C-strip has this length.
e. A train of 5 reds has the same length as the orange C-strip (O).
Therefore, the answer is O.
So, the solution includes (a.) looking at numerator, which indicates how many equal parts are in the given C-strip; (b.) figuring out which C-strip represents 1 equal part of the whole; (c) recognizing the unit fraction that the C-strip in (b) represents; (d.) recognizing how many C-strip we found in b. can make a whole according to the denominator; and, lastly, (e.) finding the length of the whole and the C-strip that represents it. Similarly to what we did for Example 1, the solution of Example 2 may be shortened as
a. 4 b. R c. [latex]\frac{1}{5}[/latex] , or "one fifth" d. 5 e. O
Exercises 7-11 provide more practice for Example 2.
Exercises 7-11
For exercises 7 - 11, explain how to find the solution. Do each step using your C-strips and record your answer for each step in the blank accordingly.
a. State how many C-strips will make up the named C-strip stated in the problem. Look at the numerator.
b. Which C-strip makes up one equal part?
c. State the fraction that the C-strip in part b represents. Look at the denominator.
d. State how many of the C-strips in part b will make up one unit.
e. Form the unit by making a train from the equal parts (C-strip in part b) and state which C-strip has the same length as that train.
7. If D represents [latex]\frac{1}{2}[/latex], then which C-strip is 1 unit?
8. If L represents [latex]\frac{1}{3}[/latex], then which C-strip is 1 unit?
9. If P represents [latex]\frac{2}{3}[/latex], then which C-strip is 1 unit?
10. If N represents [latex]\frac{4}{5}[/latex], then which C-strip is 1unit?
11. If R represents [latex]\frac{2}{5}[/latex], then which C-strip is 1 unit?
The type of problems in Example 3 is a little more challenging. They take more steps. From the first piece of information, figure out which C-strip is the whole unit – just like you did in problems 7 - 11. Then, start over using that unit C-rod, and figure out the second part of the question – just like you did in problems 1 - 6.
Example 3
If N represents [latex]\frac{2}{3}[/latex], then which C-strip represents [latex]\frac{3}{4}[/latex]?
Solution:
We consider the following steps to answer the question.
a. Begin these the same way the previous problems were done by first figuring out what the unit C-strip is. After doing the same steps you did for exercises 1-6, you will conclude that H is the unit C-strip.
b. Now, on to part 2: Start over with H as the unit C-strip, and find [latex]\frac{3}{4}[/latex] the same way you did it for the first 13 exercises. The key is to start over by looking only at the stated unit C- strip (H in this case), and not getting that confused with the first part of the problem. In other words, now that you have determined that the unit is H, determine what is [latex]\frac{3}{4}[/latex] (in relation to the unit - H). You will find that the answer is B.
Exercises 12-14 provide more practice for Example 3.
Exercises 12-14
12. If P represents [latex]\frac{2}{3}[/latex], then which C-strip represents [latex]\frac{3}{2}[/latex]?
13. If O represents [latex]\frac{5}{6}[/latex], then which C-strip represents [latex]\frac{3}{4}[/latex]?
14. If D represents [latex]\frac{2}{3}[/latex], then which C-strip represents [latex]\frac{1}{3}[/latex]?
2. Representing Fractions
Some commonly used representations to visualize fractions are the set model, bar model, area model, and number line model. Below are several examples showing how fractions can be represented using these methods.
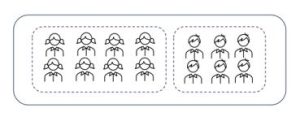
Figure 9-5 represents a class of 14 students as a set with two subsets, one of which includes 8 girls and the other 6 boys. It shows [latex]\frac{8}{14}[/latex] of the class are girls and [latex]\frac{6}{14}[/latex] of the class are boys.
The bar model below (Figure 9-6) represents [latex]\frac{4}{6}[/latex], in which the whole bar is divided into 6 equal parts with 4 of them shaded.

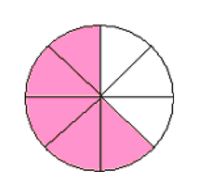
The circle below (Figure 9-7) is evenly divided into 8 parts, and five of them are shaded to represent [latex]\frac{5}{8}[/latex] by an area model. An area model may be in a square or rectangle as well.
A fraction as a number has its unique value, so that it can be represented on a number line according to its value. This is the so-called number line model (as shown in Figure 9-8).

There are also other manipulatives for hands-on activities that are helpful in fostering students’ understanding of fractions, such as fraction tiles, fraction bars, colored rods, pattern blocks, and tangrams etc.
Exercises 15-17
For Exercises 15-17, fill in the blanks using appropriate fractions represented by the models.
15. The unshaded portion is _______ of the whole figure below.

Solution
The unshaded portion is [latex]\frac{2}{5}[/latex] of the whole figure.
16. The shaded portion is _____ of the whole square. The unshaded portion is ______ of the whole square.
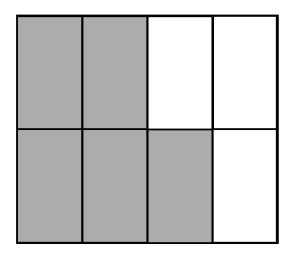
Solution
The shaded portion is [latex]\frac{5}{8}[/latex] of the whole square. The unshaded portion is [latex]\frac{3}{8}[/latex] of the whole square.
17. The shaded portion is _____ of the whole circle. The unshaded portion is ______ of the whole circle. The unshaded portion is _______ of the half circle.
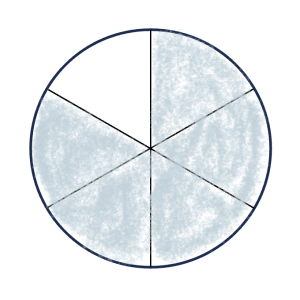
Solution
The shaded portion is [latex]\frac{5}{6}[/latex] of the whole circle. The unshaded portion is [latex]\frac{1}{6}[/latex] of the whole circle. The unshaded portion is [latex]\frac{1}{3}[/latex] of the half circle.
3. Equivalent Fractions
Before we move on to discuss equivalent fractions, let's do a brief review on the definition of rational numbers. A rational number is simply the formal name for a fraction.
Definition - Rational Number
A rational number is a number that can be written as the quotient of an integer, [latex]m[/latex], and a nonzero integer, [latex]n[/latex], which is written as [latex]\frac{m}{n}[/latex]. When written in this form, [latex]m[/latex] is called the numerator and [latex]n[/latex] is called the denominator. If [latex]GCF(m, n)=1[/latex] (i.e., [latex]m[/latex] and [latex]n[/latex] have no factors in common), then the rational number is said to be in its simplest form, or reduced form.
The following is another way to represent a rational number, [latex]\frac{m}{n}[/latex].
Divide a (defined) unit into an equal number of [latex]n[/latex] parts or subsets, which means [latex]n[/latex] parts make up a whole. Each one of these parts (or subsets) represents [latex]\frac{1}{n}[/latex], called a unit fraction. Then, [latex]m[/latex]of those parts represents [latex]\frac{m}{n}[/latex]. That is,
[latex]\frac{m}{n}=m \times \frac{1}{n}[/latex]
Two fractions that represent the same number are called equivalent fractions.
In Example 4, we use dot models (arrays of dots) to represent equivalent fractions.
Example 4
For each rational number [latex]\frac{m}{n}[/latex], complete Part a and Part b stated below.
a. Define a unit in terms of dots. State the value of each dot. Then complete these three steps one by one.
i. Divide the unit into an equal number (the denominator) of parts.
ii. Show a representation of [latex]\frac{1}{n}[/latex].
iii. Show a representation of [latex]\frac{m}{n}[/latex].
b. Define the unit differently, and do the three steps (i, ii and iii) again.
Consider two fractions (1) [latex]\frac{3}{8}[/latex] and (2) [latex]\frac{2}{5}[/latex].
Solution:
(1) For [latex]\frac{3}{8}[/latex] :
a. Let one unit be defined by [latex]8[/latex] dots, as shown below. Each dot [latex]=\frac{1}{8}[/latex] .

i. The unit is divided into 8 equal parts, as shown below.
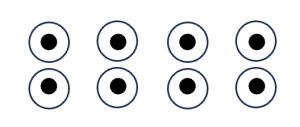
ii. Below is a representation of [latex]\frac{1}{8}[/latex], which is one of the equal parts shown in part i.
![]()
iii. Below is a representation of [latex]\frac{3}{8}[/latex].
![]()
b. Let one unit be defined by [latex]16[/latex] dots, as shown below. Each dot [latex]=\frac{1}{16}[/latex].

i. The unit is divided into [latex]8[/latex] equal parts, as shown below.

ii. Below is a representation of [latex]\frac{1}{8}[/latex], which is one of the equal parts shown in part b.
![]()
iii. Below is a representation of [latex]\frac{3}{8}[/latex].
![]()
Example 4 (Continued)
(2) For [latex]\frac{2}{5}[/latex],
a. Define a unit in terms of dots. State the value of each dot. Then complete these three steps one by one.
i. Divide the unit into an equal number (the denominator) of parts.
ii. Show a representation of [latex]\frac{1}{n}[/latex].
iii. Show a representation of [latex]\frac{m}{n}[/latex].
b. Define the unit differently, and do the three steps (i, ii and iii) again.
Solution:
(2) For [latex]\frac{2}{5}[/latex]
a. Let one unit be defined by 5 dots, as shown below. Each dot =[latex]\frac{1}{5}[/latex] .
![]()
i. The unit is divided into 5 equal parts, as shown below.

ii. Below is a representation of [latex]\frac{1}{5}[/latex], which is one of the equal parts shown in part b.
![]()
iii. Below is a representation of [latex]\frac{2}{5}[/latex].
![]()
b. Let one unit be defined by 10 dots, as shown below. Each dot = [latex]\frac{1}{10}[/latex].

i. The unit is divided into 5 equal parts, as shown below.
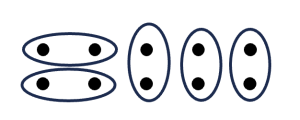
ii. Below is a representation of [latex]\frac{1}{5}[/latex], which is one of the equal parts shown in part b.
![]()
iii. Below is a representation of [latex]\frac{2}{5}[/latex].
![]()
Notice there are 2 dots for the answer in part a, where each dot represents [latex]\frac{1}{5}[/latex]. So, the 2 dots represent the number [latex]\frac{2}{5}[/latex]. For part b, the answer has 4 dots. Since each dot represents [latex]\frac{1}{10}[/latex], this also represents[latex]\frac{4}{10}[/latex] Therefore, [latex]\frac{2}{5}[/latex] and [latex]\frac{4}{10}[/latex] represent the same number. In other words, [latex]\frac{2}{5}[/latex] and [latex]\frac{4}{10}[/latex] are equivalent fractions.
By using dot models, students may notice that the same fraction can represent different quantities of dots, depending on how many dots make up the whole unit. Therefore, it is crucial to define the unit before beginning any exercise involving dot models.
Exercises 18-21 (Answers may vary on these exercises.)
18. Use the method in the last example to show two different representations for [latex]\frac{3}{4}[/latex].
19. Use your fraction arrays to determine all fractions on the fraction array that are equivalent to [latex]\frac{1}{2}[/latex]. Do this by finding [latex]\frac{1}{2}[/latex] on the array, and seeing what other numbers are the same length.
20. Use your fraction arrays to determine all fractions on the fraction array that are equivalent to[latex]\frac{2}{3}[/latex] Do this by finding [latex]\frac{2}{3}[/latex] on the array, and seeing what other numbers are the same length.
21. Write five equivalent fractions for each fraction given:
a. [latex]\frac{2}{3}[/latex] b. [latex]\frac{5}{7}[/latex] c. [latex]\frac{3}{8}[/latex]
Now we introduce the fundamental law of fractions, which is followed by two theorems on equivalent fractions and examples, respectively.
Key Takeaway-The Fundamental Law of Fractions
For any rational number a/b and any nonzero integer c, [latex]\frac{a}{b}[/latex]=[latex]\frac{ac}{bc}[/latex].
In other words, multiplying both the numerator and denominator by the same nonzero number does not change the value of the fraction.
The two fractions [latex]\frac{a}{b}[/latex]and [latex]\frac{ac}{bc}[/latex] are equivalent fractions.
According to the fundamental law of fractions, if both the numerator and the denominator of a fraction are multiplied by the same factor, the resulting fraction is equivalent to the original one. The ability to write a fraction in an equivalent form—with a different denominator but the same value—is a critical skill when performing addition and subtraction of fractions.
Example 5
Write the given fraction into its equivalent form with the notified denominator.
a. [latex]\frac{3}{4}[/latex] as a fraction with the denominator 20.
Solution:
To write [latex]\frac{3}{4}[/latex] as a fraction with the denominator 20, we multiply the original denominator 4 by the factor 5.
Then to keep the fraction equivalent to the original one, we should do the same operation to the original numerator:
multiplying it by the same factor 5: [latex]3\times 5=15[/latex].
In summary, we can write the solution as:
[latex]\frac{3}{4}= \frac{3\times 5}{4\times 5}=\frac{15}{20}[/latex].
b. [latex]\frac{5}{8}[/latex]as a fraction with the denominator 32.
Solution:
To write [latex]\frac{5}{8}[/latex] as a fraction with the denominator 32, we multiply the original denominator 8 by the factor 4.
Then to keep the fraction equivalent to the original one, we should do the same operation to the original numerator:
multiplying it by the same factor 3: [latex]5\times 4=20[/latex].
In summary, we can write the solution as:
[latex]\frac{5}{8}= \frac{5\times 4}{8\times 4}=\frac{20}{32}[/latex].
Below are more exercises to practice the skill in Example 5.
Exercises 22-24
Write the given fraction into its equivalent form with the notified denominator.
22. Write [latex]\frac{3}{5}[/latex] as (i) a fraction with the denominator 25, and (ii) a fraction with the denominator of 60.
Solution
(i) [latex]\frac{3}{5}= \frac{3\times 5}{5\times 5}=\frac{15}{25}[/latex]
(ii) [latex]\frac{3}{5}= \frac{3\times 12}{5\times 12}=\frac{36}{60}[/latex]
23. Write [latex]\frac{2}{7}[/latex] as (i) a fraction with the denominator of 21 and (ii) a fraction with the denominator of 42.
Solution
(i) [latex]\frac{2}{7}= \frac{2\times 3}{7\times 3}=\frac{6}{21}[/latex]
(ii) [latex]\frac{2}{7}= \frac{2\times 6}{7\times 6}=\frac{12}{42}[/latex]
24. Write [latex]\frac{5}{9}[/latex] as (i) a fraction with the denominator of 27 and (ii) a fraction with the denominator of 63.
Solution
(i) [latex]\frac{5}{9}= \frac{5\times 3}{9\times 3}=\frac{15}{27}[/latex]
(ii) [latex]\frac{5}{9}= \frac{5\times 7}{9\times 7}=\frac{35}{63}[/latex]
The fundamental law also helps us to simplify a fraction into simplest form. Firstly, let's define what is a simplest form.
Definition - Fraction in Simplest Form
A fraction, [latex]\frac{a}{b}[/latex], is in its simplest (or reduced) form if [latex]GCF(a, b) = 1[/latex], meaning that the numerator and denominator have no common factors other than 1.
There are two common ways to rewrite a fraction in its simplest form—that is, to simplify a fraction. One method is to use prime factorization: factor both the numerator and the denominator into primes, then cancel out any common factors. Another method involves using the greatest common factor (GCF) of the numerator and denominator. This process includes three steps:
(i) find the GCF of the numerator and denominator,
(ii) rewrite both numbers as the product of the GCF and another factor, and
(iii) cancel the common factor.
Even when all common factors are canceled from the numerator or denominator, a factor of 1 remains—it's just often not shown explicitly.
Example 6
Write [latex]\frac{315}{350}[/latex] in simplest form by using each of the two methods just described.
Solution:
Method 1: Prime factorization:
[latex]\frac{315}{350}=\frac{3\times3\times5\times7}{2\times5\times5\times7}=\frac{3\times3}{2\times5}=\frac{9}{10}[/latex]
Method 2: [latex]GCF(315, 350)[/latex] = [latex]35[/latex]:
[latex]\frac{315}{350}=\frac{9\times35}{10\times35}=\frac{9}{10}[/latex]
Exercise 25
Write each fraction in simplest form using each of the two methods: (1) prime factorization and (2) finding GCF as shown in the previous example. Show the actual factorization for each method, and then reduce to the simplest form.
a. [latex]\frac{378}{675}[/latex]
Solution
(1) prime factorization: [latex]\frac{378}{675}=\frac{2\times3\times3\times3\times7}{3\times3\times3\times5\times5}=\frac{2\times7}{5\times5}=\frac{14}{25}[/latex]
(2) [latex]GCF(378, 675) = 27[/latex], so [latex]\frac{378}{675}=\frac{14\times27}{25\times27}=\frac{14}{25}[/latex]
b. [latex]\frac{247}{323}[/latex]
Solution
(1) prime factorization: [latex]\frac{247}{323}=\frac{13\times19}{17\times19}=\frac{13}{17}[/latex]
(2) [latex]GCF(247, 323) = 19[/latex], so [latex]\frac{247}{323}=\frac{13\times19}{17\times19}=\frac{13}{17}[/latex]
The process of reducing fractions to their simplest forms can help us compare two or more fractions. Unlike whole numbers or integers, comparing fractions is not always straightforward. As we've seen in the Fundamental Law of Fractions and the examples above, two fractions with different denominators and different numerators can still represent the same value, which are called equivalent fractions.
Key Takeaways - Theorem I of Equivalent Fractions
Two fractions, [latex]\frac{a}{b}[/latex] and [latex]\frac{c}{d}[/latex], are equivalent if they simplify to the same fraction in simplest form.
Example 7
Determine if the following statements are true or false. State whether the pair of fractions are equivalent or not.
a. [latex]\frac{6}{8}=\frac{9}{12}[/latex]
Solution:
In simplest form, [latex]\frac{6}{8}=\frac{3}{4}[/latex] and [latex]\frac{9}{12}=\frac{3}{4}[/latex]. Therefore, [latex]\frac{6}{8}[/latex] and [latex]\frac{9}{12}[/latex] are equivalent.
b. [latex]\frac{15}{24}=\frac{10}{18}[/latex]
Solution:
In simplest form, [latex]\frac{15}{24}=\frac{5}{8}[/latex], and [latex]\frac{10}{18}=\frac{5}{9}[/latex]. Therefore, [latex]\frac{15}{24}[/latex] and [latex]\frac{10}{18}[/latex] are not equivalent.
Exercise 26
Determine if the following statements are true or false by writing each fraction in simplest form. State whether the pair of fractions are equivalent or not. Show your work and reasoning.
a. [latex]\frac{14}{25}=\frac{28}{50}[/latex]
Solution
[latex]\frac{28}{50}[/latex] reduces to [latex]\frac{14}{25}[/latex] and since [latex]\frac{14}{25}=\frac{14}{25}[/latex], then [latex]\frac{14}{25}[/latex] and [latex]\frac{28}{50}[/latex] are equivalent
b. [latex]\frac{25}{35}=\frac{10}{14}[/latex]
Solution
[latex]\frac{25}{35}[/latex] reduces to [latex]\frac{5}{7}[/latex] and [latex]\frac{10}{14}[/latex] reduces to [latex]\frac{5}{7}[/latex], so [latex]\frac{25}{35}[/latex] and [latex]\frac{10}{14}[/latex] are equivalent
c. [latex]\frac{12}{16}=\frac{25}{40}[/latex]
Solution
[latex]\frac{12}{16}[/latex] reduces to [latex]\frac{3}{4}[/latex] and [latex]\frac{25}{40}[/latex] reduces to [latex]\frac{5}{8}[/latex], so [latex]\frac{14}{25}[/latex] and [latex]\frac{28}{50}[/latex] are not equivalent
Key Takeaways - Theorem II of Equivalent Fractions
Assume [latex]a[/latex] and [latex]c[/latex] are whole numbers, and [latex]b[/latex] and [latex]d[/latex] are counting numbers. Two fractions, [latex]\frac{a}{b}[/latex] and [latex]\frac{c}{d}[/latex], are equivalent if and only if [latex]ad=bc[/latex].
That is,
[latex]\frac{a}{b}=\frac{c}{d} \Longleftrightarrow ad=bc[/latex]
In this theorem, the phrase if and only if, denoted by the symbol "[latex]\Longleftrightarrow[/latex]", means that the statement works in both directions: if [latex]ad=bc[/latex], then the two fractions, [latex]\frac{a}{b}[/latex] and [latex]\frac{c}{d}[/latex], are equivalent, and if the two fractions are equivalent, then [latex]ad=bc[/latex]. Using this method to determine whether two fractions are equivalent is called comparing cross products.
Example 8
Determine if the following statements are true or false by comparing cross products. State whether the pair of fractions are equivalent or not.
a. [latex]\frac{6}{8}=\frac{9}{12}[/latex]
Solution:
Since [latex]6 \times 12 = 8 \times 9[/latex], the statement is true. Therefore, [latex]\frac{6}{8}[/latex] and [latex]\frac{9}{12}[/latex] are equivalent fractions.
b. [latex]\frac{15}{24}=\frac{10}{18}[/latex]
Solution:
Since [latex]15 \times 18 ≠ 24 \times 10[/latex], the statement is false. Therefore, [latex]\frac{15}{24}[/latex] and [latex]\frac{10}{18}[/latex] are not equivalent fractions.
Exercise 27
Determine if the following statements are true or false by comparing cross products. State whether the pair of fractions are equivalent or not. Show your work and reasoning.
a. [latex]\frac{14}{25}=\frac{28}{50}[/latex]
Solution
By cross products:
[latex]14 \times 50 = 700[/latex] and [latex]25 \times 28 = 700[/latex]
Since [latex]700 = 700[/latex] then [latex]\frac{14}{25}[/latex] and [latex]\frac{28}{50}[/latex] are equivalent fractions.
b. [latex]\frac{25}{35}=\frac{10}{14}[/latex]
Solution
By cross products:
[latex]25 \times 14 = 350[/latex] and [latex]35 \times 10 = 350[/latex]
Since [latex]350 = 350[/latex] then [latex]\frac{35}{35}[/latex] and [latex]\frac{10}{14}[/latex] are equivalent fractions.
c. [latex]\frac{12}{16}=\frac{25}{40}[/latex]
Solution
By cross products:
[latex]12 \times 40 = 480[/latex] and [latex]16 \times 25 = 400[/latex]
Since [latex]480 ≠ 400[/latex] then [latex]\frac{12}{16}[/latex] and [latex]\frac{25}{40}[/latex] are not equivalent fractions.
4. Compare Rational Numbers
Each rational number—that is, each fraction—has its own value, just like other numbers such as whole numbers and integers. Therefore, we can compare two fractions based on their values. However, comparing fractions is not as straightforward as comparing whole numbers or integers, since a fraction’s value depends on both its numerator and its denominator. Pedagogically, it is helpful to introduce fraction comparison in stages: fractions with like denominators, fractions with like numerators, and fractions with unlike numerators and unlike denominators. These stages provide opportunities for students to develop a solid conceptual understanding on denominator and numerator, as well as the idea of equivalent fractions.
Comparing Fractions with Like Denominators
When two positive fractions have the same denominator, that common denominator indicates that both fractions are made up of the same kind of parts--each coming from a whole of the same size, divided into the same number of equal parts. The numerator of each fraction tells us how many of those equal parts the fraction includes. Therefore, the one with more parts (a larger numerator) must represent a greater quantity.
For example, in [latex]\frac{3}{8}[/latex] and [latex]\frac{5}{8}[/latex], both fractions describe quantities made up of eighths. Since [latex]5[/latex] eighths is more than [latex]3[/latex] eighths, [latex]\frac{5}{8} > \frac{3}{8}[/latex].
By rewriting both fractions as equivalent fractions with the same denominator, we make their parts the same size. Then we can compare the numerators directly. Mathematically, we express this as:
If [latex]a[/latex] is a non-zero whole number, [latex]b[/latex] and [latex]c[/latex] are whole numbers, then [latex]\frac{b}{a}>\frac{c}{a}[/latex] if, and only if, [latex]b>c[/latex].
Example 9
Compare [latex]\frac{2}{3}[/latex] and [latex]\frac{3}{5}[/latex].
Solution:
We rewrite both with a common denominator of 15:
[latex]\frac{2}{3} =\frac{2\times 5}{3\times 5} = \frac{10}{15}[/latex]
[latex]\frac{3}{5} = \frac{3\times 3}{5\times 3} =\frac{9}{15}[/latex]
Now since 10 parts are larger than 9 parts, [latex]\frac{10}{15} >\frac{9}{15}[/latex]
Therefore, [latex]\frac{2}{3} > \frac{3}{5}[/latex].
The practice of using a common denominator to compare fractions helps students master the skill of writing equivalent fractions and deepens their understanding of the meaning of denominators and numerators. It also gives students opportunities to practice clear and precise mathematical writing.
Comparing Fractions with Like Numerators
In contrast, when two positive fractions have the same numerator, they represent the same number of parts—but the size of each part depends on the denominator. The denominator tells us how many equal parts the whole is divided into. Therefore, a smaller denominator means fewer, larger parts, while a larger denominator means more, smaller parts.
Since both fractions have the same number of parts (same numerator), the one with the larger parts (i.e., the smaller denominator) represents a greater quantity. For example, in [latex]\frac{3}{5}[/latex] and [latex]\frac{3}{8}[/latex], both fractions include [latex]3[/latex] parts. But fifths are larger than eighths, so [latex]\frac{3}{5} > \frac{3}{8}[/latex].
In conclusion, among positive fractions with like numerators, the one with the larger denominator is smaller. Mathematically, we express this as:
If [latex]a[/latex] is a non-zero whole number, [latex]b[/latex] and [latex]c[/latex] are whole numbers, then [latex]\frac{b}{a}<\frac{c}{a}[/latex] if, and only if, [latex]b>c[/latex].
Example 10
Compare [latex]\frac{2}{3}[/latex] and [latex]\frac{3}{5}[/latex].
Solution:
We rewrite both with a common numerator of 6:
[latex]\frac{2}{3} =\frac{2\times 3}{3\times 3} = \frac{6}{9}[/latex]
[latex]\frac{3}{5} = \frac{3\times 2}{5\times 2} =\frac{6}{10}[/latex]
Now we have the same number of parts, but the sizes are different. Since one "whole" has 10 parts and the other "whole" has only 9 parts, each of the parts of the 10 are smaller than the ones in the 9. This means that: [latex]\frac{6}{9} >\frac{6}{10}[/latex].
Therefore, [latex]\frac{2}{3} > \frac{3}{5}[/latex].
While comparing with common numerators is a strategy that can be used, it's not always the easiest to use. Students are able to easily compare the number of parts, but have more trouble when it comes to comparing the sizes of the parts. Because of this, the two main strategies that are often used to compare them are using a common denominator and comparing cross products.
Comparing Cross Products
This method is also known as cross-multiplication. It avoids finding a common denominator explicitly and instead relies on comparing the cross products of the two fractions. Mathematically, we express this strategy as:
[latex]\frac{a}{b}\lt\frac{c}{d}\Longleftrightarrow ad\lt bc[/latex]
[latex]\frac{a}{b}>\frac{c}{d}\Longleftrightarrow ad>bc[/latex].
In a comparison like [latex]\frac{a}{b}<\frac{c}{d}[/latex], the first number ([latex]a[/latex]) and the last number ([latex]d[/latex]) are called the extremes. These are the outside numbers when the fractions are written side by side. The other two numbers, [latex]b[/latex] and [latex]c[/latex], are called the means, or the inside numbers. To compare the fractions, we multiply the extremes and the means and compare the resulting products.
Example 11
Compare the given fractions by comparing cross products.
-
- [latex]\frac{2}{5}[/latex] and [latex]\frac{3}{7}[/latex]
- [latex]\frac{6}{7}[/latex] and [latex]\frac{5}{6}[/latex]
Solution:
a. Multiply the extremes (2 and 7) and write the product on the left. Multiply the means (5 and 3) and write the product on the right:
[latex]2 \times 7 = 14[/latex] and [latex]5 \times 3 = 15[/latex]
Since [latex]14 < 15[/latex], we conclude that [latex]\frac{2}{5} < \frac{3}{7}[/latex].
b. Multiply the extremes (6 and 6) and put on the left. Multiply the means (7 and 5) and put on the right:
[latex]6 \times 6 = 36[/latex] and [latex]7 \times 5 = 35[/latex]
Since [latex]36 > 35[/latex], we conclude that: [latex]\frac{6}{7} > \frac{5}{6}[/latex].
The two methods--using a common denominator and comparing cross products--may seem unrelated at first glance, but they are mathematically equivalent--both rely on expressing the fractions in a comparable form to determine which is greater.
You may explore more on the connection between the two methods.
What’s the connection between using a common denominator and comparing cross products?
When you cross-multiply [latex]\frac{a}{b}[/latex] and [latex]\frac{c}{d}[/latex], you are essentially comparing:
[latex]a \times d[/latex] and [latex]b \times c[/latex].
But this is exactly what happens when you write both fractions with a common denominator of [latex]b \times d[/latex]:
[latex]\frac{a}{b} = \frac{a \times d}{b \times d}[/latex]
[latex]\frac{c}{d} = \frac{c \times b}{d \times b} = \frac{c \times b}{b \times d}[/latex]
Now both fractions have the same denominator, [latex]b \times d[/latex], and you compare the numerators [latex]a \times d[/latex] and [latex]b \times c[/latex].
So, comparing cross products is really a shortcut for rewriting both fractions with the same denominator—specifically, the product of the two original denominators.
Exercise 29
Use cross products to compare each of the following fractions. Use < or >.
a. [latex]\frac{4}{5}[/latex] and [latex]\frac{5}{8}[/latex]
Solution
[latex]4 \times 8 = 32[/latex] and [latex]5 \times 5 = 25[/latex]
Since [latex]32 > 25[/latex], then [latex]\frac{4}{5} > \frac{5}{8}[/latex].
b. [latex]\frac{12}{35}[/latex] and [latex]\frac{11}{18}[/latex]
Solution
[latex]12 \times 18 = 216[/latex] and [latex]35 \times 11 = 385[/latex]
Since [latex]216 < 385[/latex], then [latex]\frac{12}{35} < \frac{11}{18}[/latex].
c. [latex]\frac{13}{15}[/latex] and [latex]\frac{14}{17}[/latex]
Solution
[latex]13 \times 17 = 221[/latex] and [latex]15 \times 14 = 210[/latex]
Since [latex]221 > 210[/latex], then [latex]\frac{13}{15} > \frac{14}{17}[/latex].
Using Dot Models to Visualize Fraction Comparison
We are now going to work again with models, using dots, to compare two fractions. When you use dot models for each problem, it is CRUCIAL that you begin each problem by explicitly stating the following:
- Be specific about what you are using for the unit. It will be easiest if you use an array of dots, where the denominator of one fraction is the number of rows in the array, and the denominator of the other fraction is the number of columns in the array.
- State the value of each dot, each column, and each row.
Example 12
Use dot models to compare [latex]\frac{2}{5}[/latex] and [latex]\frac{3}{7}[/latex].
Solution:
Step 1: Let 1 unit = 5 rows of dots by 7 columns of dots, for a total of [latex]35[/latex] dots, as shown below. Since there are 35 dots to a unit, each dot = [latex]\frac{1}{35}[/latex] of a unit.

Step 2: Since there are 5 rows, the unit can be broken up into 5 equal parts by circling the rows, as shown below:

Therefore, each row is [latex]\frac{1}{5}[/latex] of a unit. Notice there are 7 dots in [latex]\frac{1}{5}[/latex] of a unit:
[latex]\frac{1}{5}=[/latex] ![]()
Step 3: Similarly, since there are 7 equal columns, each column is [latex]\frac{1}{7}[/latex] of a unit:

Therefore, [latex]\frac{1}{7}=[/latex] ![]() Step 4: Now that we have properly defined the unit, we are ready to show what [latex]\frac{2}{5}[/latex] looks like. Since [latex]\frac{1}{5}[/latex] is 1 row of dots, then [latex]\frac{2}{5}[/latex]must be [latex]2[/latex] rows of dots. Therefore, [latex]\frac{2}{5}[/latex] is shown below:
Step 4: Now that we have properly defined the unit, we are ready to show what [latex]\frac{2}{5}[/latex] looks like. Since [latex]\frac{1}{5}[/latex] is 1 row of dots, then [latex]\frac{2}{5}[/latex]must be [latex]2[/latex] rows of dots. Therefore, [latex]\frac{2}{5}[/latex] is shown below:

Notice that [latex]\frac{2}{5}[/latex] contains 14 dots, which is equivalent to [latex]\frac{14}{35}[/latex].
Step 5: Similarly, we can show what [latex]\frac{3}{7}[/latex] looks like. Since [latex]\frac{1}{7}[/latex] is 1 column of dots, then [latex]\frac{3}{7}[/latex]must be 3 columns of dots. Therefore, [latex]\frac{3}{7}[/latex] is shown below:

Notice that [latex]\frac{3}{7}[/latex] contains 15 dots, which is equivalent to [latex]\frac{15}{35}[/latex].
Since [latex]\frac{2}{5}[/latex] contains less dots than [latex]\frac{3}{7}[/latex], must be less than [latex]\frac{3}{7}[/latex]. That is, [latex]\frac{2}{5}[/latex] < [latex]\frac{3}{7}[/latex].
Note how to choose the dot array according to the common denominator of the two fractions.
Exercise 30
Compare [latex]\frac{3}{4}[/latex] and [latex]\frac{4}{5}[/latex] using models. Show all of the steps, and explain the procedure as shown in the previous example.
Solution
Step 1: Let 1 unit = 4 rows of dots by 5 columns of dots, for a total of 20 dots, as shown below. Since there are 20 dots to a unit, each dot = [latex]\frac{1}{20}[/latex] of a unit.

Step 2: There are 4 rows, so the unit can be broken up into 4 equal parts as shown below:
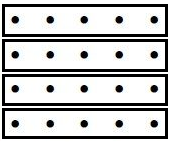
We can see that there are 5 dots in [latex]\frac{1}{4}[/latex] of a unit.
Step 3: Similarly, since there are 5 equal columns, each column is [latex]\frac{1}{5}[/latex] of a unit.

Now for this part we see there are 4 dots in [latex]\frac{1}{5}[/latex] of a unit.
Step 4: Now that we have properly defined the unit, we are ready to show what [latex]\frac{3}{4}[/latex] looks like. Since [latex]\frac{1}{4}[/latex] is [latex]1[/latex] row of dots, then [latex]\frac{3}{4}[/latex]must be [latex]3[/latex] rows of dots. Therefore, [latex]\frac{3}{4}[/latex] is shown below:
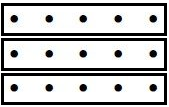
Or we can say that [latex]\frac{3}{4}[/latex] has 15 dots.
Step 5: Similarly, we can show what [latex]\frac{4}{5}[/latex] looks like. Since [latex]\frac{1}{5}[/latex] is 1 column of dots, then [latex]\frac{4}{5}[/latex]must be 3 columns of dots. Therefore, [latex]\frac{4}{5}[/latex] is shown below:

Here we can say that [latex]\frac{4}{5}[/latex] has 16 dots.
Since [latex]\frac{3}{4}[/latex] contains less dots than [latex]\frac{4}{5}[/latex], then [latex]\frac{3}{4}[/latex] < [latex]\frac{4}{5}[/latex].
Use Manipulatives to Compare Fractions
Manipulatives may be used to help students understand the comparison of fractions more solidly. Below is a set of activities that have the knowledge of comparing fractions embedded in.
Materials: Fraction Circles, Fraction Arrays, Multiple Strips, C-strips
Directions:
Use your marked fraction circles to do these first few activities.
1. Take one wedge from each fraction circle ([latex]\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{6},\frac{1}{7},\frac{1}{8},\frac{1}{9},\frac{1}{10}[/latex], and [latex]\frac{1}{12}[/latex]). One fraction is bigger than another if it covers more space than the other fraction. Compare them and put them in order from smallest to largest, and write them in order below, using the less than symbol ( < ).
2. From what you discovered in exercise 1, circle the larger fraction in each case.
a. [latex]\frac{1}{90}[/latex] or [latex]\frac{1}{95}[/latex] b. [latex]\frac{1}{32}[/latex] or [latex]\frac{1}{33}[/latex]
If you take 5 of the fraction pieces, each of which represents [latex]\frac{1}{8}[/latex], then together you have [latex]\frac{5}{8}[/latex]. Use this fact to do the next exercise.
3. Use the fraction circles to compare [latex]\frac{5}{8},\frac{5}{9},\frac{5}{10}[/latex], and[latex]\frac{5}{12}[/latex]. Put them in order from smallest to largest using the less than symbol ( < ).
4. From what you discovered in exercise 3, determine which is the larger fraction in each case.
a. [latex]\frac{15}{37}[/latex] or [latex]\frac{15}{40}[/latex] b. [latex]\frac{89}{100}[/latex] or [latex]\frac{89}{200}[/latex]
5. Use the fraction array to order these fractions: [latex]\frac{4}{5},\frac{4}{6},\frac{4}{7},\frac{4}{8},\frac{4}{9},\frac{4}{10},\frac{4}{11}[/latex], and [latex]\frac{1}{12}[/latex]. Put them in order from smallest to largest using the less than symbol ( < ).
6. Explain the pattern you learned from doing exercises 1-5.
7. Use fraction circles to compare these fractions:[latex]\frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{4}{5},\frac{5}{6},\frac{7}{8},\frac{8}{9},\frac{9}{10}[/latex], and [latex]\frac{11}{12}[/latex]. Put them in order from smallest to largest using the less than symbol ( < ).
8. Use the fraction array to order these fractions: [latex]\frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{4}{5},\frac{5}{6},\frac{7}{8},\frac{8}{9},\frac{9}{10}[/latex], and [latex]\frac{11}{12}[/latex]. Put them in order from smallest to largest using the less than symbol ( < ).
9. From what you discovered in exercises 7 and 8, determine which is the larger fraction in each case.
a. [latex]\frac{89}{90}[/latex] or [latex]\frac{94}{95}[/latex] b. [latex]\frac{56}{57}[/latex] or [latex]\frac{31}{33}[/latex]
10, Order these fractions: [latex]\frac{45}{46}, \frac{71}{72}, \frac{34}{35}, \frac{99}{100}, \frac{25}{26}, \frac{13}{14}[/latex], and [latex]\frac{51}{52}[/latex]. Put them in order from smallest to largest using the less than symbol ( < ).
11. Explain the pattern you learned from doing exercises 7 - 10.
12. Draw a model of your own that would help to convince someone why [latex]\frac{4}{5}[/latex] was bigger than [latex]\frac{2}{3}[/latex].
