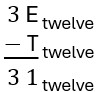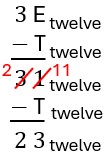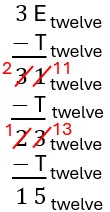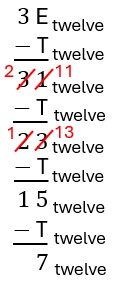29 Division Algorithms
Louisiana Student Standards for Mathematics
| 6.NS.2 | Fluently divide multi-digit numbers using the standard algorithm. |
You will need: Base Blocks (Material Cards 3-15)
There are two main algorithms for division: one based on partitioning by subsets and the other based on repeated subtraction. These algorithms are just the numerical version of what is done with base blocks.
Partitioning by Subsets Model and Long Division (Standard) Algorithm
Exploration Activity
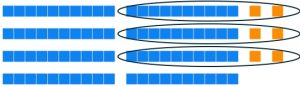
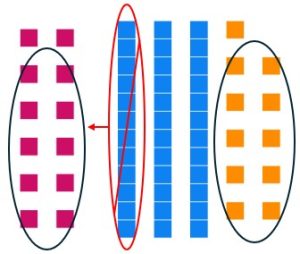
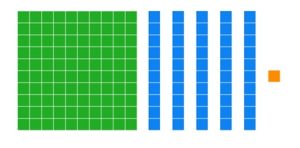
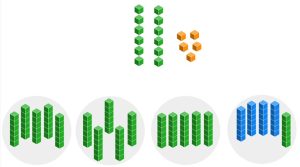
Pull out your base ten blocks. We will solve the base ten division problem [latex]151\div 4[/latex] using partitioning into subsets.
a. Lay out 151 in your base ten blocks.
b. We need to partition these into 4 subsets, so draw 4 empty circles.
c. Divide the blocks as evenly as possible between the 4 circles. (You should have 3 unit pieces leftover.)
We know that the answer to partitioning into subsets is the number of items in a subset. Each subset has 3 longs and 7 units and there are 3 units that were not put into any subset. In other words, each group has a value of 37 with 3 leftover. The answer is 37 remainder 3.
Using blocks to solve [latex]151 \div 4[/latex] is reasonable, but it is not reasonable to use blocks to solve things like [latex]146,573\div 5[/latex]. We need to take the process we do with the blocks and translate that into an algorithm using numbers.
Understanding Long Division
| Action with Base Ten Blocks | Matching Action in Long Division |
 |
|
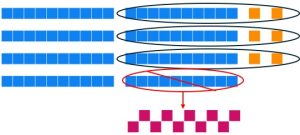
| Let's start by looking at how you distributed your blocks in the exploration activity. The one flat cannot be evenly distributed in its current form, so we need to break it into 10 longs. This gives us a total of 15 longs and one unit. | In terms of long division, we say "4 cannot go into 1" so we look at the number 150 instead of 100. Basically, we are saying one thing of size 100 does not work for partitioning the pieces, so we consider 15 things of size 10. |
 |
 |
| Next, we distribute 12 of the 15 longs into the 4 circles. | Because [latex]4\times 4[/latex] is more than 15, and [latex]4\times 3[/latex] is less than 15, we put a 3 in the tens place. This represents the 3 longs that were put into each circle. Then we subtract [latex]4\times 3=12[/latex] from 15 to show that we have now used 12 of the 15 longs and have 3 longs remaining. |
 |
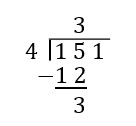 |
| We have three unused longs that cannot be distributed evenly into the 4 circles in their current form, so we need to break them into 30 units, meaning we have 31 total unit pieces. | In long division, we say you "bring down the 1." This represents moving from 3 pieces of size ten to 31 pieces of size one. |
 |
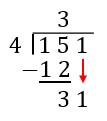 |
| Now we distribute the units as evenly as possible, placing 7 pieces in each circle, using a total of 28 unit pieces. | Because [latex]4\times 8[/latex] is more than 31, and [latex]4\times 7[/latex] is less than 31, we put a 7 in the ones place. This represents the 7 units that were put into each circle. Then we subtract [latex]4\times 7=28[/latex] from 31 to show that we have now used 28 of the 31 unit pieces and have 3 unit pieces leftover. |
 |
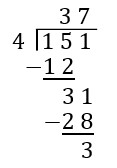 |
| We have 3 units leftover, which is smaller than 4. We are done! Our quotient is what is inside the circle, and our remainder is 3. | We have 3 leftover, which is smaller than 4, so this is our remainder. Our quotient is what is above the line (what is in a circle) with a remainder of 3. |
| Answer: 37 remainder 3 | Answer: 37 remainder 3 |
Exercise 1
Evaluate [latex]794\div 6[/latex] by
a. partitioning into subsets;
b. long division.
Match the numbers in the long division algorithm to your steps with the base ten blocks.
Solution
132 R. 2.
The 1 in the hundreds place represents the 1 flat put into each subset. Then the remaining flat was converted to longs for a total of 19 longs. The 3 in the tens place represents the 3 longs put into each subset. Then the remaining length was converted to units for a total of 14 units. The 2 in the ones place represents the 2 units put into each subset. There were 2 units leftover, giving a remainder of 2.
Exercise 2
Solve the following division problems using long division. Do not use a calculator!
a. [latex]854\div 3[/latex]
b. [latex]36,582\div 3[/latex]
c. [latex]1043\div 11[/latex]
Long Division in Other Number Bases
This same process can be done with different number bases. If you can confidently perform long division calculations in other number bases, you will be better prepared to help your future students understand long division in base ten.
Be aware that your multiplication facts look different in each base. For example, in base ten, [latex]2\times 5=10[/latex], but in base six [latex]2\times 3=10_{\text{six}}[/latex]. Let's consider [latex]345_{\text{six}}\div4_{\text{six}}[/latex] by partitioning with blocks and using long division. Before starting our long division, it is helpful to write out our multiplication facts for 4 in base six. We only need the facts for each digit possible in base six: 0, 1, 2, 3, 4, and 5.
| [latex]4_{\text{six}}\times 0_{\text{six}}[/latex] | = | [latex]0_{\text{six}}[/latex] |
| [latex]4_{\text{six}}\times 1_{\text{six}}[/latex] | = | [latex]4_{\text{six}}[/latex] |
| [latex]4_{\text{six}}\times 2_{\text{six}}[/latex] | = | [latex]12_{\text{six}}[/latex] |
| [latex]4_{\text{six}}\times 3_{\text{six}}[/latex] | = | [latex]20_{\text{six}}[/latex] |
| [latex]4_{\text{six}}\times 4 _{\text{six}}[/latex] | = | [latex]24_{\text{six}}[/latex] |
| [latex]4_{\text{six}}\times 5_{\text{six}}[/latex] | = | [latex]32_{\text{six}}[/latex] |
| Action with Base Six Blocks | Matching Action in Long Division |
 |
|
| First, we need to trade the three flats for [latex]30_{\text{six}}[/latex] (which is 18) longs. This gives a total of [latex]34_{\text{six}}[/latex] (which is twenty-two) longs. | Since "4 cannot go into 3," we look at the number [latex]340_{\text{six}}[/latex] instead of [latex]300_{\text{six}}[/latex]. |
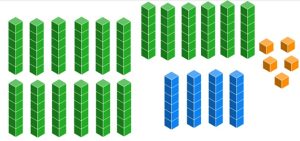 |
|
| Next, we distribute twenty ([latex]32_{\text{six}}[/latex]) of the twenty-two ([latex]34_{\text{six}}[/latex]) longs into the 4 circles by putting five longs in each circle. | Because [latex]4_{\text{six}}\times 5_{\text{six}}[/latex] is close to without going over [latex]34_{\text{six}}[/latex], we put a 5 in the sixes place. This represents the 5 longs that were put into each circle. Then we subtract [latex]4_{\text{six}}\times 5_{\text{six}}=32_{\text{six}}[/latex] from [latex]34_{\text{six}}[/latex] to show that we have now used [latex]32_{\text{six}}[/latex] (which is twenty) of the [latex]34_{\text{six}}[/latex] (which is twenty-two) longs and have 2 longs remaining. |
 |
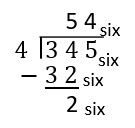 |
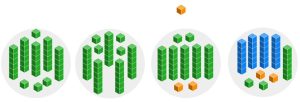
| We have two unused longs that cannot be distributed evenly into the 4 circles in their current form, so we need to break them into twelve ([latex]20 _{\text{six}}[/latex]) units, meaning we have seventeen ([latex]25 _{\text{six}}[/latex]) total unit pieces. | "Bring down the 5" to show that we are converting the 2 in the sixes place to unit pieces, leaving us with [latex]25_{\text{six}}[/latex] unit pieces (i.e., seventeen unit pieces). |
 |
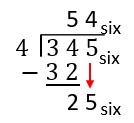 |
| Now we distribute the units as evenly as possible, placing 4 pieces in each circle, using a total of sixteen ([latex]24 _{\text{six}}[/latex]) unit pieces. | Because [latex]4_{\text{six}}\times 5_{\text{six}}[/latex] is more than [latex]25_{\text{six}}[/latex], and [latex]4_{\text{six}}\times 4_{\text{six}}[/latex] is less than [latex]25_{\text{six}}[/latex], we put a 4 in the ones place. This represents the 4 units that were put into each circle. Then we subtract [latex]4_{\text{six}}\times 4_{\text{six}}=24_{\text{six}}[/latex] from [latex]25_{\text{six}}[/latex] to show that we have now used [latex]24_{\text{six}}[/latex] of the [latex]25_{\text{six}}[/latex] unit pieces and have 1 unit piece leftover. |
 |
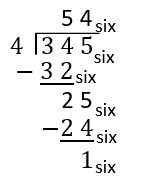 |
| We have 1 unit leftover, which is smaller than 4. We are done! Our quotient is what is inside the circle, and our remainder is 1. | We have 1 leftover, which is smaller than 4, so this is our remainder. Our quotient is what is above the line (what is in a circle) with a remainder of 3. |
| Answer: [latex]54_{\text{six}}[/latex] remainder [latex]1_{\text{six}}[/latex] |
Answer: [latex]54_{\text{six}}[/latex] remainder [latex]1_{\text{six}}[/latex] |
Concept Check: What is wrong in the steps of the following base six long division problem?
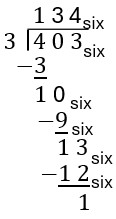
Solution
The division is being done as though everything were in base ten. It is using base ten multiplication facts for 3, instead of base six multiplication facts. For example, 3 does not go into [latex]10_{\text{six}}[/latex] three times. In fact, [latex]3\times 3=13_{\text{six}}[/latex]. The answer should be [latex]121_{\text{six}}[/latex] with no remainder.
There are several ways to figure out the multiples of a number in a given base. One way is to use repeated addition. If you are trying to solve [latex]4301_{\text{five}}\div 13_{\text{five}}[/latex], you need the multiples of [latex]13_{\text{five}}[/latex] up to 4. We know [latex]13_{\text{five}}\times 1_{\text{five}}=13_{\text{five}}[/latex], so we can start there and repeatedly add [latex]13_{\text{five}}[/latex] until we have our first few multiples.
[latex]13_{\text{five}}\times 1_{\text{five}}=\color{blue}13_{\text{five}}[/latex]
[latex]13_{\text{five}}\times 2_{\text{five}}={\color{blue}13_{\text{five}}}+13_{\text{five}}={\color{red}31_{\text{five}}}[/latex]
[latex]13_{\text{five}}\times 3_{\text{five}}={\color{red}31_{\text{five}}}+13_{\text{five}}={\color{cyan}44_{\text{five}}}[/latex]
[latex]13_{\text{five}}\times 4_{\text{five}}={\color{cyan}44_{\text{five}}}+13_{\text{five}}=112_{\text{five}}[/latex]
Exercise 3
a. [latex]1042_{\text{five}}\div 3_{\text{five}}[/latex]
b. [latex]1064_{\text{eight}}\div 7_{\text{eight}}[/latex]
c. [latex]100_{\text{twelve}}\div 7_{\text{twelve}}[/latex]
d. [latex]2202_{\text{three}}\div 12_{\text{three}}[/latex] (Note that [latex]12_{\text{three}}[/latex] is not twelve so you should not have twelve circles.)
Repeated Subtraction Model and Algorithm
Long division is the standard algorithm for division because it keeps work condensed nicely, but it is not the most intuitive algorithm. Repeated subtraction, while more lengthy to write out, feels more intuitive to most people. Again, we will start with blocks and move into numbers.
Exploration Activity
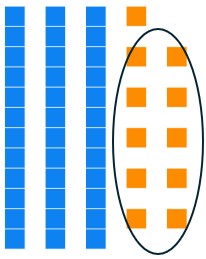
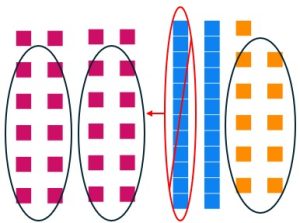
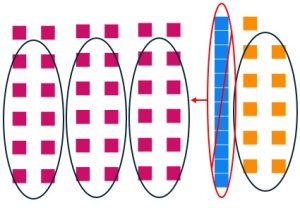
Pull out your base ten blocks. We will solve the base ten division problem [latex]86\div 12[/latex] using repeated subtraction.
a. Lay out 86 in your base ten blocks.
b. We need to make groups of size 12. Separate out as many groups of size 12 as you can without trading any blocks.
c. Trade one long for 10 units and continue making groups of size 12. (You should have 2 unit pieces leftover.)
We know that the answer when using repeated subtraction is the number of subsets/groups made. There are 7 subsets of size 12, and there are 2 units that were not put into any subset. The answer is 7 remainder 2.
As with partitioning into subsets, it is not practical to use blocks for larger numbers, so we need to develop an algorithm that matches the blocks.
| Action with Base Ten Blocks | Matching Action with the Repeated Subtraction Algorithm | |
| We need to make groups of size 12, which is one long and two units each. We can separate out three groups of this size.
|
Begin subtracting 12 repeatedly. We can subtract 12 three times before we do not have enough ones to continue subtracting in the current form. Notice, we are able to subtract 12 three times, matching the three groups we were able to make with the blocks. | 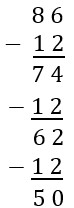 |
| In order to continue making groups of size 12, we need more unit pieces, so break one long into 10 unit pieces, leaving 4 longs and 10 units.
|
Take one from the tens place and convert it to ones, leaving 4 tens and 10 ones. This matches converting one long into unit pieces. | 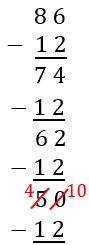 |
| Now we can make 4 more groups of size 12 and that will leave 2 unit pieces left unused.
|
Continue to subtract 12 repeatedly. We can subtract 12 four more times before we have too few pieces to subtract any more. Each "minus 12" matches with creating another group with the blocks. | 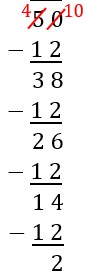 |
| In total, we have created 7 groups/subsets of size 12 and have 2 unit pieces leftover. | Total, we have subtracted 12 seven times and have 2 leftover after all of the subtractions. | |
| Answer: [latex]7[/latex] remainder [latex]2[/latex] | Answer: [latex]7[/latex] remainder [latex]2[/latex] |
Caution: Do not write your repeated subtraction as
[latex]86-12=74-12=62-12=50-12=38-12=26-12=14-12=2.[/latex]
While the calculations are correct, this is an incorrect use of the equals sign. This statement says [latex]74=64=50=38=26=14=2=2[/latex], which is false. Always remember that the equals sign means the two sides are identical in value. It does not mean "next step" or "answer." Proper use of the equals sign in early grades leads to less confusion when students reach algebra.
Exercise 4
Evaluate [latex]67\div 15[/latex] by
a. repeated subtraction with blocks;
b. repeated subtraction with numbers (algorithm).
Match the numbers in your algorithm to your steps with the base ten blocks.
Solution
4 R. 7.
With blocks, one group of size 15 can be made without exchanging any blocks. With numbers, one 15 can be subtracted without needing to trade. But, to make the second group of size 15, we need to exchange one long for ten units. This matches the trading in repeated subtraction, rewriting 52 to be 4 and 12. The next group of 15 can be made without any exchanging/trading. In order the make the last group of size 15, one long needs to be exchanged for ten units, converting 22 into 1 and 12. There are 7 unit pieces leftover.
Exercise 5
Use the repeated subtraction algorithm to evaluate the following division expressions. Do not use a calculator!
a. [latex]103\div 21[/latex]
b. [latex]45\div 9[/latex]
c. [latex]73\div 8[/latex]
Repeated Subtraction in Other Number Bases
As with long division, this same process can be done with other number bases. Pay close attention when subtracting to be sure you do not use base ten values! For example, [latex]10-9=1[/latex] in base ten, but [latex]10_{\text{twelve}}-9_{\text{twelve}}=3_{\text{twelve}}[/latex]. Let's consider [latex]3\text{E}_{\text{twelve}}\div \text{T}_{\text{twelve}}[/latex]. (Recall that "E" is the symbol for eleven and "T" is the symbol for ten.) Since we will be subtracting [latex]\text{T}_{\text{twelve}}[/latex], it will be useful to list our addition facts for [latex]\text{T}_{\text{twelve}}[/latex]. We need all of the digits possible in base twelve: 0, 1, 2, 4, 5, 6, 7, 8, 9, T, and E. Remember that [latex]10_{\text{twelve}}[/latex] is equivalent to the base ten number, twelve.
| [latex]\text{T}_{\text{twelve}}+0[/latex] | = | [latex]\text{T}_{\text{twelve}}[/latex] | [latex]\text{T}_{\text{twelve}}+6[/latex] | = | [latex]14_{\text{twelve}}[/latex] |
| [latex]\text{T}_{\text{twelve}}+1[/latex] | = | [latex]\text{E}_{\text{twelve}}[/latex] | [latex]\text{T}_{\text{twelve}}+7[/latex] | = | [latex]15_{\text{twelve}}[/latex] |
| [latex]\text{T}_{\text{twelve}}+2[/latex] | = | [latex]10_{\text{twelve}}[/latex] | [latex]\text{T}_{\text{twelve}}+8[/latex] | = | [latex]16_{\text{twelve}}[/latex] |
| [latex]\text{T}_{\text{twelve}}+3[/latex] | = | [latex]11_{\text{twelve}}[/latex] | [latex]\text{T}_{\text{twelve}}+9[/latex] | = | [latex]17_{\text{twelve}}[/latex] |
| [latex]\text{T}_{\text{twelve}}+4[/latex] | = | [latex]12_{\text{twelve}}[/latex] | [latex]\text{T}_{\text{twelve}}+\text{T}[/latex] | = | [latex]18_{\text{twelve}}[/latex] |
| [latex]\text{T}_{\text{twelve}}+5[/latex] | = | [latex]13_{\text{twelve}}[/latex] | [latex]\text{T}_{\text{twelve}}+\text{E}[/latex] | = | [latex]19_{\text{twelve}}[/latex] |
| Action with Base Twelve Blocks | Matching Action with the Repeated Subtraction Algorithm |
| Laying out [latex]3\text{E}_{\text{twelve}}[/latex], we see that we have three longs and eleven units. We need to make groups of size [latex]\text{T}_{\text{twelve}}[/latex], which is ten units. We can create one group without trading any blocks. This leaves three longs and one unit to still be grouped.
|
We can subtract [latex]\text{T}_{\text{twelve}}[/latex] once before we do not have enough ones to continue subtracting in the current form. "Eleven minus ten" is one, so [latex]\text{E}_{\text{twelve}}-\text{T}_{\text{twelve}}=1[/latex]. Notice, this matches the one group we were able to make with the blocks and the one unit we have leftover.
|
| To continue making groups of size [latex]\text{T}_{\text{twelve}}[/latex], we need more unit pieces, so exchange one long into twelve unit pieces, leaving two longs and thirteen units. Create one more group of size [latex]\text{T}_{\text{twelve}}[/latex], which leaves two longs and three units.
|
Take one from the twelves place and convert it to ones, leaving 2 twelves, and 11_{\text{twelve}} ones (i.e, thirteen ones). This matches converting one long into unit pieces. We need to evaluate [latex]11_{\text{twelve}}-\text{T}_{\text{twelve}}[/latex]. According to our addition facts, [latex]\text{T}_{\text{twelve}}+3= 11_{\text{twelve}}[/latex], so [latex]11_{\text{twelve}}-\text{T}_{\text{twelve}}=3.[/latex] This gives the answer of [latex]23_{\text{twelve}}[/latex], matching our two longs and three units remaining.
|
| Now we must trade another long for more unit pieces, leaving one long and fifteen units. Creating another group of size [latex]\text{T}_{\text{twelve}}[/latex] leaves one long and five units.
|
Take one from the twelves place and convert it to ones, leaving 1 twelves, and 13_{\text{twelve}} ones (i.e, fifteen ones). This matches converting one long into unit pieces. We need to evaluate [latex]13_{\text{twelve}}-\text{T}_{\text{twelve}}[/latex]. According to our addition facts, [latex]\text{T}_{\text{twelve}}+5= 13_{\text{twelve}}[/latex], so [latex]13_{\text{twelve}}-\text{T}_{\text{twelve}}=5.[/latex] This gives the answer of [latex]15_{\text{twelve}}[/latex], matching our one long and five units remaining.
|
| Again, we must trade a long for more unit pieces. Trading our last long gives us seventeen units. We can create one more group of size [latex]\text{T}_{\text{twelve}}[/latex] and have seven units leftover.
|
We now have [latex]15_{\text{twelve}}-\text{T}_{\text{twelve}}[/latex]. According to our addition facts, [latex]\text{T}_{\text{twelve}}+7= 15_{\text{twelve}}[/latex], so [latex]15_{\text{twelve}}-\text{T}_{\text{twelve}}=7.[/latex] This gives the answer of [latex]7_{\text{twelve}}[/latex], matching seven units remaining.
|
| In total, we have created 4 groups/subsets of size [latex]\text{T}_{\text{twelve}}[/latex] and have 7 unit pieces leftover. | Total, we have subtracted [latex]\text{T}_{\text{twelve}}[/latex] four times and have 7 leftover after all of the subtractions. |
| Answer: [latex]4_{\text{twelve}}[/latex] remainder [latex]7_{\text{twelve}}[/latex] | Answer: [latex]4_{\text{twelve}}[/latex] remainder [latex]7_{\text{twelve}}[/latex] |
Concept Check: Look over the work below, solving [latex]210_{\text{three}}\div 11_{\text{three}}[/latex]. The calculation was performed correctly, but there is something wrong with the answer. What is it?
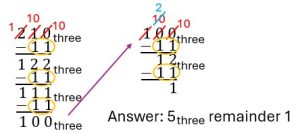
Solution
The symbol 5 does not exist in base three. It is true that [latex]11_{\text{three}}[/latex] was subtracted five times, but we must represent the number five in base three's language. The answer should be [latex]12_{\text{three}}[/latex] with remainder 1.
Before beginning a repeated subtraction problem in an unusual number base, it is useful to list out your addition facts for all digits appearing in the divisor. For example, for the problem [latex]244_{\text{five}} \div 32_{\text{five}}[/latex] you would need the addition facts for both the digits 2 and 3.
| [latex]2+1=3_{\text{five}}[/latex] | [latex]3+1=4_{\text{five}}[/latex] |
| [latex]2+2=4_{\text{five}}[/latex] | [latex]3+2=10_{\text{five}}[/latex] |
| [latex]2+3=10_{\text{five}}[/latex] | [latex]3+3=11_{\text{five}}[/latex] |
| [latex]2+4=11_{\text{five}}[/latex] | [latex]3+4=12_{\text{five}}[/latex] |
Exercise 6
(Fast) Repeated Subtraction
For the problems above, repeated subtraction wasn't too tedious, but when facing a division problem like [latex]4025\div 3[/latex], it is not practical to repeatedly subtract 3. It would take over 1,000 steps to finish the algorithm! Thus, we must alter our repeated subtraction algorithm a little bit in order to make the process a feasible number of steps. The key idea is to subtract multiple groups of size 3 at one time instead of individually. We will accomplish this by using easy multiples of 3.
| Thought Process | Written Work (Scaffold) |
| 4023 is larger than 3000, which is 1000 groups of size 3. So if we subtract 3000, we are measuring out 1000 groups in one step. This leaves 1025 leftover. In our work, we show the number of pieces on the left and the number of groups on the right. | 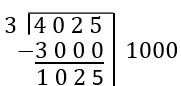 |
| Now we need to find a multiple of 3 close to 1025. We can use any multiple, so let's use 900. This is 300 groups of 3. Subtracting 900 from 1025 leaves 125. We have now made 1300 groups of size 3. | 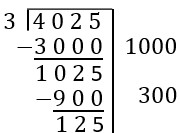 |
| Continue the process of finding multiples of 3 close to our leftover number. the number 120 is 40[latex]\times[/latex]3, which is close to 125. Subtracting 125 from 120 leaves 5. We have made 1340 groups of size 3. | 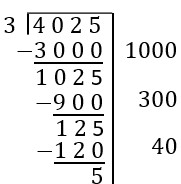 |
| Finally, we can subtract one more group of size 3, to see we have a remainder of 2. The right-hand side of our work shows the total number of groups of size 3 we used.
Totaling up the number of groups created, we have [latex]1000+300+40+1=1341[/latex] groups of size 3.
Answer: [latex]1341[/latex] remainder [latex]2[/latex] |
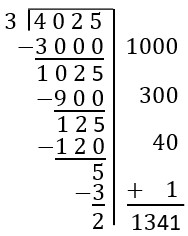 |
Exercise 7
Classroom Connection: You have your students solve [latex]3854\div 3[/latex] using repeated subtraction and compare their work with a partner. One pair of students is confused because their work is so different, but they both got the same answer. (Shown below.) The students want to know whose way is better. What do you tell them?

Solution
Both students are correct. The first student chose to use multiples of 3 based on powers of ten. The second student chose to use multiples of 3 based on doubles (powers of two). In the end, both of them found 1284 groups of size 3 with 2 leftover. The work on the left was easier to add because it was multiples of ten. The work on the right took fewer steps. Neither way is "better." As long as you efficiently subtract multiples of 3, it does not matter which multiples of 3 you use.
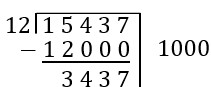
Reconsider exercise 7, part b. You may have had a difficult time choosing efficient powers of ten that worked. Using doubles can sometimes make the problem much more efficient. To use doubles, take your divisor, double it, then double that answer, and keep repeating the process until you have a large number close to your desired number. Suppose you start the problem by subtracting 12,000. Now, if you cannot think of a nice multiple of 12 close to 3,437, you can list out doubles to see if any of them are close.
| Doubling | Multiplication represented |
| [latex]12+12=24[/latex] | [latex]12\times 2[/latex] |
| [latex]24+24=48[/latex] | [latex]12\times 4[/latex] |
| [latex]48+48=96[/latex] | [latex]12\times 8[/latex] |
| [latex]96+96=192[/latex] | [latex]12\times 16[/latex] |
| [latex]192+192=384[/latex] | [latex]12\times 32[/latex] |
| [latex]384+384=768[/latex] | [latex]12\times 64[/latex] |
| [latex]768+768=1536[/latex] | [latex]12\times 128[/latex] |
| [latex]1536+1536=3072[/latex] | [latex]12\times 256[/latex] |
| [latex]3072+3072=6144[/latex] | [latex]12\times 512[/latex] |
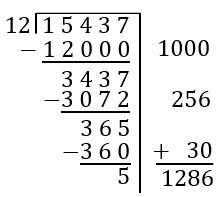
Notice that [latex]12\times 256=3072[/latex] is close to the desired 3,437, so we can use that in our scaffold and continue. This is probably fewer steps than you used when solving Exercise 7, part b. In different situations, different approaches will be more efficient. Some people see doubles very easily, and some do not. As a teacher, you will need to keep yourself open to the variety of approaches students might take.
Exercise 8
Evaluate [latex]1800\div 7[/latex] using (fast) repeated subtraction and doubles.
Solution
Starting with 7 and writing out doubles, the closest we get to 1800 is [latex]7\times 256=1792[/latex]. Subtracting [latex]1800-1792=8[/latex]. We can get one more 7 out of 8, so the answer is 257 with a remainder of 1.
The moral of the story is that you can use any multiples you are comfortable using. The closer you can get to the total, the fewer steps you will have.
(Fast) Repeated Subtraction in Other Number Bases
As with our other algorithms, we should extend smart repeated subtraction to other number bases. Consider [latex]4324_{\text{five}}\div 4_{\text{five}}[/latex]. Since we do not have them memorized, we should write out our multiplication facts for 4 to make it easier.
| [latex]4\times 1=4_{\text{five}}\;\;[/latex] |
| [latex]4\times 2=13_{\text{five}}[/latex] |
| [latex]4\times 3=22_{\text{five}}[/latex] |
| [latex]4\times 4=31_{\text{five}}[/latex] |
| Thought Process | Written Work (Scaffold) |
| Note that [latex]4000_{\text{five}}=4\times 1000_{\text{five}}[/latex] is close to [latex]4324_{\text{five}}[/latex]. We can subtract [latex]4000_{\text{five}}[/latex] from [latex]4324_{\text{five}}[/latex] to get [latex]1000_{\text{five}}[/latex] groups of size 4 with [latex]324_{\text{five}}[/latex] unused so far. | 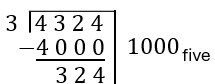 |
| Now we need to find a multiple of 4 close to [latex]324_{\text{five}}[/latex]. Notice that [latex]4\times 4=31_{\text{five}}[/latex], so that means [latex]4\times 40_{\text{five}}=310_{\text{five}}[/latex]. Subtracting [latex]310_{\text{five}}[/latex] from [latex]324_{\text{five}}[/latex] leaves [latex]14_{\text{five}}[/latex]. Since [latex]310_{\text{five}}[/latex] was [latex]40_{\text{five}}[/latex] groups of size 4, we have now made [latex]1040_{\text{five}}[/latex] groups of size 4. |  |
| The closest multiple of 4 to [latex]14_{\text{five}}[/latex] is [latex]4\times 2=13_{\text{five}}[/latex]. Thus, we can subtract two more groups of size 4. Solving [latex]14_{\text{five}}-13_{\text{five}}[/latex] yields a remainder of 1.
Totaling up the number of groups created, we have [latex]1000_{\text{five}}+40_{\text{five}}+2_{\text{five}}=1042_{\text{five}}[/latex] groups of size 4 with 1 leftover.
Answer: [latex]1042_{\text{five}}[/latex] remainder [latex]1_{\text{five}}[/latex] |
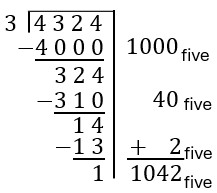 |
Exercise 9
a. [latex]1042_{\text{five}}\div 3_{\text{five}}[/latex]
b. [latex]1064_{\text{eight}}\div 7_{\text{eight}}[/latex]
c. [latex]100_{\text{twelve}}\div 7_{\text{twelve}}[/latex]
d. [latex]2202_{\text{three}}\div 12_{\text{three}}[/latex] (Note that [latex]12_{\text{three}}[/latex] is not twelve, so you should not have twelve circles.)