41 Multiplication and Division of Fractions
Louisiana Student Standards
Standard Number |
Description of Standard |
| 4.NF.B.4. | Multiply a fraction by a whole number. (Denominators are limited to[latex]2, 3, 4, 5, 6, 8, 10, 12,[/latex] and [latex]100[/latex].) |
| 5.NF.B.4. | Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction. |
| 5.NF.B.7. | Apply and extend previous understandings of division to divide unit fractions by whole numbers and whole numbers by unit fractions. |
| 6.NS.A. | Apply and extend previous understandings of multiplication and division to divide fractions by fractions. |
You will need:
Exploration Activity
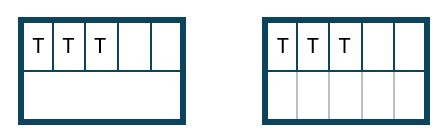
You are sharing a rectangular garden with your best friend. You each get half of the garden.
-
- Make a diagram of the garden showing your half and your friend’s half.
- You are going to plant tomatoes in [latex]\frac{3}{5}[/latex] of your half. Add this to your diagram.
- Your friend is only going to plant flowers. Consider your diagram. What fraction of the whole garden will be tomatoes?
Solution
[latex]\frac{3}{10}[/latex] will be tomatoes. If it takes five pieces to make up half of the garden, it will take ten pieces to make up the whole garden. But, only 3 of those pieces are tomatoes.
In the Exploration Activity you visualized [latex]\frac{1}{2}\times\frac{3}{5}[/latex] using the rectangle model of multiplication. In general, there are three ways to visualize multiplication with fractions: the dot model, the repeated addition model, or the rectangle model of multiplication.
Multiplying a Fraction and a Whole Number
If one of our two numbers is a whole number, we can use the dot model for fractions or the repeated addition approach to multiplication.
You actually multiplied fractions in the first section of this module Concept of Fraction when you used the dot model, so let’s revisit this idea first.
Example 1
Solve [latex]36\times\frac{4}{9}[/latex] using the dot model.
Solution
First, we need to make sure we understand what the problem is asking. The product [latex]36\times\frac{4}{9}[/latex] represents four-ninths of 36. Thus, we are being asked to find [latex]\frac{4}{9}[/latex] of 36. In other words,
[latex]\displaystyle\frac{4}{9}=\frac{?}{36}[/latex].
Drawing out 36 dots and dividing them into ninths gives 4 dots per group.

Since we want four-ninths, we need to consider four of the groups.
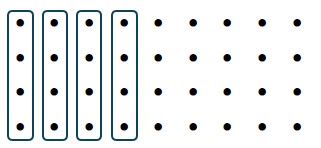
These four groups contain 16 dots total between them. Thus [latex]\frac{4}{9}=\frac{16}{36}[/latex]. In other words,
[latex]\displaystyle 36\times\frac{4}{9}=16[/latex].
The dot model only works if we can evenly partition our whole number into the proper amount of equal groups. You would not want to use the dot model for something like [latex]5\times\frac{4}{11}[/latex] because you cannot evenly divide 5 dots into elevenths. In this case, the better approach is to use repeated addition.
Example 2
Solve [latex]5\times\frac{4}{11}[/latex] using repeated addition.
Solution
Repeated addition tells us we need to add [latex]\frac{4}{11}[/latex] five times. In terms of our fraction tiles, it would look like five groups of size [latex]\frac{4}{11}[/latex].
From the fraction tiles we can see that we have 20 pieces of size one-eleventh, making our answer [latex]\frac{20}{11}[/latex]. When converting the visual of our fraction tiles to numbers, we have
[latex]\displaystyle \frac{4}{11}+\frac{4}{11}+\frac{4}{11}+\frac{4}{11}+\frac{4}{11}[/latex].
Since all of our fractions have a common denominator, we can add the numerators.
[latex]\displaystyle \frac{4+4+4+4+4}{11}=\frac{20}{11}[/latex].
Students typically start with logic similar to the dot model because it matches our concept of what a fraction is. The repeated addition model requires students to understand the repeated addition model of multiplication and know how to add fractions.
Exercise 1
For each of the following products determine if it can be represented with the dot model. If it can, show the dot model.
- [latex]45\times\frac{2}{9}[/latex]
- [latex]45\times\frac{2}{7}[/latex]
- [latex]35\times\frac{5}{9}[/latex]
- [latex]35\times\frac{5}{7}[/latex]
Solution
a and d can be represented with the dot model because the denominator is a factor of the whole number.
Solution to (a)
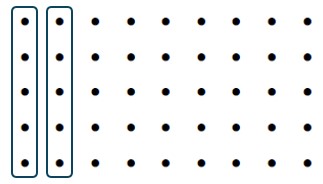
Solution to (d)
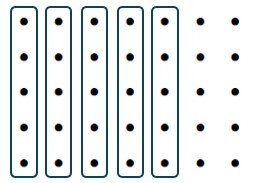
b and c cannot be represented with the dot model because the denominator is not a factor of the whole number.
Exercise 2
Solve the following multiplication problems using repeated addition.
- [latex]6\times\frac{8}{11}[/latex]
Solution
[latex]\frac{8}{11}+\frac{8}{11}+\frac{8}{11}+\frac{8}{11}+\frac{8}{11}+\frac{8}{11}=\frac{6\times 8}{11}=\frac{48}{11}[/latex] or [latex]4\;\frac{4}{11}[/latex]
- [latex]3\times\frac{7}{9}[/latex]
Solution
[latex]\frac{7}{9}+\frac{7}{9}+\frac{7}{9}=\frac{3\times 7}{9}=\frac{21}{9}=\frac{7}{3}[/latex] or [latex]2\;\frac{1}{3}[/latex]
- [latex]4\times\frac{2}{5}[/latex]
Solution
[latex]\frac{2}{5}+\frac{2}{5}+\frac{2}{5}+\frac{2}{5}=\frac{4\times 2}{5}=\frac{8}{5}[/latex] or [latex]1\;\frac{3}{5}[/latex]
- [latex]5\times\frac{7}{10}[/latex]
Solution
[latex]\frac{7}{10}+\frac{7}{10}+\frac{7}{10}+\frac{7}{10}+\frac{7}{10}=\frac{5\times 7}{10}=\frac{35}{10}=\frac{7}{2}[/latex] or [latex]3\;\frac{1}{2}[/latex]
Concept Check:
- Why is it important that one of our numbers be a whole number in order to use repeated addition or the dot model?
Solution
For the dot model, you need a whole number to know how many dots to draw. If you are trying to multiply [latex]\frac{1}{2}\times\frac{3}{4}[/latex] it doesn’t make sense to draw dots.
For repeated addition, you need a whole number to tell you how many times to repeat the fraction.
- Will you ever need to change the fractions to have a common denominator with the repeated addition model?
Solution
No. Since you are using the same fraction over and over, the denominators already match.
Multiplying two Fractions
If we do not have a whole number, we need another way to visualize multiplication of fractions. The easiest way is to use rectangles. Recall that [latex]5\times 8[/latex] can be represented by the area of a 5 by 8 rectangle.
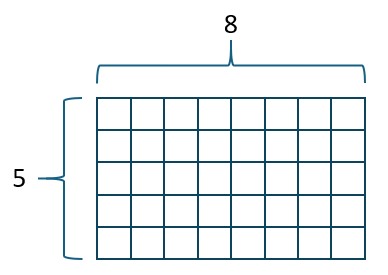
We can use the same concept for fractions. We simply need to keep track of what makes a unit so that we can interpret our answer.
Let’s revisit our situation from the Exploration Activity, [latex]\frac{1}{2}\times\frac{3}{5}[/latex]. Our unit is the entire garden.
First we split that unit into halves. Since we want one-half, shade one of the two halves.

Next we consider the unit split into fifths. Since we did the halves horizontally, we make the fifths vertical. Since we want three-fifths, shade three of the five fifths.
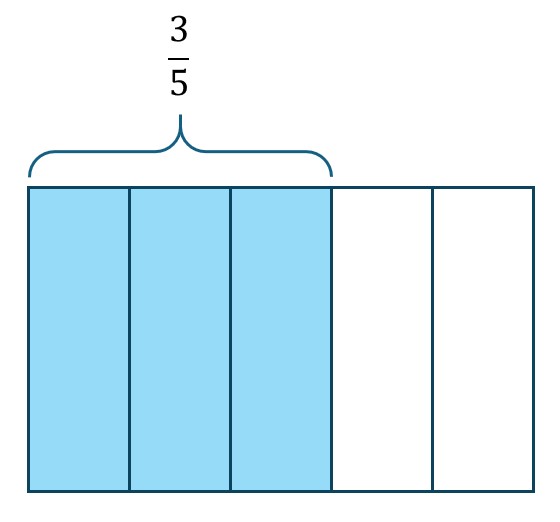
If we lay the two fractions on top of each other, their product is the overlap of the two shaded areas.
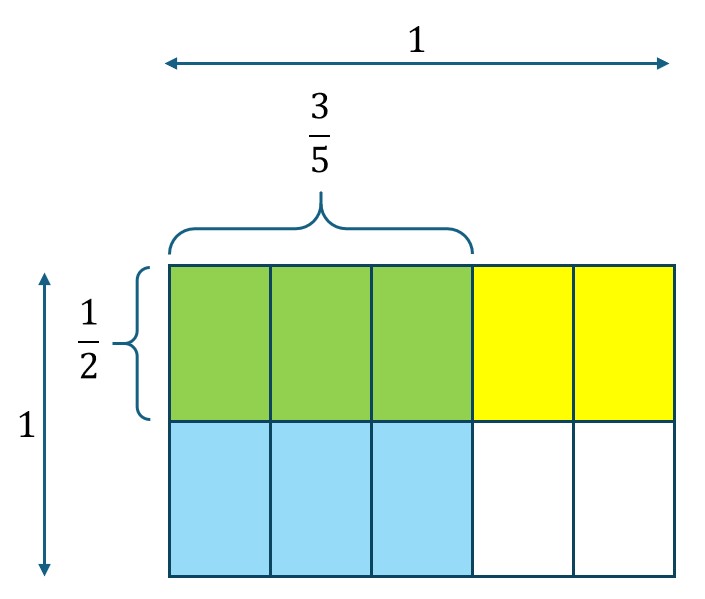
Our overlap is three pieces and the unit now consists of ten pieces. Thus our answer is [latex]\frac{3}{10}[/latex].
When you solved the exploration activity, your picture probably looked something like the following.
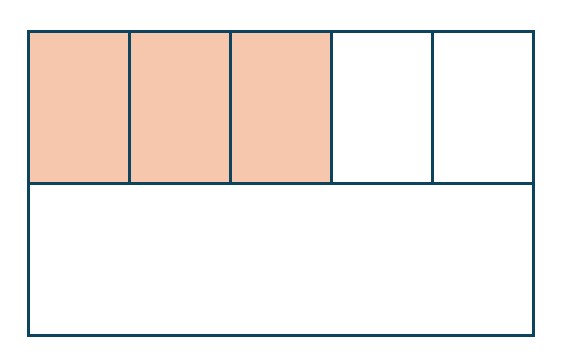
Does this look familiar to our overlap picture? When you multiply two fractions you are dividing each dimension of the rectangle into each fraction. It just helps to draw the lines all the way through so that we can determine our denominator.
Exercise 3
Evaluate the following products using the rectangle model.
- [latex]\displaystyle \frac{3}{5}\times\frac{1}{6}[/latex]
Solution

Answer: [latex]\displaystyle \frac{3}{30}[/latex] or [latex]\displaystyle \frac{1}{10}[/latex]
- [latex]\displaystyle \frac{2}{7}\times\frac{2}{9}[/latex]
Solution
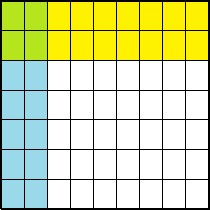
Answer: [latex]\displaystyle \frac{4}{63}[/latex]
- [latex]\displaystyle \frac{1}{3}\times\frac{3}{8}[/latex]
Solution
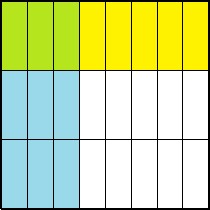
Answer: [latex]\displaystyle \frac{3}{24}[/latex] or [latex]\displaystyle \frac{1}{8}[/latex]
- [latex]\displaystyle \frac{3}{4}\times\frac{1}{4}[/latex]
Solution

Answer: [latex]\displaystyle \frac{3}{16}[/latex]
Algorithm for Multiplying Fractions
Models work well to visualize what is happening with smaller numbers, but they are not reasonable for products like [latex]\frac{56}{101}\times\frac{7}{43}[/latex]. The “multiply across” algorithm is an approach that works for all fraction combinations. This algorithm was covered in the Pre Unit Review Multiply and Divide Fractions. But now you have a stronger understanding of what multiplication of fractions looks like, so let’s review this algorithm.
Reconsider the rectangles you drew in Exercise 3. The number of pieces in the overlap was always the product of the numerators and the number of pieces in the entire rectangle was always the product of the denominators. That is exactly what our algorithm says!
Algorithm to Multiply Fractions
Let a, b, c, and d be numbers where b and d are not zero. Then
[latex]\displaystyle \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}[/latex].
Exercise 4
Solve [latex]\frac{4}{5}\times\frac{2}{3}[/latex] both by using the rectangle model and by using the algorithm. Explain how each piece in the picture of the rectangle relates to each piece in the algorithm.
Solution
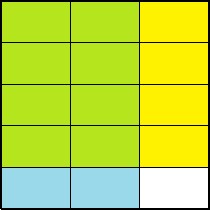
[latex]\displaystyle\frac{4}{5}\times\frac{2}{3}=\frac{4\times 2}{5\times 3}=\frac{8}{15}[/latex]
Where the shaded areas overlap is a 4 by 2 rectangle. This matches with the numerator in our algorithm. The overall unit rectangle is split into [latex]5\times 3[/latex] pieces. This matches with the denominator in our algorithm.
Notice that we don’t need a common denominator to multiply fractions. This is a big difference between multiplication and addition. When adding, we need like things: inches plus inches, minutes plus minutes, etc. We cannot add inches plus minutes. But, we can multiply different denominators. For example, 4 inches/minute times 5 minutes is a reasonable product. It equals 20 inches. So, we multiply two different units and end up with a third type of unit. Multiplication of fractions is similar; we can start with two different kinds of fractions and multiply to get a third.
When multiplying mixed numbers you can either use the distributive property or convert the mixed number to an improper fraction. Let’s consider [latex]\frac{2}{3}\times3\;\frac{4}{5}[/latex].
Option 1: Distributive Property
[latex]\begin{align*}\displaystyle\frac{2}{3}\times 3\;\frac{4}{5}&=\frac{2}{3}\left(3+\frac{4}{5}\right)\\&=\frac{2}{3}\times 3 +\frac{2}{3}\times\frac{4}{5}\\ &=2+\frac{8}{15}\\&=2\;\frac{8}{15}\end{align*}[/latex]
Option 2: Convert to Improper Fraction
[latex]\displaystyle\frac{2}{3}\times3\;\frac{4}{5}=\frac{2}{3}\times\frac{19}{5}=\frac{38}{15}[/latex]
Most people prefer the improper fraction method, but if you do not have a calculator handy, using the distributive property will keep the numbers smaller.
Exercise 5
For each of the following, evaluate the product by either using the distributive property or by converting to improper fractions. You may give your answer as a mixed number or an improper fraction, but be sure to simplify your answer.
a. [latex]4\;\frac{1}{3}\times\frac{3}{8}[/latex]
Solution
Improper Fractions Method:
[latex]\frac{13}{3}\times\frac{3}{8}=\frac{39}{24}=\frac{13}{8}[/latex]
Distributive Property Method:
[latex]\left(4\times\frac{3}{8}\right)+\left(\frac{1}{3}\times\frac{3}{8}\right)=\frac{12}{8}+\frac{1}{8}=\frac{13}{8}[/latex]
b. [latex]6\;\frac{4}{5}\times\frac{1}{10}[/latex]
Solution
Improper Fractions Method:
[latex]\frac{34}{5}\times\frac{1}{10}=\frac{34}{50}=\frac{17}{25}[/latex]
Distributive Property Method:
[latex]\left(6\times\frac{1}{10}\right)+\left(\frac{4}{5}\times\frac{1}{10}\right)=\frac{3}{5}+\frac{2}{25}=\frac{15}{25}+\frac{2}{25}=\frac{17}{25}[/latex]
c. [latex]1\;\frac{5}{12}\times\frac{11}{12}[/latex]
Solution
Improper Fractions Method:
[latex]\frac{17}{12}\times\frac{11}{12}=\frac{187}{144}[/latex]
Distributive Property Method:
[latex]\left(1\times\frac{11}{12}\right)+\left(\frac{5}{12}\times\frac{11}{12}\right)=\frac{11}{12}+\frac{55}{144}=\frac{132}{144}+\frac{55}{144}=\frac{187}{144}[/latex]
d. [latex]2\;\frac{2}{7}\times 3\;\frac{1}{2}[/latex]
Solution
Improper Fractions Method:
[latex]\frac{16}{7}\times\frac{7}{2}=\frac{112}{14}=8[/latex]
Distributive Property Method:
[latex]\left(2\times 3\right)+\left(2\times\frac{1}{2}\right)+\left(\frac{2}{7}\times 3\right)+\left(\frac{2}{7}\times\frac{1}{2}\right)=6+1+\frac{6}{7}+\frac{1}{7}=8[/latex]
Classroom Connection: Your students have been practicing how to multiply mixed numbers and Grace wants to know if there is a way to use the rectangle model to represent the product of mixed numbers. What do you think?
Solution
Yes you can! You just have to be careful about keeping track of how many pieces make up a unit. Let’s look at [latex]\frac{7}{10}\times1\;\frac{2}{3}[/latex].
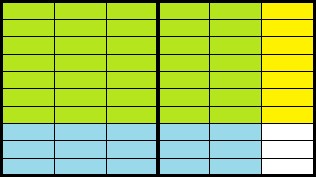
Our picture shows two units, each made up of 30 pieces. The overlap between the shaded areas is 35 pieces. Thus, our answer is [latex]\frac{35}{30}[/latex] which simplifies to [latex]\frac{7}{6}[/latex] or [latex]1\;\frac{1}{6}[/latex].
Applications of Fraction Multiplication
Now that you can visualize a product of fractions, use that skill in the following word problems. For each one, draw a picture using one of our models for fractions. You may check your answer using the “multiply across” algorithm.
Exercise 6
Solve the following word problems using a visual model.
- A baseball shop has 60 baseball gloves. If [latex]\frac{1}{5}[/latex] of the gloves are left-handed gloves, how many left-handed gloves does the shop have?
Solution

[latex]\displaystyle 60\times\frac{1}{5}=12[/latex]
The shop has 12 baseball gloves.
- Your cat eats [latex]\frac{3}{4}[/latex] of a cup of food each day. How much food will your cat eat in a week?
Solution
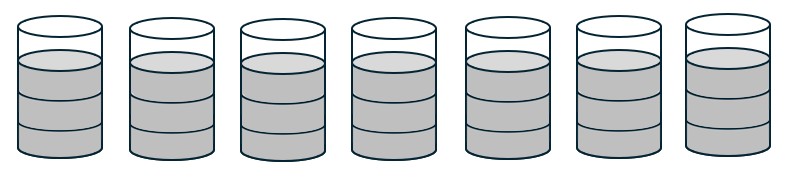
[latex]\displaystyle\frac{3}{4}+\frac{3}{4}+\frac{3}{4}+\frac{3}{4}+\frac{3}{4}+\frac{3}{4}+\frac{3}{4}=\frac{21}{4}[/latex]
The cat eats [latex]5\;\frac{1}{4}[/latex] cups a week.
- A toy company is designing a new playhouse. In the playhouse everything is [latex]\frac{3}{5}[/latex] the size it would be in a regular house. If a notepad is [latex]\frac{7}{12}[/latex] of a foot long in a regular house, how long will a notepad be in the playhouse?
Solution
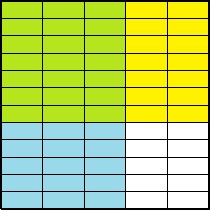
The notepad will be [latex]\frac{21}{60}=\frac{7}{20}[/latex] feet long.
Exploration Activity
Imagine you have to do your laundry at an old fashioned laundromat where you have to pay with quarters. You need to go to the bank and get some quarters.
a. If you convert 10 dollars into quarters, how many quarters will you have?
b. Represent [latex]10\div 2[/latex] on the number-line using the repeated subtraction model of division.
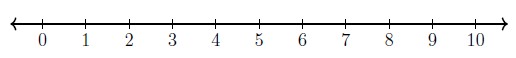
Solution

Five groups of size 2, so [latex]10\div 2=5[/latex].
c. Similar to what you did in part (b), represent [latex]10\div\frac{1}{4}[/latex] on the number-line using the repeated subtraction model of division.
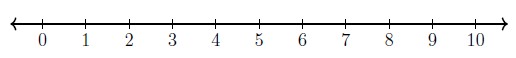
Solution
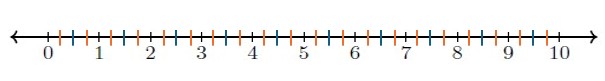
Forty groups of size [latex]\displaystyle\frac{1}{4}[/latex], so [latex]10\div\frac{1}{4}=40[/latex].
d. A quarter is [latex]\frac{1}{4}[/latex] of a dollar. Explain how your process in part (a) relates to your process in part (c).
Solution
For the number line (repeated subtraction), we split each whole into 4 pieces to get pieces of size one-fourth. This gave us forty pieces of size one-fourth. With the money example, we split each dollar into 4 pieces of size one-fourth (aka a quarter). This gave use forty quarters because each has size one-fourth.
Dividing by fractions can feel counterintuitive. Recall the classroom scenario from the beginning of Understanding Division. The students were confused about the difference between dividing BY half and dividing IN half. Let’s use our two models of division, partitioning into equal subsets and repeated subtraction, to visualize what is going on when we divide by a fraction.
Fraction Division by Partitioning into Equal Subsets
If we have a fraction divided by a whole number, we can use the partitioning into equal subsets model of division. The steps are the same as with whole numbers:
- start with the first number
- divide that number up into equal subsets.
Your answer will be how many things are in one subset. The only difference from whole numbers is we need to keep track of how many pieces make up a unit in order to determine our denominator.
Example 3
Solve [latex]\frac{8}{11}\div 5[/latex] using partitioning into equal subsets.
Solution
First we need to represent [latex]\frac{8}{11}[/latex] using the rectangle model.

Next, we need to divide that representation into 5 equal subsets.
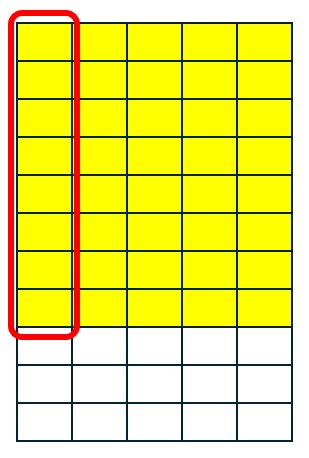
Our answer is the pieces contained in one subset. According to our picture, each subset contains 8 pieces. Because our unit consists of 55 pieces, each of those pieces has size [latex]\frac{1}{55}[/latex].
Answer:[latex]\displaystyle\frac{8}{55}[/latex]
Exercise 7
Solve the following problems by partitioning into equal subsets.
- [latex]\frac{3}{5}\div 6[/latex]
Solution
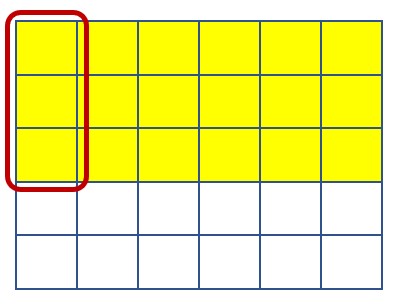
Answer:[latex]\frac{3}{30}[/latex] or [latex]\frac{1}{10}[/latex]
- [latex]\frac{2}{9}\div 5[/latex]
Solution
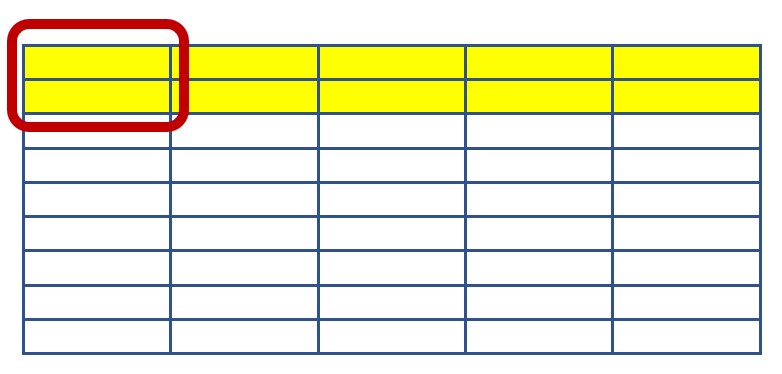
Answer:[latex]\frac{2}{45}[/latex]
- [latex]\frac{3}{2}\div 8[/latex]
Solution
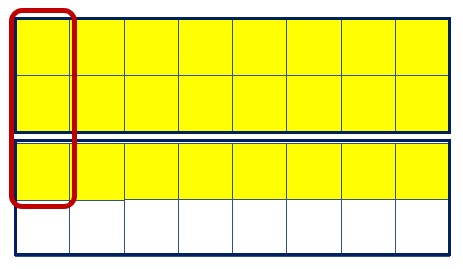
Answer:[latex]\frac{3}{16}[/latex]
This model can be extended to situations where the divisor is a nice fraction. For example, [latex]\frac{6}{7}\div\frac{1}{2}[/latex] can be thought of as
- starting with [latex]\frac{6}{7}[/latex] and
- making [latex]\frac{1}{2}[/latex] a subset/group out of that [latex]\frac{6}{7}[/latex].
If [latex]\frac{6}{7}[/latex] is half a group, then [latex]\frac{12}{7}[/latex] is a whole group. Thus, [latex]\frac{6}{7}\div\frac{1}{2}=\frac{12}{7}[/latex]. This approach quickly becomes difficult if you are trying to solve something like [latex]\frac{53}{12}\div\frac{5}{12}[/latex]. If [latex]\frac{53}{12}[/latex] is [latex]\frac{5}{12}[/latex] of a subset, how much is a full subset? It is not clear. So, we need another approach.
Fraction Division by Repeated Subtraction
Recall the exploratory activity with the quarters. You split the $10 into quarters by finding how many quarters make up $10. That is exactly how the repeated subtraction model works. If we want to solve [latex]\frac{9}{2}\div\frac{3}{4}[/latex] we start by drawing out [latex]\frac{9}{2}[/latex].
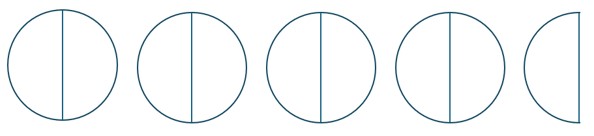
Next, since we are dividing by fourths, we need to break our circles into pieces of size [latex]\frac{1}{4}[/latex].
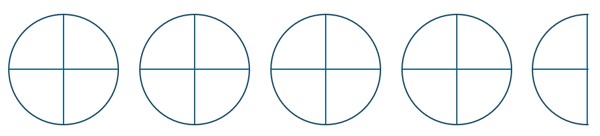
Then, we count how many groups of size [latex]\frac{3}{4}[/latex] we can get out of [latex]\frac{9}{2}[/latex]. This means repeatedly grouping three of our one-fourth pieces until we run out of pieces.
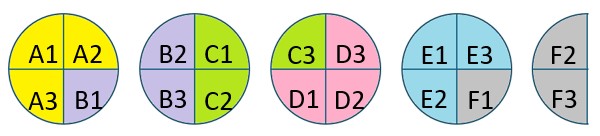
In this case, we can make six groups of size [latex]\frac{3}{4}[/latex]. This means [latex]\frac{9}{2}\div\frac{3}{4}=6[/latex].
We could also have represented the problem on a number-line or using fraction tiles.
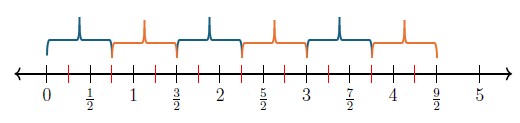
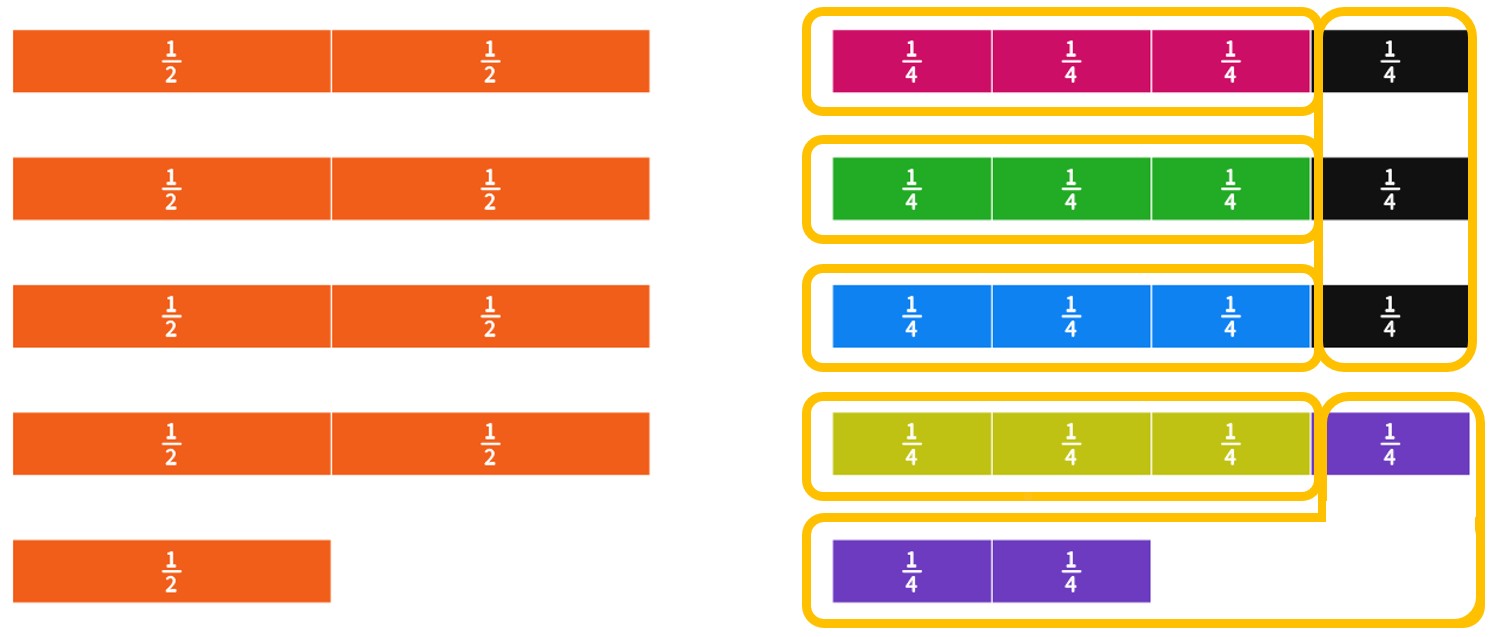
The key is to somehow visualize [latex]\frac{9}{2}[/latex], break it into fourths, and make groups of size [latex]\frac{3}{4}[/latex].
Exercise 8
Evaluate the following division problems using a visual model of repeated subtraction.
a. [latex]\displaystyle 4\div\frac{4}{7}[/latex]
Solution
Answer: 7 groups
b. [latex]\displaystyle 2\frac{1}{2}\div\frac{5}{6}[/latex]
Solution
Answer: 3 groups

c. [latex]\displaystyle \frac{12}{5}\div\frac{3}{10}[/latex]
Solution
Answer: 8 groups

d. [latex]\displaystyle \frac{53}{12}\div\frac{7}{12}[/latex]
Solution
Answer: 7 groups with remainder [latex]\frac{4}{12}[/latex]

Look back at your answer to Exercise 8d. Did you say the answer was [latex]7\frac{4}{12}[/latex]? That is not correct! It may be [latex]7[/latex] with a remainder of [latex]\frac{4}{12}[/latex], but that is not the same as saying there are [latex]7\frac{4}{12}[/latex] groups. Let’s look at how to handle remainder in terms of groups.
We’ll start by looking at how to evaluate [latex]\displaystyle\frac{11}{4}\div\frac{5}{8}[/latex] using a visual model of repeated subtraction. The majority of the work will be the same as what we just did.
First we draw out [latex]\displaystyle\frac{11}{4}[/latex].
Next, we need to split it into eighths since we are dividing by [latex]\displaystyle\frac{5}{8}[/latex].
Now we can make groups of size [latex]\displaystyle\frac{5}{8}[/latex] (i.e. five pieces of size one-eighth).
Notice that we have four full groups and two one-eighth pieces leftover. Let’s think in terms of groups. It would take five one-eighth pieces to make a group, so we have two of the five pieces needed for another group. In other words, we have four full groups and [latex]\frac{2}{5}[/latex] of another group. Thus,
[latex]\displaystyle\frac{11}{4}\div\frac{5}{8}=4\frac{2}{5}[/latex].
Now, let’s revisit Exercise 8, part d.
Example 4
Evaluate [latex]\displaystyle \frac{53}{12}\div\frac{7}{12}[/latex] using a visual model of repeated subtraction.
Solution
Represent [latex]\frac{53}{12}[/latex] and make groups of size [latex]\frac{7}{12}[/latex].

We have 7 full groups and four pieces of size [latex]\frac{1}{12}[/latex] leftover. This means we have 4 of the 7 pieces needed to make a full group.
Answer: [latex]\displaystyle 7\frac{4}{7}[/latex]
Exercise 9
Evaluate each of the following division problems using a visual model of repeated subtraction.
a. [latex]\displaystyle\frac{9}{2}\div\frac{5}{6}[/latex]
Solution
Answer: [latex]5\frac{2}{5}[/latex]
b. [latex]\displaystyle 5\div\frac{2}{3}[/latex]
Solution
Answer: [latex]7\frac{1}{2}[/latex]
c. [latex]\displaystyle\frac{17}{5}\div\frac{3}{10}[/latex]
Solution
Answer: [latex]11\frac{1}{3}[/latex]

Concept Check: When we looked at division of whole numbers, we used remainder to represent the leftover portion in a division problem. Now that we have fractions, we see there are two representations. Explain the difference between [latex]6\frac{3}{4}[/latex] and [latex]6[/latex] remainder [latex]\frac{3}{4}[/latex] as answers to division problems.
Solution
If the answer is [latex]6\frac{3}{4}[/latex] that means there are 6 full groups and three-fourths of another group. It does not tell us how much of a unit we had leftover, only that we have three-fourths of the pieces necessary to make another group.
If the answer is [latex]6[/latex] remainder [latex]\frac{3}{4}[/latex] that means there are 6 full groups and three-fourths of a unit leftover. It does not tell us how much of a group that three-fourths is.
The majority of the time, we want the fraction of a group and not the remainder when dividing fractions. If you are using a calculator to divide fractions, it will give you the “groups” answer and not the “remainder” answer.
Concept Check: When is partitioning into equal subsets useful for dividing fractions? When is repeated subtraction useful for dividing fractions? Will these two models cover all situations?
Solution
If the divisor in our problem is a whole number or a simple fraction like [latex]\frac{1}{2}[/latex], partitioning into equal subsets works.
If the dividend is larger than the divisor and it is easy to break the pieces up into the size the divisor wants, repeated subtraction works.
This definitely does not cover all situations! Things like [latex]\frac{12}{87}\div\frac{59}{60}[/latex] do not fit either of these situations.
Algorithm for Dividing Fractions
One method that does work for all fraction division problems is the “flip and multiply algorithm.” This algorithm was covered in the Pre Unit Review Multiply and Divide Fractions. But now you have a stronger understanding of what division of fractions really means according to our models, so let’s review this algorithm.
Algorithm to Divide Fractions
Let a, b, c, and d be numbers where b and d are not zero. Then
[latex]\displaystyle \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}[/latex].
Consider the rectangle you drew in Exercise 7a. It looks a lot like the rectangle we drew for Exercise 3a. This is because
[latex]\displaystyle\frac{3}{5}\div 6=\frac{3}{5}\div\frac{6}{1}=\frac{3}{5}\times\frac{1}{6}[/latex].
The two problems were actually the same question in different forms!
Exercise 10
Solve [latex]\frac{3}{4}\div 4[/latex] by partitioning into equal subsets, then discuss how your picture is similar to the solution to Exercise 3d.
Solution
For both problems we started by splitting the rectangle into fourths horizontally and shading three of the fourths. Then, for both problems, we split the rectangle into fourths vertically and focus only on one of the four columns made. With the multiplication model, we shaded that one column and counted the number of double shaded pieces. With the partition model, we circled the shaded pieces in that column. But, in both models our answer focused on the same three pieces.
Exercise 11
Solve the following fraction division problems using the “flip and multiply” algorithm.
a. [latex]\displaystyle \frac{9}{2}\div\frac{5}{6}[/latex]
Solution
[latex]\frac{9}{2}\times\frac{6}{5}=\frac{27}{5}[/latex]
b. [latex]\displaystyle 5\div\frac{2}{3}[/latex]
Solution
[latex]\frac{5}{1}\times\frac{3}{2}=\frac{15}{2}[/latex]
c. [latex]\displaystyle \frac{17}{5}\div\frac{3}{10}[/latex]
Solution
[latex]\frac{17}{5}\times\frac{10}{3}=\frac{34}{3}[/latex]
Applications of Fraction Division
Word problems that involve fractions and division are often easier than a problem that is given without context. This is because the information in the problem helps us to draw an accurate picture and get an understanding of what is going on.
Exercise 12
Solve the following word problems.
a. Your cat eats [latex]\frac{3}{4}[/latex] of a cup of a food a day. If you have 7 cups of food in your cupboard, how many days can you feed your cat?
Solution
Let’s solve this problem visually by drawing out the 7 cups of food.
We have 9 full days of food and [latex]\frac{1}{3}[/latex] of a day.
If we solve this using the algorithm, we have
[latex]7\div\frac{3}{4}=7\times\frac{4}{3}=\frac{28}{3}=9\frac{1}{3}[/latex].
Answer: [latex]9 \frac{1}{3}[/latex] days
b. You are in charge of making award ribbons for an upcoming event. You have 10 yards of ribbon and each award needs [latex]\frac{3}{10}[/latex] of a yard of ribbon. How many awards can you make?
Solution
To draw a full picture would be a lot, but we can focus on a portion and go from there. Let’s start with looking at 3 yards of ribbon.

Since we can get 10 awards out of 3 yards with none leftover, that means we can get 30 awards out of 9 yards with none leftover. Now we only need to consider one more yard to reach our total of 10 yards.
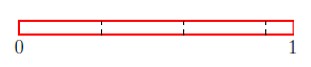
We can get 3 more awards and we have [latex]\frac{1}{10}[\latex] leftover. Thus we can make a total of 33 awards. If we use the algorithm, we have
[latex]10\div\frac{3}{10}=10\times\frac{10}{3}=\frac{100}{3}=33\frac{1}{3}[/latex].
Answer: 33 awards.
Classroom Connection: Roberta is solving the cat word problem from the previous exercise and does the following:
[latex]7\times\frac{3}{4}=\frac{21}{4}=5\frac{1}{4}[/latex].
Use a model of division to explain to Roberta why she should divide instead of multiplying.
Solution
Roberta, let's look at what is physically happening in the problem. We are starting with 7 cans of food and using three-fourths of a can every day. This means we are subtracting three-fourths over and over until we run out of cat food. Repeated subtraction is a model of division, not multiplication. If you are asking, "how many of a number can I measure out of a second number", that is division. If you are repeating a number a known number of times and adding the repeats together, that is multiplication.
Classroom Connection: You are teaching your students to divide fractions and show them that [latex]\frac{1}{2}\div\frac{1}{12}=6[/latex]. Emory raises his hand and says, "How can the answer be larger than what we started with? Doesn't division make things smaller?" How could you help Emory to understand?
Solution
When you divided by whole numbers larger than 1, things got smaller, but fractions are different. Let's think about it this way: [latex]\frac{1}{2}\div\frac{1}{12}[/latex] means "how many one-twelfths can I make out of one-half?" If we divide one-half into twelfths, we see there are six pieces of size one-twelfth. Since we are dividing by such a small number we are able to make a lot of groups, so we end up with a larger number than what we started with! It all depends on if you are dividing by something larger or smaller than 1.
