24 Homework
Use the repeated addition definition of multiplication to compute the following. First, write out the meaning of the multiplication, and then compute the answer.
- [latex]8 \times 4[/latex]
- [latex]4 \times 11[/latex]
2
Use the repeated addition definition of multiplication to compute the following. Make sure you write out the meaning of the multiplication in the system given showing all of the work and exchanges. Do not do the problem in base ten.
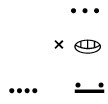
3
Use the definition of multiplication for trains to compute the following. Then translate to make an equation using numbers.
- P [latex]\times[/latex] W [latex]=\underline{\qquad\qquad\qquad}[/latex] which translates to [latex]\underline{\qquad\qquad\qquad}[/latex]
- K [latex]\times[/latex] W [latex]=\underline{\qquad\qquad\qquad}[/latex] which translates to [latex]\underline{\qquad\qquad\qquad}[/latex]
4
Write the Cartesian product
- [latex]\{3,x\}\times\{0,1,6\}[/latex]
- [latex]\{a,b,0\}\times\{1,2\}[/latex]
5
Use the set theory definition of multiplication to verify [latex]3 \cdot 2 = 6[/latex]
6
Complete the following using your base blocks. Show all work.
- F [latex]\times[/latex] L
- C [latex]\times[/latex] L
- F [latex]\times[/latex] F
- F [latex]\times[/latex] C
- C [latex]\times[/latex] F
7
Write the base four multiplication table.
8
Compute the following using the lattice method.
- [latex]2506 \times 451[/latex]
- [latex]2506_{\text{seven}} \times 451_{\text{seven}}[/latex]
9
Compute [latex]19 \times 24[/latex] and [latex]24 \times 19[/latex] using the Duplation method. Show all steps.
10
For each set of three numbers given, illustrate an example of the associative property of multiplication, and then illustrate an example of the distributive property of multiplication over addition. Follow procedures outlined in this module.
- [latex]2_{\text{five}}, 3_{\text{five}}, 4_{\text{five}}[/latex]
- [latex]3_{\text{six}}, 4_{\text{six}}, 5_{\text{six}}[/latex]
