36 Module 7.4 Least Common Multiple and other Topics

Least Common Multiple

There are a finite number of factors for any given number. On the other hand, there are an infinite number of nonzero multiples of a number. For instance the list of multiples of [latex]2[/latex] are all of the even numbers. It's impossible to list all of them, because this is an infinite set. A multiple of a number [latex]c[/latex] is [latex]nc[/latex] where [latex]n[/latex] is a whole number. In other words, to find a multiple of [latex]c[/latex], multiply [latex]c[/latex] by a whole number. Although [latex]0[/latex] is a multiple of every number, we usually omit listing it as a multiple. The (nonzero) multiples of [latex]6[/latex] are listed here:

[latex]6, 12, 18, 24, 30, 36, 42, ...[/latex]

To list the multiples of a number, you begin with the number itself, then the number times [latex]2[/latex], then the number times [latex]3[/latex], etc. Since multiplication is repeated addition, you could repeatedly add the number to get the next multiple.

In exercise 1, we write [latex]LCM(8, 12) = 24[/latex]. The order of the numbers in the parentheses is irrelevant. So, [latex]LCM(8, 12) = LCM(12, 8)[/latex]. It is NOT an ordered pair. Also, you can find the least common multiple of a large set of numbers. Theoretically, we can find the least common multiple of several numbers, such as [latex]LCM(2, 3, 4, 5, 6, 7, 8, 9, 10)[/latex], by listing several (or more) multiples of each of these numbers until we find the smallest one all of them have in common. However, usually this is not the efficient way to find the LCM, so we will be exploring another way to find it using prime factorization.

i. If [latex]x[/latex]and [latex]y[/latex] have no factors in common, that is, [latex]GCF(x,y) = 1[/latex], then [latex]LCM(x,y) = xy[/latex].

ii. If [latex]LCM(x,y) = xy[/latex], then [latex]x[/latex] and [latex]y[/latex] have no factors in common, that is, [latex]GCF(x,y) = 1.[/latex]

A more efficient way to find the least common multiple of a set of numbers is to find the prime factorization of each number, and then BUILD the least common multiple. We will explore this using the prime number squares in your Material Cards.

Below is the prime factorization of three numbers, A, B, and C represented by prime number squares. Below each of them, we write the number in prime factorization form.

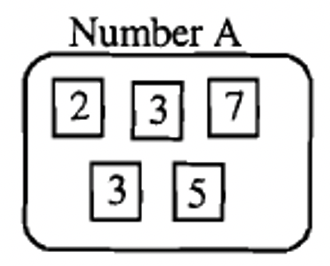[latex]A = 2 \times 3^{2} \times 5 \times 7[/latex]

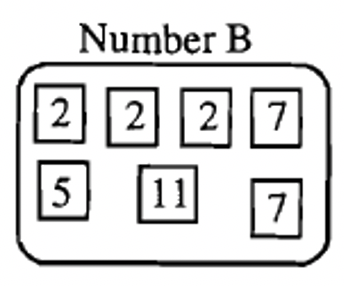[latex]B = 2^{3} \times 5 \times 7^{2} \times 11[/latex]

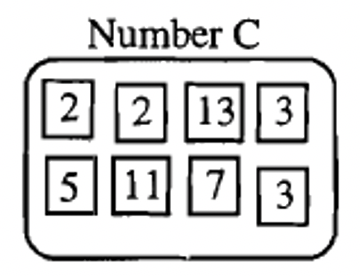[latex]C = 2^{2} \times 3^{2} \times 5 \times 7 \times 11 \times 13[/latex]

Now, we are going to use the prime factorization to build the LEAST COMMON MULTIPLE of a set of numbers. The least common multiple is a multiple that the numbers have in common, but that has the least number of prime factors possible. To build a multiple of a number, we can add one or more prime squares as we want. But differently, to build a least common multiple, we only add a prime factor if it is necessary.

Let's say we want to build the least common multiple of A, B, and C. In order to be a multiple of A, we need to have all the prime factors of A. So, we start building the multiple by putting in the factors of A:

All the prime factors of B must also be in the multiple. B has three factors of [latex]2[/latex], but there is only one [latex]2[/latex] in the multiple so far. So, the common multiple will need two more factors of [latex]2[/latex]. Similarly, B has two prime factors of [latex]7[/latex], but there is only one [latex]7[/latex] in the multiple so far. So, the common multiple will need one more factor of [latex]7[/latex]. B has one factor of [latex]5[/latex], which is already there. B also has one factor of [latex]11[/latex]. That is not there, so it must be put in. Therefore, two factors of [latex]2[/latex], one factor of [latex]7[/latex], and a factor of [latex]11[/latex] must be joined with the other prime factors in the common multiple. Once this is done, we have built the least common multiple of A and B:

The prime factorizations of A, B, and C are shown below for your convenience.

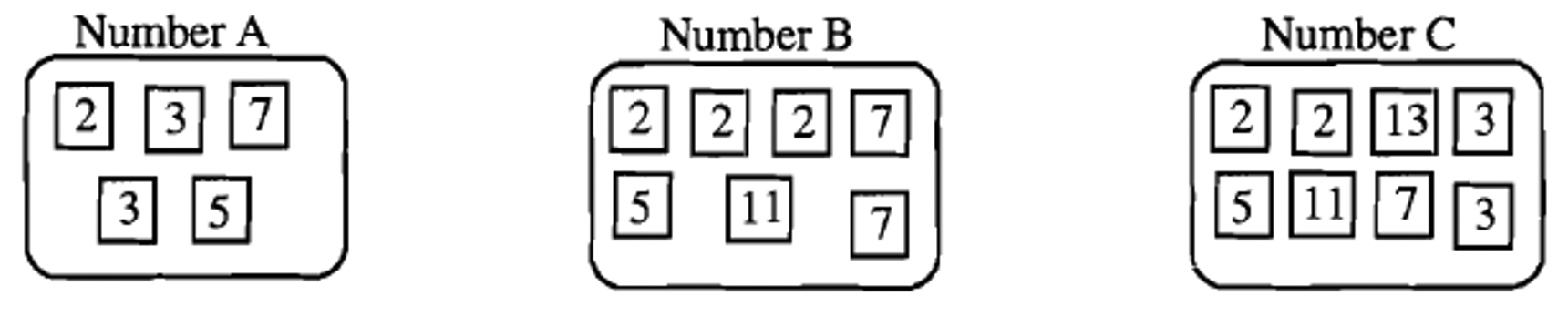
We have built the least common multiple of A and B. To find the least common multiple of A, B, and C, we need to make sure all the prime factors of C are also in the multiple. C has two factors of [latex]2[/latex], which are already in the multiple, two factors of [latex]3[/latex], which are already in the multiple, one factor each of [latex]5, 7,[/latex] and [latex]11[/latex], each of which is already in the multiple, and a factor of [latex]13[/latex], which is not in the multiple. So [latex]13[/latex] is the only prime factor that needs to be joined with the factors already in the multiple we are building.

The above is a multiple of A, B, and C. We not only built a multiple; we actually built the LEAST COMMON MULTIPLE of A, B, and C. Note it is a multiple of A, B, and C; therefore, it is a common multiple. It is the least common multiple because if any of the factors were removed, it wouldn't be a multiple of one of the numbers. For instance, if a factor of [latex]2[/latex] were removed, it would not be a multiple of A. If a factor of [latex]3[/latex] were removed, it would not be a multiple of A or C. If a factor of [latex]7[/latex] were removed, it would not be a multiple of B, etc. If a factor of [latex]11[/latex] were removed, it would not be a multiple of B or C. If a factor of [latex]13[/latex] were removed, it would not be a multiple of C.

We write:

[latex]LCM(A, B, C) = 2^{3} \times 3^{2} \times 5 \times 7^{2} \times 11 \times 13[/latex].

In the exercise below, let's practice more on how to build the least common multiple of numbers with given prime factorization.

[latex]A = 2 \times 5^{3} \times 11 \times 19[/latex] and [latex]B = 2^{4} \times 3^{6} \times 5^{2} \times 23^{2}[/latex] and [latex]C = 5^{4} \times 7^{6} \times 11^{2} \times 23[/latex]

The answer is [latex]LCM(A, B, C) = 2^{4} \times 3^{6} \times 5^{4} \times 7^{6} \times 11^{2} \times 19 \times 23^{2}[/latex]

If the numbers are prime factored using exponents, then the least common multiple contains each of the prime factors shown in any of the numbers, and the exponent on each of the prime numbers is the highest exponent found on that prime number factor in the prime factorization of the numbers.

For instance, the prime numbers in the prime factorization of A, B, and C are [latex]2, 3, 5, 7, 11, 19,[/latex] and [latex]23[/latex]. So begin by writing the product of these prime numbers: [latex]2 \times 3 \times 5 \times 7 \times 11 \times 19 \times 23[/latex]

[latex]2[/latex] is a factor in A and B. The highest power of [latex]2[/latex] found in either prime factorization of A and B is [latex]4[/latex]. [latex]3[/latex] is a factor found in B, as [latex]3^{6}[/latex]. So, the highest power of [latex]3[/latex] is [latex]6[/latex]. [latex]5[/latex] is a factor of all three numbers. In A, the exponent on [latex]5[/latex] is [latex]3[/latex]; in B, the exponent on [latex]5[/latex] is [latex]2[/latex]; in C, the exponent on [latex]5[/latex] is [latex]4[/latex]. So, the highest power of [latex]5[/latex] is [latex]4[/latex]. Similarly, do the same for all of the other prime factors. Write the highest exponent on the factor.

Therefore, [latex]LCM(A, B, C) = 2^{4} \times 3^{6} \times 5^{4} \times 7^{6} \times 11^{2} \times 19 \times 23^{2}[/latex]

So far, the prime factorization of numbers has been given, and all you had to do was build the prime factorization of the least common multiple. Now, your job will be to first prime factor numbers; then you can build the least common multiple from the prime factorizations. In the end, the least common multiple is a number. Multiply the factors in the least common multiple to find the one number that is the least common multiple.

We don't need to expressly write down the prime factorization of the [latex]12[/latex] numbers because it's easy enough to do that in our heads. For instance, the prime factorization of [latex]4[/latex] is [latex]2 \times 2[/latex], the prime factorization of [latex]10[/latex] is [latex]2 \times 5[/latex], and the prime factorization of [latex]13[/latex] is [latex]13[/latex].

We build up the LCM of [latex]2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,[/latex] and [latex]14[/latex] by first making sure the prime factorization of [latex]2[/latex] is there.

Step 1: Make sure the prime factorization [latex]2[/latex] is there. So far, LCM: [latex]2[/latex]

Step 2: Make sure the prime factorization [latex]3[/latex] is there. We need to "throw in" a [latex]3[/latex] to the LCM. So far, LCM: [latex]2 \times 3[/latex]

Step 3: Make sure the prime factorization [latex]4[/latex] is there. We need to "throw in" a [latex]2[/latex] to the LCM. So far, LCM: [latex]2 \times 3 \times 2[/latex]

Step 4: Make sure the prime factorization [latex]5[/latex] is there. We need to "throw in" a [latex]5[/latex] to the LCM. So far, LCM: [latex]2 \times 3 \times 2 \times 5[/latex]

Step 5: Make sure the prime factorization [latex]6[/latex] is there. We don't need to "throw in" any factor(s) to the LCM, so there is no change to the LCM. So far, LCM: [latex]2 \times 3 \times 2 \times 5[/latex].

Step 6: Make sure the prime factorization [latex]7[/latex] is there. We need to "throw in" a [latex]7[/latex] to the LCM. So far, LCM: [latex]2 \times 3 \times 2 \times 5 \times 7[/latex]

Step 7: Make sure the prime factorization [latex]8[/latex] is there. We need to "throw in" a [latex]2[/latex] to the LCM. So far, LCM: [latex]2 \times 3 \times 2 \times 5 \times 7 \times 2[/latex]

Step 8: Make sure the prime factorization [latex]9[/latex] is there. We need to "throw in" a [latex]3[/latex] to the LCM. So far, LCM: [latex]2 \times 3 \times 2 \times 5 \times 7 \times 2 \times 3[/latex]

Step 9: Make sure the prime factorization [latex]10[/latex] is there. We don't need to "throw in" any factor(s) to the LCM, so there is no change to the LCM. So far, LCM: [latex]2 \times 3 \times 2 \times 5 \times 7 \times 2 \times 3[/latex]

Step 10: Make sure the prime factorization [latex]11[/latex] is there. We need to "throw in" an [latex]11[/latex] to the LCM. So far, LCM: [latex]2 \times 3 \times 2 \times 5 \times 7 \times 2 \times 3 \times 11[/latex]

Step 11: Make sure the prime factorization [latex]12[/latex] is there. We don't need to "throw in" any factor(s) to the LCM, so there is no change to the LCM. So far, LCM: [latex]2 \times 3 \times 2 \times 5 \times 7 \times 2 \times 3 \times 11[/latex]

Step 12: Make sure the prime factorization [latex]13[/latex] is there. We need to "throw in" a [latex]13[/latex] to the LCM. So far, LCM: [latex]2 \times 3 \times 2 \times 5 \times 7 \times 2 \times 3 \times 11 \times 13[/latex]

Step 13: Make sure the prime factorization [latex]14[/latex] is there. We don't need to "throw in" any factor(s) to the LCM, so there is no change to the LCM. So far, LCM: [latex]2 \times 3 \times 2 \times 5 \times 7 \times 2 \times 3 \times 11 \times 13[/latex]

That's it! You have now built up the LEAST common multiple of all 12 numbers! You can check to make sure that the prime factorization of each of the 12 numbers is indeed in the prime factorization of the least common multiple you built. Furthermore, if any of the prime factors were removed, it wouldn't be a multiple of all 12 numbers. Therefore, the prime factorization of the LCM is as shown below:

[latex]LCM(2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14) = 2 \times 3 \times 2 \times 5 \times 7 \times 2 \times 3 \times 11 \times 13[/latex]

If these factors are multiplied together,

[latex]LCM(2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14) = 360,360[/latex].

The prime factorization of the LCM may have been written with the factors in ascending order using exponents:

[latex]2^{3} \times 3^{2} \times 5 \times 7 \times 11 \times 13[/latex].

Let's say you know the greatest common factor of [latex]165[/latex] and some other number was [latex]3[/latex], and the least common multiple of the same two numbers was [latex]15015[/latex]. How would you figure out what the other number was?

First, it's a good idea to write down what you know. Let [latex]N[/latex] be the other number.

Then, [latex]GCF(165, N) = 3[/latex] and [latex]LCM (165, N) = 15015[/latex].

Since 3 is a factor, and in fact the greatest common factor, of both [latex]165[/latex] and [latex]N[/latex], then each number can be written as [latex]3[/latex] times something, and the other factor you obtain for [latex]165[/latex] should be relatively prime to the other factor you obtain for [latex]N[/latex], since [latex]3[/latex] is the greatest common factor of [latex]165[/latex] and [latex]N[/latex].

So, let’s rewrite, [latex]LCM (165, N) = 15015[/latex] like this: [latex]LCM (3 \times 55, 3 \times \underline{\qquad}) = 15015[/latex]

In other words, I know [latex]N = 3 \times\underline{\qquad}[/latex], but I have to figure out what goes in the blank to figure out what [latex]N[/latex] is. If you want to introduce another variable, like M, instead of writing a blank, that works just as well. It's up to you.

To find the LCM of [latex]3 \times 55[/latex] and [latex]3 \times \underline{\qquad}[/latex], where the [latex]55[/latex] and the number on the blank have no common factors, you would multiply [latex]3 \times 55 \times\underline{\qquad}[/latex]. But we know the product should be [latex]15015[/latex]. So, the number that must go on the blank must be [latex]91[/latex], since [latex]3 \times 55 times 91 = 15015[/latex]. So, now we can figure out what [latex]N[/latex] is: [latex]N = 3 \times 91 = 273[/latex].

Let's see if this makes sense by first rewriting [latex]165[/latex] and [latex]273[/latex] either in prime factored form or as the [latex]GCF(165, 273)[/latex] times something; then we'll figure out the GCF and LCM from the factored form, and see if it agrees with our original problem.

[latex]165 = 3 \times 55[/latex] and [latex]273 = 3 \times 91[/latex]. First, make sure [latex]3[/latex] is really a factor of each number!

Now, convince yourself that [latex]3[/latex] really is the greatest common factor of [latex]165[/latex] and [latex]273[/latex] by checking to see that the other factor of one number is relatively prime (no factors in common) with the other factor of the other number. So, ask yourself if [latex]55[/latex] and [latex]91[/latex] have any factors in common (besides 1) if you aren't sure, then prime factor each of these numbers first ([latex]55 = 5 \times 11[/latex] and [latex]91 = 7 \times 13[/latex]); note that they have no factors in common.

Since [latex]3[/latex] is the greatest common factor, then the least common multiple is obtained by multiplying [latex]3 \times 55 \times 91[/latex], which is [latex]15015[/latex], which is what it should be according to the original information given. Therefore, [latex]273[/latex] really was the number we were looking for.

There is another way to do the above problem using the following property:

For any two numbers, [latex]m[/latex] and [latex]n[/latex], the following is always true:

[latex]m \times n = GCF(m, n) \times LCM (m, n)[/latex].

The example asks us to verify this property for the given numbers.