35 Primes and Greatest Common Factor
Louisiana Student Standards
Standard Number |
Description of Standard |
| ### | Description |
| ### | Description |
Factors and Prime Numbers
In these first few activities, you'll be using C-strips to explore divisors, factors, prime numbers, and composite numbers.
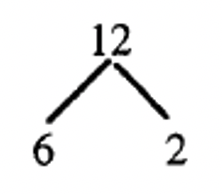
Take out the Hot Pink (H) C-strip, which has a length 12. Use your C-strips (one color at a time) to see if you can form a train made up of C-strips of the same color equal in length to the hot pink C-strip. In other words, see if you can do it with all whites (always possible for any train length), or all reds, or all light greens, etc. You should be able to make six different trains, each train is made up of a single color. Draw a picture of each of these trains under the Hot Pink one shown. I've drawn two trains for you already, one is simply the hot pink strip (a train consisting of just one C-strip), and a second is made up of three purple C-strips.
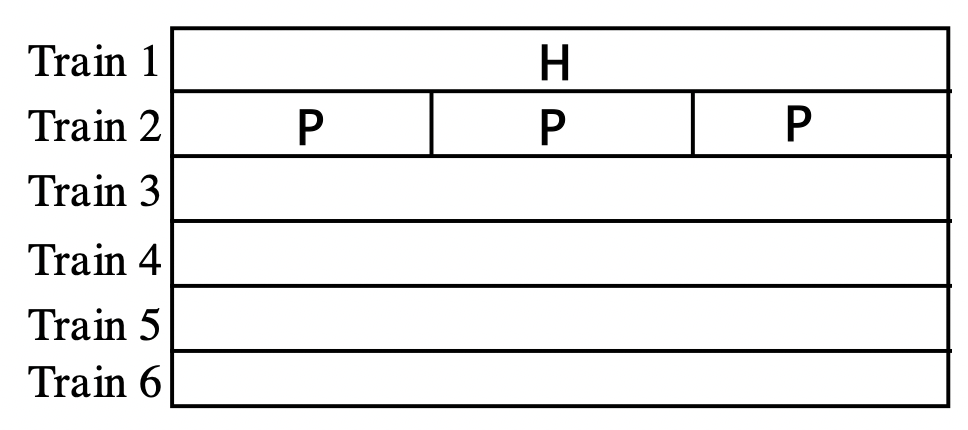
Train 1 illustrates the multiplication [latex]1 \times[/latex]H [latex]=[/latex] H, or [latex]1\times12=12[/latex].
Train 2 illustrates the multiplication [latex]3 \times[/latex] P [latex]=[/latex] H, or [latex]3 \times 4 = 12[/latex].
Train 3 illustrates the multiplication [latex]\underline{\qquad}\times\underline{\qquad}[/latex] = H, or [latex]\underline{\qquad}\times\underline{\qquad}[/latex] = [latex]12[/latex].
Train 4 illustrates the multiplication [latex]\underline{\qquad}\times\underline{\qquad}[/latex] = H, or [latex]\underline{\qquad}\times\underline{\qquad}[/latex] = [latex]\underline{\qquad}[/latex]
Train 5 illustrates the multiplication [latex]\underline{\qquad}\times\underline{\qquad}[/latex] = H, or[latex]\underline{\qquad}\times\underline{\qquad}[/latex] = [latex]\underline{\qquad}[/latex]
Train 6 illustrates the multiplication [latex]\underline{\qquad}\times\underline{\qquad}[/latex] = H, or [latex]\underline{\qquad}\times\underline{\qquad}[/latex] = [latex]\underline{\qquad}[/latex]
The set of numbers placed in the blanks above before the equal sign in the equations with numbers is called factors or divisors of 12. Note that because of the commutative property of multiplication, each factor or divisor was listed twice, representing different one-color trains. Without considering the meanings of the numbers for C-strips, we can list all the factors of 12 as below, from the least to the greatest:
[latex]1, 2, 3, 4, 6, 12[/latex]
Use the same procedure used in Activity 1 to make all possible trains for each of the given lengths. Then, after discovering the possible trains that can be made, list the factors (the actual numbers) of each number from the least to the greatest. Every number greater than 1 has at least two factors.
a. Make one-color trains with a length 2.
List all the factors of 2 : [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
b. Make one-color trains with a length 3.
List all the factors of 3: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
c. Make one-color trains with a length 4.
List all the factors of 4: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
d. Make one-color trains with a length 5.
List all the factors of 5: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
e. Make one-color trains with a length 6.
List all the factors of 6: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
f. Make one-color trains with a length 7.
List all the factors of 7: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
g. Make one-color trains with a length 8.
List all the factors of 8: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
h. Make one-color trains with a length 9.
List all the factors of 9: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
i. Make one-color trains with a length 10.
List all the factors of 10: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
j. Make one-color trains with a length 11.
List all the factors of 11: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
k. Make one-color trains with a length 13.
List all the factors of 13: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
l. Make one-color trains with a length 14.
List all the factors of 14: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
m. Make one-color trains with a length 15.
List all the factors of 15: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
n. Make one-color trains with a length 16.
List all the factors of 16: [latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
Observe the results in Activity 2 and answer the following.
a. List the numbers in Activity 2 that have exactly 2 factors:
[latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
b. What do you notice about the 2 factors each of these numbers has? Is there a pattern or anything they have in common with each other?
c. List numbers from Activity 2 that have an odd number (3 or 5) of factors:
[latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
d. What do all of these numbers have in common?
[latex]\underline{\qquad\qquad\qquad\qquad\qquad\qquad}[/latex]
Definition - Prime Number and Composite Number
A whole number that has exactly two different factors is called a prime number.
Any whole number larger than [latex]1[/latex] that is not prime is called a composite number.
Any whole number larger than [latex]1[/latex] that is not prime is called a composite number. A whole number that has exactly two different factors is called a prime number. That is, if a number is prime, its only factors are [latex]1[/latex] and itself. In other words, if a number, [latex]p[/latex], is prime, its only factors are [latex]1[/latex] and [latex]p[/latex]. If you are using the C-strips and try to make a rectangle out of a train that has a length that is a prime number, the only possibility is when the width is [latex]1[/latex] and the length is the length of the original train. That is because those are the only factors, and no other number divides into them.
Below is the list of all prime numbers less than [latex]16[/latex] that we have found in Activity 3 above:
[latex]2, 3, 5, 7, 11, 13[/latex]
NOTE:
- [latex]0[/latex] is neither prime nor composite.
- [latex]1[/latex] is NOT prime since it doesn't have two different factors it only has one 1, so [latex]1[/latex] is neither prime nor composite. Any whole number larger than [latex]1[/latex] is either prime or composite.
- [latex]2[/latex] is the only even prime number.
If a number is composite, it means that it has more than 2 factors, and can be written as a product of factors less than itself. For instance, [latex]12[/latex] is not a prime number. It can be written as [latex]2\cdot6[/latex] or [latex]3\cdot4[/latex]. This is called factoring, and [latex]2\cdot6[/latex] and [latex]3\cdot 4[/latex] are two ways of factoring 12, or factorization.
Factorizing Numbers
What we are going to do in this section is to factor composite numbers. Any composite number can be factored as a product of two numbers smaller than it. But here the ultimate goal is to factor the number into a product of primes; that is, one of them can be factored further. We call this process prime factoring. For instance, we've factored 12 as [latex]2\cdot6[/latex] and [latex]3\cdot 4[/latex], but both still have a composite factor, respectively, 6 and 4, to allow a further step of factoring:
[latex]12 = 2 \times 6 = 2 \times 2 \times 3[/latex], or [latex]12 = 3 \times 4 = 3 \times 2 \times 2[/latex].
At this point, the composite number is factored as the product of three prime factors. In general, we break down a composite number into two factors, then keep breaking down each until all factors are prime. Example 1 shows the process of prime factoring the number [latex]210[/latex].
Example 1
Prime factor [latex]210[/latex] by breaking it to two factors first then, and show the individual steps.
Solution 1:
[latex]210 = 21 \times 10 = 3 \times 7 \times 2 \times 5[/latex]
Solution 2:
[latex]210 = 2 \times 105 = 2 \times 3 \times 35 = 2 \times 3 \times 5 \times 7[/latex]
Solution 3:
[latex]210 = 30 \times 7 = 5 \times 6 \times 7 = 5 \times 2 \times 3 \times 7[/latex]
Similar to the prime factoring of [latex]12[/latex], there are many other ways one might go about factoring [latex]210[/latex], but in the end, there are 4 prime factors that when multiplied together equal [latex]210[/latex]. Because of the commutative and associative properties of multiplication, [latex]3 \times 7 \times 2 \times 5 = 2 \times 3 \times 5 \times 7 = 5 \times 2 \times 3 \times 7[/latex]. Usually, the primes are written in ascending order (from the smallest factor to the largest factor. We write that the prime factorization of [latex]210[/latex] is [latex]2 \times 3 \times 5 \times 7[/latex].
This leads to a very important theorem. You can think of the prime numbers as building blocks for all whole numbers greater than [latex]1[/latex] under the operation of multiplication. Every whole number greater than [latex]1[/latex] is either prime, or can be expressed as the product of prime factors (called the prime factorization). The fact that any composite number can be written as a unique product of primes is so important that it is called the Fundamental Theorem of Arithmetic.
Key Takeaway - The Fundamental Theorem of Arithmetic
Every composite number has exactly one unique prime factorization (except for the order in which the factors are written.)
Note again that the order in which the factors are written doesn't matter, which is guaranteed by the commutative and associative properties of multiplication. However, for consistency, they are usually written in ascending order (from least to greatest). Also, exponents may be used if a factor is repeated in the prime factorization. For instance, the prime factorization of [latex]12[/latex] is usually written as [latex]2 \times 2 \times 3[/latex] or [latex]2^{2} \times 3[/latex].
For the given composite number, follow the procedure of Example 1 to write it as a product of two factors first, then keep factoring each factor until all factors are prime. Write the prime factorization so the factors are written in ascending order (from smallest to largest). Show each of the individual steps one at a time, not just the final product.
(Note: The solutions will vary in some problems, but the final answers will be the same.)
a. 45
Solution
[latex]45 = 5 \times 9 = 5 \times 3 \times 3 = 3^{2} \times 5[/latex]
b. 65
Solution
[latex]65 = 5 \times 13[/latex]
c. 200
Solution
[latex]200 = 2 \times 100 = 2 \times 10 \times 10 = 2 \times 2 \times 5 \times 2 \times 5 = 2^{3} \times 5^{2}[/latex]
d. 91
Solution
[latex]91 = 7 \times 13[/latex]
e. 76
Solution
[latex]76 = 2 \times 38 = 2 \times 2 \times 19 = 2^{2} \times 19[/latex]
f. 350
Solution
[latex]350 = 10 \times 35 = 2 \times 5 \times 5 \times 7 = 2 \times 5^{2} \times 7[/latex]
g. 189
Solution
[latex]189 = 9 \times 21 = 3 \times 3 \times 3 \times 7 = 3^{3} \times 7[/latex]
h. 74
Solution
[latex]74 = 2 \times 37[/latex]
i. 512
Solution
[latex]512 = 4 \times 128 = 2 \times 2 \times 4 \times 32 = 2 \times 2 \times 2 \times 2 \times 4 \times 8[/latex]
[latex]= 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 4[/latex]
[latex]= 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^{9}[/latex]
j. 147
Solution
[latex]147 = 7 \times 21 = 7 \times 3 \times 7 = 3 \times 7^{2}[/latex]
There are other methods commonly used to find the prime factorization. One is called a FACTOR TREE, which presents the breaking down process as a tree shape: The number you are trying to factor is like the "root" of the tree, but is placed at the top; so, it's actually an upside-down tree. Then we draw two "branches" down to the two factors we get in the first breaking down. If a number at a branch is not prime, we draw two branches down from that number and factor it as the product of any two factors. At the end of each branch is a smaller factor, which is like "a leaf". If a leaf is prime, circle it, and it is one of the factors in the prime factorization of the number. Otherwise, branch off again. When all of the leaves are circled prime numbers, you are done. The prime factorization of the root is the product of the prime leaves.
Example 2
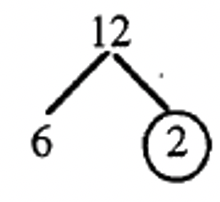
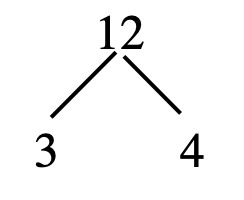
Use a factor tree to show the prime factoring of [latex]12[/latex], [latex]12 = 3 \times 4 = 3 \times 2 \times 2 = 2^{2} \times 3[/latex].
Solution:
Step 1: Factor [latex]12[/latex] as [latex]3 \times 4[/latex]. Now the factor tree looks like this:
Step 2: Circle [latex]3[/latex] since it is prime.
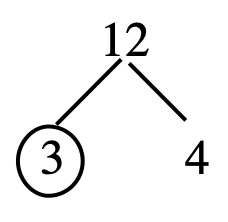
Step 3: Factor [latex]4[/latex] as [latex]2 \times 2[/latex].
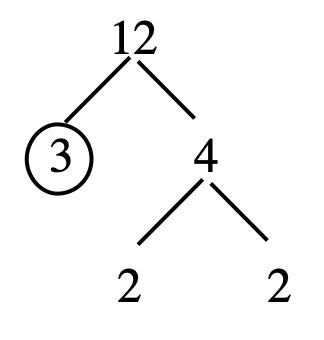
Step 4: Circle the [latex]2[/latex]s since they are prime.
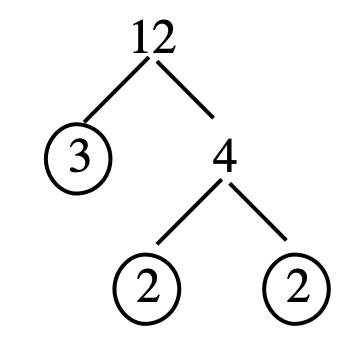
Step 5: The prime factorization of [latex]12[/latex] is the product of the circled leaves: [latex]2 \times 2 \times 3[/latex]. We write this as:
[latex]12 = 2 \times 2 \times 3= 2^{2} \times 3[/latex]
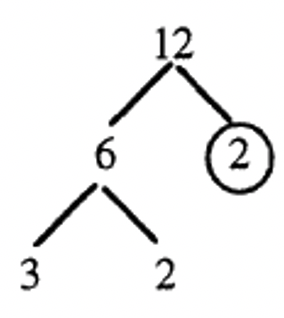
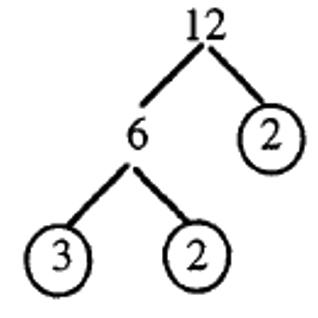
Below is the other way we factored [latex]12[/latex] shown by a factor tree. Notice that the two-factor trees for [latex]12[/latex] have the same root, [latex]12[/latex], and the same prime leaves, [latex]2, 2, 3[/latex], with different details.
|
Steps |
Factor Tree |
|---|---|
|
Step 1: Facrtor [latex]12[/latex] as [latex]6 \times 2[/latex]. |
|
|
Step 2: Circle [latex]2[/latex] since it is prime. |
|
|
Step 3: Factor [latex]6[/latex] as [latex]2 \times 3[/latex] |
|
|
Step 4: Circle [latex]3[/latex] and [latex]2[/latex] since they are both prime. |
|
|
Step 5: The prime factorization of [latex]12[/latex] is the product of the circled leaves [latex]3 \times 2 \times 2[/latex] |
[latex]12 = 2 \times 2 \times 3 = 2^{2} \times 3[/latex] |
When we prime factor a number, it is important to determine if a factor is prime or not. If you aren't sure whether a number is prime or composite and don't know how to start factoring, use the divisibility tests to see if it is possible to divide by [latex]2, 3, 5, 7, 11,[/latex] etc. Make sure there are no factors before you circle it and decide it's prime. Now, for each of the numbers you've worked on in Exercise 1, show your work using a factor tree.
Use a factor tree to factor each of the following composite numbers from exercise 1 into a product of primes. Write the prime factorization so the factors are written in ascending order (from smallest to largest).
a. [latex]45[/latex]
Solution
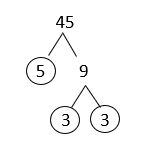
The answer is: [latex]45 = 3^{2} \times 5[/latex]
b. [latex]65[/latex]
Solution
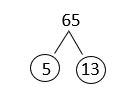
The answer is [latex]65 = 5 \times 13[/latex]
c. [latex]200[/latex]
Solution
The answer is: [latex]200 = 2^{3} \times 5^{2}[/latex]
d. [latex]91[/latex]
Solution
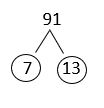
The answer is: [latex]91 = 7 \times 13[/latex]
e. [latex]76[/latex]
Solution
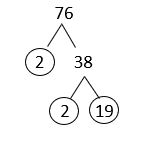The answer is: [latex]76 = 2^{2} \times 19[/latex]
f. [latex]350[/latex]
Solution
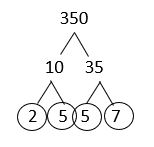
The answer is: [latex]350 = 2 \times 5^{2} \times 7[/latex]
g. [latex]189[/latex]
Solution
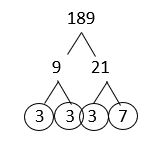
The answer is: [latex]189 = 3^{3} \times 7[/latex]
h. [latex]74[/latex]
Solution
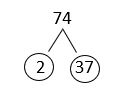
The answer is: [latex]74 = 2 \times 37[/latex]
i. [latex]512[/latex]
Solution
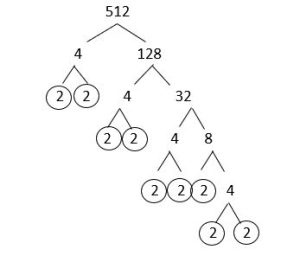
The answer is: The answer is: [latex]512 = 2^{9}[/latex]
j. [latex]147[/latex]
Solution
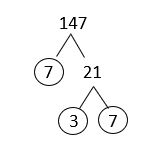
The answer is: [latex]147 = 3 \times 7^{2}[/latex]
Prime Factor Test
The problem with trying to find the prime factorization is that sometimes it isn't obvious if a number you are trying to factor is prime or not. For instance, it is not immediately obvious whether or not 517 is prime or composite. This is where divisibility tests come in handy. However, when the number is large, such as 517, the divisibility tests are not enough for us.
Actually, if you want to find the prime factorization of 517, you only need to check if 517 has any prime numbers as factors. You'll need to try one prime at a time. Before we can do that, we need a list of prime numbers. Example 3 helps us to "sieve out" all the primes less than 100 on a hundred board.
List all of the prime numbers less than [latex]100[/latex] using the hundred chart. You only need to use the divisibility tests for [latex]2, 3, 5[/latex] and [latex]7[/latex] at the most to check if any odd number less than [latex]100[/latex] is prime. In other words, any composite number less than [latex]100[/latex] has [latex]2, 3, 5[/latex] or [latex]7[/latex] as a factor. We'll discuss the reason of it afterward.
Solution:
We list out prime numbers up to [latex]13[/latex], which we have found earlier in this section:
[latex]2, 3, 5, 7, 11, 13[/latex]
Now on the hundred board, we highlight the six primes we have found and cross out those numbers less than [latex]13[/latex] that are not prime. The hundred board looks like this:
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Now, among all the numbers that are greater than [latex]13[/latex], cross all multiples of [latex]2[/latex], which means they are composite, not prime. The hundred board will become this:
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 15 | 17 | 19 | |||||
| 21 | 23 | 25 | 27 | 29 | |||||
| 31 | 33 | 35 | 37 | 39 | |||||
| 41 | 43 | 45 | 47 | 49 | |||||
| 51 | 53 | 55 | 57 | 59 | |||||
| 61 | 63 | 65 | 67 | 69 | |||||
| 71 | 73 | 75 | 77 | 79 | |||||
| 81 | 83 | 85 | 87 | 89 | |||||
| 91 | 93 | 95 | 97 | 99 |
Next step, among the numbers greater than [latex]13[/latex], cross all multiples of [latex]3[/latex] because they are composite. While we are crossing them one by one, we notice that some numbers have already been crossed out, such as [latex]18, 24, 36[/latex], etc. After crossing out all multiples of [latex]3[/latex], the hundred board becomes this:
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 25 | 29 | |||||||
| 31 | 35 | 37 | 3 |
||||||
| 41 | 43 | 47 | 49 | ||||||
| 53 | 55 | 59 | |||||||
| 61 | 65 | 67 | |||||||
| 71 | 73 | 77 | 79 | ||||||
| 83 | 85 | 89 | |||||||
| 91 | 95 | 97 |
When crossing out all multiples of [latex]5[/latex], we notice that, again, many of them are also multiples of [latex]2[/latex] and/or [latex]3[/latex] (such as [latex]20, 30, 40, 45[/latex], etc), and they have been crossed out already. Now we get:
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 29 | ||||||||
| 31 | 37 | 3 |
|||||||
| 41 | 43 | 47 | 49 | ||||||
| 53 | 59 | ||||||||
| 61 | 67 | ||||||||
| 71 | 73 | 77 | 79 | ||||||
| 83 | 89 | ||||||||
| 91 | 97 |
Now among all the numbers that are greater than [latex]13[/latex], cross out all multiples of [latex]7[/latex]. One more time, many numbers have been crossed out as multiples of [latex]2[/latex], or [latex]3[/latex], or [latex]5[/latex]. It is important to notice that the first number that we cross in this round is [latex]49[/latex], which is [latex]7 \times 7[/latex]. And next one to be cross out is [latex]77=7 \times 11[/latex], and then [latex]91=7 \times 13[/latex]. Other than these three, all the other multiples of [latex]7[/latex] have been crossed out in the round for [latex]2, 3[/latex], or [latex]5[/latex]. Now we get
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 29 | ||||||||
| 31 | 37 | 3 |
|||||||
| 41 | 43 | 47 | |||||||
| 53 | 59 | ||||||||
| 61 | 67 | ||||||||
| 71 | 73 | 79 | |||||||
| 83 | 89 | ||||||||
| 97 |
Now we can claim that all numbers left on the board uncrossed are primes. We highlight all the uncrossed numbers to indicate that they are all the primes less than [latex]100[/latex]:
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 29 | ||||||||
| 31 | 37 | 3 |
|||||||
| 41 | 43 | 47 | |||||||
| 53 | 59 | ||||||||
| 61 | 67 | ||||||||
| 71 | 73 | 79 | |||||||
| 83 | 89 | ||||||||
| 97 |
List all the primes less than [latex]100[/latex] from the least to the greatest:
[latex]2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97[/latex]
Why can we make a claim in Example 3 that after this round of crossing out, all numbers left would be prime? In other words, why does any composite number less than [latex]100[/latex] have [latex]2, 3, 5[/latex] or [latex]7[/latex] as a factor? Let's reflect on what we did when crossing out the multiples of [latex]7[/latex]. We've noticed that the first number crossed out only because of [latex]7[/latex] is [latex]7^{2}=7 \times 7[/latex]. This shows that all other multiples of [latex]7[/latex], including [latex]14, 21, 28, 35, 42[/latex], are multiples of primes less than [latex]7[/latex] and were crossed out in the first several rounds. Similarly, for the next prime number after [latex]7[/latex], which is [latex]11[/latex], the first composite number that is not a multiple of [latex]2, 3, 5[/latex], or [latex]7[/latex] would be [latex]11^{2}[/latex], or [latex]121[/latex]. In other words, all numbers less than [latex]121[/latex] must be either prime or a multiple of [latex]2, 3, 5[/latex], or [latex]7[/latex]. This realization makes it easier to determine if a large number is prime or composite, and therefore, makes finding the prime factorization of a number much easier. It is called the Prime Factor Test. This is the formal way of stating that theorem.
Key Takeaway - Prime Factor Test
Prime Factor Test: To test for prime factors of a number [latex]n[/latex], one need only search for prime factors [latex]p[/latex] of [latex]n[/latex], where [latex]p^{2} \leq n[/latex] ( or [latex]p \leq \sqrt{n}[/latex])
According to the prime factor test, we can get the following statements:
i. Since [latex]3^{2} = 9[/latex], any composite number <[latex]9[/latex] has [latex]2[/latex] as a factor. In other words, if a number less than [latex]9[/latex] does not have [latex]2[/latex] as a factor, then it must be prime, such as [latex]5[/latex] and [latex]7[/latex].
ii. Since [latex]5^{2} = 25[/latex], any composite number <[latex]25[/latex] has [latex]2[/latex] or [latex]3[/latex] as a factor. In other words, if neither [latex]2[/latex] nor [latex]3[/latex] is a factor of a number between [latex]9[/latex] and [latex]25[/latex], then it must be prime. For instance: [latex]11, 13, 17, 19[/latex], and [latex]23[/latex].
iii. Since [latex]7^{2} = 49[/latex], any composite number <[latex]49[/latex] has [latex]2, 3[/latex] or [latex]5[/latex] as a factor. In other words, any of the numbers between [latex]25[/latex] and [latex]49[/latex] is either a multiple of [latex]2[/latex], or [latex]3[/latex], or [latex]5[/latex], or a prime.
iv. Since [latex]11^{2} = 121[/latex], any composite number <[latex]121[/latex] has [latex]2, 3, 5[/latex] or [latex]7[/latex] as a factor. In other words, if a number is not a multiple of any of the four primes, it must be prime. That's why we can highlight all the leftover numbers on the hundred board in Example 3.
The four statements above can help us check if a number less than [latex]100[/latex] is a prime or not, without memorizing the list of primes we got in Example 3. Now we can use the prime factor test to determine if [latex]517[/latex] is prime, and if it is not prime, we can then find its prime factorization.
Example 4
Determine if [latex]517[/latex] is prime. If not, find the prime factorization of it.
Solution:
Step 1: Decide which primes we should check.
We need to test the divisibility of [latex]517[/latex] by all primes that are less than the square root of [latex]517[/latex].
Using calculator, we can find [latex]\sqrt{517} \approx{22.7}[/latex], and all the primes less than it are:
[latex]2, 3, 5, 7, 11, 13, 17[/latex], and [latex]19[/latex].
Step 2: Check the divisibility of this number by the primes using the divisibility tests.
By observing the last digit of [latex]517[/latex], we know that [latex]2[/latex] and [latex]5[/latex] are not factor of [latex]517[/latex].
The digital root of [latex]517 = 13 \rightarrow 4[/latex] is not divisible by [latex]3[/latex], so [latex]3[/latex] is not factor of [latex]517[/latex] either.
For [latex]7[/latex]: Double the last digit, [latex]7[/latex], we get [latex]14[/latex]. Then we subtract [latex]14[/latex] from [latex]51[/latex] and get [latex]37[/latex], which is not divisible by [latex]7[/latex], so [latex]7[/latex] is not a factor of [latex]517[/latex] either.
For [latex]11[/latex]: Add the digits in the place that are even powers of [latex]10[/latex], that is [latex]5 + 7 = 12[/latex]. Then subtract the digit in the place that is an odd power of [latex]10[/latex], which gives us [latex]12 - 1 = 11[/latex]. Since [latex]11[/latex] is divisible by [latex]11[/latex], then [latex]517[/latex] is divisible by [latex]11[/latex].
Step 3: Conclude if the number is prime or composite. If it is composite, prime factor it.
Therefore, [latex]517[/latex] is composite.
To factor it, we start with the first factor we just found, [latex]11[/latex]. To find another factor, we divide [latex]517[/latex] by [latex]11[/latex] and get [latex]47[/latex]. So, [latex]517=11 \times 47[/latex].
Now we look at the other factor, [latex]47[/latex]. As a number less than [latex]49=7^2[/latex], we can have a quick check for the divisibility of it by [latex]2, 3[/latex], and [latex]5[/latex], to find out that it is prime.
As a conclusion, the prime factorization of [latex]517[/latex] is:
[latex]517=11 \times 47[/latex]
Now follow the steps in Example 4 to complete Exercise 3.
Exercise 3
For each number, determine the highest prime that might need to be checked to find the prime factorization of the number. Then, find the prime factorization. If it is prime, simply write the number itself, since that is the prime factorization.
a.
The prime factorization for [latex]149[/latex] is:
Solution
[latex]149[/latex]
b.
The prime factorization for [latex]273[/latex] is:
Solution
[latex]273 = 3 \times 7 \times 13[/latex]
c.
The prime factorization for [latex]381[/latex] is:
Solution
[latex]381 = 3 \times 127[/latex]
d.
The prime factorization for [latex]437[/latex] is:
Solution
[latex]437= 19 \times 23[/latex]
e.
The prime factorization for [latex]509[/latex] is:
Solution
[latex]509[/latex]
f.
The prime factorization for [latex]527[/latex] is:
Solution
[latex]527= 17 \times 31[/latex]
g.
The prime factorization for [latex]613[/latex] is:
Solution
[latex]613[/latex]
Now, let's look at a range of numbers and figure out how to determine which ones are prime. For instance, let's determine which numbers between [latex]350[/latex] and [latex]370[/latex] are prime. First of all, only odd numbers in this range are prime. So, begin by listing the odd numbers as possibilities: [latex]351, 353, 355, 357, 359, 361, 363, 365, 367[/latex] and [latex]369[/latex]. Next, note that [latex]355[/latex] and [latex]365[/latex] can't be prime since both are divisible by [latex]5[/latex]. Now, you might use the divisibility test for [latex]3[/latex] to cross off [latex]351, 357, 363[/latex] and [latex]369[/latex]. (Note: you can cross off multiples of [latex]3[/latex] by crossing off every third odd number if you start at a multiple of [latex]3[/latex]. Now, our list is down to these possibilities: [latex]353, 359, 361, 367[/latex] and [latex]369[/latex]. The highest prime you'd have to check is the prime number that is less than the square root of [latex]369[/latex], which is [latex]19[/latex]. So, simply check the rest of the primes ([latex]7, 11, 13, 17[/latex] and [latex]19[/latex] at most) on each of these numbers to determine which, if any, are prime. [latex]353[/latex] is prime; [latex]359[/latex] is prime; [latex]361[/latex] is composite because [latex]19[/latex] is a factor, and [latex]367[/latex] is prime. Therefore, [latex]353, 359[/latex] and [latex]367[/latex] are the numbers between [latex]350[/latex] and [latex]370[/latex] that are prime. Furthermore, you should be able to write the prime factorization for all the numbers between [latex]350[/latex] and [latex]370[/latex] that are composite.
Find the prime factorization for all the numbers between [latex]280[/latex] and [latex]295[/latex]. If a number is prime, simply write the number itself.
a. [latex]280[/latex]
Solution
[latex]280 = 2^{3} \times 5 \times 7[/latex]
b. [latex]281[/latex]
Solution
[latex]281[/latex]
c. [latex]282[/latex]
Solution
[latex]282 = 2 \times 3 \times 47[/latex]
d. [latex]283[/latex]
Solution
[latex]283[/latex]
e. [latex]284[/latex]
Solution
[latex]284 = 2^{2} \times 71[/latex]
f. [latex]285[/latex]
Solution
[latex]285 = 3 \times 5 \times 19[/latex]
g. [latex]286[/latex]
Solution
[latex]286 =2 \times 11 \times 13[/latex]
h. [latex]287[/latex]
Solution
[latex]287 = 7 \times 41[/latex]
i. [latex]288[/latex]
Solution
[latex]288 = 2^{5} \times 3^{2}[/latex]
j. [latex]289[/latex]
Solution
[latex]289 = 17^{2}[/latex]
k. [latex]290[/latex]
Solution
[latex]290 = 2 \times 5 \times 29[/latex]
l. [latex]291[/latex]
Solution
[latex]291 = 3 \times 97[/latex]
m. [latex]292[/latex]
Solution
[latex]292 = 2^{2} \times 73[/latex]
n. [latex]293[/latex]
Solution
[latex]293[/latex]
o. [latex]294[/latex]
Solution
[latex]294 = 2 \times 3 \times 7^{2}[/latex]
p. [latex]295[/latex]
Solution
[latex]295 = 5 \times 59[/latex]
Further Exploration
Twin primes are two consecutive odd numbers that are prime. For instance, [latex]5[/latex] and [latex]7[/latex] are twin primes, [latex]11[/latex] and [latex]13[/latex] are twin primes, [latex]17[/latex] and [latex]19[/latex] are twin primes. There is no pattern to determine how often twin primes come up. One unsolved question in mathematics is whether there are a finite number of or infinitely many sets of twin primes.
More to work on:
i. From your work in exercise 11, list any sets of twin primes: _____
ii. Is it possible to have three odd numbers in a row that are prime? Why or why not?
Greatest Common Factor (GCF)
One use of prime factoring a set of numbers is so you can find the greatest common factor (GCF) and the least common multiple (LCM) of them. Many people have trouble distinguishing between the greatest common factor and the least common multiple (LCM) because they don't think about what the words actually mean. The greatest common factor of a number is obviously a factor, but the adjective common describes that you want a factor that is common to all the numbers, and the adjective greatest describes that you want the very largest of the common factors of the numbers.
We are going to explore ways of finding the greatest common factor of two numbers, a and b. The notation to express this is GCF(a, b). It doesn't matter which number you list first in the parentheses – it's not an ordered pair.
Definition - Greatest Common Factor
The greatest common factor of a set of numbers is the largest number that is a factor of each number.
We use the notation [latex]GCF(a, b)[/latex] for the greatest common factor of two numbers [latex]a[/latex] and [latex]b[/latex].
We are going to explore different ways of finding the greatest common factor of two numbers.
First, we are going to explore one way to find the greatest common factor of [latex]42[/latex] and [latex]72[/latex]. The notation to express this is GCF([latex]42, 70[/latex]).
Remember: it doesn't matter which number you list first in the parentheses; it's not an ordered pair. GCF([latex]42, 70[/latex]) means the same thing as GCF([latex]70, 42[/latex]). Both of them mean the greatest common factor of [latex]42[/latex] and [latex]70[/latex] is the largest number that is a factor of both [latex]42[/latex] and [latex]70[/latex].
One way of doing this is to list every single factor of each number and then pick the biggest one that is a factor of each.
Find GCF ([latex]42, 70[/latex]).
Solution:
Step 1: List all of the factors of [latex]42[/latex] in ascending order:
[latex]42: \{1, 2, 3, 6, 7, 14, 21, 42\}[/latex]
Step 2: List all of the factors of [latex]70[/latex] in ascending order:
[latex]70: \{1, 2, 5, 7, 10, 14, 35, 70\}[/latex]
Step 3: List all of the factors that are common to both [latex]42[/latex] and [latex]70[/latex]:
[latex]\{1, 2, 7, 14\}[/latex]
Step 4: Find the greatest common factor listed in Step 3 and make the conclusion:
[latex]GCF(42, 70)=14[/latex]
Listing all of the factors of a given number is sometimes a difficult task. For instance, it's easy to miss a factor. One remedy is to prime factor the number first. To list all of the factors of [latex]42[/latex], one might first prime factor [latex]42[/latex] like this: [latex]2 \times 3 \times 7[/latex]. For a number to be a factor of [latex]42[/latex], it must be composed of the prime factors listed. Of course, [latex]1[/latex] is always a factor. Next, you'd check [latex]2[/latex], and then [latex]3[/latex], which are both factors. [latex]4[/latex] is not a factor because if it were, [latex]2 \times 2[/latex] would be in the prime factorization! It's clear to see [latex]5[/latex] is not a factor. [latex]6[/latex] is a factor, since [latex]2 \times 3[/latex] is in the prime factorization. Continuing on, [latex]7[/latex] is a factor, but [latex]8[/latex] is not because [latex]2 \times 2 \times 2[/latex] is not in the prime factorization of [latex]42[/latex]. Neither is [latex]9[/latex] ([latex]3 \times 3[/latex]), [latex]10[/latex] ([latex]2 \times 5[/latex]), [latex]11[/latex], [latex]12[/latex] ([latex]2 \times 2 \times 3[/latex]), or [latex]13[/latex]. But [latex]14[/latex] is a factor of [latex]42[/latex] since [latex]2 \times 7[/latex] is in the prime factorization.
You can use this strategy as you check every number up to [latex]42[/latex], but that is still a lot of numbers to check, which you don't have to do. Here's a way to shorten the process a little more. Starting with the smallest factor [latex]1[/latex], immediately list the other factor you'd have to multiply by that factor to get [latex]42[/latex]. So, we start with [latex]\{1, 42\}[/latex]. We check the next number, [latex]2[/latex], and note it is a factor. To get the other factor that pairs up with [latex]2[/latex], either divide [latex]2[/latex] into [latex]42[/latex], or simply look at the prime factorization of [latex]42[/latex], with the [latex]2[/latex] missing. There is [latex]3 \times 7[/latex] left, which is the other factor. So the list is now [latex]\{1, 42, 2, 21\}[/latex].
Continuing, we note [latex]3[/latex] is a factor. To get the other factor, either divide [latex]42[/latex] by [latex]3[/latex], or do it the easy way, which is to see what factors are left in the prime factorization of [latex]42[/latex] with the [latex]3[/latex] missing. Since there is a [latex]2[/latex] and a [latex]7[/latex], then the number that pairs up with [latex]3[/latex] is [latex]14[/latex]. The list is now [latex]\{1, 42, 2, 21, 3, 14\}[/latex].
Next, we note [latex]4[/latex] and [latex]5[/latex] are not factors. [latex]6[/latex] is a factor since [latex]2[/latex] and [latex]3[/latex] ([latex]2 \times 3[/latex]) is in the prime factorization. [latex]7[/latex] is the number that pairs up with [latex]6[/latex]. So, the list is now: [latex]\{1, 42, 2, 21, 3, 14, 6, 7\}[/latex]. If you were to continue, the next number to check would be [latex]7[/latex], and it leads you back to the factor [latex]6[/latex], which means we can stop. All the factors that are larger than [latex]7[/latex] will already be in the list because there would have been a smaller factor that it paired up with already. Now, put the list of factors of [latex]42[/latex] in ascending order: [latex]\{1, 2, 3, 6, 7, 14, 21, 42\}[/latex].
The same procedure can be used to list all the factors of [latex]70[/latex]. First, write the prime factorization of [latex]70[/latex]: [latex]2 \times 5 \times 7[/latex]. You would start off with [latex]1[/latex] and [latex]70[/latex] for a set of: [latex]\{1, 70\}[/latex]. Next, it's clear [latex]2[/latex] is a factor that pairs up with [latex]35[/latex]. The list is now: [latex]\{1, 70, 2, 35\}[/latex]. Next discard [latex]3[/latex] and [latex]4[/latex] as factors, and note [latex]5[/latex] is a factor. The factors left are [latex]2[/latex] and [latex]7[/latex], which multiplied together is [latex]14[/latex]. So the list is [latex]\{1, 70, 2, 35, 5, 14\}[/latex]. Continuing on, note [latex]6[/latex] is not a factor, and [latex]7[/latex] is. [latex]7[/latex] pairs up with [latex]10[/latex]. The list is now: [latex]\{1, 70, 2, 35, 5, 14, 7, 10\}[/latex]. Continuing on, note that [latex]8[/latex] is not a factor. The next number to check would be [latex]9[/latex]. But [latex]9^{2} \gt 70[/latex], so all the factors higher are already in the list. Writing the list in ascending order, we get: [latex]\{1, 2, 5, 7, 10, 14, 35, 70\}[/latex].
Make a note that in both of these examples, [latex]42[/latex] and [latex]70[/latex] each had exactly [latex]3[/latex] prime numbers in the prime factorization. Let's work on a number with more prime factors.
Example 6
Find all factors of [latex]220[/latex] in ascending order using the prime factorization [latex]220=2 \times 2 \times 5 \times 11[/latex].
Solution:
Step 1: The first pair of factors is always [latex]1[/latex] and the number itself.
[latex]1[/latex] and [latex]220[/latex].
Step 2: List other factors in pairs.
Start from combining one, two, or three prime factors to get a leading factor of each pair, then multiply the others to get another factor of this pair.
[latex]2[/latex] is a factor; its pair is [latex]2 \times 5 \times 11 = 110[/latex].
[latex]4 = 2 \times 2[/latex] is a factor; its pair is [latex]5\times 11 = 55[/latex].
[latex]5[/latex] is a factor; its pair is [latex]2 \times 2 \times 11 = 44[/latex].
[latex]10 = 2 \times 5[/latex] is a factor; its pair is [latex]2 \times 11 = 22[/latex].
[latex]11[/latex] is a factor; its pair is [latex]2 \times 2 \times 5 = 20[/latex].
Step 3: Stop and list all factors.
Notice that the leading factors of the pairs are called out in ascending order, whereas their pairs are in descending order. Now, if we move on to make up more factors, such as [latex]2 \times 11 = 22[/latex], or [latex]2 \times 2 \times 5 = 20[/latex], we would find them already shown in the previous pairs. That's the moment that we should stop because we have already found all factors of [latex]220[/latex] as below:
[latex]\{1, 220, 2, 110, 4, 55, 5, 44, 10, 22, 11, 20\}[/latex]
Then we write these in ascending order, we get all the factors of [latex]220[/latex] as below:
[latex]\{1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220\}[/latex]
Now, do the next exercises using the prime factorization to help solve the problem.
Find the greatest common factor of [latex]92[/latex] and [latex]115[/latex].
a. Find the prime factorization of [latex]92[/latex].
Solution
[latex]92 = 2 \times 2 \times 23[/latex]
b. List all of the factors of [latex]92[/latex] in ascending order.
Solution
[latex]92: \{1, 92, 2, 46, 4, 23\}[/latex] are the pairs listed together
[latex]92: \{1, 2, 4, 23, 46, 92\}[/latex] are the factors listed in ascending order
c. Find the prime factorization of [latex]115[/latex].
Solution
[latex]115 = 5 \times 23[/latex]
d. List all of the factors of [latex]115[/latex] in ascending order.
Solution
[latex]115: \{1, 115, 5, 23\}[/latex] are the pairs listed together
[latex]115: \{1, 5, 23, 115\}[/latex] are the factors listed in ascending order
e. Find the GCF([latex]92, 115[/latex]).
Solution
GCF([latex]92, 115) = 23[/latex]
We can go through a similar procedure to find the greatest common factor of three or more numbers. Below is an exercise in finding the GCF of three given numbers.
Exercise 6
Find the greatest common factor of [latex]48, 54[/latex] and [latex]63[/latex].
a. Find the prime factorization of [latex]48[/latex].
Solution
[latex]48 = 2 \times 2 \times 2 \times 2 \times 3[/latex]
b. List all of the factors of [latex]48[/latex] in ascending order.
Solution
[latex]48: \{1, 48, 2, 24, 3, 16, 4, 12, 6, 8\}[/latex] are the pairs listed together
[latex]48: \{1, 2, 3, 4, 6, 8, 12, 16, 24, 48\}[/latex] are the factors listed in ascending order
c. Find the prime factorization of [latex]54[/latex].
Solution
[latex]54 = 2 \times 3 \times 3 \times 3[/latex]
d. List all of the factors of [latex]54[/latex] in ascending order.
Solution
[latex]54: \{1, 54, 2, 27, 3, 18, 6, 9\}[/latex] are the pairs listed together
[latex]54: \{1, 2, 3, 6, 9, 18, 27, 54\}[/latex] are the factors listed in ascending order
e. Find the prime factorization of [latex]63[/latex].
Solution
[latex]63 = 3 \times 3 \times 7[/latex]
f. List all of the factors of [latex]63[/latex] in ascending order.
Solution
[latex]63: \{1, 63, 3, 21, 7, 9\}[/latex] are the pairs listed together
[latex]63: \{1, 3, 7, 9, 21, 63\}[/latex] are the factors listed in ascending order
g. Find the GCF([latex]48, 54, 63[/latex]).
Solution
GCF([latex]48, 54, 63) = 3[/latex]
As you might have realized, listing factors can still be a very time-consuming way to find the greatest common factor, especially if the numbers are very large or have a lot of factors.
It's time to get out your colored prime number squares and white composite number squares again. We'll be using these to prime factor sets of numbers, which can then be used to find the greatest common factor of a set of numbers. This method is usually faster than the one we just used.
Example 7 - Prime and Composite Number Squares Method
The goal of this next example is to find the greatest common factor of [latex]42[/latex] and [latex]72[/latex] using prime factorization with the prime and composite number squares.
Step 1: Use the squares to prime factor [latex]42[/latex] and [latex]72[/latex].
[latex]42 = 2 \times 3 \times 7[/latex] and [latex]72 = 2 \times 2 \times 2 \times 3 \times 3[/latex]
Step 2: Draw a line and put the prime factors of [latex]42[/latex] above it. Next to that, draw a line and put the prime factors of [latex]72[/latex] above it.
Step 3: Look at the prime factorization of the numbers. Move every factor they have in common under the line. They should have the same exact factors under the line, and they should have no common factors left above the line.
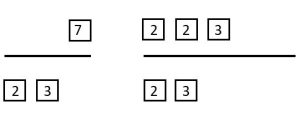
Step 4: The product of the factors under a line is the greatest common factor of the numbers. In this case, [latex]2 \times 3[/latex], or [latex]6[/latex], is the greatest common factor of [latex]42[/latex] and [latex]72[/latex].
Step 5: Use the correct notation to write the answer: GCF([latex]42, 72[/latex]) = [latex]6[/latex].
A similar process works for us to find the GCF of three numbers as shown in Example 8.
Example 8
This next example used the same steps to find the greatest common factor of [latex]16, 24[/latex] and [latex]36[/latex].
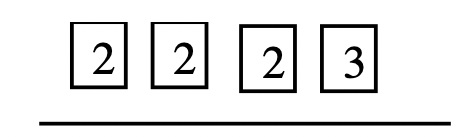
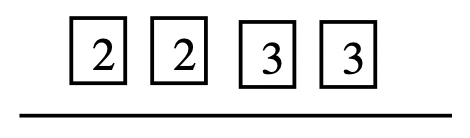
Step 1: Use the squares to prime factor [latex]16, 24[/latex] and [latex]36[/latex].
[latex]16 = 2 \times 2 \times 2 \times 2; 24 = 2 \times 2 \times 2 \times 3[/latex] and [latex]36 = 2 \times 2 \times 3 \times 3[/latex]
Step 2: Draw a line for each number and put the prime factors of each number above it.
 |
 |
 |
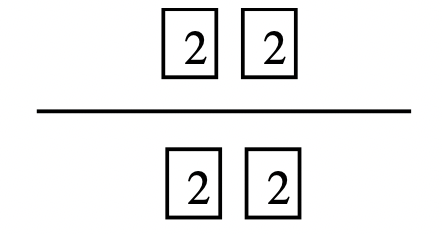
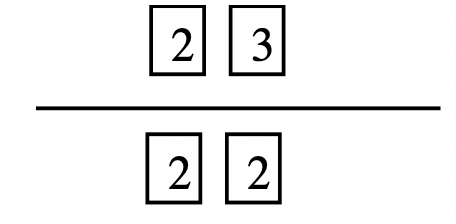
Step 3: Look at the prime factorization of the numbers. Move every factor that all three numbers have in common. There should be no factors left above the line that all three numbers have in common.
 |
 |
 |
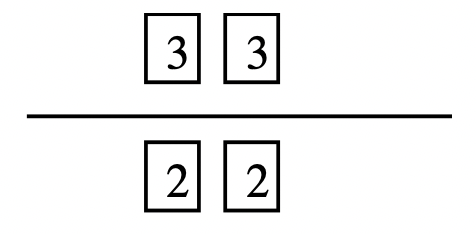Step 4: The product of the factors under a line is the greatest common factor of the numbers. In this case, [latex]2 \times 2[/latex], or [latex]4[/latex], is the greatest common factor of [latex]16, 24[/latex] and [latex]36[/latex].
Step 5: Use the correct notation to write the answer: GCF([latex]16, 24, 36[/latex]) = [latex]4[/latex].
Exercise 7
Use the steps shown in the previous two examples to find the greatest common factor of each problem. Show a picture of how the problem looks at step 3 where the prime factorization of the greatest common factor is shown under the line of each number you first prime factored.
a. [latex]GCF(42, 70)[/latex]
Solution
[latex]42 = 2 \times 3 \times 7[/latex]
[latex]70 = 2 \times 5 \times 7[/latex]
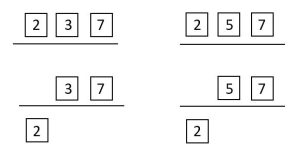
[latex]GCF(42, 70) = 2[/latex]
b. [latex]GCF(92, 115)[/latex]
Solution
[latex]92 = 2 \times 2 \times 23[/latex]
[latex]115 = 5 \times 23[/latex]
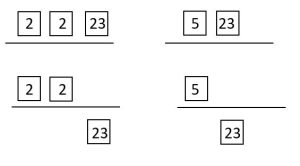
[latex]GCF(42, 70) = 23[/latex]
c. [latex]GCF(48, 54, 63)[/latex]
Solution
[latex]48 = 2 \times 2 \times 2 \times 2 \times 3[/latex]
[latex]54 = 2 \times 3 \times 3 \times 3[/latex]
[latex]63 = 3 \times 3 \times 7[/latex]
[latex]GCF(48, 54, 63) = 3[/latex]
d. [latex]GCF(306, 340)[/latex]
Solution
[latex]306 = 2 \times 3 \times 3 \times 17[/latex]
[latex]340 = 2 \times 2 \times 5 \times 17[/latex]
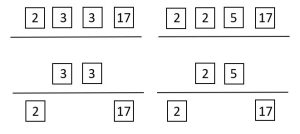
[latex]GCF(306, 340) = 2 \times 17 = 34[/latex]
e. [latex]GCF(125, 275, 400)[/latex]
Solution
[latex]125 = 5 \times 5 \times 5[/latex]
[latex]275 = 5 \times 5 \times 11[/latex]
[latex]400 = 2 \times 2 \times 2 \times 2 \times 5 \times 5[/latex]
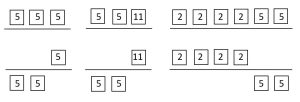
[latex]GCF(125, 275, 400) = 5 \times 5 = 25[/latex]
f. [latex]GCF(126, 168, 210)[/latex]
Solution
[latex]126 = 2 \times 3 \times 3 \times 7[/latex]
[latex]168 = 2 \times 2 \times 2 \times 3 \times 7[/latex]
[latex]210 = 2 \times 3 \times 5 \times 7[/latex]
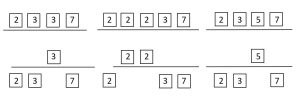
[latex]GCF(126, 168, 210)= 2 \times 3 \times 7 = 42[/latex]
This method, while useful, can be time-consuming. We can use the concept of prime numbers to find our GCF and streamline it to make it more efficient to work with. In the example below, we can develop this new method by using primes and their exponents to find our GCF.
Example 9
[latex]X[/latex], [latex]Y[/latex] and [latex]Z[/latex] are three large numbers that have been prime factored:
[latex]X = 2^{5} \times 3^{4} \times 7^{2} \times 11^{8} \times 13^{3}[/latex]
[latex]Y = 2^{4} \times 3^{5} \times 5^{3} \times 7^{7} \times 13^{2}[/latex]
[latex]Z = 2^{6} \times 3 \times 5^{5} \times 11^{3} \times 13^{4}[/latex]
Find the prime factorizations and write them using exponential notation for [latex]X[/latex], [latex]Y[/latex] and [latex]Z[/latex].
Solution:
Step 1: List the common prime factors (without exponents first) for [latex]X[/latex], [latex]Y[/latex] and [latex]Z[/latex].
The common prime factors that are in all three prime factorizations are [latex]2[/latex], [latex]3[/latex], and [latex]13[/latex].
Step 2: Determine how many of each prime factor are common to [latex]X[/latex], [latex]Y[/latex], and [latex]Z[/latex].
Since [latex]X[/latex] has [latex]5[/latex] factors of [latex]2[/latex], [latex]Y[/latex] has [latex]4[/latex] factors of [latex]2[/latex], and [latex]Z[/latex] has [latex]6[/latex] factors of [latex]2[/latex], they only have [latex]4[/latex] factors of [latex]2[/latex] in common. Similarly, they only have one factor of [latex]3[/latex] in common, and [latex]2[/latex] factors of [latex]13[/latex] in common.
Step 3: Make a conclusion by writing these exponents on the common prime factors to get the [latex]GCF[/latex] of the three numbers.
[latex]GCF(X, Y, Z) = 2^{4} \times 3 \times 13^{2}[/latex]
Did you notice that if you list the factors they have in common without exponents, you put on the smallest exponent they have in common for each prime?
Key Takeaways - Prime Factorization Method
For each value, list its prime factorization with exponents. To find the Greatest Common Factor (GCF) write down all the primes in common with the smallest exponents for each type of prime.
Write the prime factorization of the greatest common factor of the set of numbers. Assume each letter represents a different prime number in parts "c" and "d".
a. If [latex]X = 2^{4} \times 3^{2} \times 7^{6} \times 11^{3} \times 13^{2}[/latex] and [latex]Y = 2^{5} \times 3^{6} \times 5^{4} \times 7^{6} \times 13^{3}[/latex], then
[latex]GCF(X, Y) =[/latex]
Solution
[latex]GCF(X, Y) = 2^{4} \times 3^{2} \times 7^{6} \times 13^{2}[/latex]
b. If [latex]X = 3^{4} \times 5^{2} \times 7^{6}[/latex] and [latex]Y = 2^{5} \times 3^{6} \times 5^{6} \times 7^{3}[/latex] and [latex]Z = 2^{4} \times 3^{5} \times 5^{4}[/latex], then
[latex]GCF(X, Y, Z) =[/latex]
Solution
[latex]GCF(X, Y, Z) = 3^{4} \times 5^{2}[/latex]
c. If [latex]X = a^{4} \times b^{2} \times c^{6} \times d^{3} \times e^{2}[/latex] and [latex]Y = a^{5} \times c^{3} \times d^{4} \times e^{6} \times f^{3}[/latex], then
[latex]GCF(X, Y) =[/latex]
Solution
[latex]GCF(X, Y) = a^{4} \times c^{3} \times d^{3} \times e^{2}[/latex]
d. If [latex]X = a^{4} \times b \times c^{4} \times d^{3}[/latex] and [latex]Y = a^{5} \times b^{3} \times d^{4} \times e^{6}[/latex] and [latex]Z = a^{2} \times c^{3} \times d^{7} \times f^{3}[/latex], then
[latex]GCF(X, Y, Z) =[/latex]
Solution
[latex]GCF(X, Y, Z) = a^{2} \times d^{3}[/latex]
If two numbers have no factors in common, they are called relatively prime. In other words, if [latex]GCF(a, b) = 1[/latex], then [latex]a[/latex] and [latex]b[/latex] are relatively prime. The numbers, [latex]a[/latex] and [latex]b[/latex], might both be prime, both be composite, or one might be prime and the other composite. Two unequal primes are always relatively prime. For example, considering two primes [latex]3[/latex] and [latex]5[/latex], we have [latex]GCF(3, 5) = 1[/latex], so they are relatively prime. Generally speaking, if [latex]x[/latex] and [latex]y[/latex] are different prime numbers, then [latex]GCF(x, y) = 1[/latex], which means they are relatively prime. In general, one prime number and one composite number or two composite numbers might be relatively prime as well. For instance, although [latex]14[/latex] and [latex]15[/latex are both composite numbers, we have [latex]GCF(14, 15) = 1[/latex] because [latex]14 = 2 \times 7[/latex] and [latex]15 = 3 \times 5[/latex]. Therefore, [latex]14[/latex] and [latex]15[/latex] are relatively prime.
Exercise 9
a. Give an example of two composite numbers that are relatively prime. (answers will vary)
Solution
[latex]22[/latex] and [latex]35[/latex]
[latex]22 = 2 \times 11[/latex] and [latex]35 = 5 \times 7[/latex]
There are no primes in common.
b. Write a prime number and a composite number that are relatively prime. (answers will vary)
Solution
[latex]7[/latex] and [latex]22[/latex]
There are no primes in common since [latex]22 = 2 \times 11[/latex]
Further Exploration:
1. Assume [latex]GCF(28, x) = 1[/latex]. List all prime numbers that must not be factors of [latex]x[/latex]. Then give three examples (numbers) of what [latex]x[/latex] could equal.
2. If [latex]m[/latex] is a whole number, find the following:
a. [latex]GCF(2m, 3m) = \underline{\qquad\qquad}[/latex]
b. [latex]GCF (4m, 10m) = \underline{\qquad\qquad}[/latex]
c. [latex]GCF(m, m) = \underline{\qquad\qquad}[/latex]
d. [latex]GCF( m, 1) = \underline{\qquad\qquad}[/latex]
e. [latex]GCF(m, 0) = \underline{\qquad\qquad}[/latex]
The Old Chinese Method and The Euclidean Algorithm
Trying to find the greatest common factor of two large numbers by prime factorization is sometimes quite time-consuming. There are two other algorithms you can use that we'll use. One is called The Old Chinese Method, and the other is The Euclidean Algorithm. Both of these methods use a fact we can prove using what we know about divisibility, which says that the greatest common factor of two numbers is equal to the greatest common factor of the smaller number, and the difference of the original two numbers; i.e., if [latex]x\geq y[/latex], then [latex]GCF(x, y) = GCF(y, x – y)[/latex].
Prove the following statement: Let [latex]a\geq b[/latex]. If [latex]c|a[/latex] and [latex]c|b[/latex], then [latex]c|(a – b)[/latex].
Proof: If [latex]c|a[/latex], then [latex]cn = a[/latex] for some whole number, [latex]n[/latex]. If [latex]c|b[/latex], then [latex]cm = b[/latex] for some whole number, [latex]m[/latex]. Using these substitutions for [latex]a[/latex] and [latex]b[/latex], we get that [latex]a - b = cn - cm = c(n - m)[/latex], which shows [latex]c[/latex] is indeed a factor of [latex]a - b[/latex]. Therefore, [latex]c|(a – b)[/latex].
This theorem can be used to show that if [latex]a \geq b[/latex], then [latex]GCF(a, b) = GCF(b, a – b)[/latex]. The above theorem states that if [latex]c[/latex] is a factor of two numbers, then it is also a factor of their difference. Hence, if [latex]c[/latex] is a common factor of [latex]a[/latex] and [latex]b[/latex], where [latex]a \geq b[/latex], then [latex]c[/latex] is also a common factor of [latex]b[/latex] and [latex]a – b[/latex]. Since every common factor of [latex]a[/latex] and [latex]b[/latex] is also a common factor of [latex]ba[/latex] and [latex]a – b[/latex], the pairs [latex](a, b)[/latex] and [latex](b, a – b)[/latex] have the same common factors. So, [latex]GCF(a, b)[/latex] and [latex]GCF(b, a – b)[/latex] must also be the same number.
The Old Chinese Method employs the fact that [latex]GCF(a, b) = GCF(b, a – b)[/latex].
Note three more properties:
[latex]GCF(x, x) = x[/latex]: [latex]GCF(x, x)[/latex] states that the greatest common factor of the same two numbers is itself. That should be clear since [latex]x[/latex] is the greatest factor of each number, so each has [latex]x[/latex] as the greatest common factor.
[latex]GCF(x, 0) = x[/latex]: In this case, [latex]GCF(x, 0) = x[/latex], is true since every number is a factor of zero. So, since [latex]x[/latex] is the greatest factor of [latex]x[/latex], then [latex]x[/latex] is the greatest common factor of [latex]x[/latex] and [latex]0[/latex].
[latex]GCF(x, 1) = 1[/latex]: In this case, [latex]GCF(x, 1) = 1[/latex] is true since [latex]1[/latex] is a factor of every number, including [latex]x[/latex], and [latex]1[/latex] is the only factor of [latex]1[/latex]. Therefore, [latex]1[/latex] must be the greatest common factor of [latex]1[/latex] and [latex]x[/latex].
Old Chinese Method of finding the greatest common factor of two numbers:
Write the GCF of the two numbers in parentheses (remember the order of the numbers is irrelevant). Let that equal the GCF of the smaller of the two numbers, and the difference of the original two numbers. If the numbers in the parentheses are the same, that number is the GCF; if one of the new numbers is [latex]1[/latex], [latex]1[/latex] is the GCF. Otherwise, repeat the process until the two numbers are the same, or [latex]1[/latex] is one of the numbers. An example is shown below. On the right is an explanation of how we obtain the two new numbers in parentheses. The new numbers are underlined in the explanation.
Find [latex]GCF(546, 390)[/latex] using the Old Chinese Method.
Solution:
| [latex]GCF(546, 390)[/latex] | [latex]= GCF(390, 156)[/latex] | ([latex]\underline{390}[/latex] is smaller than [latex]546[/latex], [latex]546 - 390 = \underline{156}[/latex]) |
| [latex]= GCF(156, 234)[/latex] | ([latex]\underline{156}[/latex] is smaller than [latex]390[/latex], [latex]390 - 156 = \underline{234}[/latex]) | |
| [latex]= GCF(156, 78)[/latex] | ([latex]\underline{156}[/latex] is smaller than [latex]234[/latex], [latex]234 - 156 = \underline{78}[/latex]) | |
| [latex]= GCF(78, 78)[/latex] | ([latex]\underline{78}[/latex] is smaller than [latex]156[/latex], [latex]156 - 78 = \underline{78}[/latex]) | |
| [latex]= 78[/latex]
|
[latex]78[/latex] is the [latex]GCF(78, 78)[/latex]. The answer is the number!
|
Therefore, [latex]GCF(546, 390) = 78[/latex].
Check:
First, make sure [latex]78[/latex] is a factor of [latex]546[/latex] and [latex]390[/latex]: [latex]546 = 78\times 7[/latex] and [latex]390 = 78 \times 5[/latex]. Second, check to make sure the other factors of each ([latex]7[/latex] and [latex]5[/latex]) are relatively prime. If so, then [latex]78[/latex] is not only a factor of [latex]546[/latex] and [latex]390[/latex], but is in fact the greatest common factor of each since they have no other common factors (because [latex]7[/latex] and [latex]5[/latex] have no common factors).
Another example is shown below. On the right is an explanation of how we obtain the two new numbers (underlined) in parentheses. You do not need to write that out.
Find [latex]GCF(1200, 504)[/latex] using the Old Chinese Method.
Solution:
| [latex]GCF(1200, 504)[/latex] | [latex]= GCF(504, 696)[/latex] | ([latex]\underline{504}[/latex] is smaller than [latex]1200[/latex], [latex]1200 - 504 = \underline{696}[/latex]) |
| [latex]= GCF(504, 192)[/latex] | ([latex]\underline{504}[/latex] is smaller than [latex]696[/latex], [latex]696 - 504 = \underline{192}[/latex]) | |
| [latex]= GCF(192, 312)[/latex] | ([latex]\underline{192}[/latex] is smaller than [latex]504[/latex], [latex]504 - 192 = \underline{312}[/latex]) | |
| [latex]= GCF(192, 120)[/latex] | ([latex]\underline{192}[/latex] is smaller than [latex]312[/latex], [latex]312 - 192 = \underline{120}[/latex]) | |
| [latex]= GCF(120, 72)[/latex] | ([latex]\underline{120}[/latex] is smaller than [latex]192[/latex], [latex]192 - 120 = \underline{72}[/latex]) | |
| [latex]= GCF(72, 48)[/latex] | ([latex]\underline{72}[/latex] is smaller than [latex]120[/latex], [latex]120 - 72 = \underline{48}[/latex]) | |
| [latex]= GCF(48, 24)[/latex] | ([latex]\underline{48}[/latex] is smaller than [latex]72[/latex], [latex]72 - 48 = \underline{24}[/latex]) | |
| [latex]= GCF(24, 24)[/latex] | ([latex]\underline{24}[/latex] is smaller than [latex]48[/latex], [latex]48 - 24 = \underline{24}[/latex]) | |
| [latex]= 24[/latex]
|
[latex]24[/latex] is the [latex]GCF(24, 24)[/latex]. The answer is the number!
|
Therefore, [latex]GCF(1200, 504) = 24[/latex].
Check:
First, make sure [latex]24[/latex] is a factor of [latex]1200[/latex] and [latex]504[/latex]: [latex]1200 = 24 \times 50[/latex] and [latex]504 = 24 \times 21[/latex]. Second, check to make sure the other factors of each ([latex]25[/latex] and [latex]21[/latex]) are relatively prime. If so, then [latex]24[/latex] is not only a factor of [latex]1200[/latex] and [latex]504[/latex], but is in fact the greatest common factor of each since they have no other common factors (because [latex]25[/latex] and [latex]21[/latex] have no common factors.)
Here is one more example without the explanation on its right side. This is how we write out the solution when we use the Old Chinese Method to find the greatest common factor of two numbers.
Find [latex]GCF(667, 437)[/latex] using the Old Chinese Method.
Solution:
| [latex]GCF(667, 437)[/latex] | [latex]= GCF(437, 230)[/latex] | [latex]667 - 437 = 230[/latex] |
| [latex]= GCF(230, 207)[/latex] | [latex]437 - 230 = 207[/latex] | |
| [latex]= GCF(207, 23)[/latex] | [latex]230 - 207 = 23[/latex] | |
| [latex]= GCF(23, 184)[/latex] | [latex]207 - 23 = 184[/latex] | |
| [latex]= GCF(23, 161)[/latex] | [latex]184 - 23 = 161[/latex] | |
| [latex]= GCF(23, 138)[/latex] | [latex]171 - 23 = 138[/latex] | |
| [latex]= GCF(23, 115)[/latex] | [latex]138 - 23 = 115[/latex] | |
| [latex]= GCF(23, 92)[/latex] | [latex]115 - 23 = 92[/latex] | |
| [latex]= GCF(23, 69)[/latex] | [latex]92 - 23 = 69[/latex] | |
| [latex]= GCF(23, 46)[/latex] | [latex]69 - 23 = 46[/latex] | |
| [latex]= GCF(23, 23)[/latex] | [latex]46 - 23 = 23[/latex] | |
| [latex]= 23[/latex] | Remember: The answer is the number! |
Therefore, [latex]GCF(667, 437) = 23[/latex].
Check:
First, make sure [latex]23[/latex] is a factor of [latex]667[/latex] and [latex]437[/latex]: [latex]667 = 23 \times 29[/latex] and [latex]437 = 23 \times 19[/latex]. Second, check to make sure the other factors of each ([latex]29[/latex] and [latex]19[/latex]) are relatively prime. If so, then [latex]23[/latex] is not only a factor of [latex]667[/latex] and [latex]437[/latex], but is in fact the greatest common factor of each since they have no other common factors (because [latex]29[/latex] and [latex]19[/latex] have no common factors.)
A comment: You could have obtained the greatest common factor of the previous three examples by prime factoring. Often, this is a lengthy process for large numbers that look like they might be prime, as in the last example. Therefore, the Old Chinese provides an alternative way to obtain the greatest common factor. After doing a few exercises using this method, we'll explore another alternate method, called the Euclidean Algorithm, which is related to, but usually takes less steps than, the Old Chinese Method.
Exercise 10
Use the Old Chinese Method to compute the greatest common factor of the numbers given. Use correct notation, and show each step. State the answer. Then, show how you check your answer. Use the previous example as a model to do these problems.
a.
| [latex]GCF(143, 91)[/latex] | [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | Show the check here: |
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]=\underline{\qquad}[/latex] |
Solution
| [latex]GCF(143, 91)[/latex] | [latex]= GCF (91, 52)[/latex] | [latex]143 - 91 = 52[/latex] |
| [latex]= GCF (52, 39)[/latex] | [latex]91 - 52 = 39[/latex] | |
| [latex]= GCF (39, 13)[/latex] | [latex]52 - 39 = 13[/latex] | |
| [latex]= GCF (13, 26)[/latex] | [latex]39 - 13 = 26[/latex] | |
| [latex]= GCF (13, 13)[/latex] | [latex]26 - 13 = 13[/latex] | |
| [latex]= 13[/latex] |
b.
| [latex]GCF(468, 378)[/latex] | [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | Show the check here: |
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]=\underline{\qquad}[/latex] |
Solution
| [latex]GCF(468, 378)[/latex] | [latex]= GCF (378, 90)[/latex] | [latex]468 - 378 = 90[/latex] |
| [latex]= GCF (90, 288)[/latex] | [latex]378 - 90 = 288[/latex] | |
| [latex]= GCF (90, 198)[/latex] | [latex]288 - 90 = 198[/latex] | |
| [latex]= GCF (90, 108)[/latex] | [latex]198 - 90 = 108[/latex] | |
| [latex]= GCF (90, 18)[/latex] | [latex]108 - 90 = 18[/latex] | |
| [latex]= GCF (18, 72)[/latex] | [latex]90 - 18 = 72[/latex] | |
| [latex]= GCF (18, 54)[/latex] | [latex]72 - 18 = 54[/latex] | |
| [latex]= GCF (18, 36)[/latex] | [latex]54 - 18 = 36[/latex] | |
| [latex]= GCF (18, 18)[/latex] | [latex]36 - 18 = 18[/latex] | |
| [latex]= 18[/latex] |
c.
| [latex]GCF(504, 180)[/latex] | [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | Show the check here: |
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]=\underline{\qquad}[/latex] | ||
Solution
| [latex]GCF(504, 180)[/latex] | [latex]= GCF (180, 324)[/latex] | [latex]504 - 180 = 324[/latex] |
| [latex]= GCF (180, 144)[/latex] | [latex]324 - 180 = 144[/latex] | |
| [latex]= GCF (144, 36)[/latex] | [latex]180 - 144 = 36[/latex] | |
| [latex]= GCF (36, 108)[/latex] | [latex]144 - 36 = 108[/latex] | |
| [latex]= GCF (36, 72)[/latex] | [latex]108 - 36 = 72[/latex] | |
| [latex]= GCF (36, 36)[/latex] | [latex]72 - 36 = 36[/latex] | |
| [latex]=36[/latex] | ||
Using the Old Chinese Method could be quite tedious. Take a further look at the solution in Example 11:
| [latex]GCF(1200, 504)[/latex] | [latex]= GCF(504, 696)[/latex] | ([latex]\underline{504}[/latex]is smaller than [latex]1200[/latex], [latex]\underline{696} = 1200 – 504[/latex]) |
| [latex]= GCF(504, 192)[/latex] | ([latex]\underline{504}[/latex] is smaller than [latex]696[/latex], [latex]\underline{192} = 696 – 504[/latex]) | |
| [latex]= GCF(192, 312)[/latex] | ([latex]\underline{192}[/latex] is smaller than [latex]504[/latex], [latex]\underline{312} = 504 – 192[/latex]) | |
| [latex]= GCF(192, 120)[/latex] | ([latex]\underline{192}[/latex] is smaller than [latex]312[/latex], [latex]\underline{120} = 312 – 192[/latex]) | |
| [latex]= GCF(120, 72)[/latex] | ([latex]\underline{120}[/latex] is smaller than [latex]192[/latex], [latex]\underline{72} = 192 – 120[/latex]) | |
| [latex]= GCF(72, 48)[/latex] | ([latex]\underline{72}[/latex] is smaller than [latex]120[/latex], [latex]\underline{48} = 120 – 72[/latex]) | |
| [latex]= GCF(48, 24)[/latex] | ([latex]\underline{48}[/latex] is smaller than [latex]72[/latex], [latex]\underline{24} = 72 – 48[/latex]) | |
| [latex]= GCF(24, 24)[/latex] | ([latex]\underline{24}[/latex] is smaller than [latex]48[/latex], [latex]\underline{24} = 72-48[/latex]) | |
| [latex]= 24[/latex]
|
[latex]24[/latex] is the [latex]GCF(24, 24)[/latex]. The answer is a number!
|
In the beginning of this example, [latex]GCF(1200, 504)[/latex], we had to subtract [latex]504[/latex] twice until we got [latex]GCF(504, 192)[/latex]. Then, notice once we wrote [latex]GCF(504, 192)[/latex], we had to subtract [latex]192[/latex] twice until we got [latex]GCF(192, 120)[/latex]. Basically, we do repeated subtraction until we get a number smaller than the one we are subtracting. Repeated subtraction is actually division. Note that [latex]1200 \div 504 = 2[/latex] remainder [latex]192[/latex]. On the second step, we see [latex]GCF(504, 192)[/latex], which has the smaller of the numbers in the original parentheses ([latex]504[/latex]), and the remainder after dividing the larger number ([latex]1200[/latex]) by the smaller number ([latex]504[/latex]). Note that [latex]504 \div 192 = 2[/latex] remainder [latex]120[/latex]. Look at the fourth step: we see [latex]GCF(192, 120)[/latex], which has the smaller of the numbers in [latex]GCF(504, 192)[/latex], and the remainder after dividing the larger number ([latex]504[/latex]) by the smaller number ([latex]192[/latex]). The Euclidean Algorithm uses division instead of repeated subtraction to shorten the steps.
How to use the Euclidean Algorithm to find the greatest common factor of two numbers:
Write the GCF of the two numbers in parentheses (remember the order of the numbers is irrelevant). The smaller of the two numbers will be one of the numbers in the next parentheses. To get the other number, divide the larger number by the smaller number, and put the remainder in parentheses. If the smaller number is a factor of the larger number, that means it will divide evenly, so there will be no remainder. That means the remainder is [latex]0[/latex]. Remember to put the remainder in the parentheses, not the quotient! If one of the new numbers in the parentheses is zero, the other number is the GCF; if one of the new numbers is [latex]1[/latex], then [latex]1[/latex] is the GCF. Otherwise, repeat the process until one of the two numbers is [latex]0[/latex] or [latex]1[/latex]. An example is shown below. This is the first example we did using the Old Chinese Method. You might want to look back and compare. On the right is an explanation of how I obtained the two new numbers in parentheses.
Use the Euclidean Algorithm to find [latex]GCF(546, 390)[/latex].
| [latex]GCF(546, 390)[/latex] | = [latex]GCF(390, 156)[/latex] | ([latex]546 \div 390 = 1 r 156[/latex]) |
| = [latex]GCF(156, 78)[/latex] | ( [latex]390 \div 156 = 2 r 78[/latex]) | |
| = [latex]GCF(78, 0)[/latex] | ( [latex]156 \div 78 = 2 r 0[/latex]) | |
| = [latex]78[/latex] | The answer is a number! | |
Therefore, [latex]GCF(546, 390) = 78[/latex]
Check:
First, make sure [latex]78[/latex] is a factor of [latex]546[/latex] and [latex]390[/latex]: [latex]546 = 78 = \times 7[/latex] and [latex]390 = 78 \times 5[/latex]. Second, check to make sure the other factors of each ([latex]7[/latex] and [latex]5[/latex]) are relatively prime. If so, then [latex]78[/latex] is not only a factor of [latex]546[/latex] and [latex]390[/latex], but is in fact the greatest common factor of each since they have no other common factors (because [latex]7[/latex] and [latex]5[/latex] have no common factors).
Below is another example – we did this earlier using the Old Chinese Method. Let's compare methods to see if we can get the same answer.
Use the Euclidean Algorithm to find [latex]GCF(667, 437)[/latex].
| [latex]GCF(667, 437)[/latex] | = [latex]GCF(437, 230)[/latex] | ([latex]667 \div 437 = 1 r 230[/latex]) |
| = [latex]GCF(230, 207)[/latex] | ([latex]437 \div 230 = 1 r 207[/latex]) | |
| = [latex]GCF(207, 23)[/latex] | ([latex]230 \div 207 = 1 r 23[/latex]) | |
| = [latex]GCF(23, 0)[/latex] | ([latex]207 \div 23 = 9 r 0[/latex]) | |
| = [latex]23[/latex] | The answer is a number! | |
Therefore, [latex]GCF(667, 437) = 23[/latex]
Check:
First, make sure [latex]23[/latex] is a factor of [latex]667[/latex] and [latex]437[/latex]: [latex]667 = 23 \times 29[/latex] and [latex]437 = 23 \times 19[/latex]. Second, check to make sure the other factors of each ([latex]29[/latex] and [latex]19[/latex]) are relatively prime. If so, then [latex]23[/latex] is not only a factor of [latex]667[/latex] and [latex]437[/latex], but is in fact the greatest common factor of each since they have no other common factors (because [latex]29[/latex] and [latex]19[/latex] have no common factors.)
Teaching Tip - Euclidean Algorithm Method
The most common mistake people make when using the Euclidean Algorithm is on the last step when the smaller number divides evenly into the larger number. This means that the remainder is [latex]0[/latex]. It doesn't matter what the quotient is, it's the remainder that matters. This [latex]0[/latex] goes into the parentheses.
Also, zero is not a factor of any number except zero, so the GCF can't be zero. On the other hand, every number is a factor of zero. So, when zero is one of the numbers in parentheses, the other number is the GCF. Remember to always check your answer!!!
Use the Euclidean Algorithm to compute the greatest common factor of the numbers given. Use correct notation, and show each step. State the answer. Then, show how you check your answer. Use the previous example as a model to do these problems. These are the same exercises you did using the Old Chinese Method in exercise 27. You might want to compare the two methods when you are done. Of course, the answer should be the same.
a.
| [latex]GCF(143, 91)[/latex] | [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | Show the check here: |
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]=\underline{\qquad}[/latex] |
Solution
| [latex]GCF(143, 91)[/latex] | [latex]= GCF (91, 52)[/latex] | [latex]143 \div 91 = 1 r 52[/latex] |
| [latex]= GCF (52, 39)[/latex] | [latex]91 \div 52 = 1 r 39[/latex] | |
| [latex]= GCF (39, 13)[/latex] | [latex]52 \div 39 = 1 r 13[/latex] | |
| [latex]= GCF (13, 0)[/latex] | [latex]39 \div 13 = 3 r 0[/latex] | |
| [latex]= 13[/latex] |
b.
| [latex]GCF(468, 378)[/latex] | [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | Show the check here: |
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]=\underline{\qquad}[/latex] |
Solution
| [latex]GCF(468, 378)[/latex] | [latex]= GCF (378, 90)[/latex] | [latex]468 \div 378 = 1 r 90[/latex] |
| [latex]= GCF (90, 18)[/latex] | [latex]378 \div 90 = 4 r 18[/latex] | |
| [latex]= GCF (18, 0)[/latex] | [latex]90 \div 18 = 5 r 0[/latex] | |
| [latex]= 18[/latex] |
c.
| [latex]GCF(504, 180)[/latex] | [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | Show the check here: |
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]= GCF (\underline{\qquad},\underline{\qquad} )[/latex] | ||
| [latex]=\underline{\qquad}[/latex] |
Solution
| [latex]GCF(504, 180)[/latex] | [latex]= GCF (18, 144)[/latex] | [latex]504 \div 180 = 2 r 144[/latex] |
| [latex]= GCF (144, 36)[/latex] | [latex]180 \div 144 = 1 r 36[/latex] | |
| [latex]= GCF (36, 0)[/latex] | [latex]144 \div 36 = 4 r 0[/latex] | |
| [latex]= 36[/latex] |
Now we have learned three ways to find the greatest common factor of two numbers: (i) by prime factoring, (ii) the Old Chinese Method, or (iii) the Euclidean Algorithm.
Exercise 12
For each pair of numbers, find the greatest common factor i) by prime factorization, ii) by the Old Chinese Method, and c) by the Euclidean Algorithm. After you write the answer, iii) show how to check the answer.
a. Find [latex]GCF(418, 88)[/latex].
Solution
i) Prime Factorization
[latex]418 = 2 \times 11 \times 19[/latex]
[latex]88 = 2^{3} \times 11[/latex]
The [latex]GCF(418, 88) = 2 \times 11 = 22[/latex]
ii) Old Chinese Method
| [latex]GCF(418, 88)[/latex] | [latex]= GCF(88, 330)[/latex] | [latex]418 – 88 = 330[/latex] |
| [latex]= GCF(88, 242)[/latex] | [latex]330 - 88 = 242[/latex] | |
| [latex]= GCF(88, 154)[/latex] | [latex]242 - 88 = 154[/latex] | |
| [latex]= GCF(88, 66)[/latex] | [latex]154 - 88 = 66[/latex] | |
| [latex]= GCF(66, 22)[/latex] | [latex]88 - 66 = 22[/latex] | |
| [latex]= GCF(22, 44)[/latex] | [latex]66 - 22 = 44[/latex] | |
| [latex]= GCF(22, 22)[/latex] | [latex]44 - 22 = 22[/latex] | |
| [latex]= 24[/latex] | The answer is a number! | |
iii) Euclidean Algorithm
| [latex]GCF(418, 88)[/latex] | [latex]= GCF(88, 66)[/latex] | [latex]418 \div 88 = 4 r 66[/latex] |
| [latex]= GCF(66, 22)[/latex] | [latex]88 \div 66 = 1 r 22[/latex] | |
| [latex]= GCF(22, 0)[/latex] | [latex]66 \div 22 = 3 r 0[/latex] | |
| [latex]= 22[/latex] |
b. Find [latex]GCF(527, 465)[/latex].
Solution
i) Prime Factorization
[latex]529 = 17 \times 31[/latex]
[latex]465 = 3 \times 5 \times 31[/latex]
[latex]GCF(527, 465) = 31[/latex]
ii) Old Chinese Method
| [latex]GCF(527, 465)[/latex] | [latex]= GCF(465, 62)[/latex] | [latex]527 - 465 = 62[/latex] |
| [latex]= GCF(62, 403)[/latex] | [latex]465 - 62 = 403[/latex] | |
| [latex]= GCF(62 , 341)[/latex] | [latex]403- 62 = 341[/latex] | |
| [latex]= GCF(62 , 279)[/latex] | [latex]341 - 62 = 279[/latex] | |
| [latex]= GCF(62, 217)[/latex] | [latex]279 - 62 = 217[/latex] | |
| [latex]= GCF(62, 155)[/latex] | [latex]271 - 62 = 155[/latex] | |
| [latex]= GCF(62, 93)[/latex] | [latex]155 - 62 = 93[/latex] | |
| [latex]= GCF(62, 31)[/latex] | [latex]93 - 62 = 31[/latex] | |
| [latex]= GCF(31, 31)[/latex] | [latex]62 - 31 = 31[/latex] | |
| [latex]= 31[/latex] | The answer is a number! |
iii) Euclidean Algorithm
| [latex]GCF(527, 465)[/latex] | [latex]= GCF (465, 62)[/latex] | [latex]527 \div 465 = 1 r 62[/latex] |
| [latex]= GCF (62, 31)[/latex] | [latex]465 \div 62 = 7 r 31[/latex] | |
| [latex]= GCF (31, 0)[/latex] | [latex]62 \div 31 = 2 r 0[/latex] | |
| [latex]= 31[/latex] |
c. Find [latex]GCF(353, 213)[/latex].
Solution
i) Prime Factorization
[latex]353[/latex] is prime.
[latex]213 = 3 \times 71[/latex]
[latex]GCF(353, 213) = 1[/latex]
ii) Old Chinese Method
| [latex]GCF(353, 213)[/latex] | [latex]= GCF(213, 140)[/latex] | [latex]353 - 213 = 140[/latex] | |||
| [latex]= GCF(140, 73)[/latex] | [latex]213 - 140 = 73[/latex] | ||||
| [latex]= GCF(73, 67)[/latex] | [latex]140 - 73 = 67[/latex] | ||||
| [latex]= GCF(67, 6)[/latex] | [latex]73 - 67 = 6[/latex] | ||||
| [latex]= GCF(6, 61)[/latex] | [latex]67 - 6 = 61[/latex] | ||||
| [latex]= GCF(6, 55)[/latex] | [latex]61 - 6 = 55[/latex] | ||||
| [latex]= GCF(6, 49)[/latex] | [latex]55 - 6 = 49[/latex] | ||||
| [latex]= GCF(6, 43)[/latex] | [latex]49 - 6 = 43[/latex] | ||||
| [latex]= GCF(6, 37)[/latex] | [latex]43 - 6 = 37[/latex] | ||||
| [latex]= GCF(6, 31)[/latex] | [latex]37 - 6 = 31[/latex] | ||||
| [latex]= GCF(6, 25)[/latex] | [latex]31 - 6 = 25[/latex] | ||||
| [latex]= GCF(6, 19)[/latex] | [latex]25 - 6 = 19[/latex] | ||||
| [latex]= GCF(6, 13)[/latex] | [latex]19 - 6 = 13[/latex] | ||||
| [latex]= GCF(6, 7)[/latex] | [latex]13 - 6 = 7[/latex] | ||||
| [latex]= GCF(6, 1)[/latex] | [latex]7 - 6 = 1[/latex] | ||||
| [latex]= 1[/latex] | The answer is 1 since the numbers are relatively prime. | ||||
iii) Euclidean Algorithm
| [latex]GCF(353, 213)[/latex] | = [latex]GCF(213, 140)[/latex] | [latex]353 \div 213 = 1 r 140[/latex] |
| = [latex]GCF(140, 73)[/latex] | [latex]213 \div 140 = 1 r 73[/latex] | |
| = [latex]GCF(73, 67)[/latex] | [latex]140 \div 73 = 1 r 67[/latex] | |
| = [latex]GCF(67, 6)[/latex] | [latex]73 \div 67 = 1 r 6[/latex] | |
| = [latex]GCF(6, 1)[/latex] | [latex]67 \div 6 = 11 r 1[/latex] | |
| = [latex]1[/latex] | The answer is 1 since the numbers are relatively prime. | |