28 Module 5.1 The Meaning of Division
Louisiana Student Standards
Standard Number |
Description of Standard |
| 3.OA.2 | Interpret whole-number quotients of whole numbers, e.g., interpret [latex]56 \div 8[/latex] as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 objects each. For example, describe a context in which a number of shares or a number of groups can be expressed as [latex]56\div 8[/latex]. |
| 3.OA.3 | Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem. |
| 3.OA.4 | Determine the unknown whole number in a multiplication or division equation relating three whole numbers. For example, determine the unknown number that makes the equation true in each of the equations 8 [latex]\times[/latex] ? = 48, 5 [latex]=\Box\div[/latex] 3, 6 [latex]\times[/latex] 6 = ?. |
| 3.OA.5 | Understand division as an unknown-factor problem. For example, find 32 [latex]\div[/latex]8 by finding the number that makes 32 when multiplied by 8. |
| 4.NBT.6 | Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models. |
| 5.NBT.6 | Find whole-number quotients of whole numbers with up to four-digit dividends and two-digit divisors, using strategies based on place value, the properties of operations, subtracting multiples of the divisor, and/or the relationship between multiplication and division. Illustrate and/or explain the calculation by using equations, rectangular arrays, area models, or other strategies based on place value. |
You will need: Centimeter Strips (Material Cards 16A-16L) and Base Blocks (Material Cards 3 - 15)
There are many ways to view division and it depends on the situation as to which visualization is the most useful. For example, if you have 20 students in your class and want to split them into 4 groups, it is different from wanting to split them into groups of size 4. But, both situations show that 20 divided by 4 equals 5. It’s important for students to be comfortable with both visualizations for success in their later mathematics. Let’s dive into these two methods.
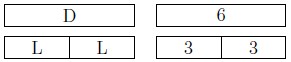
In this activity, we will divide H by Y, which we write as [latex]H \div Y[/latex]. First, lay out one hot pink c-strip (H). Separately, line up yellow c-strips (Y) one-by-one until you have come as close as possible to matching the hot pink c-strip without being longer than it. You know you are done if adding one more yellow c-strip makes the train longer than the hot pink c-strip.
a. How many yellow c-strips did you use?
Solution
Two yellow c-strips.
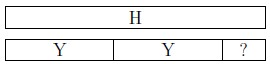
b.
This piece, which must be shorter than the divisor, is called the REMAINDER.
Put the hot pink strip next to the train you formed. It should look like this:

What did we just do? We took our first number (H) and subtracted the second number (Y) over and over until we could not subtract anymore without getting a negative number. Then, we figured out how much of H was leftover.
We have just visually represented [latex]H \div Y[/latex].
Definition - Dividend, Divisor, Quotient, Remainder
Consider the division problem [latex]H \div Y[/latex].
- The part before the division sign, H, is called the dividend.
- The part after the division sign, Y, is called the divisor.
If H and Y are whole numbers with [latex]Y \leq H[/latex]
- The quotient is the maximum number of times the divisor can be subtracted from the dividend without resulting in a negative number.
- The remainder is the difference between the dividend and the product of the quotient and divisor.
Teaching tip: Avoid using phrases like “the dividend is the larger number and the divisor is the smaller number” or “big divided by small.” This is not true as students advance in mathematics and need to compute things like ¼ ÷ 5.
To compute [latex]H \div Y[/latex], we need to figure out what goes in the blanks to make the equation in part c, below, true. The first blank will contain the number of yellow c-strips used, and the second blank is the length of the c-strip used for the remainder. We made a train of yellows, with at most one extra piece to form the length of H. Notice this is a train of yellows (which can be formed into a rectangle) plus an extra piece. Form the two yellow strips into a rectangle and find the c-strip that goes across the width. That c-strip goes in the first blank, and the extra piece (R) goes in the second blank. Fill in the blanks of the equation below. This equation should make sense by looking at the picture above showing H and the train are the same length.
c.
We can now conclude that: [latex]H \div Y[/latex] = [latex]\mathbf{Q}[/latex] remainder [latex]\underline{R}[/latex], since [latex]H = \mathbf{Q} \cdot Y[/latex] + [latex]\underline{R}[/latex]. To help you distinguish between them, the QUOTIENT is in bold, and the REMAINDER is underlined. This can be written as a statement about numbers by translating each c-strip to a number given by the strip's length.
Writing in the value of our strips, our picture transforms into the following.

Using numbers in the above equation, [latex]12 \div 5[/latex] = [latex]\mathbf{2}[/latex] remainder [latex]\underline{2}[/latex], since 12 = [latex]\mathbf{2} \cdot 5[/latex] + [latex]\underline{2}[/latex]
Classroom Connection: You ask students to represent [latex]29\div4[/latex] and one of them draws the following picture. What is their mistake?

Solution
The remainder, 5, is larger than the divisor, 4. The student stopped subtracting 4's too soon. They should have used one more piece of length 4 before figuring out the remainder.
Exercise 1
For a - e, do the division using the c-strips to make a train of as many of the divisor as possible such that the length of the train you make is less than or equal to the length of the dividend, and if you were to add one more of the divisor to the train, it would be longer than the dividend. If the train ends up being the same length as the dividend, there will be no remainder and the second blank will be zero. Draw a diagram showing the c-strip that is the dividend and under it, draw the train you formed. Do this the same way we did it for the exploration activity. Follow the example below.
[latex]H \div Y[/latex] = [latex]\mathbf{2}[/latex] remainder [latex]\underline{2}[/latex], since H = [latex]\mathbf{2}[/latex] [latex]\cdot[/latex] Y + [latex]\underline{2}[/latex]
[latex]12 \div 5[/latex] = [latex]\mathbf{2}[/latex] remainder [latex]\underline{2}[/latex], since 12 = [latex]\mathbf{2}[/latex] [latex]\cdot[/latex] 5 + [latex]\underline{2}[/latex]
Show diagram below:

Solution(Diagrams)
A lot of elementary school curricula introduce division through base blocks. The blocks are used to visually represent the division problem. Get out your base blocks and let's explore division, like your future students might do.
Exercise 2
Count out 36 unit blocks. How would you divide the 36 blocks by 2? Explain how you would do it, and show a picture of what you did. What is the answer?
(Pictures will vary.)
Exercise 3
Get out your base four blocks now, and trade in 36 units for a number in base four.
a. Write 36 as a base four numeral.
Solution
[latex]210_{\text{four}}[/latex]
b. Decide how to divide this by 2 using base four blocks. Explain how you would do it, and show a picture of what you did.
(Pictures will vary)
c. What is the answer in base four?
Solution
[latex]102_{\text{four}}[/latex]
d. Write the division problem and the quotient (answer) in base four: [latex]\underline{\qquad} \div 2_{\text{four}} = \underline{\qquad}[/latex]
Solution
[latex]210_{\text{four}} \div 2_{\text{four}} = 102_{\text{four}}[/latex]
Notice that 18 is the same as [latex]102_{\text{four}}[/latex]. This makes sense because both [latex]36\div 2[/latex] and [latex]210_{\text{four}} \div 2_{\text{four}}[/latex] represent the exact same question in two different forms.
Exercise 4
Get out your base three blocks now, and trade in 36 units for a number in base three.
a. Write 36 as a base three numeral.
Solution
[latex]1100_{\text{three}}[/latex]
b. Decide how to divide this by 2 using base three blocks. Explain how you would do it, and show a picture of what you did.
(Pictures will vary)
c. What is the answer in base three?
Solution
[latex]200_{\text{three}}[/latex]
d. Write the division problem and the quotient (answer) in base three: [latex]\underline{\qquad} \div 2_{\text{three}} = \underline{\qquad}[/latex]
Solution
[latex]1100_{\text{three}} \div 2_{\text{three}} = 200_{\text{three}}[/latex]
Exercise 5
Count out 48 unit blocks. How would you divide the 48 blocks by 16? Explain how you would do it, and show a picture of what you did. What is the answer?
(Pictures will vary.)
Exercise 6

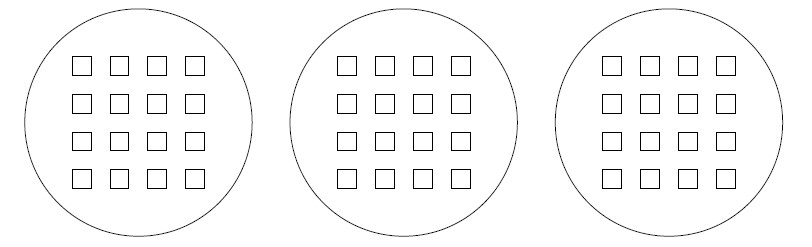
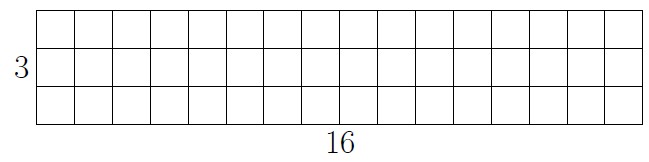
Solution
All three pictures are correct. The first two show three groups of size 16. The third shows both 3 groups of size 16 and 16 groups of size 3 depending on if you look at rows or columns.
Note that there are other possible pictures, such as 16 circles, each with 3 blocks inside.
Based on Exercise 6, we see that there are multiple ways of thinking about and visualizing division. The two word problems below both describe the division [latex]18\div 3[/latex], but the problems are really quite different.
Word Problem A:
If you have 18 cookies and want to divide the cookies up equally among your three children, how many cookies should you give to each child?
Word Problem B:
If you have 18 cookies and want to make baggies having three cookies in each to put in lunch boxes, how many baggies will you be able to make?
Both require the division problem [latex]18 \div 3[/latex], and the answer to each problem is 6. But the picture used to solve each is very different.
In Word Problem A, you are told how many kids there are, and you are asked to figure out how many cookies each child should be given. Imagine 3 children in front of you. You need to disburse the cookies amongst the 3 children so that each receives the same number of cookies. To begin, you might draw a model to represent three kids. It might look something like this:
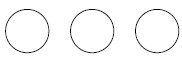
You know there are 3 kids and each will be given the same number of cookies so that the total number of cookies they all have is 18. After disbursing, you might show the picture like this:
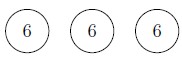
This is a way to illustrate that each of the 3 children has 6 cookies. If you prefer, you can actually draw 6 dots or 6 cookies in each circle. It's up to you.
Note that if you look at the model drawn, it is simply the multiplication problem [latex]3\cdot 6[/latex], since there are 3 sets/groups of 6 added together. The model of division Word Problem A represents is called:
Partitioning into (Equal) Subsets Model of Division
In this model, the divisor is the number of subsets/groups in which to disburse something. The dividend, 18, must be divided amongst 3 equal subsets (3 is the divisor). The quotient (answer to the division problem) will be the number of elements (6) placed in each subset (the kids, in this case.) The task is to partition 18 cookies into 3 equal subsets. In this model, you are given how many subsets there are (from reading the problem in this case, each kid represents one subset), but you do not how many are in each subset. (That is the question being asked in this case, how many cookies each child should receive.) You do the division to figure out how many elements will end up in each subset. After doing the division, the number of elements IN each subset is the answer to the problem.
One way to distinguish that a problem is suggesting this model is to consider whether the information in the problem provides you with the number of subsets. If it does, as in Word Problem A, then it is the partitioning into equal subsets model.
Okay, let's look at Word Problem B now.
If you have 18 cookies and want to make baggies having three cookies in each to later put in lunch boxes, how many baggies will you be able to make?
In Word Problem B, you don’t know how many subsets there will be. In fact, you are being asked how many subsets you will be able to make, so the partitioning into subsets interpretation wouldn't apply.
What you do know is how many of something will be in each subset. You would place three cookies in a baggie, then 3 more in another baggie, and so on. You won’t know how many subsets you will have until you finish disbursing the cookies. You would take three cookies away at a time and put them in a baggie, until you ran out of cookies. After doing this, a picture you might draw to illustrate this procedure might look like this:

Again, if you prefer to show three dots in each circle, as opposed to just writing the numeral 3, in each circle, that is perfectly fine. Either way, it should be clear from the drawing what procedure was used.
After disbursing all the cookies, you would count up how many baggies you were able to make, and that would give you the answer. Note the answer is 6, in this case. The model shown represents the multiplication [latex]6 \cdot 3[/latex], since there are 6 baggies of 3 cookies each.
The Model of division Word Problem B represents is called:
Repeated Subtraction or Measurement Model of Division
In this model, the divisor is the number of elements that will go into each subset/group. Each time the divisor (3) is subtracted from the dividend (18), a subset is formed. After all elements have been disbursed, the quotient (answer) is found by counting how many subsets were formed. This model is used when you are given how many elements are in each subset, and you are trying to find out how many subsets can be made (that is the question being asked). You do the division (by using repeated subtraction) to figure out how many subsets can be made. After doing the division, the number of subsets you made is the answer to the problem.
One way to distinguish that a problem suggests this model is to consider whether the information in the problem provides you with how many elements go into a subset. If so, as in Word Problem B, then it is the repeated subtraction model.
Word Problems requiring division generally fall into the category of Repeated Subtraction or Partitioning into Subsets. After reading a word problem, you should be able to analyze and interpret it as a problem that requires Partitioning into Subsets or Repeated Subtraction to solve the problem, and then be able to draw a picture using that model. Also, for any division problem given, you should be able to write two distinct word problems, one for each model, draw a picture for each model, and explain and show all the steps necessary to solve the problem.
Example 1
Solution:
- Partition - At the end of the day a bakery has 48 donuts leftover and 3 employees in the building. How many donuts does each employee get to take home if everyone gets an equal share?
We know how many subsets (aka piles) to make. We need to figure out how many go into each subset (pile). - Repeated Subtraction - The animal shelter uses 3 gallons of dog food a day. If they have 48 gallons of dog food, how many days can they feed their dogs?
We know how much we need in each subset (aka one day). We need to figure out how many subsets (days) that will make.
Connecting the Dots
Notice that the last picture from exercise 6 can represent both models of division for [latex]48\div 3[/latex] depending on if you look at the rows or the columns of the rectangle.
3 groups of size 16: 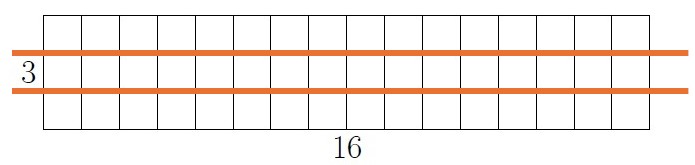
16 groups of size 3: 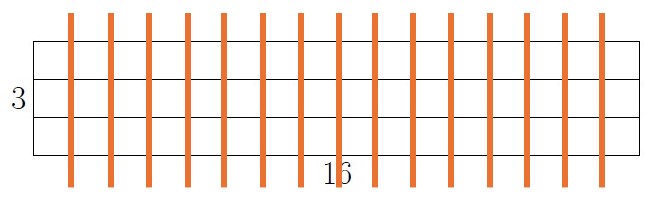
Which property of multiplication does this remind you of? It looks a lot like the commutative property. That's where our two models of division come from!
Exercises 7-12 are designed to help you distinguish between partitioning into subsets and repeated subtraction as well as work on your fluency with these techniques.
Exercise 7
Terry wanted to divide 100 marbles amongst his three best friends and himself. How many marbles would each of them get?
a. What division problem do you need to do to find the answer?
b. What model of division does this word problem represent?
c. Explain how to use the correct model to draw a picture to find the answer.
d. Draw a picture using the correct model to help find the answer.
e. Write the multiplication problem shown by the picture:
f. Explain how you use the picture to find the answer to the problem. Be specific.
g. What is the answer to this problem?
Solution
a. [latex]100\div 4[/latex]
b. Partitioning into subsets
c. Draw 4 circles and distribute marbles evenly into them until you have less than 4 marbles left.
d. 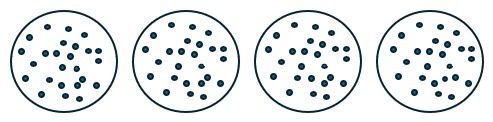
e. [latex]4\times 25[/latex]
f. The answer is the number of marbles (dots) inside each circle.
g. 25
Exercise 8
Jordan made 80 ounces of Jello, and wanted to put them in 8 ounce containers. How many containers can she fill?
a. What division problem do you need to do to find the answer?
b. What model of division does this word problem represent?
c. Explain how to use the correct model to draw a picture to find the answer.
d. Draw a picture using the correct model to help find the answer.
e. Write the multiplication problem shown by the picture:
f. Explain how you use the picture to find the answer to the problem. Be specific.
g. What is the answer to this problem?
Solution
a. [latex]80\div 8[/latex]
b. Repeated Subtraction
c. Start with 80 and repeatedly subtract 8 until you have less than 8 remaining.
d. 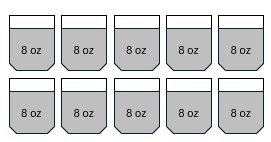
e. [latex]10\times 8[/latex]
f. The answer is the number of containers (groups) you were able to fill.
g. 10
Exercise 9
Angie had 144 pages of blank paper. She was making copies of a 16 page short story she wrote to send to magazines. How many complete copies could she make?
a. What division problem do you need to do to find the answer?
b. What model of division does this word problem represent?
c. Explain how to use the correct model to draw a picture to find the answer.
d. Draw a picture using the correct model to help find the answer.
e. Write the multiplication problem shown by the picture:
f. Explain how you use the picture to find the answer to the problem. Be specific.
g. What is the answer to this problem?
Solution
a. [latex]144\div 16[/latex]
b. Repeated subtraction
c. Start with 144 pages and keep subtracting one story (16 pages) until you have less than 16 pages remaining.
d. 
e. [latex]9\times 16[/latex]
f. The answer is the number stories you were able to print (the number of sixteens you were able to subtract).
g. 9
Exercise 10
A group of four friends pooled their money together for some lottery tickets and won $500. How much does each person receive from the winnings?
a. What division problem do you need to do to find the answer?
b. What model of division does this word problem represent?
c. Explain how to use the correct model to draw a picture to find the answer.
d. Draw a picture using the correct model to help find the answer.
e. Write the multiplication problem shown by the picture:
f. Explain how you use the picture to find the answer to the problem. Be specific.
g. What is the answer to this problem?
Solution
a. [latex]500\div 4[/latex]
b. Partitioning into subsets
c. Draw 4 circles and distribute the money evenly into them until you have less than $4 remaining.
d. 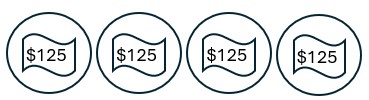
e. [latex]4\times 125[/latex]
f. The answer is the amount of money inside each circle.
g. 125
Exercise 11 (Extension Question)
Sheila wanted to make as many cakes from a recipe requiring [latex]1\frac{1}{3}[/latex] cups of flour for each cake. She had 8 cups of flour. How many cakes could she make?
- What division problem do you need to do to find the answer?
- What model of division does this word problem represent?
- Explain how to use the correct model to draw a picture to find the answer.
- Draw a picture using the correct model to help find the answer.
- Write the multiplication problem shown by the picture:
- Explain how you use the picture to find the answer to the problem. Be specific.
- What is the answer to this problem?
Solution
- [latex]8\div 1\frac{1}{3}[/latex]
- Repeated subtraction
- Draw 1 and 1/3 cups over and over until you have used all 8 cups or have less than 1 and 1/3 left.
- Number-line picture:

Cups picture:
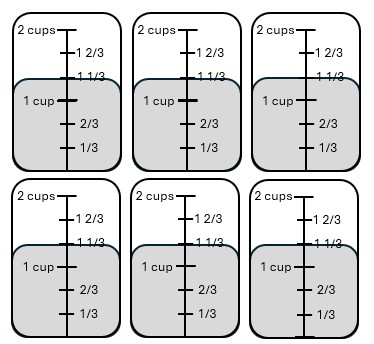
- [latex]6\times 1\frac{1}{3}[/latex]
- The answer is the number of 1 and 1/3 we were able to make.
- 6
Exercise 12
Tom won 65 baseballs and decided to divide them up evenly amongst the 13 boys on his baseball team. How many baseballs will each kid get?
- What division problem do you need to do to find the answer?
- What model of division does this word problem represent?
- Explain how to use the correct model to draw a picture to find the answer.
- Draw a picture using the correct model to help find the answer.
- Write the multiplication problem shown by the picture:
- Explain how you use the picture to find the answer to the problem. Be specific.
- What is the answer to this problem?
Solution
- [latex]65\div 13[/latex]
- Partitioning into subsets
- Draw 13 circles and distribute baseballs evenly into them until you have less than 13 baseballs left.
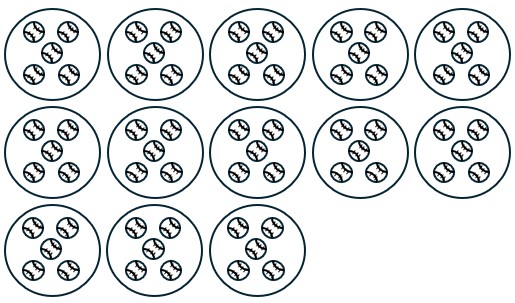
- [latex]13\times 5[/latex]
- The answer is the number of baseballs (dots) inside each circle.
- 5
If you are not presented with a word problem, but are simply given a division problem, you can use either model to think about and solve the problem. Many times, it is easier to use one model over another, especially if you need to draw a picture to show how you solved the problem.
Consider the following division problem: [latex]26 \div 2[/latex]. Let’s say the 26 represented pennies. Would it be easier to partition 26 pennies into 2 piles and count how many are in each pile; or would it be easier to make several equal subsets containing 2 pennies each from the 26 pennies, and then to count how many subsets there are? The picture you draw to represent each model is quite different. Look at the difference:
Partition:
Repeated Subtraction:

Exercise 13
For parts a - h of this exercise, consider the division problem: [latex]48 \div 12[/latex].
- Which model do you think would be easier to use if you needed to draw a picture?
- Explain why the model you chose in part a would be easier to use.
- Make up a word problem requiring the division [latex]48 \div 12[/latex], such that the partitioning into subsets model is used. Make sure your problem asks a question!
- Draw a picture to solve your problem using the partitioning into subsets model.
- Give the multiplication equation for the picture shown in part d.
- Make up a word problem requiring the division [latex]48 \div 12[/latex], such that the repeated subtraction model is used. Make sure your problem asks a question!
- Draw a picture to solve your problem using the repeated subtraction model.
- Give the multiplication equation for the picture shown in part g.
Answers will vary.
Exercises 14
For parts a - h of this exercise, consider the division problem: [latex]200 \div 4[/latex].
- Which model do you think would be easier to use if you needed to draw a picture?
- Explain why the model you chose in part a would be easier to solve this division problem. Contrast it with the other model.
- Make up a word problem requiring the division [latex]200 \div 4[/latex], such that the partitioning into subsets model is used. Make sure your problem asks a question!
- Draw a picture to solve your problem using the partitioning into subsets model.
- Give the multiplication equation for the picture using partitioning into subsets.
- Make up a word problem requiring the division [latex]200 \div 4[/latex], such that the repeated subtraction model is used. Make sure your problem asks a question!
- Explain what you would have to do if you had to draw a picture to solve your problem using the repeated subtraction model. Do not actually draw the picture — just explain.
- Give the multiplication equation for the picture using repeated subtraction.
Answers will vary.
Exercise 15
For parts a - h of this exercise, consider the division problem: [latex]150 \div 50[/latex].
- Which model do you think would be easier to use if you needed to draw a picture?
- Explain why the model you chose in part a would be easier to solve this division problem. Contrast it with the other model.
- Make up a word problem requiring the division [latex]150 \div 50[/latex], such that the partitioning into subsets model is used. Make sure your problem asks a question!
- Explain what you would have to do if you had to draw a picture to solve your problem using the partitioning into subsets model. Do not actually draw the picture — just explain!
- Give the multiplication equation for the picture using partitioning into subsets.
- Make up a word problem requiring the division [latex]150 \div 50[/latex], such that the repeated subtraction model is used. Make sure your problem asks a question!
- Draw a picture to solve your problem using the repeated subtraction model:
- Give the multiplication equation for the picture using repeated subtraction.
Answers will vary.
Exercise 16
For each division problem, a picture is shown. Based on the picture, state which model of division was used.
- [latex]84\div 21[/latex]

- [latex]85 \div 5[/latex]

- [latex]30 \div 5[/latex]

- [latex]30 \div 6[/latex]

Solution
(a) repeated subtraction
(b) partitioning into subsets
(c) partitioning into subsets
(d) repeated subtraction.
Exercise 17
For each picture, a particular model of division was used to solve a division problem. Based on the model and picture, decide what the original division problem was.
- Repeated subtraction

- Partitioning into subsets

Exercise 18
For each picture, a particular model of division was used to solve a division problem. Based on that model and picture, state the original division problem with its answer.
a. Partitioning into subsets

b. Repeated subtraction

Exercise 19
Using the definition of multiplication from Module 4, if you drew a picture for the multiplication problem, [latex]a \cdot b[/latex], which letter represents how subsets are made, and which letter represents how many are in each subset?
Solution
There are [latex]a[/latex] subsets and each one has [latex]b[/latex]-many things in it.
While these models are a great way to visualize division, they are not technical definitions. The actual definition relies on the fact that division is the operation that undoes multiplication. Students can rely on this fact to learn basic division facts. For instance, since 6 [latex]\cdot[/latex] 7 = 42, then [latex]42 \div 6 = 7[/latex] and [latex]42 \div 7 = 6[/latex].
Missing Factor Model and Definition of Division
When solving the division problem [latex]20/div 5[/latex], many people think "5 times what number equals 20?" This is called the missing factor model of division because you are looking for the missing factor. This method of thinking is formalized by the definition of division.
Definition - [latex]\color{white}a\div b[/latex]
Instead of writing c, it is sometimes easier to write a blank or box in the equations to see if a unique solution exists. If you can put a unique solution in the blank to the multiplication problem, then you can go back and fill in the solution to the division problem.
Teaching Tip: Giving students equations with boxes like [latex]72=8\cdot\square[/latex] helps prepare students for algebra later where the box will be replaced with [latex]x[/latex].
Example 2
Use the definition of division to find the answer to [latex]21 \div 3[/latex].
Thought process
First, note that [latex]21 \div 3=\underline{\qquad}[/latex] means [latex]21 = 3 \cdot\underline{\qquad}[/latex]. Second, try to fill in the blank in the multiplication problem with a unique number to make the equation, [latex]21 = 3 \cdot\underline{\qquad}[/latex], true: [latex]21 = 3 \cdot \underline{7}[/latex]. If the number filled in is the only possible solution (unique), then that is the answer to the division problem. Therefore, [latex]21 \div 3[/latex] = [latex]\underline{7}[/latex]. You do not need to write this paragraph for your solution. Below is how to write the solution.
Solution
Since [latex]21 = 3 \cdot \underline{7}[/latex], then [latex]21 \div 3 = \underline{7}[/latex].
Exercise 20
Use the definition of division to find the following quotients:
a. [latex]32 \div 8[/latex]
Solution
Since [latex]32 = 8 \cdot \underline{4}[/latex], then [latex]32 \div 8 = \underline{4}[/latex].
b. [latex]56 \div 8[/latex]
Solution
Since [latex]56 = 8 \cdot \underline{7}[/latex], then [latex]56 \div 8 = \underline{7}[/latex].
c. [latex]32 \div 2[/latex]
Solution
Since [latex]32 = 2 \cdot \underline{16}[/latex], then [latex]32 \div 2 = \underline{16}[/latex].
d. [latex]0 \div 13[/latex]
Solution
Since [latex]0 = 13 \cdot \underline{0}[/latex], then [latex]0 \div 13 = \underline{0}[/latex].
e. [latex]12 \div 1[/latex]
Solution
Since [latex]12 = 1 \cdot \underline{12}[/latex], then [latex]12 \div 1 = \underline{12}[/latex].
f. [latex]X \div 1[/latex] (Assume X is any number.)
Solution
Since [latex]X = 1 \cdot \underline{X}[/latex] for any X, then [latex]X \div 1 = \underline{X}[/latex].
g. [latex]0 \div Y[/latex] (Assume Y is any nonzero number.)
Solution
Since [latex]0 = Y \cdot \underline{0}[/latex] for any nonzero Y, then [latex]0 \div Y = \underline{0}[/latex].
Exercise 20f illustrates that any number divided by 1 is itself.
In other words,
[latex]\bf a \div 1 = a[/latex] for all values of a.
Exercise 20g illustrates that zero divided by any nonzero whole number is 0.
In other words,
[latex]\bf 0 \div a = 0[/latex], for all nonzero values of a.
Why did we specify nonzero values of a? You have always heard “You cannot divide by zero,” but why is that? Let’s explore division by zero using our models and our definition.
Example 3
a. Use the definition of division to find the quotient: [latex]\bf 8 \div 0[/latex].
Thought Process
Note that [latex]8 \div 0=\underline{\qquad}[/latex] means [latex]8 = 0 \cdot\underline{\qquad}[/latex]. Now, try to fill in the blank in the multiplication problem with a unique number to make the equation, [latex]8 = 0 \cdot\underline{\qquad}[/latex], true. There is no number that can be put in the blank to make that equation true since any number times 0 is 0, and will never equal 8. This is how you could write the solution:
Solution to a.
There is no number that will make the equation, [latex]8 = 0 \cdot\underline{\qquad}[/latex] true, since any number put in the blank will make the right hand side of the equation zero, which can never equal the left-hand side of the equation, which is 8. Therefore, [latex]8 \div 0[/latex] is not defined.
b. Use the partitioning by subsets model to find the quotient: [latex]\bf 8 \div 0[/latex].
Thought Process
By the partitioning into subsets model, [latex]\bf 8 \div 0[/latex] would mean we have 8 items to put into zero subsets. We have nowhere to put the 8 items, but they cannot vanish into nothingness. They have to go somewhere! Thus, the division statement is undefined.
Solution to b.
You cannot put 8 items into 0 subsets. Thus, [latex]8 \div 0[/latex] is not defined.
c. Use the repeated subtraction model to find the quotient: [latex]\bf 8 \div 0[/latex].
Thought Process
We must repeatedly subtract 0 until we reach a positive number smaller than zero. So, we have
[latex]8-0=8[/latex]
[latex]8-0=8[/latex]
[latex]8-0=8[/latex]
[latex]8-0=8[/latex]
[latex]8-0=8[/latex]
[latex]\vdots[/latex]
This process will never end. We are never going to get a positive number smaller than zero.
Solution to c.
If you use repeated subtraction and keep subtracting zero, you will never finish. Ergo, [latex]8\div 0[/latex] is undefined.
Exercise 21
Use the given method to show that the following quotients are undefined:
a. [latex]6 \div 0[/latex], repeated subtraction
Solution
If you try to subtract 0 from 6, you will never reach an end. You can subtract 0 forever. [latex]6-0=6-0=6-0=6-0=\cdot\cdot\cdot[/latex] So, [latex]6\div 0[/latex] has no solution.
b. [latex]18 \div 0[/latex], partitioning by subsets
Solution
If you have 18 items you cannot put them into zero groups. They cannot disappear into thin air. They have to go somewhere! So [latex]18 \div 0[/latex] has no solution.
c. [latex]M \div 0[/latex] (Assume [latex]M \neq 0[/latex]), definition of division
Solution
If [latex]M \div 0=A[/latex] for some number [latex]A[/latex], that means that [latex]0\times A=M[/latex]. But [latex]0\times A=0[/latex] and [latex]M \neq 0[/latex], so this is impossible. Thus, if [latex]M \neq 0[/latex], [latex]M \div 0[/latex] has no solution.
Classroom Connection: You ask your students to justify why [latex]8\div 0[/latex] has no solution. One group gives the answer below. What is their error? How can you help them?
We think [latex]8\div 0[/latex] has no solution because you cannot divide by 0. If you rewrite it to get [latex]8=0\cdot\underline{\qquad}[/latex] there is nothing that can go in the blank. Since there is nothing, the answer is zero.
Solution
The students are saying [latex]8\div 0=0[/latex], which is not true! They might be
confusing "nothing" with meaning zero. But in this context, "nothing" means no number at all, not even zero.
In exercise 20, you showed that dividing a nonzero number by 0 was undefined. Now, let's explore what happens if we divide zero by zero.
Example 4
Use the definition of division to find the quotient: [latex]\bf 0 \div 0[/latex].
Thought Process
First, note that [latex]0 \div 0=\underline{\qquad}[/latex] means [latex]0 = 0\cdot\underline{\qquad}[/latex]. Second, try to fill in the blank in the multiplication problem with a unique number to make the equation, [latex]0 = 0\cdot\underline{\qquad}[/latex], true. There is no unique number that can be put in the blank to make that equation true since any number put in the blank will make the equation true, and therefore there is no unique number that will work. This is how you could write the solution:
Solution
There are lots of numbers that can be put in the blank to make the equation [latex]0 = 0\cdot\underline{\qquad}[/latex] true, so there is not a unique solution. Therefore, [latex]0 \div 0[/latex] is called indeterminate.
Recall that our definition says that when considering [latex]a=b\cdot c[/latex], if there is no number, c, that exists, or if there is more than one unique number that can be put in for c, then [latex]a \div b[/latex] is said to be undefined. The "more than one" condition was added specifically for [latex]0\div 0[/latex].
To prove that division by zero is undefined, two cases must be shown. Below is a complete proof to show that division by zero is undefined.
Problem: Prove that division by zero is undefined
Solution: The goal is to show that [latex]a \div 0[/latex] is undefined for all values of a. There are two cases to consider, either [latex]a \neq 0[/latex] or [latex]a = 0[/latex].
Case 1: Let [latex]a \neq 0[/latex]. There is no unique number that could be put in the blank to make the equation, [latex]a = 0 \cdot\underline{\qquad}[/latex], true because the left-hand side of the equation is not zero (since [latex]a \neq 0[/latex]), and any number put in the blank will make the right hand side of the equation zero. Therefore, when [latex]a \neq 0[/latex], [latex]a \div 0[/latex] is not defined.
Case 2: Let [latex]a = 0[/latex]. There is no unique number that can be put in the blank to make the equation [latex]0 = 0 \cdot\underline{\qquad}[/latex] true, since any number will make it true. Therefore, [latex]0 \div 0[/latex] is indeterminate.
It takes practice writing this proof. You'll need to practice writing it several times to master the problem. As you rewrite it over and over, focus on the flow of the logic until you really get the idea. Being able to express oneself precisely in mathematical language shows a deep level of understanding necessary to be a high-quality teacher.
Exercise 22
Prove that division by zero is undefined.
So far, when using the definition of division, we have limited ourselves to problems where the answers were whole numbers or the problem divided by zero and was undefined. If you were asked to use the definition to find only whole number solutions, then some non-zero divisions, such as [latex]15\div 2[/latex] would be undefined under the whole numbers. There may, however, be rational or irrational solutions depending on the problem. For example, [latex]15=2\cdot 7.5[/latex]. Even though there is a possible solution in the rational numbers, we say [latex]15\div 2[/latex] is undefined under the whole numbers, because the solution is not a whole number.
Example 5
Use the definition of division to find if [latex]\bf 21 \div 5[/latex] is defined under whole numbers. Show the solution if it is defined, or explain why not if it is not defined.
Thought Process
First, note that [latex]21 \div 5=\underline{\qquad}[/latex] means [latex]21 = 5 \cdot\underline{\qquad}[/latex]. Second, try to fill in the blank in the multiplication problem with a unique whole number to make the equation, [latex]21 = 5 \cdot\underline{\qquad}[/latex], true. There is no whole number that can be put in the blank to make that equation true. Therefore, [latex]21 \div 5[/latex] is not defined under whole numbers. Here is how you would show the answer.
Solution
Since there is no whole number solution to make the equation, [latex]21 = 5 \cdot\underline{\qquad}[/latex] true, [latex]21 \div 5[/latex] is not defined under whole numbers.
Exercise 23
Use the definition of division to find which of the following quotients are defined under whole numbers. If it is defined, show the solution and justify your answer. If it is not defined, explain why using the definition of division.
a. [latex]45 \div 5[/latex]
Solution
Since [latex]45 = 5 \cdot \underline{9}[/latex], then [latex]45 \div 5 = \underline{9}[/latex].
b. [latex]42 \div 9[/latex]
Solution
Since there is no whole number solution to make the equation [latex]42 = 9 \cdot \underline{\qquad}[/latex] true, [latex]42 \div 9[/latex] is not defined under the whole numbers.
c. [latex]48 \div 6[/latex]
Solution
Since [latex]48 = 6 \cdot \underline{8}[/latex], then [latex]48 \div 6 = \underline{8}[/latex].
d. [latex]35 \div 4[/latex]
Solution
Since there is no whole number solution to make the equation [latex]35 = 4 \cdot \underline{\qquad}[/latex] true, [latex]35 \div 4[/latex] is not defined under the whole numbers.
e. [latex]48 \div 1[/latex]
Solution
Since [latex]48 = 1 \cdot \underline{48}[/latex], then [latex]48 \div 1 = \underline{48}[/latex].
f. [latex]55 \div 7[/latex]
Solution
Since there is no whole number solution to make the equation [latex]55 = 7 \cdot \underline{\qquad}[/latex] true, [latex]55 \div 7[/latex] is not defined under the whole numbers.
g. [latex]0 \div 8[/latex]
Solution
Since [latex]0 = 8 \cdot \underline{0}[/latex], then [latex]0 \div 8 = \underline{0}[/latex].