12 Trading and Place Value
Louisiana Student Standards
Standard Number |
Description of Standard |
| K.CC.A.3 | Write numbers from 0 to 20. Represent a number of objects with a written numeral 0–20 (with 0 representing a count of no objects). |
| K.NBT.A.1.a | Understand that the numbers 11–19 are composed of ten ones and one, two, three, four, five, six, seven, eight, or nine ones. |
| K.NBT.A.1.b | Compose and decompose numbers 11 to 19 using place value (e.g., by using objects or drawings). |
| K.NBT.A.1.c | Record each composition or decomposition using a drawing or equation (e.g., 18 is one ten and eight ones, 18 = 1 ten + 8 ones, 18 = 10 + 8). |
| 1.NBT.A.1 | Count to 120, starting at any number less than 120. In this range, read and write numerals and represent a number of objects with a written numeral. |
| 1.NBT.B.2 | Understand that the two digits of a two-digit number represent amounts of tens and ones. |
| 2.NBT.A.1 | Understand that the three digits of a three-digit number represent amounts of hundreds, tens, and ones; e.g., 706 equals 7 hundreds, 0 tens, and 6 ones. |
| 2.NBT.A.3 | Read and write numbers to 1000 using base-ten numerals, number names, and expanded form. |
You will need: Arcade Prize Tokens (Material Card 3) and Base Blocks (Material Cards 4-16).
Exploration Activity
Use your cut out Arcade Prize Tokens to follow along with the scenario below. Do not use a calculator!
The High Five Arcade has a special system for earning prizes. As you play games, you can earn “prize tokens” in the values of one, five, twenty-five, one hundred twenty-five, and six hundred twenty-five prize points. Your goal is to earn 1000 points to win the big prize!
After playing games for an hour, you have earned the following:
- 19 one point tokens
- 19 five point tokens
- 6 twenty-five point tokens
Carrying around so many prize tokens is getting annoying, so you go to the counter and exchange them for the fewest number of prize tokens possible. How many of each token type do you have after you exchange them? (You may have a shortcut way to do this, but use your cut-out Arcade Prize Tokens and physically exchange them. It will help you later!)
In the next game, you win the grand prize and earn one of each prize token type. You go back to the counter to again exchange your prize tokens for the fewest number possible. Now, how many of each token type do you have?
You can now claim the 1000 point big prize! After you claim your prize, how many of each token type do you have left? (You may use a calculator for this part.)
Notice how whenever you had five of one type of prize token, you were able to exchange it for one of the next size up. These tokens model a base five numeration system.
Base Ten Numerals
The Hindu-Arabic system is a base ten system. Each place value is made up of ten of the previous place value. Consider the number 2,385. You probably read that in your head as “two thousand, three hundred, eighty-five.” You are automatically recognizing the place value of each piece. The digit 2 is in the thousands place, the digit 3 is in the hundreds place, the digit 8 is in the tens place, and the digit 5 is in the ones place. This means there are 2 things of size one thousand, 3 things of size one hundred, 8 things of size ten, and 5 things of size one. Here are the first five place values in the base ten system.
Ten Thousands |
Thousands |
Hundreds |
Tens |
Ones |
| 10000 | 1000 | 100 | 10 | 1 |
| 10[latex]\times[/latex]1000 | 10[latex]\times[/latex]100 | 10[latex]\times[/latex]10 | 10[latex]\times[/latex]1 | 1 |
| 10[latex]^{4}[/latex] | 10[latex]^{3}[/latex] | 10[latex]^{2}[/latex] | 10[latex]^{1}[/latex] | 10[latex]^{0}[/latex] |
Notice how, as you move from the right to the left, each new place value is ten times the previous one. This is why our place values are all powers of 10.
In elementary classrooms, whole numbers are often represented with base ten blocks.
Thousands |
Hundreds |
Tens |
Ones |
 |
 |
||
| Cubes | Flats | Longs | Units |
Notice how each piece, when you join ten of them in a row, creates the next piece: 10 joined units make a long, 10 joined longs make a flat, and 10 joined flats make a cube.
Example
Determine the least number of base ten blocks that can be used to represent the given block arrangement. Then give the base ten numeral for the number represented.
23 units, 13 longs, and 4 flats
Solution: Laying out our blocks we have the following.
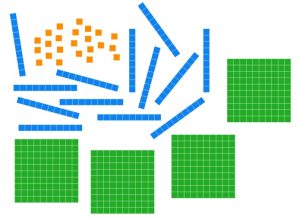
Each group of ten unit pieces can be traded for a long.
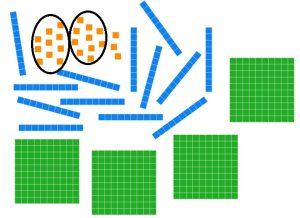
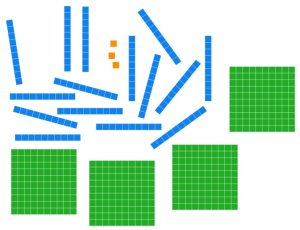
Ten long pieces can be traded for a flat.
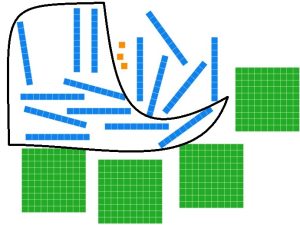
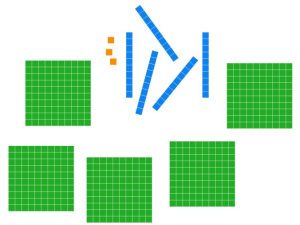
No more trades can be made, so we are done.
5 flats, 5 longs, and 3 units.
Base ten numeral: 553
Pull out your cut out Units (Material Card 4) and Base Ten Blocks (Material Card 13) and answer the following questions.
Exercise 1
For each of the following state the least number of base ten blocks of each type needed to represent the number, then give the base ten numeral. Do not use a calculator!
a. 17 units, 9 longs, 5 flats
b. 24 units, 11 longs, 9 flats
c. 10 units, 9 longs, 9 flats, 8 cubes
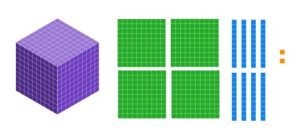
Exercise 2
a. What base ten numeral is shown below?

Solution
The base ten numeral is 357
b. Draw the base ten block representation of 1482.
Solution
You may have found a shortcut when solving exercise 1. For example, consider part (b). If you add the values of the blocks, you get [latex](24\times 1)+(11\times 10)+(9\times 100)=1034.[/latex] This means you will have 1 cube, 0 flats, 3 longs, and 4 units. The reason you can do this trick is that you already know base ten. Your future students do not have this advantage! In order to put you in their shoes, we need to consider other number bases. As you are working through this section, be thinking of what questions your future students might have and how you can answer them.
Base Seven Numerals
Examine your cut out Units (Material Card 4) and Base Seven Blocks (Material Card 8) and answer the following questions.
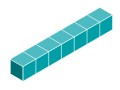
Exercise 3
a. How many units does it take to make one base seven long?
Solution
It takes seven units to make a long.
b. How many base seven longs does it take to make one base seven flat?
Solution
It takes seven longs to make a flat.

c. How many base seven flats does it take to make one base seven cube?
Solution
It takes seven flats to make a cube.

d. What are the first four place values in base seven?
Solution
ones
sevens
forty-nines
three-hundred-forty-threes
Example
Determine the least number of base seven blocks that can be used to represent the given base seven block arrangement. Then give the base seven numeral for the number represented.
9 units, 12 longs
Solution: Our starting lay out of blocks has nine units and twelve longs.

Seven units have the same value as one long, so we can trade seven of the units for a long.
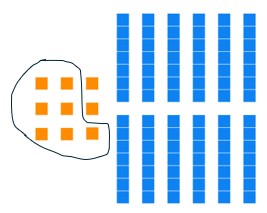
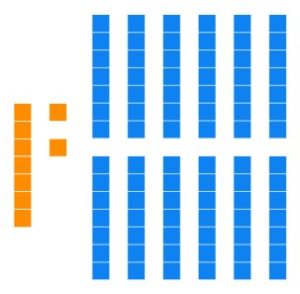
Seven longs have the same value as one flat, so we can trade seven longs for one flat.
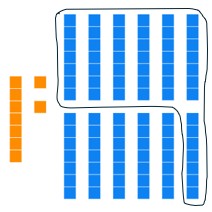

All of our block types have less than seven each, so we are done trading! Our answer is
1 flat, 6 longs, 2 units
Base seven numeral: 162[latex]_{\text{seven}}[/latex]
When 162[latex]_{\text{seven}}[/latex] is read aloud we say “one six two base seven.” Do not say “one hundred sixty-two base seven.” That doesn’t make sense. The 1 is in the 49’s place, not in the hundreds place, so it is not a hundred. The 6 is in the 7’s place, not the tens place, so it is not sixty. Form the habit now of reading all numerals that are not in base ten this way. It will save you from a lot of confusion later!
Exercise 4
For each of the following state the least number of base seven blocks of each type needed to represent the base seven blocks given, then give the base seven number. Do not use a calculator!
a. 8 units, 8 longs, 3 flats
b. 21 units, 6 longs, 6 flats
Exercise 5
a. What base seven number is shown below?
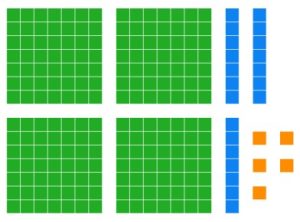
Solution
[latex]435_{\text{seven}}[/latex]
b. Draw the base seven block representation of 5064[latex]_{\text{seven}}[/latex]
Solution

Now that you are getting comfortable with the blocks, let’s look at how they help us count. Start with one unit. That is the number one. Now put down another unit. That is the number two. This continues until we have reached our trading point (which in base seven is seven). Then all seven units can be traded for a long. Here are the first ten numbers represented in base seven.
| Number | Representation in Base Seven Blocks | Base seven numeral | Pronunciation |
|---|---|---|---|
| One |  |
[latex]1_{\text{seven}}[/latex] | one base seven |
| Two |  |
[latex]2_{\text{seven}}[/latex] | two base seven |
| Three |  |
[latex]3_{\text{seven}}[/latex] | three base seven |
| Four |  |
[latex]4_{\text{seven}}[/latex] | four base seven |
| Five |  |
[latex]5_{\text{seven}}[/latex] | five base seven |
| Six |  |
[latex]6_{\text{seven}}[/latex] | six base seven |
| Seven |  |
[latex]10_{\text{seven}}[/latex] | one zero base seven |
| Eight |  |
[latex]11_{\text{seven}}[/latex] | one one base seven |
| Nine | 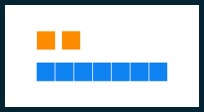 |
[latex]12_{\text{seven}}[/latex] | one two base seven |
| Ten | 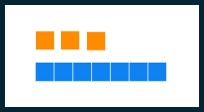 |
[latex]13_{\text{seven}}[/latex] | one three base seven |
Caution: It is easy to look at 10[latex]_{\text{seven}}[/latex] and think “ten.” Remember that ten represents the concept of ten items and can be written in lots of different ways. In base seven, one long and zero units is not the same as a base ten long and zero units. Think of it this way, the Spanish word for cat (gato) sounds almost identical to the French word for cake (gateaux), but they are very different things! You need to pay attention to which language you are in!
Example
Use your base seven blocks to help you find the following base seven numerals.
a. What is the base seven numeral preceding (before) 30[latex]_{\text{seven}}[/latex]?
Solution: Start with 3 base seven longs.

To get the number just before this number, we need to remove one unit. This means we need to break down one of the longs into seven units. Then we can remove one of them.
This leaves behind 2 longs and 6 units.
Answer: [latex]26_{\text{seven}}[/latex]
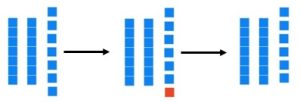
b. What is the base seven numeral succeeding (after) 56[latex]_{\text{seven}}[/latex]?
Solution: We are starting with 5 base seven longs and 6 units.
Since we want the number after our given number, we need to add one unit. This gives us seven units total, which can be grouped into one long.
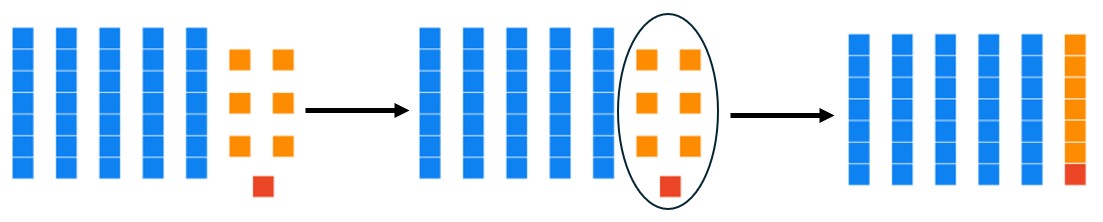
Thus we have 6 longs and zero units.
Answer: [latex]60_{\text{seven}}[/latex]
Exercise 6
Use your base seven blocks to help you find the following base seven numerals.
a. What is the base seven numeral preceding (before) 23[latex]_{\text{seven}}[/latex]?
b. What is the base seven numeral succeeding (after) 23[latex]_{\text{seven}}[/latex]?
c. What is the base seven numeral preceding 46[latex]_{\text{seven}}[/latex]?
d. What is the base seven numeral succeeding 46[latex]_{\text{seven}}[/latex]?
e. What is the base seven numeral preceding 100[latex]_{\text{seven}}[/latex]?
f. What is the base seven numeral succeeding 100[latex]_{\text{seven}}[/latex]?
Concept Check:
a. What is wrong with the following base seven numeral?
[latex]519_{\text{seven}}[/latex]
Solution
If you have nine units in base seven, the units must be traded to make a base seven long. This means you cannot have the digit nine in any place-value in base seven.
b. What are the only digits that will ever appear in any base seven numeral?
Solution
The only digits will be 0, 1, 2, 3, 4, 5, and 6 since the moment you have 7 of any place value, you must trade them for one of the next place value.
Now that we have a visual for how base seven works, we can extend to even higher place values. So far we have place values
| Cubes | Flats | Longs | Units |
| 343 | 49 | 7 | 1 |
| 7[latex]^3[/latex] | 7[latex]^2[/latex] | 7[latex]^1[/latex] | 7[latex]^0[/latex] |
Exercise 7
a. Even though we don’t have blocks to represent them, what are the next two place values after (larger than) 343?
b. What is the base seven numeral succeeding 66666[latex]_{\text{seven}}[/latex]?
c. What is the value of your answer in part (b)?
One way to visualize the value of our numerals is to look at them in expanded form. For example, the base seven numeral 52463[latex]_{\text{seven}}[/latex] can be separated into its place values and written as
[latex](5\times 7^4) + (2\times 7^3) + (4\times 7^2) + (6\times 7) + (3\times 1)[/latex] or
[latex](5\times 2401) + (2\times 343) + (4\times 49) + (6\times 7) + (3\times 1)[/latex].
Notice how this form really shows what each separate digit of the numeral represents.
Exercise 8
Write each base seven numeral in expanded form.
a. [latex]3055_{\text{seven}}[/latex]
b. [latex]10632_{\text{seven}}[/latex]
Base Five Numerals
Remember our introductory activity with the Arcade Prize Tokens? It took five of each coin to make the next size. That’s a base five system. If we use the more traditional blocks to visualize base five, we have the following pieces.
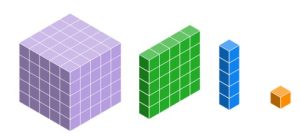
Exercise 9
Examine your Base Five Blocks (Material Card 8) and use them to help answer the following questions.
a. What is the value of each block type (unit, long, flat, cube) in base five?
Solution
In base five, a unit has a value of one, a long has a value of five, a flat has a value of twenty-five, and a cube has a value of one-hundred-twenty five.
b. What are the first four place values in base five?
Solution
125’s, 25’s, 5’s, 1’s
Exercise 10
a. What base five number is shown below?
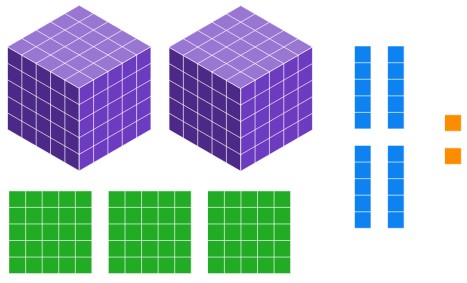
Solution
[latex]2342_{\text{five}}[/latex]
b. Draw the base five block representation of 1422[latex]_{\text{five}}[/latex]
Solution
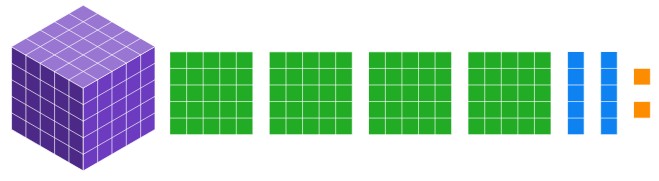
c. Write 1422[latex]_{\text{five}}[/latex] in expanded form.
Exercise 11
List the first twenty-five counting numbers using base five numerals. Use your blocks if you are stuck!
How did you do with exercise 11? Were you able to list all twenty-five numerals on the first try? If so, that’s great! You are starting to really understand place value. If not, that’s okay. This is how your future students will feel when you write ” …98, 99, 100, 101,…” That jump from 99 to 100 seems bizarre and out of the blue to them, too. Keep working, and eventually it will click.
Exercise 12
Use your base five blocks to help you find the following base five numerals.
a. What is the base five numeral preceding (before) 300[latex]_{\text{five}}[/latex]?
b. What is the base five numeral succeeding (after) 300[latex]_{\text{five}}[/latex]?
c. What is the base five numeral preceding 444[latex]_{\text{five}}[/latex]?
d. What is the base five numeral succeeding 444[latex]_{\text{five}}[/latex]?
Recall how we extended from our blocks to higher place values in base seven. This works in any number base. For base five our blocks represent:
| Cubes | Flats | Longs | Units |
| 125 | 25 | 5 | 1 |
| 5[latex]^3[/latex] | 5[latex]^2[/latex] | 5[latex]^1[/latex] | 5[latex]^0[/latex] |
Exercise 13
a. In base five, what would the next three place values be after (larger than) 125?
b. Write the base five numeral 324012[latex]_{\text{five}}[/latex] in expanded form.
Now that you have worked with three different number bases, it is time to compare them and look for commonalities.
Exercise 14
Think about how your numerals progressed in base five vs. base seven vs. base ten.
a. What is the largest digit before you trade/exchange in base five?
Solution
The largest digit in base five is a 4 because you must trade if you have five or more.
b. What is the largest digit before you trade/exchange in base seven?
Solution
The largest digit in base seven is 6 because you must trade if you have seven or more.
c. What is the largest digit before you trade/exchange in base ten?
Solution
The largest digit in base ten is 9 because you must trade if you have ten or more.
d. What do you think will be the largest digit before you trade/exchange in base 9?
Solution
The largest digit in base nine should be an 8 because you must trade if you have nine or more.
e. What do you think will be the largest digit before you trade/exchange in base 2?
Solution
The largest digit in base two should be a 1 because you must trade if you have two or more.
f. What do you think will be the largest digit before you trade/exchange in base 12?
Solution
The largest digit in base twelve should be an eleven because you must trade if you have twelve or more.
So, there are only five symbols that will ever appear in a base five numeral: 0, 1, 2, 3, 4. In base seven, we need seven symbols: 0, 1, 2, 3, 4, 5, 6. In base ten, we need ten symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. This pattern works for any number base!
You may have thought something was funny about your answers to exercise 14 parts (e) and (f). We should take a closer look at these two bases.
Base Two Numerals
In base two, our place values will be based on powers of two. So our blocks each represent the value
Units – 1
Longs – 2
Flats – 4
Cubes – 8
This means the number eight expressed as a base two numeral is [latex]1000_{\text{two}}[/latex]. Apparently, we will need a fifth place value very early on in counting. It will help if we make blocks for the next few place values. Look at the blocks below and make sure you see how each one is two times the one to its right.
Cube Cube |
Flat Cube |
Long Cube |
Cube |
Flat |
Long |
Unit |
 |
 |
 |
 |
 |
 |
 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| [latex]2^6[/latex] | [latex]2^5[/latex] | [latex]2^4[/latex] | [latex]2^3[/latex] | [latex]2^2[/latex] | [latex]2^1[/latex] | [latex]2^0[/latex] |
Exercises 15
a. How many symbols are needed in base two? What are they?
Solution
You need two symbols: 0 and 1.
b. List the first twenty five counting numbers using base two numerals. (Remember that in exercise 14 part (e) we said that 1 is the largest digit in base two!) Think about the blocks if you are stuck!
Base two seems strange because the numerals grow in length very quickly. It is still the exact same numbers you are used to; they are just in a different language from your native base ten.
Exercise 16
Use your base two blocks to help you find the following base two numerals.
a. What is the base two numeral preceding (before) 101[latex]_{\text{two}}[/latex]?
b. What is the base two numeral succeeding (after) 101[latex]_{\text{two}}[/latex]?
c. What is the base two numeral preceding 1111[latex]_{\text{two}}[/latex]?
d. What is the base two numeral succeeding 1111[latex]_{\text{two}}[/latex]?
e. What is the base two numeral preceding 10000[latex]_{\text{two}}[/latex]?
f. What is the base two numeral succeeding 10000[latex]_{\text{two}}[/latex]?
Exercise 17
a. Draw the base two block representation of 101011[latex]_{\text{two}}[/latex].
Solution
b. Write the base two numeral 101011[latex]_{\text{two}}[/latex] in expanded form.
For more practice with base two, see section 3-5 Supplementary Topics.
Base Twelve Numerals
| Cubes | Flats | Longs | Units |
| 1728 | 144 | 12 | 1 |
| 12[latex]^3[/latex] | 12[latex]^2[/latex] | 12[latex]^1[/latex] | 12[latex]^0[/latex] |
Exercise 18
For each picture below, give the base twelve numeral shown, then write that numeral in expanded form. (If necessary, trade so that you have the least number of blocks possible.)
a.

b.

c.

Solution
There are 8 longs and eleven units, but we haven’t learned how to write that yet.
What happened on part (c) of the last exercise? If you wrote [latex]811_{\text{twelve}}[/latex], it probably looked wrong (and it is) but what else can you do? There are eleven units left after exchanging. We need a way to say “eleven things are in this place value.” Consider the symbols we already have: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. The list is only ten symbols, but base twelve needs twelve symbols. Since base twelve is not a standard base, there are no standard symbols for “ten things are in this place value” and “eleven things are in this place value.” We will use [latex]\text{T}[/latex] and [latex]\text{E}[/latex], respectively. We will use these same symbols in bases eleven and thirteen as well. If you are in base thirteen and need “twelve things are in this place value” use [latex]\text{W}[/latex].
Definition – T, E, and W
- The digits in base eleven are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and T where T represents the quantity ten.
- The digits in base twelve are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, T, and E where T represents the quantity ten and E represents the quantity eleven.
- The digits in base thirteen are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, T, E, and W where T represents the quantity ten, E represents the quantity eleven, and W represents the quantity twelve.
Exercise 18 (Revisited)
For the picture below, give the base twelve numeral shown, then write that numeral in expanded form. (If necessary, trade so that you have the least number of blocks possible.)

Exercise 19
List the first twenty-five counting numbers using base twelve numerals. Think about the blocks if you are stuck!
Exercise 20
Find the following base twelve numerals. Use your blocks if you are stuck!
a. What is the base twelve numeral preceding (before) EEE[latex]_{\text{twelve}}[/latex]?
b. What is the base twelve numeral succeeding (after) EEE[latex]_{\text{twelve}}[/latex]?
c. What is the base twelve numeral preceding T0[latex]_{\text{twelve}}[/latex]?
d. What is the base twelve numeral succeeding T0[latex]_{\text{twelve}}[/latex]?
If you can handle bases two and twelve, then you are a place value whiz! As long as you are comfortable with at least one base that is not base ten, you should have the depth of knowledge required to answer whatever base ten questions your students come up with!
Summary
Consider the table below and answer the questions in Exercise 21.
| Number | Base Two | Base Four | Base Five | Base Seven | Base Ten | Base Twelve |
|---|---|---|---|---|---|---|
| One | [latex]1_{\text{two}}[/latex] | [latex]1_{\text{four}}[/latex] | [latex]1_{\text{five}}[/latex] | [latex]1_{\text{seven}}[/latex] | [latex]1[/latex] | [latex]1_{\text{twelve}}[/latex] |
| Two | [latex]10_{\text{two}}[/latex] | [latex]2_{\text{four}}[/latex] | [latex]2_{\text{five}}[/latex] | [latex]2_{\text{seven}}[/latex] | [latex]2[/latex] | [latex]2_{\text{twelve}}[/latex] |
| Three | [latex]11_{\text{two}}[/latex] | [latex]3_{\text{four}}[/latex] | [latex]3_{\text{five}}[/latex] | [latex]3_{\text{seven}}[/latex] | [latex]3[/latex] | [latex]3_{\text{twelve}}[/latex] |
| Four | [latex]100_{\text{two}}[/latex] | [latex]10_{\text{four}}[/latex] | [latex]4_{\text{five}}[/latex] | [latex]4_{\text{seven}}[/latex] | [latex]4[/latex] | [latex]4_{\text{twelve}}[/latex] |
| Five | [latex]101_{\text{two}}[/latex] | [latex]11_{\text{four}}[/latex] | [latex]10_{\text{five}}[/latex] | [latex]5_{\text{seven}}[/latex] | [latex]5[/latex] | [latex]5_{\text{twelve}}[/latex] |
| Six | [latex]110_{\text{two}}[/latex] | [latex]12_{\text{four}}[/latex] | [latex]11_{\text{five}}[/latex] | [latex]6_{\text{seven}}[/latex] | [latex]6[/latex] | [latex]6_{\text{twelve}}[/latex] |
| Seven | [latex]111_{\text{two}}[/latex] | [latex]13_{\text{four}}[/latex] | [latex]12_{\text{five}}[/latex] | [latex]10_{\text{seven}}[/latex] | [latex]7[/latex] | [latex]7_{\text{twelve}}[/latex] |
| Eight | [latex]1000_{\text{two}}[/latex] | [latex]20_{\text{four}}[/latex] | [latex]13_{\text{five}}[/latex] | [latex]11_{\text{seven}}[/latex] | [latex]8[/latex] | [latex]8_{\text{twelve}}[/latex] |
| Nine | [latex]1001_{\text{two}}[/latex] | [latex]21_{\text{four}}[/latex] | [latex]14_{\text{five}}[/latex] | [latex]12_{\text{seven}}[/latex] | [latex]9[/latex] | [latex]9_{\text{twelve}}[/latex] |
| Ten | [latex]1010_{\text{two}}[/latex] | [latex]22_{\text{four}}[/latex] | [latex]20_{\text{five}}[/latex] | [latex]13_{\text{seven}}[/latex] | [latex]10[/latex] | [latex]\text{T}_{\text{twelve}}[/latex] |
| Eleven | [latex]1011_{\text{two}}[/latex] | [latex]23_{\text{four}}[/latex] | [latex]21_{\text{five}}[/latex] | [latex]14_{\text{seven}}[/latex] | [latex]11[/latex] | [latex]\text{E}_{\text{twelve}}[/latex] |
| Twelve | [latex]1100_{\text{two}}[/latex] | [latex]30_{\text{four}}[/latex] | [latex]22_{\text{five}}[/latex] | [latex]15_{\text{seven}}[/latex] | [latex]12[/latex] | [latex]10_{\text{twelve}}[/latex] |
| Thirteen | [latex]1101_{\text{two}}[/latex] | [latex]31_{\text{four}}[/latex] | [latex]23_{\text{five}}[/latex] | [latex]16_{\text{seven}}[/latex] | [latex]13[/latex] | [latex]11_{\text{twelve}}[/latex] |
| Fourteen | [latex]1110_{\text{two}}[/latex] | [latex]32_{\text{four}}[/latex] | [latex]24_{\text{five}}[/latex] | [latex]20_{\text{seven}}[/latex] | [latex]14[/latex] | [latex]12_{\text{twelve}}[/latex] |
| Fifteen | [latex]1111_{\text{two}}[/latex] | [latex]33_{\text{four}}[/latex] | [latex]30_{\text{five}}[/latex] | [latex]21_{\text{seven}}[/latex] | [latex]15[/latex] | [latex]13_{\text{twelve}}[/latex] |
Exercise 21
a. What does “10” mean in terms of base blocks?
Solution
It represents one long and zero units.
b. Why is “10” in a different place in each column?
Solution
A long has a different value in each base, so the value of “one long and zero units” changes depending on the base.
c. What is happening in terms of blocks/place value when we count from
- Base ten: 9 to “10”
- Base five: 4 to “10”
- Base twelve: E to “10”
Solution
In each case, we are trading units for a long. In base ten, we need ten units to make a long. So, adding one more unit to 9 units creates ten units, which get traded to make one long. In base five, we need five units to make a long. So, adding one more unit to 4 units creates five units, which get traded to make one long. In base twelve, we need twelve units to make a long. So, adding one more unit to eleven units creates twelve units, which get traded to make one long.
d. Write the expanded form for each numeral in the last row and verify that they are all equal to fifteen.
Solution
Base Two:
[latex](1\times 8)+(1\times 4)+(1\times 2)+(1\times 1)=15[/latex]
Base four:
[latex](3\times 4)+(3\times 1)=15[/latex]
Base five:
[latex](3\times 5)+(0\times 1)=15[/latex]
Base seven:
[latex](2\times 7)+(1\times 1)=15[/latex]
Base ten:
[latex](1\times 10)+(5\times 1)=15[/latex]
Base twelve:
[latex](1\times 12)+(3\times 1)=15[/latex]
Classroom Connection: Geoff asks, “Why do we only have ten symbols for writing out numerals: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9? Why don’t we need more symbols?” What’s your answer?
Solution
As soon as we have ten items in one place value, we trade to create one item in the next place value. So, our numeral never has ten or more in a single place. That is why we only need symbols for 0 through 9.
