9 Module 1.2 Venn Diagrams

Study the Venn diagrams on this and the following pages. It takes a whole lot of practice to shade or identify regions of Venn diagrams. Be advised that it may be necessary to shade several practice diagrams along the way before you get to the final result.
We shade Venn diagrams to represent sets. We will be doing some very easy, basic Venn diagrams as well as several involved and complicated Venn diagrams.
To find the intersection of two sets, you might try shading one region in a given direction and another region in a different direction. Then you would look where those shadings overlap. That overlap would be the intersection.
For example, to visualize A ∩ B, shade A with horizontal lines and B with vertical lines. Then the overlap is A ∩ B. The diagram on the left would be a first step in getting the answer. The shaded part on the diagram to the right shows the final answer.
Here are two problems for you to try. Only shade in the final answer for each exercise.
Exercise 1
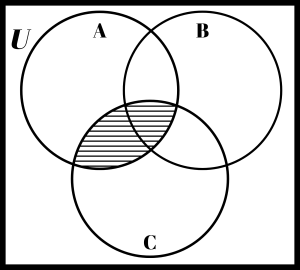
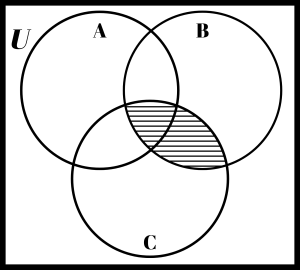
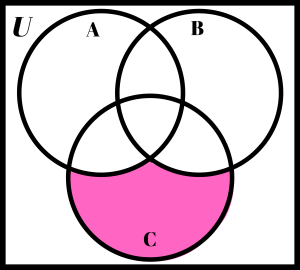
Shade the region that represents A ∩ C

Solution
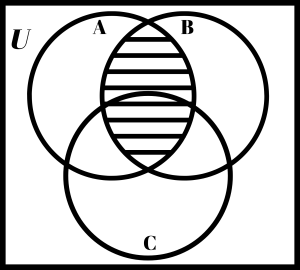
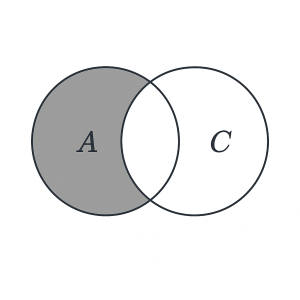
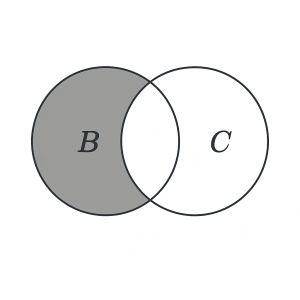
Shade the region that represents B ∩ C

Solution
To shade the union of two sets, shade each region completely, or shade both regions in the same direction. Thus, to find the union of A and B, shade all of A and all of B.
The final answer is represented by the shaded area in the diagram.
Here are two problems for you to try. Only shade in the final answer for each exercise.
Exercise 2
Shade the region that represents A ∪ C

Solution
Shade the region that represents B ∪ C

Solution
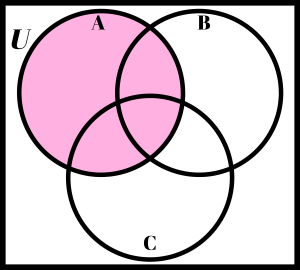
For the complement of a region, shade everything outside the given region. You can think of it as shading everything except that region. On the Venn diagram to the left, the shaded area represents A. On the Venn diagram to the right, the shaded area represents.
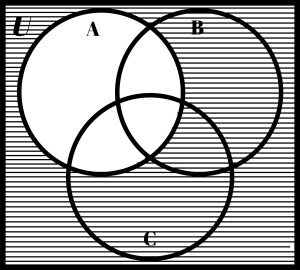
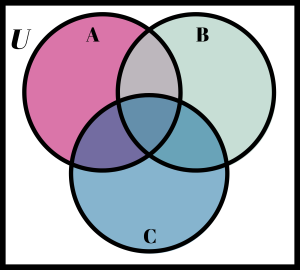
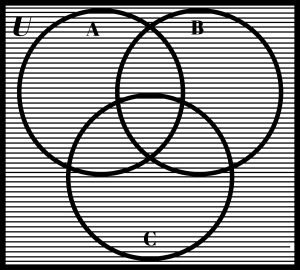
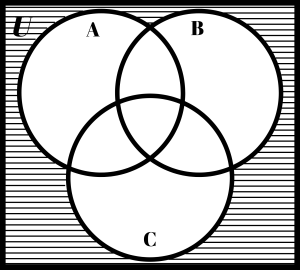
Many people are confused about what part of the Venn diagram represents the universe, U. The universe is the entire Venn diagram, including the sets A, B, and C. The three Venn diagrams on the next page illustrate the differences between U, (A ∪ B ∪ C)c and Uc. Carefully note these differences.
 |
 |
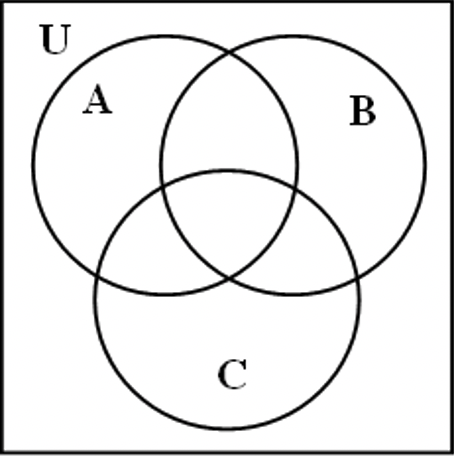 |
| U | (A ∪ B ∪ C)c | Uc |
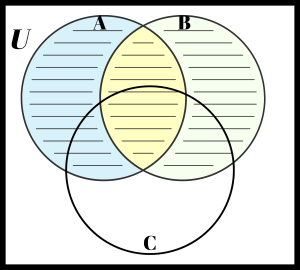
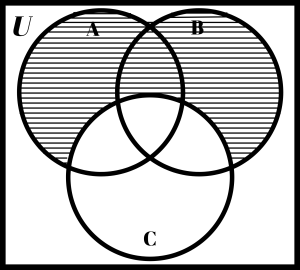
Usually, parentheses are necessary to indicate which operation needs to be done first. If there is only a union or intersection involved, this isn’t necessary, as in (A ∪ B ∪ C)c above. Convince yourself that ((A ∪ B) ∪ C) = (A ∪ (B ∪ C)). Similarly, convince yourself of the analogous fact for intersection by performing the following steps. On the first Venn diagram below, shade A ∩ B with horizontal lines and shade C with vertical lines. Then, the overlap is ((A ∩ B) ∩ C). On the second Venn diagram, shade A with lines slanting to the right and B ∪ C with lines slanting to the left. Then the overlap is (A ∩ (B ∩ C)). Check to see that the final answer, the overlap in this case, is the same for both. Shade the final answer in the third Venn diagram.
Exercise 3
Shade: (A ∩ B) ∩ C

Solution
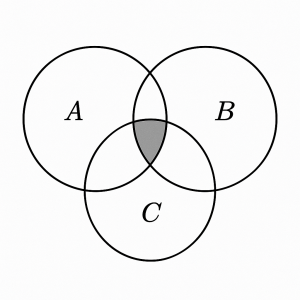
Shade: (A ∩ (B ∩ C))

Solution

Shade final answer here (once you have confirmed that the two diagrams have the same shaded area).

Solution

Now, it’s time for you to try a few more diagrams on your own. It may take more than one step to figure out the answer. You might need to do preliminary drawings on scratch paper first. The shadings you show here should be the final answer only, but you should be able to explain and support how you arrived at your answer. Compare your answers with other people in your class and make sure a consensus is reached on the correct answer. Do this for all the Venn diagrams throughout this exercise set. Shade in the region that represents what is written above each of the six Venn diagrams on the following page. Note that in cases involving more than one operation, it is necessary to use parentheses and follow the order of operations. Exercises 10 and 11 illustrate why this is necessary.
Exercise 4
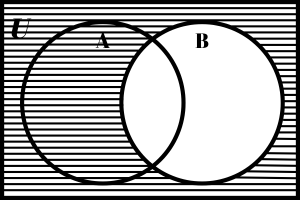
Shade: Bc

Solution
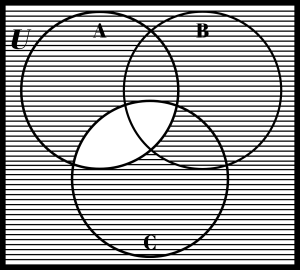
Shade: (C ∩ A)c

Solution
Shade: (B ∪ C)c

Solution

Shade: (A ∩ B ∩ C)c

Solution
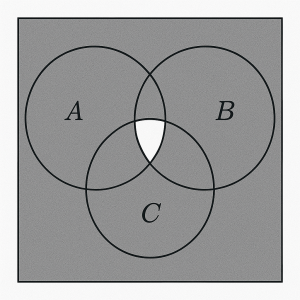
Shade: (A ∩ B) ∪ C

Solution
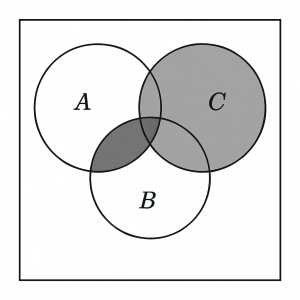
Shade: (A ∩ (B ∪ C))

Solution
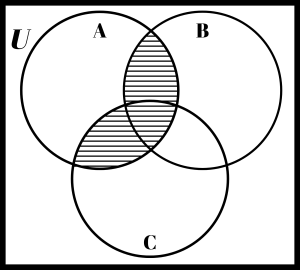
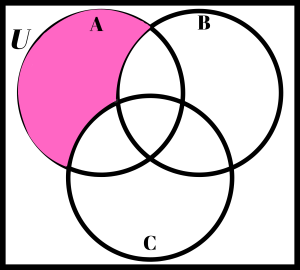
For difference, shade the region coming before the difference sign ( – ) but don’t include or shade any part of the region that follows the difference sign. The Venn on the left represents A–B and the one on the right represents C–A.
 |
 |
Here are two problems for you to try. Only shade in the final answer for each exercise.
Exercise 5
Shade the region that represents A – C

Solution
Shade the region that represents B – C

Solution
Study the following Venn diagrams. Make sure you understand how to get the answers.
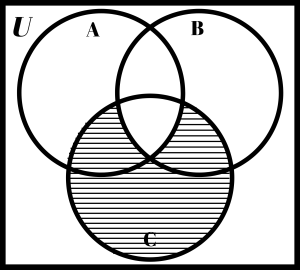
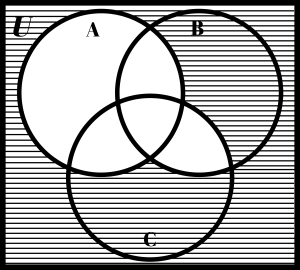
It’s your turn to shade in the region that represents what is written above each diagram.
Exercise 6
Shade: (A ∩ C) – B

Solution
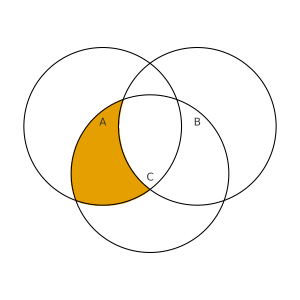
Shade: B – (A ∪ C)

Solution
[Put solution here.]
Shade: (A – C) ∪ (B – A)

Solution
[Put solution here.]
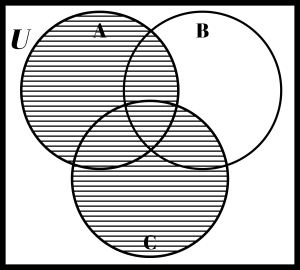
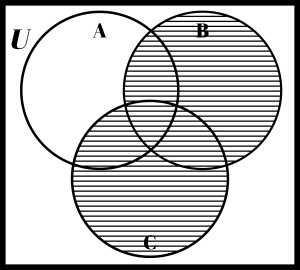
Suppose you wanted to find ((C – A) ∩ B)c. This would probably take a few steps to get the answer. One approach to finding the correct shading is to notice that the final answer is the complement of (C – A) ∩ B. That means we would have to first figure out what (C – A) ∩ B looked like. In order to do that, we notice that this is the intersection of two things C – A and B. On the blank Venn diagram to the left below, shade C – A with horizontal lines and B with vertical lines. The overlap would be the intersection. The overlap on your drawing should match the shading shown on the Venn diagram in the middle. Does it? The last step would then be to take the complement of the shading shown on the middle diagram. This is shown on the Venn diagram on the far right. So, it took drawing three Venn diagrams to come up with the final answer for this problem. Someone else might be able to do it in fewer steps, while someone else might take more steps.
 |
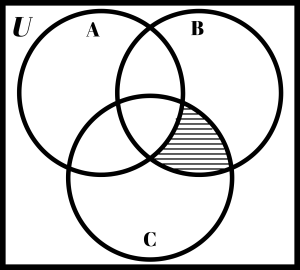 |
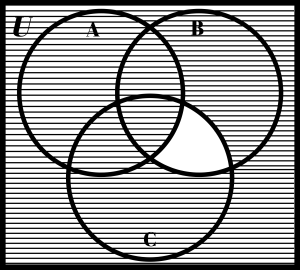 |
| Empty Diagram | (C – A) ∩ B | ((C – A) ∩ B)c |
As mentioned previously, it takes a lot of practice to get good at shading Venn diagrams. It’s even trickier to look at a Venn diagram and describe it, In fact, there is usually more than one way to describe a Venn diagram. For example, the shading for ((C – A) ∩ B)c shown on the previous page is the same as it is for ((C ∩ B) – A)c. What does this mean? We’re so used to only having one correct answer. Well, consider if someone asked you to write an arithmetic problem for which the answer was 2. There would be infinitely many possibilities. For example, 5 – 3 or 1 + 1 or 10/5 would all be acceptable answers. Granted, this kind of question on a test would be harder for a teacher to grade because each student’s response would have to be checked to see if it would work. There isn’t one right answer. The same goes if a teacher asks you to look at a shading of a Venn diagram and describe it. On the other hand, if a description is given and you are asked to shade the Venn diagram, there is only one correct shading. It is much like being asked to compute an arithmetic problem. The answer to 10 – 8 is 2, and that is the only acceptable answer!
The point of all this is that to master the shadings of Venn diagrams and descriptions of Venn diagrams by looking at the shadings takes lots and lots and lots of practice. Give yourself plenty of time to study and work on them, and you will accomplish this feat!!!
On the next few pages, you are asked to shade several one, two, and three set Venn diagrams. The correct shadings follow. Make sure you try these problems in earnest. Make sure you can explain the steps involved to arrive at the correct shading. After mastering the shadings, see if you can look at a shaded Venn diagram and come up with an accurate description. Again, remember there is more than one way to describe a given Venn diagram.
These Venn diagrams will be helpful when studying for a test. Go back and practice drawing the same Venn diagrams later. Use the answers to see if you can describe them by looking at the picture. Of course, remember that your description might not match exactly since there is more than one way to describe any given Venn diagram. If your description is different, make sure you go through the steps of shading a Venn with your description and see if your shading really matches the Venn diagram you were trying to describe.
Here are a few shaded Venn diagrams. See if you can look at the shadings and come up with a description. I’ve put some possible answers at the bottom of this page.
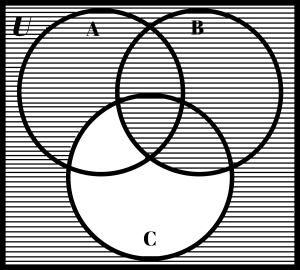 |
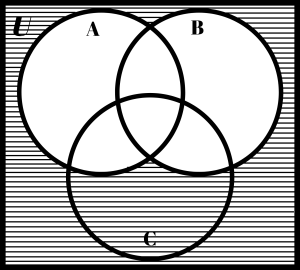 |
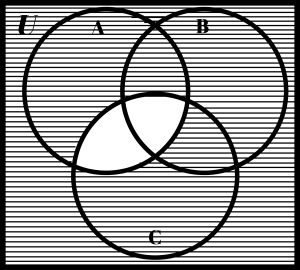 |
Here are some possible descriptions for the above Venn diagrams:
| (C – B)c | (A ∪ C)c | (A ∩ C)c |
Shade the region that represents what is written above each of the one and two set Venn diagrams below. You may need to draw preliminary drawings first for some of them.
Exercise 7
Shade: A

Solution
[Put solution here.]
Shade: Ac

Solution
[Put solution here.]
Shade: U

Solution
[Put solution here.]
Shade: Uc

Solution
[Put solution here.]
Shade: A ∩ B
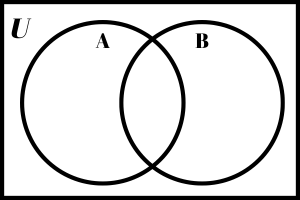
Solution
[Put solution here.]
Shade: A ∪ B

Solution
[Put solution here.]
Shade: A ∪ Bc

Solution
[Put solution here.]
Shade: (A ∩ B)c

Solution
[Put solution here.]
Shade: (A ∪ B)c

Solution
[Put solution here.]
Shade: (A – B) ∪ (B – A)

Solution
[Put solution here.]
Shade: Ac ∪ Bc

Solution
[Put solution here.]
Shade: Ac ∩ Bc

Solution
[Put solution here.]
Shade: (A ∪ B)c ∪ (A ∩ B)

Solution
[Put solution here.]
Shade: B

Solution
[Put solution here.]
Shade: B – A

Solution
[Put solution here.]
Shade: Bc

Solution
[Put solution here.]
Shade the region that represents what is written above each of the one and two set Venn diagrams below. You may need to draw preliminary drawings first for some of them.
Exercise 8
Shade: (A ∩ B) – C

Solution
[Put solution here.]
Shade: (C ∪ B) – A

Solution
[Put solution here.]
Shade: (A ∩ B) ∪ C

Solution
[Put solution here.]
Shade: (A ∪ B) ∩ C

Solution
[Put solution here.]
Shade: Ac – B

Solution
[Put solution here.]
Shade: (A ∩ B ∩ C) – B

Solution
[Put solution here.]
Shade: B – (A ∪ C)

Solution
[Put solution here.]
Shade: C – (A ∩ B)

Solution
[Put solution here.]
Shade: (B – A) ∩ (B – C)

Solution
[Put solution here.]
Shade: (B – A) ∪ (B – C)

Solution
[Put solution here.]
Shade: (A ∪ B)c

Solution
[Put solution here.]
Shade: Ac ∩ Bc

Solution
[Put solution here.]
Shade: Ac – Bc

Solution
[Put solution here.]
Shade: (C – B)c

Solution
[Put solution here.]
Shade: (Bc ∩ C) – A

Solution
[Put solution here.]
Shade: (A – (B ∪ C)) ∪ (B – (A ∪ C)) ∪ (C – (A ∪ B))

Solution
[Put solution here.]
Shade: (A ∩ C)c

Solution
[Put solution here.]
Shade: ((A ∩ B) – C) ∩ (C – A)

Solution
[Put solution here.]
Shade: Ac ∪ Cc

Solution
[Put solution here.]
Shade: B ∩ (C ∪ Ac)

Solution
[Put solution here.]
In the Material Card section there are blank Venn diagram templates you can use for practice.
