3.5 Composition of Functions
Cynthia Singleton; Ginny Bradley; Karen Perilloux; and Prakash Ghimire
Learning Objectives
In this section, you will:
- Identify the degree and leading coefficient of polynomials.
- Add and subtract polynomials.
- Multiply polynomials.
- Perform operations with polynomials of several variables.
- Combine functions using algebraic operations.
- Create a new function by composition of functions.
- Evaluate composite functions.
- Find the domain of a composite function.
- Decompose a composite function into its component functions.
Earl is building a doghouse, whose front is in the shape of a square topped with a triangle. There will be a rectangular door through which the dog can enter and exit the house. Earl wants to find the area of the front of the doghouse so that he can purchase the correct amount of paint. Using the measurements of the front of the house, shown in Figure 1, we can create an expression that combines several variable terms, allowing us to solve this problem and others like it.
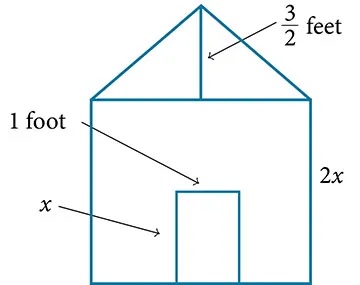
First find the area of the square in square feet.
[latex]A = s^2 = (2x)^2 = 4x^2[/latex]
Then find the area of the triangle in square feet.
[latex]A=\frac{1}{2}bh = \frac{1}{2}(2x)\left( \frac{3}{2} \right)= \frac{3}{2}x[/latex]
Next find the area of the rectangular door in square feet.
[latex]A = lw = x \cdot 1 = x[/latex]
The area of the front of the doghouse can be found by adding the areas of the square and the triangle and then subtracting the area of the rectangle. When we do this, we get [latex]4x^2 + \frac{3}{2}x - x \ \text{ft}^2[/latex] or [latex]4x^2 + \frac{1}{2}x \ \text{ft}^2[/latex].
In this section, we will examine expressions such as this one, which combine several variable terms.
Identifying the Degree and Leading Coefficient of Polynomials
The formula just found is an example of a polynomial, which is a sum of or difference of terms, each consisting of a variable raised to a nonnegative integer power. A number multiplied by a variable raised to an exponent, such as [latex]384 \pi ,[/latex] is known as a coefficient. Coefficients can be positive, negative, or zero and can be whole numbers, decimals, or fractions. Each product [latex]{a}_{i}{x}^{i},[/latex] such as [latex]384 \pi w,[/latex] is a term of a polynomial. If a term does not contain a variable, it is called a constant.
A polynomial containing only one term, such as [latex]5{x}^{4},[/latex] is called a monomial. A polynomial containing two terms, such as [latex]2x-9,[/latex] is called a binomial. A polynomial containing three terms, such as [latex]-3{x}^{2}+8x-7,[/latex] is called a trinomial.
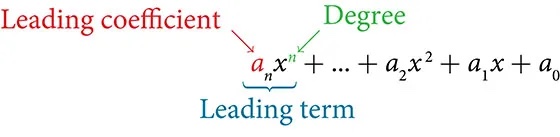
We can find the degree of a polynomial by identifying the highest power of the variable that occurs in the polynomial. The term with the highest degree is called the leading term because it is usually written first. The coefficient of the leading term is called the leading coefficient. When a polynomial is written so that the powers are descending, we say that it is in standard form.
Polynomials
A polynomial is an expression that can be written in the form
Each real number ai is called a coefficient. The number [latex]{a}_{0},[/latex]that is not multiplied by a variable is called a constant. Each product [latex]{a}_{i}{x}^{i},[/latex]is a term of a polynomial. The highest power of the variable that occurs in the polynomial is called the degree of a polynomial. The leading term is the term with the highest power, and its coefficient is called the leading coefficient.
How To
Given a polynomial expression, identify the degree and leading coefficient.
- Find the highest power of x to determine the degree.
- Identify the term containing the highest power of x to find the leading term.
- Identify the coefficient of the leading term.
Identifying the Degree and Leading Coefficient of a Polynomial
For the following polynomials, identify the degree, the leading term, and the leading coefficient.
- [latex]3+2{x}^{2}-4{x}^{3}[/latex]
- [latex]5{t}^{5}-2{t}^{3}+7t[/latex]
- [latex]6p-{p}^{3}-2[/latex]
Show Solution
- The highest power of x is 3, so the degree is 3. The leading term is the term containing that degree, [latex]-4{x}^{3}.[/latex]The leading coefficient is the coefficient of that term, [latex]-4.[/latex]
- The highest power of t is [latex]5,[/latex] so the degree is [latex]5.[/latex]The leading term is the term containing that degree, [latex]5{t}^{5}.[/latex]The leading coefficient is the coefficient of that term, [latex]5.[/latex]
- The highest power of p is [latex]3,[/latex] so the degree is [latex]3.[/latex]The leading term is the term containing that degree, [latex]-{p}^{3}.[/latex] The leading coefficient is the coefficient of that term, [latex]-1.[/latex]
Try It
Identify the degree, leading term, and leading coefficient of the polynomial [latex]4{x}^{2}-{x}^{6}+2x-6.[/latex]
Show Solution
The degree is 6, the leading term is[latex]-{x}^{6},[/latex] and the leading coefficient is [latex]-1.[/latex]
Adding and Subtracting Polynomials
We can add and subtract polynomials by combining like terms, which are terms that contain the same variables raised to the same exponents. For example, [latex]5{x}^{2 }[/latex] and [latex]-2{x}^{2}[/latex] are like terms and can be added to get [latex]3{x}^{2}[/latex], but [latex]3x[/latex] and [latex]3{x}^{2}[/latex] are not like terms and therefore cannot be added.
https://www.youtube.com/watch?v=MKZRotdEjy8
How To
Given multiple polynomials, add or subtract them to simplify the expressions.
- Combine like terms.
- Simplify and write in standard form.
Adding Polynomials
Find the sum.
[latex](12{x}^{2}+9x-21)+(4{x}^{3}+8{x}^{2}-5x+20)[/latex]
Show Solution
| = [latex]4x^{3}+ (12x^{2} + 8x^{2}) + (9x - 5x) + (-21 + 20)[/latex] | Combine like terms. |
| = [latex]4x^{3} + 20x^{2} + 4x - 1[/latex] | Simplify. |
Analysis
We can check our answers to these types of problems using a graphing calculator. To check, graph the problem as given along with the simplified answer. The two graphs should be equivalent. Be sure to use the same window to compare the graphs. Using different windows can make the expressions seem equivalent when they are not.
Try It
Find the sum.
[latex](2{x}^{3}+5{x}^{2}-x+1)+(2{x}^{2}-3x-4)[/latex]
Show Solution
[latex]2{x}^{3}+7{x}^{2}-4x-3[/latex]
Subtracting Polynomials
Find the difference.
[latex](7{x}^{4}-{x}^{2}+6x+1)-(5{x}^{3}-2{x}^{2}+3x+2)[/latex]
Show Solution
| [latex]7{x}^{4}-5{x}^{3}+(-{x}^{2}+2{x}^{2})+(6x - 3x)+(1 - 2)[/latex] | Combine like terms. |
| [latex]7{x}^{4}-5{x}^{3}+{x}^{2}+3{x}-1[/latex] | Simplify. |
Analysis
Note that finding the difference between two polynomials is the same as adding the opposite of the second polynomial to the first.
Try It
Find the difference.
[latex](-7{x}^{3}-7{x}^{2}+6x-2)-(4{x}^{3}-6{x}^{2}-x+7)[/latex]
Show Solution
[latex]-11{x}^{3}-{x}^{2}+7x-9[/latex]
Multiplying Polynomials
Multiplying polynomials is a bit more challenging than adding and subtracting polynomials. We must use the distributive property to multiply each term in the first polynomial by each term in the second polynomial. We then combine like terms. We can also use a shortcut called the FOIL method when multiplying binomials. Certain special products follow patterns that we can memorize and use instead of multiplying the polynomials by hand each time. We will look at a variety of ways to multiply polynomials.
Multiplying Polynomials Using the Distributive Property
To multiply a number by a polynomial, we use the distributive property. The number must be distributed to each term of the polynomial. We can distribute the [latex]2[/latex] in [latex]2(x+7)[/latex] to obtain the equivalent expression [latex]2x+14.[/latex] When multiplying polynomials, the distributive property allows us to multiply each term of the first polynomial by each term of the second. We then add the products together and combine like terms to simplify.
How To
Given the multiplication of two polynomials, use the distributive property to simplify the expression.
- Multiply each term of the first polynomial by each term of the second.
- Combine like terms.
- Simplify.
Multiplying Polynomials Using the Distributive Property
Find the product.
[latex](2x+1)(3{x}^{2}-x+4)[/latex]
Show Solution
| [latex]2x(3x^2 - x + 4) + 1(3x^2 - x + 4)[/latex] | Use distributive property |
| [latex](6x^3 - 2x^2 + 8x) + (3x^2 - x + 4)[/latex] | Multiply |
| [latex]6x^3 + (-2x^2 + 3x^2) + (8x - x) + 4[/latex] | Combine like terms |
| [latex]6x^3 + x^2 + 7x + 4[/latex] | Simplify |
Analysis
We can use a table to keep track of our work, as shown in the table below. Write one polynomial across the top and the other down the side. For each box in the table, multiply the term for that row by the term for that column. Then add all of the terms together, combine like terms, and simplify.
| [latex]3{x}^{2}[/latex] | [latex]-x[/latex] | [latex]+4[/latex] | |
| [latex]2x[/latex] | [latex]6{x}^{3}[/latex] | [latex]-2{x}^{2}[/latex] | [latex]8x[/latex] |
| [latex]+1[/latex] | [latex]3{x}^{2}[/latex] | [latex]-x[/latex] | [latex]4[/latex] |
Try It
Find the product.
[latex](3x+2)({x}^{3}-4{x}^{2}+7)[/latex]
Show Solution
[latex]3{x}^{4}-10{x}^{3}-8{x}^{2}+21x+14[/latex]
Using FOIL to Multiply Binomials
A shortcut called FOIL is sometimes used to find the product of two binomials. It is called FOIL because we multiply the first terms, the outer terms, the inner terms, and then the last terms of each binomial.

The FOIL method arises out of the distributive property. We are simply multiplying each term of the first binomial by each term of the second binomial and then combining like terms.
How To
Given two binomials, use FOIL to simplify the expression.
- Multiply the first terms of each binomial.
- Multiply the outer terms of the binomials.
- Multiply the inner terms of the binomials.
- Multiply the last terms of each binomial.
- Add the products.
- Combine like terms and simplify.
Using FOIL to Multiply Binomials
Use FOIL to find the product.
[latex](2x-18)(3x+3)[/latex]
Show Solution
Find the product of the first terms.

Find the product of the outer terms.

Find the product of the inner terms.

Find the product of the last terms.

| [latex]6x^2 + 6x - 54x - 54 \qquad \text{Add the products} \\[/latex] |
| [latex]6x^2 + (6x - 54x) - 54 \quad \text{Combine like terms} \\[/latex] |
| [latex]6x^2 - 48x - 54 \qquad \qquad \text{Simplify}[/latex] |
Try It
Use FOIL to find the product.
[latex](x+7)(3x-5)[/latex]
Show Solution
[latex]3{x}^{2}+16x-35[/latex]
Perfect Square Trinomials
Certain binomial products have special forms. When a binomial is squared, the result is called a perfect square trinomial. We can find the square by multiplying the binomial by itself. However, there is a special form that each of these perfect square trinomials takes, and memorizing the form makes squaring binomials much easier and faster. Let’s look at a few perfect square trinomials to familiarize ourselves with the form.
[latex](x + 5)^2 = x^2 + 10x + 25[/latex]
[latex](x - 3)^2 = x^2 - 6x + 9[/latex]
[latex](4x - 1)^2 = 16x^2 - 8x + 1[/latex]
Notice that the first term of each trinomial is the square of the first term of the binomial, and similarly, the last term of each trinomial is the square of the last term of the binomial. The middle term is double the product of the two terms. Lastly, we see that the first sign of the trinomial is the same as the sign of the binomial.
https://www.youtube.com/watch?v=SlRgONK-DXA
Perfect Square Trinomials
When a binomial is squared, the result is the first term squared added to double the product of both terms and the last term squared.
How To
Given a binomial, square it using the formula for perfect square trinomials.
- Square the first term of the binomial.
- Square the last term of the binomial.
- For the middle term of the trinomial, double the product of the two terms.
- Add and simplify.
Expanding Perfect Squares
Expand [latex]{(3x-8)}^{2}.[/latex]
Show Solution
Begin by squaring the first term and the last term. For the middle term of the trinomial, double the product of the two terms.
Then simplify
Try It
Expand [latex]{(4x-1)}^{2}.[/latex]
Show Solution
[latex]16{x}^{2}-8x+1[/latex]
Difference of Squares
Another special product is called the difference of squares, which occurs when we multiply a binomial by another binomial with the same terms but the opposite sign. Let’s see what happens when we multiply [latex](x+1)(x-1),[/latex]using the FOIL method.
The middle term drops out, resulting in a difference of squares. Just as we did with the perfect squares, let’s look at a few examples.
[latex](x+11)(x-11) = x^2 - 121[/latex]
[latex](2x+3)(2x-3) = 4x^2 - 9[/latex]
Because the sign changes in the second binomial, the outer and inner terms cancel each other out, and we are left only with the square of the first term minus the square of the last term.
Q&A
Is there a special form for the sum of squares?
No. The difference of squares occurs because the opposite signs of the binomials cause the middle terms to disappear. There are no two binomials that multiply to equal a sum of squares.
Difference of Squares
When a binomial is multiplied by a binomial with the same terms separated by the opposite sign, the result is the square of the first term minus the square of the last term.
How To
Given a binomial multiplied by a binomial with the same terms but the opposite sign, find the difference of squares.
- Square the first term of the binomials.
- Square the last term of the binomials.
- Subtract the square of the last term from the square of the first term.
Multiplying Binomials Resulting in a Difference of Squares
Multiply[latex](9x+4)(9x-4).[/latex]
Show Solution
Square the first term to get [latex]{(9x)}^{2}=81{x}^{2}.[/latex]Square the last term to get [latex]{4}^{2}=16.[/latex]Subtract the square of the last term from the square of the first term to find the product of [latex]81{x}^{2}-16.[/latex]
Try It
Multiply[latex](2x+7)(2x-7).[/latex]
Show Solution
[latex]4{x}^{2}-49[/latex]
Performing Operations with Polynomials of Several Variables
We have looked at polynomials containing only one variable. However, a polynomial can contain several variables. All of the same rules apply when working with polynomials containing several variables. Consider an example:
| [latex](a + 2b)(4a - b - c) =[/latex] | Use the distributive property |
| [latex]= a(4a - b - c) + 2b(4a - b - c)[/latex] | Multiply |
| [latex]= 4a^2 - ab - ac + 8ab - 2b^2 - 2bc[/latex] | Combine like terms |
| [latex]= 4a^2 + (-ab + 8ab) - ac - 2b^2 - 2bc[/latex] | Simplify |
| [latex]= 4a^2 + 7ab - ac - 2bc - 2b^2[/latex] |
Multiplying Polynomials Containing Several Variables
Multiply [latex](x+4)(3x-2y+5).[/latex]
Show Solution
Follow the same steps that we used to multiply polynomials containing only one variable.
| [latex]x(3x - 2y + 5) + 4(3x - 2y + 5)=[/latex] | Use the distributive property |
| [latex]= 3x^2 - 2xy + 5x + 12x - 8y + 20[/latex] | Multiply |
| [latex]= 3x^2 - 2xy + (5x + 12x) - 8y + 20[/latex] | Combine like terms |
| [latex]= 3x^2 - 2xy + 17x - 8y + 20[/latex] | Simplify |
Try It
Multiply [latex](3x-1)(2x+7y-9).[/latex]
Show Solution
[latex]6{x}^{2}+21xy-29x-7y+9[/latex]
Combining Functions Using Algebraic Operations
Suppose we want to calculate how much it costs to heat a house on a particular day of the year. The cost to heat a house will depend on the average daily temperature, and in turn, the average daily temperature depends on the particular day of the year. Notice how we have just defined two relationships: The cost depends on the temperature, and the temperature depends on the day.
Using descriptive variables, we can notate these two functions. The function [latex]C(T)[/latex] gives the cost [latex]C[/latex] of heating a house for a given average daily temperature in [latex]T[/latex] degrees Celsius. The function [latex]T(d)[/latex] gives the average daily temperature on day [latex]d[/latex] of the year. For any given day, [latex]\text{Cost}=C(T(d))[/latex] means that the cost depends on the temperature, which in turn depends on the day of the year. Thus, we can evaluate the cost function at the temperature [latex]T(d).[/latex] For example, we could evaluate [latex]T(5)[/latex] to determine the average daily temperature on the 5th day of the year. Then, we could evaluate the cost function at that temperature. We would write [latex]C(T(5)).[/latex]
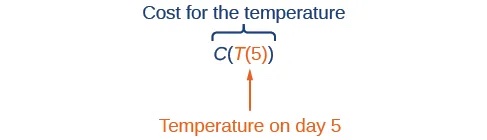
By combining these two relationships into one function, we have performed function composition, which is the focus of this section.
Function composition is only one way to combine existing functions. Another way is to carry out the usual algebraic operations on functions, such as addition, subtraction, multiplication, and division. We do this by performing the operations with the function outputs, defining the result as the output of our new function.
Suppose we need to add two columns of numbers that represent a husband and wife’s separate annual incomes over a period of years, with the result being their total household income. We want to do this for every year, adding only that year’s income and then collecting all the data in a new column. If [latex]w(y)[/latex] is the wife’s income and [latex]h(y)[/latex] is the husband’s income in a year [latex]y[/latex] and we want [latex]T[/latex] to represent the total income, then we can define a new function.
If this holds true for every year, then we can focus on the relation between the functions without reference to a year and write
Just as for this sum of two functions, we can define difference, product, and ratio functions for any pair of functions that have the same kinds of inputs (not necessarily numbers) and also the same kinds of outputs (which do have to be numbers so that the usual operations of algebra can apply to them, and which also must have the same units or no units when we add and subtract). In this way, we can think of adding, subtracting, multiplying, and dividing functions.
For two functions [latex]f(x),[/latex] and [latex]g(x)[/latex] with real number outputs, we define new functions [latex]f+g,f-g,fg,[/latex] and [latex]\frac{f}{g}[/latex] by the relations
[latex](f + g)(x) = f(x) + g(x) [/latex]
[latex](f - g)(x) = f(x) - g(x) [/latex]
[latex](fg)(x) = f(x)g(x) [/latex]
[latex]\left(\frac{f}{g}\right)(x) = \frac{f(x)}{g(x)} \quad \text{where } g(x) \ne 0[/latex]
Performing Algebraic Operations on Functions
Find and simplify the functions [latex](g-f)(x)[/latex] and [latex](\frac{g}{f})(x)[/latex] given [latex]f(x)=x-1[/latex] and [latex]g(x)={x}^{2}-1.[/latex] Are they the same function?
Show Solution
Begin by writing the general form, and then substitute the given functions.
[latex](g - f)(x) = g(x) - f(x) [/latex]
[latex](g - f)(x) = x^2 - 1 - (x - 1) [/latex]
[latex]= x^2 - x [/latex]
[latex]= x(x - 1) [/latex]
[latex]\left(\frac{g}{f}\right)(x) = \frac{g(x)}{f(x)} [/latex]
[latex]\left(\frac{g}{f}\right)(x) = \frac{x^2 - 1}{x - 1} [/latex]
[latex]= \frac{(x + 1)(x - 1)}{x - 1} \quad \text{where } x \ne 1 [/latex]
[latex]= x + 1[/latex]
No, the functions are not the same.
Note: For [latex](\frac{g}{f})(x)[/latex] the condition [latex],x \ne 1,[/latex] is necessary because when [latex]x=1[/latex] the denominator is equal to [latex]0[/latex], which makes the function undefined.
Try It
Find and simplify the functions[latex](fg)(x)[/latex] and [latex](f-g)(x)[/latex] given [latex]f(x)=x-1 [/latex] and [latex]g(x)={x}^{2}-1[/latex]. Are they the same function?
Show Solution
[latex](fg)(x) = f(x)g(x) = (x - 1)(x^2 - 1) = x^3 - x^2 - x + 1 [/latex]
[latex](f - g)(x) = f(x) - g(x) = (x - 1) - (x^2 - 1) = x - x^2[/latex]
No, the functions are not the same.
Create a Function by Composition of Functions
Performing algebraic operations on functions combines them into a new function, but we can also create functions by composing functions. When we wanted to compute a heating cost from a day of the year, we created a new function that takes a day as input and yields a cost as output. The process of combining functions so that the output of one function becomes the input of another is known as a composition of functions. The resulting function is known as a composite function. We represent this combination by the following notation:
We read the left-hand side as “[latex]f[/latex] composed with [latex]g[/latex] at [latex]x[/latex]” and the right-hand side as “[latex]f[/latex] of [latex]g[/latex] of [latex]x.[/latex]” The two sides of the equation have the same mathematical meaning and are equal. The open circle symbol [latex]\circ ,[/latex] is called the composition operator. We use this operator mainly when we wish to emphasize the relationship between the functions themselves without referring to any particular input value. Composition is a binary operation that takes two functions and forms a new function, much as addition or multiplication takes two numbers and gives a new number. However, it is important not to confuse function composition with multiplication because, as we learned above, in most cases [latex]f(g(x)) \ne f(x)g(x).[/latex]
It is also important to understand the order of operations in evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first and then working to the outside. In the equation above, the function [latex]g[/latex] takes the input [latex]x[/latex] first and yields an output [latex]g(x).[/latex] Then the function[latex]f[/latex] takes [latex]g(x)[/latex] as an input and yields an output [latex]f(g(x)).[/latex]

In general,[latex]f \circ g[/latex] and [latex]g \circ f[/latex] are different functions. In other words, in many cases [latex]f(g(x)) \ne g(f(x))[/latex] for all [latex]x.[/latex] We will also see that sometimes two functions can be composed only in one specific order.
For example, if [latex]f(x)={x}^{2}[/latex] and [latex]g(x)=x+2,[/latex] then
[latex]f(g(x)) = f(x + 2) [/latex]
[latex]= (x + 2)^2 [/latex]
[latex]= x^2 + 4x + 4[/latex]
but
[latex]g(f(x)) = g(x^2) [/latex]
[latex]= x^2 + 2[/latex]
These expressions are not equal for all values of [latex]x[/latex] so the two functions are not equal. It is irrelevant that the expressions happen to be equal for the single input value [latex]x=\frac{1}{2}.[/latex]
Note that the range of the inside function (the first function to be evaluated) needs to be within the domain of the outside function. Less formally, the composition has to make sense in terms of inputs and outputs.
Composition of Functions
When the output of one function is used as the input of another, we call the entire operation a composition of functions. For any input [latex]x[/latex] and functions [latex]f[/latex] and [latex]g[/latex] this action defines a composite function, which we write as [latex]f \circ g[/latex] such that
The domain of the composite function [latex]f \circ g[/latex] is all [latex]x[/latex] such that [latex]x[/latex] is in the domain of [latex]g[/latex] and [latex]g(x)[/latex] is in the domain of [latex]f.[/latex]
It is important to realize that the product of functions [latex]fg[/latex] is not the same as the function composition [latex]f(g(x))[/latex] because, in general, [latex]f(x)g(x) \ne f(g(x)).[/latex]
Determining Whether Composition of Functions Is Commutative
Given [latex]f(x) = 2x + 1[/latex] and [latex]g(x) = 3 - x[/latex], find [latex]f(g(x))[/latex] and [latex]g(f(x)).[/latex] Determine whether the composition of the functions is commutative.
Show Solution
Let’s begin by substituting [latex]g(x)[/latex] into [latex]f(x).[/latex]
[latex]= 6 - 2x + 1 [/latex]
[latex]= 7 - 2x[/latex]
Now we can substitute [latex]f(x)[/latex] into [latex]g(x).[/latex]
[latex]= 3 - 2x - 1 [/latex]
[latex]= -2x + 2[/latex]
We find that [latex]g(f(x)) \ne f(g(x))[/latex], so the operation of function composition is not commutative.
Interpreting Composite Functions
The function [latex]c(s)[/latex] gives the number of calories burned completing [latex]s[/latex] sit-ups, and [latex]s(t),[/latex] gives the number of sit-ups a person can complete in [latex]t[/latex] minutes. Interpret [latex]c(s(3)).[/latex]
Show Solution
The inside expression in the composition is [latex]s(3).[/latex] Because the input to the s-function is time,[latex]t=3[/latex] represents 3 minutes, and [latex]s(3)[/latex] is the number of sit-ups completed in 3 minutes.
Using [latex]s(3)[/latex] as the input to the function [latex]c(s)[/latex] gives us the number of calories burned during the number of sit-ups that can be completed in 3 minutes, or simply the number of calories burned in 3 minutes (by doing sit-ups).
Investigating the Order of Function Composition
Suppose [latex]f(x)[/latex] gives miles that can be driven in [latex]x[/latex] hours and [latex]g(y)[/latex] gives the gallons of gas used in driving [latex]y[/latex] miles. Which of these expressions is meaningful:[latex]f(g(y))[/latex] or [latex]g(f(x))?[/latex]
Show Solution
The function [latex]y=f(x)[/latex]is a function whose output is the number of miles driven corresponding to the number of hours driven.
The function [latex]g(y)[/latex] is a function whose output is the number of gallons used corresponding to the number of miles driven. This means:
The expression [latex]g(y)[/latex] takes miles as the input and a number of gallons as the output. The function [latex]f(x)[/latex] requires a number of hours as the input. Trying to input a number of gallons does not make sense. The expression [latex]f(g(y))[/latex] is meaningless.
The expression [latex]f(x)[/latex] takes hours as input and the number of miles driven as the output. The function [latex]g(y)[/latex] requires a number of miles as the input. Using [latex]f(x)[/latex] (miles driven) as an input value for [latex]g(y)[/latex] where gallons of gas depend on miles driven, does make sense. The expression [latex]g(f(x))[/latex]makes sense and will yield the number of gallons of gas used, [latex]g[/latex] driving a certain number of miles, [latex]f(x)[/latex] in [latex]x[/latex] hours.
Q&A
Are there any situations where[latex]f(g(y))[/latex] and [latex]g(f(x))[/latex] would both be meaningful or useful expressions?
Yes. For many pure mathematical functions, both compositions make sense, even though they usually produce different new functions. In real-world problems, functions whose inputs and outputs have the same units also may give compositions that are meaningful in either order.
Try It
The gravitational force on a planet at a distance r from the sun is given by the function [latex]G(r).[/latex] The acceleration of a planet subjected to any force [latex]F[/latex] is given by the function [latex]a(F).[/latex] Form a meaningful composition of these two functions, and explain what it means.
Show Solution
A gravitational force is still a force, so [latex]a(G(r))[/latex] makes sense as the acceleration of a planet at a distance r from the Sun (due to gravity), but [latex]G(a(F))[/latex] does not make sense.
Evaluating Composite Functions
Once we compose a new function from two existing functions, we need to be able to evaluate it for any input in its domain. We will do this with specific numerical inputs for functions expressed as tables, graphs, and formulas and with variables as inputs to functions expressed as formulas. In each case, we evaluate the inner function using the starting input and then use the inner function’s output as the input for the outer function.
Evaluating Composite Functions Using Tables
When working with functions given as tables, we read input and output values from the table entries and always work from the inside to the outside. We evaluate the inside function first and then use the output of the inside function as the input to the outside function.
Using a Table to Evaluate a Composite Function
Using Table 1, evaluate [latex]f(g(3)),[/latex] and [latex]g(f(3)).[/latex]
| [latex]x[/latex] | [latex]f(x)[/latex] | [latex]g(x)[/latex] |
|---|---|---|
| 1 | 6 | 3 |
| 2 | 8 | 5 |
| 3 | 3 | 2 |
| 4 | 1 | 7 |
Show Solution
To evaluate [latex]f(g(3))[/latex], we start from the inside with the input value 3. We then evaluate the inside expression [latex]g(3)[/latex] using the table that defines the function [latex]g: g(3)=2.[/latex] We can then use that result as the input to the function [latex]f[/latex] so [latex]g(3)[/latex] is replaced by 2 and we get [latex]f(2).[/latex] Then, using the table that defines the function [latex]f[/latex] we find that [latex]f(2)=8.[/latex]
[latex]f(g(3)) = f(2) = 8[/latex]
To evaluate [latex]g(f(3))[/latex], we first evaluate the inside expression[latex]f(3)[/latex] using the first table:[latex]f(3)=3.[/latex] Then, using the table for [latex]g[/latex] we can evaluate
Table 2 shows the composite functions [latex]f \circ g[/latex] and [latex]g \circ f[/latex] as tables.
| [latex]x[/latex] | [latex]g(x)[/latex] | [latex]f(g(x))[/latex] | [latex]f(x)[/latex] | [latex]g(f(x))[/latex] |
| 3 | 2 | 8 | 3 | 2 |
Try It
Using Table 1, evaluate [latex]f(g(1))[/latex] and [latex]g(f(4)).[/latex]
Show Solution
[latex]f(g(1))=f(3)=3[/latex] and [latex]g(f(4))=g(1)=3[/latex]
Evaluating Composite Functions Using Graphs
When we are given individual functions as graphs, the procedure for evaluating composite functions is similar to the process we use for evaluating tables. We read the input and output values, but this time, from the [latex]x \text{-}[/latex] and [latex]y \text{- axes}[/latex] of the graphs.
How To
Given a composite function and graphs of its individual functions, evaluate it using the information provided by the graphs.
- Locate the given input to the inner function on the [latex],x \text{-axis }[/latex] of its graph.
- Read off the output of the inner function from the [latex],y \text{-axis }[/latex] of its graph.
- Locate the inner function output on the [latex],x \text{-axis }[/latex] of the graph of the outer function.
- Read the output of the outer function from the [latex],y \text{-axis }[/latex] of its graph. This is the output of the composite function.
Using a Graph to Evaluate a Composite Function
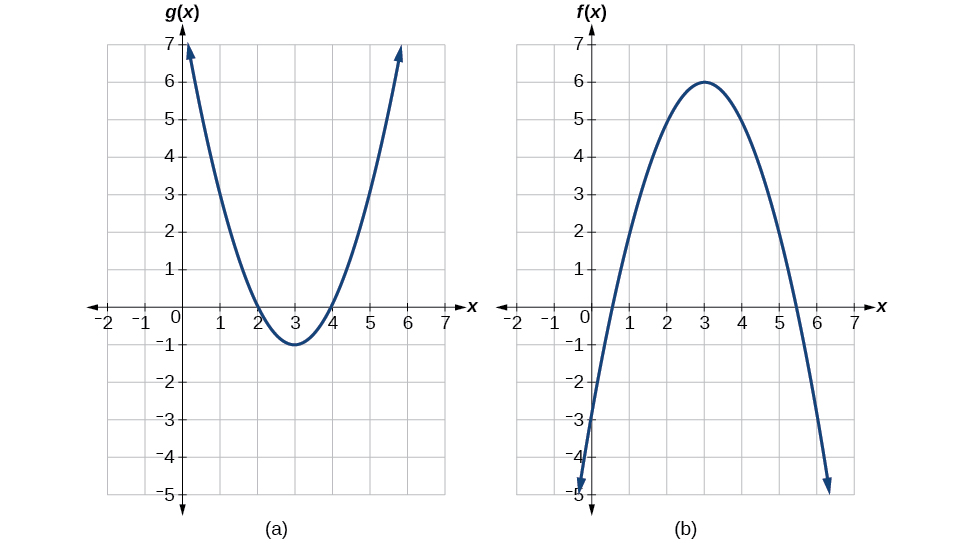
Using Figure 1, evaluate [latex]f(g(1)).[/latex]
Show Solution
To evaluate [latex]f(g(1))[/latex] we start with the inside evaluation. See Figure 2.
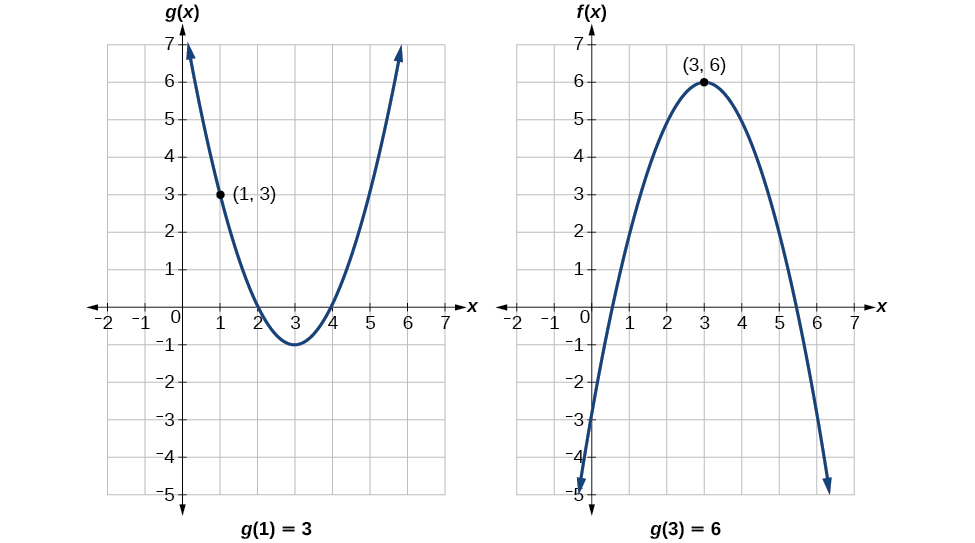
We evaluate [latex]g(1)[/latex] using the graph of [latex]g(x)[/latex], finding the input of 1 on the x-axis and finding the output value of the graph at that input. Here, [latex]g(1)=3.[/latex] We use this value as the input to the function[latex]f.[/latex]
[latex]f(g(1))=f(3)[/latex]
We can then evaluate the composite function by looking at the graph of [latex]f(x)[/latex], finding the input of 3 on the x-axis and reading the output value of the graph at this input. Here, [latex]f(3)=6[/latex] so [latex]f(g(1))=6.[/latex]
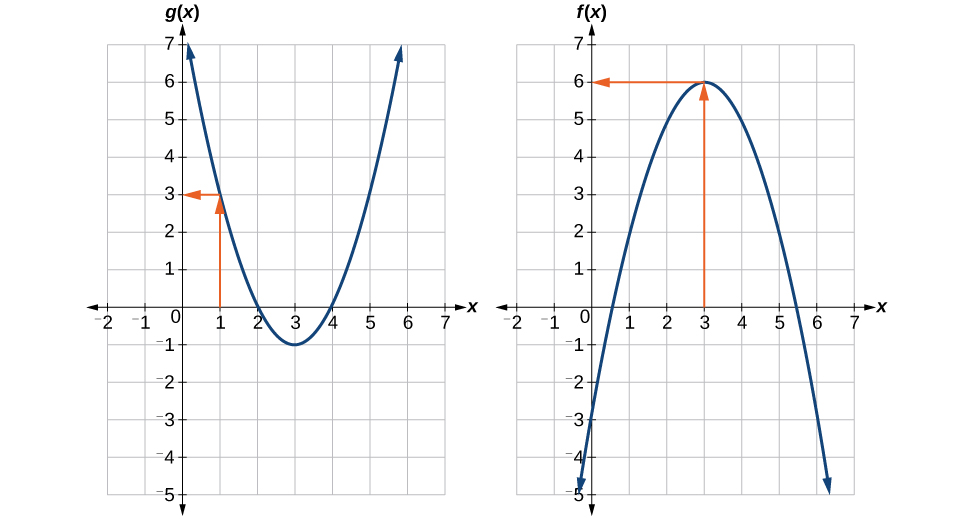
Analysis
Figure 3 shows how we can mark the graphs with arrows to trace the path from the input value to the output value.
Try It
Using Figure 1, evaluate [latex]g(f(2)).[/latex]
Show Solution
[latex]g(f(2))=g(5)=3[/latex]
bookmark search for ],
Evaluating Composite Functions Using Formulas
When evaluating a composite function where we have either created or been given formulas, the rule of working from the inside out remains the same. The input value to the outer function will be the output of the inner function, which may be a numerical value, a variable name, or a more complicated expression.
While we can compose the functions for each individual input value, it is sometimes helpful to find a single formula that will calculate the result of a composition [latex]f(g(x)).[/latex] To do this, we will extend our idea of function evaluation. Recall that when we evaluate a function like [latex]f(t)={t}^{2}-t[/latex], we substitute the value inside the parentheses into the formula wherever we see the input variable.
How To
Given a formula for a composite function, evaluate the function.
- Evaluate the inside function using the input value or variable provided.
- Use the resulting output as the input to the outside function.
Evaluating a Composition of Functions Expressed as Formulas with a Numerical Input
Given [latex]f(t)={t}^{2}-t,[/latex] and [latex]h(x)=3x+2[/latex] evaluate [latex]f(h(1)).[/latex]
Show Solution
Because the inside expression is [latex]h(1)[/latex] we start by evaluating [latex]h(x),[/latex] at 1.
[latex]h(1) = 5[/latex]
Then [latex]f(h(1))=f(5)[/latex] so we evaluate [latex]f(t)[/latex] at an input of 5.
[latex]f(h(1))= 5^2 - 5[/latex]
[latex]f(h(1))= 20[/latex]
Analysis
It makes no difference what the input variables [latex],t,[/latex] and [latex],x,[/latex] were called in this problem because we evaluated for specific numerical values.
Try It
Given [latex]f(t)={t}^{2}-t[/latex] and [latex]h(x)=3x+2[/latex] evaluate
- [latex]h(f(2))[/latex]
- [latex]h(f(-2))[/latex]
Show Solution
a. 8
b. 20
Finding the Domain of a Composite Function
As we discussed previously, the domain of a composite function such as [latex]f \circ g[/latex] is dependent on the domain of [latex],g,[/latex] and the domain of [latex],f.[/latex] It is important to know when we can apply a composite function and when we cannot—that is, to know the domain of a function such as [latex],f \circ g.[/latex] Let us assume we know the domains of the functions [latex],f,[/latex]and[latex],g,[/latex] separately. If we write the composite function for an input [latex],x,[/latex] as [latex]f(g(x))[/latex] we can see right away that [latex]x[/latex] must be a member of the domain of [latex]g[/latex] in order for the expression to be meaningful because otherwise, we cannot complete the inner function evaluation. However, we also see that [latex]g(x)[/latex] must be a member of the domain of [latex]f[/latex]; otherwise, the second function evaluation in [latex]f(g(x))[/latex] cannot be completed, and the expression is still undefined. Thus the domain of [latex]f \circ g[/latex] consists of only those inputs in the domain of [latex]g[/latex] that produce outputs from [latex]g[/latex] belonging to the domain of [latex]f.[/latex] Note that the domain of [latex]f[/latex] composed with [latex]g[/latex] is the set of all [latex]x[/latex] such that [latex]x[/latex] is in the domain of [latex]g[/latex] and [latex]g(x)[/latex] is in the domain of [latex]f.[/latex]
Domain of a Composite Function
The domain of a composite function[latex]f(g(x))[/latex] is the set of those inputs [latex]x[/latex] in the domain of [latex]g[/latex] for which [latex]g(x)[/latex] is in the domain of[latex]f.[/latex]
How To
Given a function composition[latex]f(g(x))[/latex] determine its domain.
- Find the domain of[latex]g.[/latex]
- Find the domain of[latex]f.[/latex]
- Find those inputs [latex]x[/latex] in the domain of [latex]g[/latex] for which [latex]g(x)[/latex] is in the domain of [latex]f.[/latex] That is, exclude those inputs [latex]x[/latex] from the domain of [latex]g[/latex] for which [latex]g(x)[/latex] is not in the domain of [latex]f.[/latex] The resulting set is the domain of [latex]f \circ g.[/latex]
Finding the Domain of a Composite Function
Find the domain of [latex](f \circ g)(x)\text{ where }f(x)=frac{5}{x-1} \text{ and }g(x)=\frac{4}{3x-2}[/latex]
Show Solution
The domain of [latex]g(x)[/latex] consists of all real numbers except [latex],x=\frac{2}{3},,[/latex] since that input value would cause us to divide by 0. Likewise, the domain of [latex],f,[/latex] consists of all real numbers except 1. So we need to exclude from the domain of [latex]g(x)[/latex]that value of[latex]x[/latex]for which[latex]g(x)=1.[/latex]
[latex]4 = 3x - 2 [/latex]
[latex]6 = 3x [/latex]
[latex]x = 2[/latex]
So the domain of [latex],fcirc g,[/latex] is the set of all real numbers except [latex],frac{2}{3},[/latex] and [latex],2.[/latex] This means that
We can write this in interval notation as
Finding the Domain of a Composite Function Involving Radicals
Find the domain of [latex](f \circ g)(x) \text{ where},,,,,,f(x)=\sqrt{x+2} \text{ and }g(x)= \sqrt{3-x}[/latex]
Show Solution
Because we cannot take the square root of a negative number, the domain of [latex]g[/latex] is [latex](-infty ,3].[/latex] Now we check the domain of the composite function
For [latex](f \circ g)(x)= \sqrt{\sqrt{3-x}+2} \sqrt{3-x}+2 \ge 0[/latex] since the radicand of a square root must be positive. Since square roots are positive, [latex]\text{}\sqrt{3-x}\ge 0,\text{}[/latex] or, [latex]3-x \ge 0, \text{}[/latex] which gives a domain of [latex](-infty ,3][/latex].
Analysis
This example shows that knowledge of the range of functions (specifically the inner function) can also be helpful in finding the domain of a composite function. It also shows that the domain of [latex],fcirc g,[/latex] can contain values that are not in the domain of [latex],f,,[/latex] though they must be in the domain of [latex],g.[/latex]
Try It
Find the domain of [latex](f \circ g)(x) \text{ where }f(x)=\frac{1}{x-2}\text{ and }g(x)=\sqrt{x+4}[/latex]
Show Solution
[latex][-4,0)\cup (0,infty )[/latex]
Decomposing a Composite Function into its Component Functions
In some cases, it is necessary to decompose a complicated function. In other words, we can write it as a composition of two simpler functions. There may be more than one way to decompose a composite function, so we may choose the decomposition that appears to be most expedient.
Decomposing a Function
Write [latex]f(x)=\sqrt{5-{x}^{2}}[/latex] as the composition of two functions.
Show Solution
We are looking for two functions, [latex],g,[/latex] and [latex],h,[/latex] so [latex]f(x)=g(h(x)).[/latex] To do this, we look for a function inside a function in the formula for [latex]f(x).[/latex] As one possibility, we might notice that the expression [latex],5-{x}^{2},[/latex] is the inside of the square root. We could then decompose the function as
We can check our answer by recomposing the functions.
Try It
Write [latex]f(x)=\frac{4}{3-sqrt{4+{x}^{2}}}[/latex] as the composition of two functions.
Show Solution
Possible answer:
[latex]g(x) = \sqrt{4 + x^2} [/latex]
[latex]h(x) = \frac{4}{3 - x} [/latex]
[latex]f = h \circ g[/latex]
Key Equation
| Composite function | [latex](f\circ g)(x)=f(g(x))[/latex] |
Key Equations
| perfect square trinomial | [latex]{(x+a)}^{2}=(x+a)(x+a)={x}^{2}+2ax+{a}^{2}[/latex] |
| difference of squares | [latex](a+b)(a-b)={a}^{2}-{b}^{2}[/latex] |
| Composite function | [latex](f \circ g)(x)=f(g(x))[/latex] |
Key Concepts
- A polynomial is a sum of terms each consisting of a variable raised to a non-negative integer power. The degree is the highest power of the variable that occurs in the polynomial. The leading term is the term containing the highest degree, and the leading coefficient is the coefficient of that term.
- We can add and subtract polynomials by combining like terms.
- To multiply polynomials, use the distributive property to multiply each term in the first polynomial by each term in the second. Then add the products.
- FOIL (First, Outer, Inner, Last) is a shortcut that can be used to multiply binomials.
- Perfect square trinomials and difference of squares are special products. .
- Follow the same rules to work with polynomials containing several variables.
- We can perform algebraic operations on functions.
- When functions are combined, the output of the first (inner) function becomes the input of the second (outer) function.
- The function produced by combining two functions is a composite function.
- The order of function composition must be considered when interpreting the meaning of composite functions.
- A composite function can be evaluated by evaluating the inner function using the given input value and then evaluating the outer function taking as its input the output of the inner function.
- A composite function can be evaluated from a table.
- A composite function can be evaluated from a graph.
- A composite function can be evaluated from a formula.
- The domain of a composite function consists of those inputs in the domain of the inner function that correspond to outputs of the inner function that are in the domain of the outer function.
- Just as functions can be combined to form a composite function, composite functions can be decomposed into simpler functions.
- Functions can often be decomposed in more than one way.
Section Exercises
Verbal
- Evaluate the following statement: The degree of a polynomial in standard form is the exponent of the leading term. Explain why the statement is true or false.
Show Solution
The statement is true. In standard form, the polynomial with the highest value exponent is placed first and is the leading term. The degree of a polynomial is the value of the highest exponent, which in standard form is also the exponent of the leading term.
- Many times, multiplying two binomials with two variables results in a trinomial. This is not the case when there is a difference of two squares. Explain why the product in this case is also a binomial.
- You can multiply polynomials with any number of terms and any number of variables using four basic steps over and over until you reach the expanded polynomial. What are the four steps?
Show Solution
Use the distributive property, multiply, combine like terms, and simplify.
- State whether the following statement is true, and explain why or why not: A trinomial is always a higher degree than a monomial.
Algebraic
For the following exercises, identify the degree of the polynomial.
- [latex]7x-2{x}^{2}+13[/latex]
Show Solution
2
- [latex]14{m}^{3}+{m}^{2}-16m+8[/latex]
- [latex]-625{a}^{8}+16{b}^{4}[/latex]
Show Solution
8
- [latex]200p-30{p}^{2}m+40{m}^{3}[/latex]
- [latex]{x}^{2}+4x+4[/latex]
Show Solution
2
- [latex]6{y}^{4}-{y}^{5}+3y-4[/latex]
For the following exercises, find the sum or difference.
- [latex](12{x}^{2}+3x)-(8{x}^{2}-19)[/latex]
Show Solution
[latex]4{x}^{2}+3x+19[/latex]
- [latex](4{z}^{3}+8{z}^{2}-z)+(-2{z}^{2}+z+6)[/latex]
- [latex](6{w}^{2}+24w+24)-(3w{}^{2}-6w+3)[/latex]
Show Solution
[latex]3{w}^{2}+30w+21[/latex]
- [latex](7{a}^{3}+6{a}^{2}-4a-13)+(-3{a}^{3}-4{a}^{2}+6a+17)[/latex]
- [latex](11{b}^{4}-6{b}^{3}+18{b}^{2}-4b+8)-(3{b}^{3}+6{b}^{2}+3)[/latex]
Show Solution
[latex]11{b}^{4}-9{b}^{3}+12{b}^{2}-7b+8[/latex]
- [latex](49{p}^{2}-25)+(16{p}^{4}-32{p}^{2}+16)[/latex]
For the following exercises, find the product.
- [latex](4x+2)(6x-4)[/latex]
Show Solution
[latex]24{x}^{2}-4x-8[/latex]
- [latex](14{c}^{2}+4c)(2{c}^{2}-3c)[/latex]
- [latex](6{b}^{2}-6)(4{b}^{2}-4)[/latex]
Show Solution
[latex]24{b}^{4}-48{b}^{2}+24[/latex]
- [latex](3d-5)(2d+9)[/latex]
- [latex](9v-11)(11v-9)[/latex]
Show Solution
[latex]99{v}^{2}-202v+99[/latex]
- [latex](4{t}^{2}+7)(-3{t}^{2}+4)[/latex]
- [latex](8n-4r)({n}^{2}+9)[/latex]
Show Solution
[latex]8{n}^{3}-4{n}^{2}+72n-36[/latex]
For the following exercises, expand the binomial.
- [latex]{left(4x+5right)}^{2}[/latex]
- [latex]{left(3y-7right)}^{2}[/latex]
Show Solution
[latex]9{y}^{2}-42y+49[/latex]
- [latex]{left(12-4xright)}^{2}[/latex]
- [latex]{left(4p+9right)}^{2}[/latex]
Show Solution
[latex]16{p}^{2}+72p+81[/latex]
- [latex]{left(2m-3right)}^{2}[/latex]
- [latex]{left(3y-6right)}^{2}[/latex]
Show Solution
[latex]9{y}^{2}-36y+36[/latex]
- [latex]{left(9b+1right)}^{2}[/latex]
For the following exercises, multiply the binomials.
- [latex]left(4c+1right)left(4c-1right)[/latex]
Show Solution
[latex]16{c}^{2}-1[/latex]
- [latex]left(9a-4right)left(9a+4right)[/latex]
- [latex]left(15n-6right)left(15n+6right)[/latex]
Show Solution
[latex]225{n}^{2}-36[/latex]
- [latex]left(25b+2right)left(25b-2right)[/latex]
- [latex]left(4+4mright)left(4-4mright)[/latex]
Show Solution
[latex]-16{m}^{2}+16[/latex]
- [latex]left(14p+7right)left(14p-7right)[/latex]
- [latex]left(11q-10right)left(11q+10right)[/latex]
Show Solution
[latex]121{q}^{2}-100[/latex]
For the following exercises, multiply the polynomials.
- [latex]left(2{x}^{2}+2x+1right)left(4x-1right)[/latex]
- [latex]left(4{t}^{2}+t-7right)left(4{t}^{2}-1right)[/latex]
Show Solution
[latex]16{t}^{4}+4{t}^{3}-32{t}^{2}-t+7[/latex]
- [latex]left(x-1right)left({x}^{2}-2x+1right)[/latex]
- [latex]left(y-2right)left({y}^{2}-4y-9right)[/latex]
Show Solution
[latex]{y}^{3}-6{y}^{2}-y+18[/latex]
- [latex]left(6k-5right)left(6{k}^{2}+5k-1right)[/latex]
- [latex]left(3{p}^{2}+2p-10right)left(p-1right)[/latex]
Show Solution
[latex]3{p}^{3}-{p}^{2}-12p+10[/latex]
- [latex]left(4m-13right)left(2{m}^{2}-7m+9right)[/latex]
- [latex]left(a+bright)left(a-bright)[/latex]
Show Solution
[latex]{a}^{2}-{b}^{2}[/latex]
- [latex]left(4x-6yright)left(6x-4yright)[/latex]
- [latex]{left(4t-5uright)}^{2}[/latex]
Show Solution
[latex]16{t}^{2}-40tu+25{u}^{2}[/latex]
- [latex]left(9m+4n-1right)left(2m+8right)[/latex]
- [latex]left(4t-xright)left(t-x+1right)[/latex]
Show Solution
[latex]4{t}^{2}+{x}^{2}+4t-5tx-x[/latex]
- [latex]left({b}^{2}-1right)left({a}^{2}+2ab+{b}^{2}right)[/latex]
- [latex]left(4r-dright)left(6r+7dright)[/latex]
Show Solution
[latex]24{r}^{2}+22rd-7{d}^{2}[/latex]
- [latex]left(x+yright)left({x}^{2}-xy+{y}^{2}right)[/latex]
Real-World Applications
- A developer wants to purchase a plot of land to build a house. The area of the plot can be described by the following expression:[latex],left(4x+1right)left(8x-3right),[/latex], where x is measured in meters. Multiply the binomials to find the area of the plot in standard form.
Show Solution
[latex]32{x}^{2}-4x-3,[/latex]m2
- A prospective buyer wants to know how much grain a specific silo can hold. The area of the floor of the silo is[latex],{left(2x+9right)}^{2}.[/latex]The height of the silo is[latex],10x+10,[/latex]where x is measured in feet. Expand the square and multiply by the height to find the expression that shows how much grain the silo can hold.
Extensions
For the following exercises, perform the given operations.
- [latex]{left(4t-7right)}^{2}left(2t+1right)-left(4{t}^{2}+2t+11right)[/latex]
Show Solution
[latex]32{t}^{3}-100{t}^{2}+40t+38[/latex]
- [latex]left(3b+6right)left(3b-6right)left(9{b}^{2}-36right)[/latex]
- [latex]left({a}^{2}+4ac+4{c}^{2}right)left({a}^{2}-4{c}^{2}right)[/latex]
Show Solution
[latex]{a}^{4}+4{a}^{3}c-16a{c}^{3}-16{c}^{4}[/latex]
Verbal
- How does one find the domain of the quotient of two functions,[latex],frac{f}{g}?,[/latex]
Show Solution
Find the numbers that make the function in the denominator [latex],g,[/latex] equal to zero, and check for any other domain restrictions on [latex],f,[/latex] and [latex],g,,[/latex] such as an even-indexed root or zeros in the denominator.
- What is the composition of two functions,[latex],fcirc g?[/latex]
- If the order is reversed when composing two functions, can the result ever be the same as the answer in the original order of the composition? If yes, give an example. If no, explain why not.
Show Solution
Yes. Sample answer: Let[latex],fleft(xright)=x+1text{ and }gleft(xright)=x-1.[/latex]Then[latex],fleft(gleft(xright)right)=fleft(x-1right)=left(x-1right)+1=x,[/latex]and[latex],gleft(fleft(xright)right)=gleft(x+1right)=left(x+1right)-1=x.[/latex]So[latex],fcirc g=gcirc f.[/latex]
- How do you find the domain for the composition of two functions,[latex],fcirc g?[/latex]
Algebraic
For the following exercises, determine the domain for each function in interval notation.
- Given[latex],fleft(xright)={x}^{2}+2xtext{ }[/latex]and[latex]gleft(xright)=6-{x}^{2},[/latex]find[latex],f+g,,f-g,,fg,text{ }[/latex]and[latex]text{ },frac{f}{g}.[/latex]
Show Solution
[latex]left(f+gright)left(xright)=2x+6,,[/latex]domain:[latex],left(-infty ,infty right)[/latex]
[latex]left(f-gright)left(xright)=2{x}^{2}+2x-6,,[/latex]domain:[latex],left(-infty ,infty right)[/latex]
[latex]left(fgright)left(xright)=-{x}^{4}-2{x}^{3}+6{x}^{2}+12x,,[/latex]domain:[latex],left(-infty ,infty right)[/latex]
[latex]left(frac{f}{g}right)left(xright)=frac{{x}^{2}+2x}{6-{x}^{2}},,[/latex]domain:[latex],left(-infty ,-sqrt{6}right)cup left(-sqrt{6},sqrt{6}right)cup left(sqrt{6},infty right)[/latex]
- Given[latex],fleft(xright)=-3{x}^{2}+xtext{ }[/latex]and[latex]text{ }gleft(xright)=5,,[/latex]find[latex],f+g,,f-g,,fg,,[/latex]and[latex]text{ },frac{f}{g}.[/latex]
- Given[latex],fleft(xright)=2{x}^{2}+4xtext{ }[/latex]and[latex]text{ }gleft(xright)=frac{1}{2x},[/latex]find[latex],f+g,,f-g,,fg,text{ }[/latex]and[latex]text{ }frac{f}{g}.[/latex]
Show Solution
[latex]left(f+gright)left(xright)=frac{4{x}^{3}+8{x}^{2}+1}{2x},,[/latex]domain:[latex],left(-infty ,0right)cup left(0,infty right)[/latex]
[latex]left(f-gright)left(xright)=frac{4{x}^{3}+8{x}^{2}-1}{2x},,[/latex]domain:[latex],left(-infty ,0right)cup left(0,infty right)[/latex]
[latex]left(fgright)left(xright)=x+2,,[/latex]domain:[latex],left(-infty ,0right)cup left(0,infty right)[/latex]
[latex]left(frac{f}{g}right)left(xright)=4{x}^{3}+8{x}^{2},,[/latex]domain:[latex],left(-infty ,0right)cup left(0,infty right)[/latex]
- Given[latex],fleft(xright)=frac{1}{x-4},[/latex]and[latex],gleft(xright)=frac{1}{6-x},,[/latex]find[latex],f+g,,f-g,,fg,text{ }[/latex]and[latex]text{ }frac{f}{g}.[/latex]
- Given [latex],fleft(xright)=3{x}^{2},[/latex]and[latex],gleft(xright)=sqrt{x-5},,[/latex]find[latex],f+g,,f-g,,fg,text{ }[/latex]and[latex]text{ }frac{f}{g}.[/latex]
Show Solution
[latex]left(f+gright)left(xright)=3{x}^{2}+sqrt{x-5},,[/latex]domain:[latex],left[5,infty right)[/latex]
[latex]left(f-gright)left(xright)=3{x}^{2}-sqrt{x-5},,[/latex]domain:[latex],left[5,infty right)[/latex]
[latex]left(fgright)left(xright)=3{x}^{2}sqrt{x-5},,[/latex]domain:[latex],left[5,infty right)[/latex]
[latex]left(frac{f}{g}right)left(xright)=frac{3{x}^{2}}{sqrt{x-5}},,[/latex]domain:[latex],left(5,infty right)[/latex]
- Given[latex],fleft(xright)=sqrt{x},[/latex]and[latex],gleft(xright)=|x-3|,,[/latex]find[latex],frac{g}{f}.[/latex]
- For the following exercise, find the indicated function given[latex],fleft(xright)=2{x}^{2}+1,[/latex]and[latex],gleft(xright)=3x-5.[/latex]
- [latex]fleft(gleft(2right)right)[/latex]
- [latex]fleft(gleft(xright)right)[/latex]
- [latex]gleft(fleft(xright)right)[/latex]
- [latex]left(gcirc gright)left(xright)[/latex]
- [latex]left(fcirc fright)left(-2right)[/latex]
Show Solution
a. 3; b.[latex],fleft(gleft(xright)right)=2{left(3x-5right)}^{2}+1;,[/latex]c.[latex],fleft(gleft(xright)right)=6{x}^{2}-2;,[/latex]d.[latex],left(gcirc gright)left(xright)=3left(3x-5right)-5=9x-20;,[/latex]e.[latex],left(fcirc fright)left(-2right)=163[/latex]
For the following exercises, use each pair of functions to find[latex],fleft(gleft(xright)right),[/latex]and[latex],gleft(fleft(xright)right).[/latex]Simplify your answers.
- [latex]fleft(xright)={x}^{2}+1,,gleft(xright)=sqrt{x+2}[/latex]
- [latex]fleft(xright)=sqrt{x}+2,,gleft(xright)={x}^{2}+3[/latex]
Show Solution
[latex]fleft(gleft(xright)right)=sqrt{{x}^{2}+3}+2,,gleft(fleft(xright)right)=x+4sqrt{x}+7[/latex]
- [latex]fleft(xright)=|x|,,gleft(xright)=5x+1[/latex]
- [latex]fleft(xright)=sqrt[3]{x},,gleft(xright)=frac{x+1}{{x}^{3}}[/latex]
Show Solution
[latex]fleft(gleft(xright)right)=sqrt[3]{frac{x+1}{{x}^{3}}}=frac{sqrt[3]{x+1}}{x},,gleft(fleft(xright)right)=frac{sqrt[3]{x}+1}{x}[/latex]
- [latex]f(x)=\frac{1}{x-6} \quad g(x)=\frac{7}{x}+6[/latex]
- [latex]f(x)=\frac{1}{x-4} \quad g(x)=\frac{2}{x}+4[/latex]
Show Solution
[latex](f\circ g)(x)=\frac{1}{\frac{2}{x}+4-4}=\frac{x}{2} \text{ }(g \circ f)(x)=2x-4[/latex]
For the following exercises, use each set of functions to find[latex]f(g(h(x))).[/latex]Simplify your answers.
- [latex]f(x)={x}^{4}+6[/latex][latex]g(x)=x-6[/latex] and [latex]h(x)=\sqrt{x}[/latex]
- [latex]f(x)={x}^{2}+1[/latex], [latex]g(x)=\frac{1}{x}[/latex], and [latex]h(x)=x+3[/latex]
Show Solution
[latex]fleft(gleft(hleft(xright)right)right)={left(frac{1}{x+3}right)}^{2}+1[/latex]
- Given[latex],fleft(xright)=frac{1}{x},[/latex]and[latex],gleft(xright)=x-3,,[/latex]find the following:
- [latex]left(fcirc gright)left(xright)[/latex]
- the domain of[latex],left(fcirc gright)left(xright),[/latex]in interval notation
- [latex]left(gcirc fright)left(xright)[/latex]
- the domain of[latex],left(gcirc fright)left(xright),[/latex]
- [latex]left(frac{f}{g}right)x[/latex]
- Given[latex],fleft(xright)=sqrt{2-4x},[/latex]and[latex],gleft(xright)=-frac{3}{x},,[/latex]find the following:
- [latex]left(gcirc fright)left(xright)[/latex]
- the domain of[latex],left(gcirc fright)left(xright),[/latex]in interval notation
Show Solution
a.[latex],left(gcirc fright)left(xright)=-frac{3}{sqrt{2-4x}};,[/latex]
b.[latex],left(-infty ,frac{1}{2}right)[/latex]
- Given the functions[latex],fleft(xright)=frac{1-x}{x},,text{and},,gleft(xright)=frac{1}{1+{x}^{2}},[/latex] find the following:
- [latex]left(gcirc fright)left(xright)[/latex]
- [latex]left(gcirc fright)left(text{2}right)[/latex]
- Given functions[latex],pleft(xright)=frac{1}{sqrt{x}},[/latex]and[latex],mleft(xright)={x}^{2}-4,,[/latex]state the domain of each of the following functions using interval notation:
- [latex]frac{pleft(xright)}{mleft(xright)}[/latex]
- [latex]pleft(mleft(xright)right)[/latex]
- [latex]mleft(pleft(xright)right)[/latex]
Show Solution
a.[latex],left(0,2right)cup left(2,infty right);,[/latex]b.[latex],left(-infty ,-2right)cup left(2,infty right);,[/latex]c.[latex],left(0,infty right)[/latex]
- Given functions[latex],qleft(xright)=frac{1}{sqrt{x}},[/latex]and[latex],hleft(xright)={x}^{2}-9,,[/latex]state the domain of each of the following functions using interval notation.
- [latex]frac{qleft(xright)}{hleft(xright)}[/latex]
- [latex]qleft(hleft(xright)right)[/latex]
- [latex]hleft(qleft(xright)right)[/latex]
- For[latex],fleft(xright)=frac{1}{x},[/latex]and[latex],gleft(xright)=sqrt{x-1},,[/latex]write the domain of[latex],left(fcirc gright)left(xright),[/latex]in interval notation.
Show Solution
[latex]left(1,infty right)[/latex]
For the following exercises, find functions[latex],fleft(xright),[/latex]and[latex],gleft(xright),[/latex]so the given function can be expressed as[latex],hleft(xright)=fleft(gleft(xright)right).[/latex]
- [latex]hleft(xright)={left(x+2right)}^{2}[/latex]
- [latex]hleft(xright)={left(x-5right)}^{3}[/latex]
Show Solution
sample: [latex]f(x) = x^3 \quad g(x) = x - 5[/latex]
- [latex]hleft(xright)=frac{3}{x-5}[/latex]
- [latex]hleft(xright)=frac{4}{{left(x+2right)}^{2}}[/latex]
Show Solution
sample: [latex]f(x) = \frac{4}{x} \quad g(x) = (x + 2)^2[/latex]
- [latex]hleft(xright)=4+sqrt[3]{x}[/latex]
- [latex]hleft(xright)=sqrt[3]{frac{1}{2x-3}}[/latex]
Show Solution
sample: [latex]f(x) = \sqrt[3]{x} \quad g(x) = \frac{1}{2x - 3}[/latex]
- [latex]hleft(xright)=frac{1}{{left(3{x}^{2}-4right)}^{-3}}[/latex]
- [latex]hleft(xright)=sqrt[4]{frac{3x-2}{x+5}}[/latex]
Show Solution
sample: [latex]f(x) = \sqrt[4]{x} \quad g(x) = \frac{3x - 2}{x + 5}[/latex]
- [latex]hleft(xright)={left(frac{8+{x}^{3}}{8-{x}^{3}}right)}^{4}[/latex]
- [latex]hleft(xright)=sqrt{2x+6}[/latex]
Show Solution
sample: [latex]f(x) = \sqrt{x} \quad g(x) = 2x + 6[/latex]
- [latex]hleft(xright)={left(5x-1right)}^{3}[/latex]
- [latex]hleft(xright)=sqrt[3]{x-1}[/latex]
Show Solution
sample: [latex]f(x) = \sqrt[3]{x} \quad g(x) = x - 1[/latex]
- [latex]hleft(xright)=|{x}^{2}+7|[/latex]
- [latex]hleft(xright)=frac{1}{{left(x-2right)}^{3}}[/latex]
Show Solution
sample: [latex]f(x) = x^3 \quad g(x) = \frac{1}{x - 2}[/latex]
- [latex]hleft(xright)={left(frac{1}{2x-3}right)}^{2}[/latex]
- [latex]hleft(xright)=sqrt{frac{2x-1}{3x+4}}[/latex]
Show Solution
sample: [latex]f(x) = \sqrt{x} \quad g(x) = \frac{2x - 1}{3x + 4}[/latex]
Graphical
For the following exercises, use the graphs of[latex],f,[/latex] shown in Figure 4 and [latex],g,[/latex] shown in Figure 5, to evaluate the expressions.
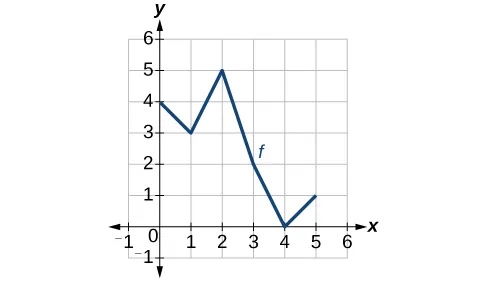
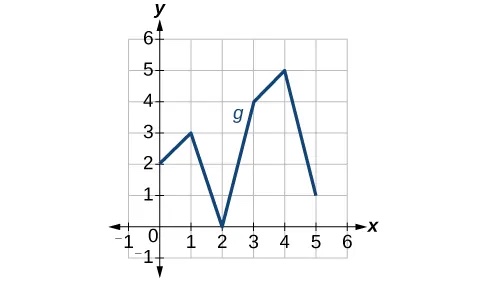
- [latex]fleft(gleft(3right)right)[/latex]
- [latex]fleft(gleft(1right)right)[/latex]
Show Solution
2
- [latex]gleft(fleft(1right)right)[/latex]
- [latex]gleft(fleft(0right)right)[/latex]
Show Solution
5
- [latex]fleft(fleft(5right)right)[/latex]
- [latex]fleft(fleft(4right)right)[/latex]
Show Solution
4
- [latex]gleft(gleft(2right)right)[/latex]
- [latex]gleft(gleft(0right)right)[/latex]
Show Solution
0
For the following exercises, use graphs of [latex],fleft(xright),[/latex] shown in Figure 6,[latex],gleft(xright),[/latex] shown in Figure 7, and[latex],hleft(xright),[/latex] shown in Figure 8 below, to evaluate the expressions.
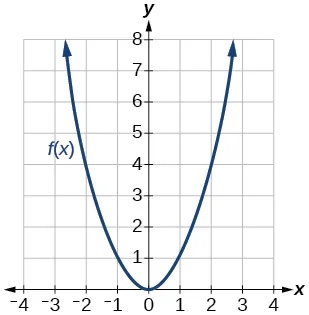
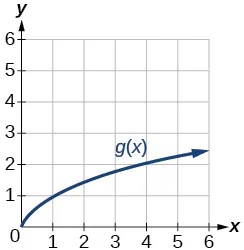
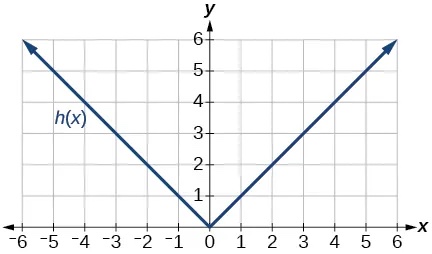
- [latex]gleft(fleft(1right)right)[/latex]
- [latex]gleft(fleft(2right)right)[/latex]
Show Solution
2
- [latex]fleft(gleft(4right)right)[/latex]
- [latex]fleft(gleft(1right)right)[/latex]
Show Solution
1
- [latex]fleft(hleft(2right)right)[/latex]
- [latex]hleft(fleft(2right)right)[/latex]
Show Solution
4
- [latex]fleft(gleft(hleft(4right)right)right)[/latex]
- [latex]fleft(gleft(fleft(-2right)right)right)[/latex]
Show Solution
4
Numeric
For the following exercises, use the function values for[latex],ftext{ and }g,[/latex]shown in Table 3 to evaluate each expression.
| [latex]x[/latex] | [latex]f(x)[/latex] | [latex]g(x)[/latex] |
|---|---|---|
| 0 | 7 | 9 |
| 1 | 6 | 5 |
| 2 | 5 | 6 |
| 3 | 8 | 2 |
| 4 | 4 | 1 |
| 5 | 0 | 8 |
| 6 | 2 | 7 |
| 7 | 1 | 3 |
| 8 | 9 | 4 |
| 9 | 3 | 0 |
- [latex]fleft(gleft(8right)right)[/latex]
- [latex]fleft(gleft(5right)right)[/latex]
Show Solution
9
- [latex]gleft(fleft(5right)right)[/latex]
- [latex]gleft(fleft(3right)right)[/latex]
Show Solution
4
- [latex]fleft(fleft(4right)right)[/latex]
- [latex]fleft(fleft(1right)right)[/latex]
Show Solution
2
- [latex]gleft(gleft(2right)right)[/latex]
- [latex]gleft(gleft(6right)right)[/latex]
Show Solution
3
For the following exercises, use the function values for [latex],ftext{ and }g,[/latex] shown in Table 4 to evaluate the expressions.
| [latex]x[/latex] | [latex]fleft(xright)[/latex] | [latex]gleft(xright)[/latex] |
| [latex]-3[/latex] | 11 | [latex]-8[/latex] |
| [latex]-2[/latex] | 9 | [latex]-3[/latex] |
| [latex]-1[/latex] | 7 | 0 |
| 0 | 5 | 1 |
| 1 | 3 | 0 |
| 2 | 1 | [latex]-3[/latex] |
| 3 | [latex]-1[/latex] | [latex]-8[/latex] |
- [latex]left(fcirc gright)left(1right)[/latex]
- [latex]left(fcirc gright)left(2right)[/latex]
Show Solution
11
- [latex]left(gcirc fright)left(2right)[/latex]
- [latex]left(gcirc fright)left(3right)[/latex]
Show Solution
0
- [latex]left(gcirc gright)left(1right)[/latex]
- [latex]left(fcirc fright)left(3right)[/latex]
Show Solution
7
For the following exercises, use each pair of functions to find[latex],fleft(gleft(0right)right),[/latex]and[latex],gleft(fleft(0right)right).[/latex]
- [latex]fleft(xright)=4x+8,,gleft(xright)=7-{x}^{2}[/latex]
- [latex]fleft(xright)=5x+7,,gleft(xright)=4-2{x}^{2}[/latex]
Show Solution
[latex]fleft(gleft(0right)right)=27,,gleft(fleft(0right)right)=-94[/latex]
- [latex]fleft(xright)=sqrt{x+4},,gleft(xright)=12-{x}^{3}[/latex]
- [latex]fleft(xright)=frac{1}{x+2},,gleft(xright)=4x+3[/latex]
Show Solution
[latex]fleft(gleft(0right)right)=frac{1}{5},,gleft(fleft(0right)right)=5[/latex]
For the following exercises, use the functions[latex],fleft(xright)=2{x}^{2}+1,[/latex]and[latex],gleft(xright)=3x+5,[/latex]
to evaluate or find the composite function as indicated.
- [latex]fleft(gleft(2right)right)[/latex]
- [latex]fleft(gleft(xright)right)[/latex]
Show Solution
[latex]18{x}^{2}+60x+51[/latex]
- [latex]gleft(fleft(-3right)right)[/latex]
- [latex]left(gcirc gright)left(xright)[/latex]
Show Solution
[latex]gcirc gleft(xright)=9x+20[/latex]
Extensions
For the following exercises, use[latex],fleft(xright)={x}^{3}+1,[/latex]and[latex],gleft(xright)=sqrt[3]{x-1}.[/latex]
- Find[latex],left(fcirc gright)left(xright),[/latex]and[latex],left(gcirc fright)left(xright).[/latex]Compare the two answers.
- Find[latex],left(fcirc gright)left(2right),[/latex]and[latex],left(gcirc fright)left(2right).[/latex]
Show Solution
2
- What is the domain of[latex],left(gcirc fright)left(xright)?[/latex]
- What is the domain of[latex],left(fcirc gright)left(xright)?[/latex]
Show Solution
[latex]left(-infty ,infty right)[/latex]
- Let[latex],fleft(xright)=frac{1}{x}.[/latex]
- Find[latex],left(fcirc fright)left(xright).[/latex]
- Is[latex],left(fcirc fright)left(xright),[/latex]for any function[latex],f,[/latex]the same result as the answer to part (a) for any function? Explain.
For the following exercises, let[latex],Fleft(xright)={left(x+1right)}^{5},,[/latex][latex]fleft(xright)={x}^{5},,[/latex]and[latex],gleft(xright)=x+1.[/latex]
- True or False:[latex],left(gcirc fright)left(xright)=Fleft(xright).[/latex]
Show Solution
False
- True or False:[latex],left(fcirc gright)left(xright)=Fleft(xright).[/latex]
For the following exercises, find the composition when[latex],fleft(xright)={x}^{2}+2,[/latex]for all[latex],xge 0,[/latex]and[latex],gleft(xright)=sqrt{x-2}.[/latex]
- [latex]left(fcirc gright)left(6right);,left(gcirc fright)left(6right)[/latex]
Show Solution
[latex]left(fcirc gright)left(6right)=6[/latex]; [latex],left(gcirc fright)left(6right)=6[/latex]
- [latex]left(gcirc fright)left(aright);,left(fcirc gright)left(aright)[/latex]
- [latex]left(fcirc gright)left(11right);,left(gcirc fright)left(11right)[/latex]
Show Solution
[latex]left(fcirc gright)left(11right)=11,,,left(gcirc fright)left(11right)=11[/latex]
Real-World Applications
- The function[latex],Dleft(pright),[/latex]gives the number of items that will be demanded when the price is[latex],p.[/latex]The production cost[latex],Cleft(xright),[/latex]is the cost of producing[latex],x,[/latex]items. To determine the cost of production when the price is $6, you would do which of the following?
- Evaluate[latex],Dleft(Cleft(6right)right).[/latex]
- Evaluate[latex],Cleft(Dleft(6right)right).[/latex]
- Solve[latex],Dleft(Cleft(xright)right)=6.[/latex]
- Solve[latex],Cleft(Dleft(pright)right)=6.[/latex]
- The function[latex],Aleft(dright),[/latex]gives the pain level on a scale of 0 to 10 experienced by a patient with[latex],d,[/latex]milligrams of a pain-reducing drug in her system. The milligrams of the drug in the patient’s system after[latex],t,[/latex]minutes is modeled by[latex],mleft(tright).[/latex]Which of the following would you do in order to determine when the patient will be at a pain level of 4?
- Evaluate[latex],Aleft(mleft(4right)right).[/latex]
- Evaluate[latex],mleft(Aleft(4right)right).[/latex]
- Solve[latex],Aleft(mleft(tright)right)=4.[/latex]
- Solve[latex],mleft(Aleft(dright)right)=4.[/latex]
Show Solution
c
- A store offers customers a 30% discount on the price[latex],x,[/latex]of selected items. Then, the store takes off an additional 15% at the cash register. Write a price function[latex],Pleft(xright),[/latex]that computes the final price of the item in terms of the original price[latex],x.[/latex](Hint: Use function composition to find your answer.)
- A rain drop hitting a lake makes a circular ripple. If the radius, in inches, grows as a function of time in minutes according to[latex],rleft(tright)=25sqrt{t+2},,[/latex]find the area of the ripple as a function of time. Find the area of the ripple at[latex],t=2.[/latex]
Show Solution
[latex]Aleft(tright)=pi {left(25sqrt{t+2}right)}^{2},[/latex]and[latex],Aleft(2right)=pi {left(25sqrt{4}right)}^{2}=2500pi[/latex] square inches
- A forest fire leaves behind an area of grass burned in an expanding circular pattern. If the radius of the circle of burning grass is increasing with time according to the formula[latex],rleft(tright)=2t+1,,[/latex]express the area burned as a function of time,[latex],t,[/latex](minutes).
- Use the function you found in the previous exercise to find the total area burned after 5 minutes.
Show Solution
[latex]Aleft(5right)=pi {left(2left(5right)+1right)}^{2}=121pi ,[/latex]square units
- The radius[latex],r,,[/latex]in inches, of a spherical balloon is related to the volume,[latex],V,,[/latex]by[latex],rleft(Vright)=sqrt[3]{frac{3V}{4pi }}.[/latex]Air is pumped into the balloon, so the volume after[latex],t,[/latex]seconds is given by[latex],Vleft(tright)=10+20t.[/latex]
- Find the composite function[latex],rleft(Vleft(tright)right).[/latex]
- Find the exact time when the radius reaches 10 inches.
- The number of bacteria in a refrigerated food product is given by [latex]Nleft(Tright)=23{T}^{2}-56T+1,,[/latex][latex]3
33,,[/latex]where[latex],T[/latex] is the temperature of the food. When the food is removed from the refrigerator, the temperature is given by [latex]Tleft(tright)=5t+1.5,[/latex] where [latex]t[/latex] is the time in hours.
- Find the composite function[latex],Nleft(Tleft(tright)right).[/latex]
- Find the time (round to two decimal places) when the bacteria count reaches 6752.
Show Solution
a.[latex],Nleft(Tleft(tright)right)=23{left(5t+1.5right)}^{2}-56left(5t+1.5right)+1;,[/latex]
b. 3.38 hours
Glossary
- binomial
- a polynomial containing two terms
- coefficient
- any real number[latex],{a}_{i},[/latex]in a polynomial in the form[latex],{a}_{n}{x}^{n}+...+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0}[/latex]
- degree
- the highest power of the variable that occurs in a polynomial
- difference of squares
- the binomial that results when a binomial is multiplied by a binomial with the same terms, but the opposite sign
- leading coefficient
- the coefficient of the leading term
- leading term
- the term containing the highest degree
- monomial
- a polynomial containing one term
- perfect square trinomial
- the trinomial that results when a binomial is squared
- polynomial
- a sum of terms each consisting of a variable raised to a nonnegative integer power
- term of a polynomial
- any[latex],{a}_{i}{x}^{i},[/latex]of a polynomial in the form[latex],{a}_{n}{x}^{n}+...+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0}[/latex]
- trinomial
- a polynomial containing three terms
- composite function
- the new function formed by function composition, when the output of one function is used as the input of another
Media Attributions
- 1.4 Polynomial Graphic © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 1.4 FOIL Graphic © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 1.4 Using FOIL I © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 1.4 Using FOIL II © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 1.4 Using FOIL III © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 1.4 Using FOIL IV © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 3.5 Explanation of Composite Function © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
- 3.5 Figure 1 © OpenStax Algebra and Trigonometry, 2e is licensed under a CC BY (Attribution) license
- 3.5 Figure 2 © OpenStax Algebra and Trigonometry, 2e is licensed under a CC BY (Attribution) license
- 3.5 Figure 3 © OpenStax Algebra and Trigonometry, 2e is licensed under a CC BY (Attribution) license
- 3.5 Figure 4 © OpenStax Algebra and Trigonometry
- 3.5 Figure 5 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 3.5 Figure 6 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 3.5 Figure 7 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 3.5 Figure 8 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license

