"

0.1 Divisibility and Factorization

Karen Perilloux; Prakash Ghimire; and Lauren Johnson

Learning Objectives

By the end of this section, you will be able to:

  • Find the prime factorization of a composite number
  • Find the least common multiple (LCM) of two numbers

Find the Prime Factorization of a Composite Number

In the previous section, we found the factors of a number. Prime numbers have only two factors, the number 1 and the prime number itself. Composite numbers have more than two factors, and every composite number can be written as a unique product of primes. This is called the prime factorization of a number. When we write the prime factorization of a number, we are rewriting the number as a product of primes. Finding the prime factorization of a composite number will help you later in this course.

Prime Factorization

The prime factorization of a number is the product of prime numbers that equals the number.

You may want to refer to the following list of prime numbers less than 50 as you work through this section: $$ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47 $$

Prime Factorization Using the Factor Tree Method

One way to find the prime factorization of a number is to make a factor tree. We start by writing the number, and then writing it as the product of two factors. We write the factors below the number and connect them to the number with a small line segment—a “branch” of the factor tree.

If a factor is prime, we circle it (like a bud on a tree), and do not factor that “branch” any further. If a factor is not prime, we repeat this process, writing it as the product of two factors and adding new branches to the tree.

We continue until all the branches end with a prime. When the factor tree is complete, the circled primes give us the prime factorization.

For example, let’s find the prime factorization of 36. We can start with any factor pair such as 3 and 12. We write 3 and 12 below 36 with branches connecting them.

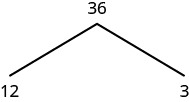
The figure shows a factor tree with the number 36 at the top. Two branches are splitting out from under 36. The right branch has a number 3 at the end with a circle around it. The left branch has the number 12 at the end.
The factor 3 is prime, so we circle it. The factor 12 is composite, so we need to find its factors. Let’s use 3 and 4. We write these factors on the tree under the 12.

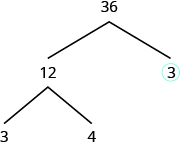
The figure shows a factor tree with the number 36 at the top. Two branches are splitting out from under 36. The right branch has a number 3 at the end with a circle around it. The left branch has the number 12 at the end. Two more branches are splitting out from under 12. The right branch has the number 4 at the end and the left branch has the number 3 at the end.
The factor 3 is prime, so we circle it. The factor 4 is composite, and it factors into 2 · 2. We write these factors under the 4. Since 2 is prime, we circle both 2s.

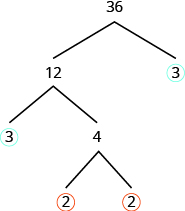
The figure shows a factor tree with the number 36 at the top. Two branches are splitting out from under 36. The right branch has a number 3 at the end with a circle around it. The left branch has the number 12 at the end. Two more branches are splitting out from under 12. The right branch has the number 4 at the end and the left branch has the number 3 at the end with a circle around it. Two more branches are splitting out from under 4. Both the left and right branch have the number 2 at the end with a circle around it.
The prime factorization is the product of the circled primes. We generally write the prime factorization in order from least to greatest.

$$ 2 \cdot 2 \cdot 3 \cdot 3 $$
In cases like this, where some of the prime factors are repeated, we can write prime factorization in exponential form.
$$ 2 \cdot 2 \cdot 3 \cdot 3 $$
$$ 2^2 \cdot 3^2 $$
Note that we could have started our factor tree with any factor pair of 36. We chose 12 and 3, but the same result would have been the same if we had started with 2 and 18, 4 and 9, or 6 and 6.

How To

Find the prime factorization of a composite number using the tree method.

  1. Find any factor pair of the given number, and use these numbers to create two branches.
  2. If a factor is prime, that branch is complete. Circle the prime.
  3. If a factor is not prime, write it as the product of a factor pair and continue the process.
  4. Write the composite number as the product of all the circled primes.

Mathispower4u. Ex 1: Prime Factorization. YouTube. https://www.youtube.com/watch?v=V_wBWdndCuw

 

Example

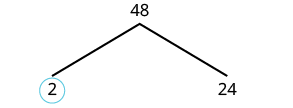
Find the prime factorization of 48 using the factor tree method.

Show Solution
We can start our tree using any factor pair of 48. Let’s use 2 and 24.

We circle the 2 because it is prime and so that branch is complete.

 Factor tree of 48 showing 1 level of factors: 2 and 24.
Now we will factor 24. Let’s use 4 and 6. 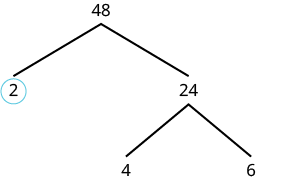Factor tree of 48 showing first level of factors: 2 and 24. Second level of factors of 24 is 4 and 6.

Neither factor is prime, so we do not circle either.
We factor the 4, using 2 and 2.
We factor 6, using 2 and 3.We circle the 2s and the 3 since they are prime. Now all of the branches end in a prime.

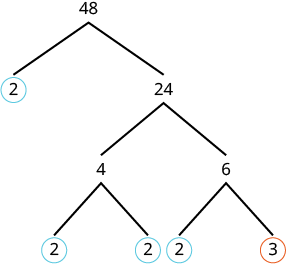 Factor tree of 48 showing first level of factors: 2 and 24. Second level of factors of 24 is 4 and 6. Third level of factors of 4 is 2 and 2, next level of factors of 6 is 2 and 3.
Write the product of the circled numbers. [latex]2 \cdot 2 \cdot 2 \cdot 2 \cdot 3[/latex]
Write in exponential form. [latex]2^4 \cdot 3[/latex]

Try It

Find the prime factorization using the factor tree method: [latex]80[/latex]

Show Solution

[latex]2^4 \times 5[/latex]

 

Try It

Find the prime factorization using the factor tree method: [latex]60[/latex]

Show Solution

[latex]2^2 \times 3 \times 5[/latex]

 

Example

Find the prime factorization of [latex]84[/latex] using the factor tree method.

Show Solution

 

Draw a factor tree of 84.

We start with the factor pair 4 and 21. Neither factor is prime so we factor them further. 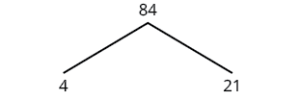Factor tree of 48 showing 1 level of factors: 4 and 21.
Now the factors are all prime, so we circle them. 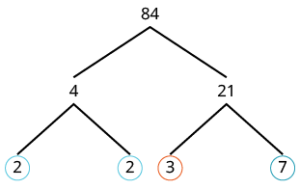Factor tree of 84 showing first level of factors: 4 and 21. Second level of factors of 4 is 2 and 2 with circle on each 2. Second level factors of 21 is 3 and 7 with circle on 3 and 7.
Then we write 84 as the product of all circled primes.

Try It

Find the prime factorization using the factor tree method: [latex]126[/latex]

Show Solution

[latex]2 \times 3^2 \times 7[/latex]

 

Try It

Find the prime factorization using the factor tree method: [latex]294[/latex]

Show Solution

[latex]2 \times 3 \times 7^2[/latex]

 

Prime Factorization Using the Ladder Method

The ladder method is another way to find the prime factors of a composite number. It leads to the same result as the factor tree method. Some people prefer the ladder method to the factor tree method, and vice versa. To begin building the “ladder,” divide the given number by its smallest prime factor. For example, to start the ladder for 36, we divide 36 by 2, the smallest prime factor of 36.
The image shows the division of 2 into 36 to get the quotient 18. This division is represented using a division bracket with 2 on the outside left of the bracket, 36 inside the bracket and 18 above the 36, outside the bracket.
To add a “step” to the ladder, we continue dividing by the same prime until it no longer divides evenly.
The image shows the division of 2 into 36 to get the quotient 18. This division is represented using a division bracket with 2 on the outside left of the bracket, 36 inside the bracket and 18 above the 36, outside the bracket. Another division bracket is written around the 18 with a 2 on the outside left of the bracket and a 9 above the 18, outside of the bracket.
Then we divide by the next prime; so we divide 9 by 3.
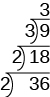
The image shows the division of 2 into 36 to get the quotient 18. This division is represented using a division bracket with 2 on the outside left of the bracket, 36 inside the bracket and 18 above the 36, outside the bracket. Another division bracket is written around the 18 with a 2 on the outside left of the bracket and a 9 above the 18, outside of the bracket. Another division bracket is written around the 9 with a 3 on the outside left of the bracket and a 3 above the 9, outside of the bracket.
We continue dividing up the ladder in this way until the quotient is prime. Since the quotient, 3, is prime, we stop here. Do you see why the ladder method is sometimes called stacked division? The prime factorization is the product of all the primes on the sides and top of the ladder.
2⋅2⋅3⋅322⋅322⋅2⋅3⋅322⋅32

Notice that the result is the same as we obtained with the factor tree method.

How To

Find the prime factorization of a composite number using the ladder method.

  1. Divide the number by the smallest prime.
  2. Continue dividing by that prime until it no longer divides evenly.
  3. Divide by the next prime until it no longer divides evenly.
  4. Continue until the quotient is a prime.
  5. Write the composite number as the product of all the primes on the sides and top of the ladder.

Example

Find the prime factorization of [latex]120[/latex] using the ladder method.

 

Show Solution
Divide the number by the smallest prime, which is 2. The image shows the division of 2 into 120 to get the quotient 60. This division is represented using a division bracket with 2 on the outside left of the bracket, 120 inside the bracket and 60 above the 120, outside the bracket.
Continue dividing by 2 until it no longer divides evenly. 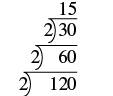The image shows the division of 2 into 120 to get the quotient 60. This division is represented using a division bracket with 2 on the outside left of the bracket, 120 inside the bracket and 60 above the 120, outside the bracket. Another division bracket is written around the 60 with a 2 on the outside left of the bracket and a 30 above the 60, outside of the bracket. Another division bracket is written around the 30 with a 2 on the outside left of the bracket and a 15 above the 30, outside of the bracket.
Divide by the next prime, 3. 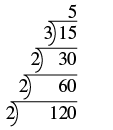The image shows the division of 2 into 120 to get the quotient 60. This division is represented using a division bracket with 2 on the outside left of the bracket, 120 inside the bracket and 60 above the 120, outside the bracket. Another division bracket is written around the 60 with a 2 on the outside left of the bracket and a 30 above the 60, outside of the bracket. Another division bracket is written around the 30 with a 2 on the outside left of the bracket and a 15 above the 30, outside of the bracket. Another division bracket is written around the 15 with a 3 on the outside left of the bracket and a 5 above the 15, outside of the bracket.
The quotient, 5, is prime, so the ladder is complete. Write the prime factorization of 120. 2⋅2⋅2⋅3⋅52⋅2⋅2⋅3⋅5 23⋅3⋅5

Check this yourself by multiplying the factors. The result should be 120 .

 

Try It

Find the prime factorization using the ladder method: [latex]80[/latex]

Show Solution

[latex]2^4 \times 5[/latex]

 

Try It

Find the prime factorization using the ladder method: [latex]60[/latex]

Show Solution

[latex]2^2 \times 3 \times 5[/latex]

 

Example

Find the prime factorization of [latex]48[/latex] using the ladder method.

Show Solution
Divide the number by the smallest prime, 2. The image shows the division of 2 into 48 to get the quotient 24. This division is represented using a division bracket with 2 on the outside left of the bracket, 48 inside the bracket and 24 above the 48, outside the bracket.
Continue dividing by 2 until it no longer divides evenly. 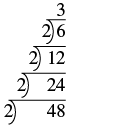The image shows the division of 2 into 24 to get the quotient 48. This division is represented using a division bracket with 2 on the outside left of the bracket, 48 inside the bracket and 24 above the 48, outside the bracket. Another division bracket is written around the 24 with a 2 on the outside left of the bracket and a 12 above the 24, outside of the bracket. Another division bracket is written around the 12 with a 2 on the outside left of the bracket and a 6 above the 12, outside of the bracket. Another division bracket is written around the 6 with a 2 on the outside left of the bracket and a 3 above the 6, outside of the bracket.
The quotient, 3, is prime, so the ladder is complete. Write the prime factorization of 48. 2⋅2⋅2⋅2⋅32⋅2⋅2⋅2⋅3 24⋅324⋅3

 

Try It

Find the prime factorization using the ladder method. [latex]126[/latex]

Show Solution

[latex]2 \times 3^2 \times 7[/latex]

 

Try It

Find the prime factorization using the ladder method. [latex]294[/latex]

Show Solution

[latex]2 \times 3 \times 7^2[/latex]

 

Find the Least Common Multiple (LCM) of Two Numbers

One of the reasons we look at multiples and primes is to use these techniques to find the least common multiple of two numbers. This will be useful when we add and subtract fractions with different denominators.

Listing Multiples Method

A common multiple of two numbers is a number that is a multiple of both numbers. Suppose we want to find common multiples of 10 and 25. We can list the first several multiples of each number. Then we look for multiples that are common to both lists—these are the common multiples.

10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, …

25: 25, 50, 75, 100, 125, …

We see that 50 and 100 appear in both lists. They are common multiples of 10 and 25. We would find more common multiples if we continued the list of multiples for each.
The smallest number that is a multiple of two numbers is called the least common multiple(LCM). So the least LCM of 10 and 25 is 50.

How To

Find the least common multiple (LCM) of two numbers by listing multiples.

  1. List the first several multiples of each number.
  2. Look for multiples common to both lists. If there are no common multiples in the lists, write out additional multiples for each number.
  3. Look for the smallest number that is common to both lists.
  4. This number is the LCM.

Example

Find the LCM of 15 and 20 by listing multiples.

Show Solution

List the first several multiples of 15 and of 20. Identify the first common multiple.

15: 15, 30, 45, [latex]60[/latex], 75, 90, 105, 120

20: 20, 40, [latex]60[/latex], 80, 100, 120, 140. 160

The smallest number to appear on both lists is 60, so 60 is the least common multiple of 15 and 20.

Notice that 120 is on both lists, too. It is a common multiple, but it is not the least common multiple.

Try It

Find the least common multiple (LCM) of the given numbers: 9 and 12

Show Solution

[latex]36[/latex]

Try It

Find the least common multiple (LCM) of the given numbers: 18 and 24

Show Solution

[latex]72[/latex]

Prime Factors Method

Another way to find the least common multiple of two numbers is to use their prime factors. We’ll use this method to find the LCM of 12 and 18.

We start by finding the prime factorization of each number.

12=2⋅2⋅318=2⋅3⋅312=2⋅2⋅318=2⋅3⋅3

Then we write each number as a product of primes, matching primes vertically when possible.

12=2⋅2⋅318=2⋅3⋅312=2⋅2⋅318=2⋅3⋅3

Now we bring down the primes in each column. The LCM is the product of these factors.


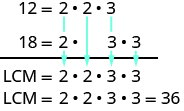
The image shows the prime factorization of 12 written as the equation 12 equals 2 times 2 times 3. Below this equation is another showing the prime factorization of 18 written as the equation 18 equals 2 times 3 times 3. The two equations line up vertically at the equal symbol. The first 2 in the prime factorization of 12 aligns with the 2 in the prime factorization of 18. Under the second 2 in the prime factorization of 12 is a gap in the prime factorization of 18. Under the 3 in the prime factorization of 12 is the first 3 in the prime factorization of 18. The second 3 in the prime factorization has no factors above it from the prime factorization of 12. A horizontal line is drawn under the prime factorization of 18. Below this line is the equation LCM equal to 2 times 2 times 3 times 3. Arrows are drawn down vertically from the prime factorization of 12 through the prime factorization of 18 ending at the LCM equation. The first arrow starts at the first 2 in the prime factorization of 12 and continues down through the 2 in the prime factorization of 18. Ending with the first 2 in the LCM. The second arrow starts at the next 2 in the prime factorization of 12 and continues down through the gap in the prime factorization of 18. Ending with the second 2 in the LCM. The third arrow starts at the 3 in the prime factorization of 12 and continues down through the first 3 in the prime factorization of 18. Ending with the first 3 in the LCM. The last arrow starts at the second 3 in the prime factorization of 18 and points down to the second 3 in the LCM.

Notice that the prime factors of 12 and the prime factors of 18 are included in the LCM. By matching up the common primes, each common prime factor is used only once. This ensures that 36 is the least common multiple.

How To

Find the LCM using the prime factors method.

  1. Find the prime factorization of each number.
  2. Write each number as a product of primes, matching primes vertically when possible.
  3. Bring down the primes in each column.
  4. Multiply the factors to get the LCM.

Example

Find the LCM of 15 and 18 using the prime factors method.

Show Solution

 

Write each number as a product of primes. The image shows the prime factorization of 15 written as the equation 15 equals 3 times 5 on the left and the prime factorization of 18 written as the equation 18 equals 2 times 3 times 3 on the right.
Write each number as a product of primes, matching primes vertically when possible. The image shows the prime factorization of 15 written as the equation 15 equals 3 times 5 on the top and the prime factorization of 18 written as the equation 18 equals 2 times 3 times 3 below.
Bring down the primes in each column. 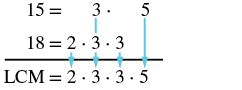The image shows the prime factorization of 15 written as the equation 15 equals 3 times 5 on the top row and the prime factorization of 18 written as the equation 18 equals 2 times 3 times 3 on the second row and a stright line below it. The last row is the LCM of 15 and 18 written as the equation LCM equals 2 times 3 times 3 times 5
Multiply the factors to get the LCM. LCM=2⋅3⋅3⋅5LCM=2⋅3⋅3⋅5

The LCM of 15 and 18 is 90.

 

Try It

Find the LCM using the prime factors method:  15 and 20

Show Solution

[latex]60[/latex]

 

Try It

Find the LCM using the prime factors method: 15 and 35

Show Solution

[latex]105[/latex]

 

Example

Find the LCM of 50 and 100 using the prime factors method.

 

Show Solution
Write the prime factorization of each number. The image shows the prime factorization of 50 written as the equation 50 equals 2 times 5 times 5 on the left and the prime factorization of 100 written as the equation 100 equals 2 times 2 times 5 times 5 on the right.
Write each number as a product of primes, matching primes vertically when possible. The image shows the prime factorization of 50 written as the equation 50 equals 2 times 5 times 5 on the top and the prime factorization of 100 written as the equation 100 equals 2 times 2 times 5 times 5 below.
Bring down the primes in each column. 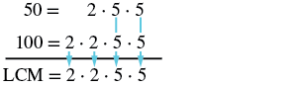The image shows the prime factorization of 50 written as the equation 50 equals 2 times 5 times 5 on the top row and the prime factorization of 100 written as the equation 100 equals 2 times 2 times 5 times 5 on the second row and a stright line below it. The last row is the LCM of 50 and 100 written as the equation LCM equals 2 times 2 times 5 times 5
Multiply the factors to get the LCM. LCM=2⋅2⋅5⋅5LCM=2⋅2⋅5⋅5

The LCM of 50 and 100 is 100.

Try It

Find the LCM  of [latex]55[/latex] and [latex]88[/latex] using the prime factors method.

Show Solution

[latex]1320[/latex]

 

Try It

Find the LCM of [latex]60[/latex] and [latex]72[/latex] using the prime factors method.

Show Solution

[latex]360[/latex]

 

Key Concepts

Find the prime factorization of a composite number using the tree method.

  • Step 1.  Find any factor pair of the given number, and use these numbers to create two branches.
  • Step 2.  If a factor is prime, that branch is complete. Circle the prime.
  • Step 3.  If a factor is not prime, write it as the product of a factor pair and continue the process.
  • Step 4.  Write the composite number as the product of all the circled primes.

Find the prime factorization of a composite number using the ladder method.

  • Step 1.  Divide the number by the smallest prime.
  • Step 2.  Continue dividing by that prime until it no longer divides evenly.
  • Step 3.  Divide by the next prime until it no longer divides evenly.
  • Step 4.  Continue until the quotient is a prime.
  • Step 5.  Write the composite number as the product of all the primes on the sides and top of the ladder.

Find the LCM by listing multiples.

  • Step 1.  List the first several multiples of each number.
  • Step 2.  Look for multiples common to both lists. If there are no common multiples in the lists, write out additional multiples for each number.
  • Step 3.  Look for the smallest number that is common to both lists.
  • Step 4.  This number is the LCM.

Find the LCM using the prime factors method.

  • Step 1.  Find the prime factorization of each number.
  • Step 2.  Write each number as a product of primes, matching primes vertically when possible.
  • Step 3.  Bring down the primes in each column.
  • Step 4.  Multiply the factors to get the LCM.

 

Section Exercises

Find the Prime Factorization of a Composite Number

In the following exercises, find the prime factorization of each number using the factor tree method.

1. 86

Show Solution

2 ⋅ 43

 

2. 78

3. 132

Show Solution

2 ⋅ 2 ⋅ 3 ⋅ 11

 

4. 455

5. 693

Show Solution

3 ⋅ 3 ⋅ 7 ⋅ 11

 

6. 420

7. 115

Show Solution

5 ⋅ 23

 

8. 225

9. 2475

Show Solution

3 ⋅ 3 ⋅ 5 ⋅ 5 ⋅ 11

 

10. 1560

In the following exercises, find the prime factorization of each number using the ladder method.

11. 56

Show Solution

2 ⋅ 2 ⋅ 2 ⋅ 7

 

12. 72

13. 168

Show Solution

2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 7

 

14. 252

15. 391

Show Solution

17 ⋅ 23

 

16. 400

17. 432

Show Solution

2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3

 

18. 627

19. 2160

Show Solution

2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 5

 

20. 2520

In the following exercises, find the prime factorization of each number using any method.

21. 150

Show Solution

2 ⋅ 3 ⋅ 5 ⋅ 5

 

22. 180

23. 525

Show Solution

3 ⋅ 5 ⋅ 5 ⋅ 7

 

24.. 444

25. 36

Show Solution

3 ⋅ 5 ⋅ 5 ⋅ 7

 

26. 50

27. 350

Show Solution

2 ⋅ 5 ⋅ 5 ⋅ 7

 

28. 144

 

Find the Least Common Multiple (LCM) of Two Numbers

In the following exercises, find the least common multiple (LCM) by listing multiples.

29. 8 and 12

Show Solution

24

 

30. 4 and 3

31. 6 and 15

Show Solution

30

 

32. 12 and 16

33. 30 and 40

Show Solution

120

 

34. 20 and 30

35. 60 and 70

Show Solution

300

 

36. 44 and 55

44,55

In the following exercises, find the least common multiple (LCM) by using the prime factors method.

37. 8 and 12

Show Solution

24

 

38. 12 and 16

39. 24 and 30

Show Solution

120

 

40. 28 and 40

41. 70 and 84

Show Solution

420

 

42. 84 and 90

 

In the following exercises, find the least common multiple (LCM) using any method.

43. 6 and 21

Show Solution

42

 

44. 9 and 15

45. 24 and 30

Show Solution

120

 

46. 32 and 40

Everyday Math

47. Grocery shopping Hot dogs are sold in packages of ten, but hot dog buns come in packs of eight. What is the smallest number of hot dogs and buns that can be purchased if you want to have the same number of hot dogs and buns? (Hint: it is the LCM!)

Show Solution

40

 

48.  Grocery shopping Paper plates are sold in packages of 12 and party cups come in packs of 8. What is the smallest number of plates and cups you can purchase if you want to have the same number of each? (Hint: it is the LCM!)

Writing Exercises

49.  Do you prefer to find the prime factorization of a composite number by using the factor tree method or the ladder method? Why?

50.  Do you prefer to find the LCM by listing multiples or by using the prime factors method? Why?

 

Glossary

composite number

A composite number is a counting number that is not prime.

least common multiple

The smallest number that is a multiple of two numbers is called the least common multiple (LCM).

multiple of a number

A number is a multiple of n if it is the product of a counting number and n.

prime number

A prime number is a counting number greater than 1 whose only factors are 1 and itself.

prime factorization

The prime factorization of a number is the product of prime numbers that equals the number.

 

Media Attributions

License

Icon for the Creative Commons Attribution 4.0 International License

0.1 Divisibility and Factorization Copyright © by Karen Perilloux; Prakash Ghimire; and Lauren Johnson is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book