0.3 Unit Conversions

Karen Perilloux; Prakash Ghimire; Kristina VanDusen; Lauren Johnson

0.3 Unit Conversions

Karen Perilloux; Prakash Ghimire; Kristina VanDusen; and Lauren Johnson

Learning Objectives

By the end of this section, you will be able to:

Make unit conversions in the U.S. system
Use mixed units of measurement in the U.S. system
Make unit conversions in the metric system
Use mixed units of measurement in the metric system
Convert between the U.S. and the metric systems of measurement
Convert between Fahrenheit and Celsius temperatures
Understand the role of units in measurement
Find conversion factors relating two units
Convert between units
Carry out rate conversions for computations involving two or more properties

In this section, we will see how to convert different types of units, such as feet to miles or kilograms to pounds. The basic idea in all of the unit conversions will be to use a form of 1, the multiplicative identity, to change the units but not the value of a quantity.

Make Unit Conversions in the U.S. System

There are two systems of measurement commonly used around the world. Most countries use the metric system. The United States uses a different system of measurement, usually called the U.S. system. We will look at the U.S. system first.

The U.S. system of measurement uses units of inch, foot, yard, and mile to measure length and pound and ton to measure weight. For capacity, the units used are cup, pint, quart, and gallon. Both the U.S. system and the metric system measure time in seconds, minutes, or hours.

The equivalencies among the basic units of the U.S. system of measurement are listed in the table below. The table also shows, in parentheses, the common abbreviations for each measurement.

U.S. System Units

Length

Volume

1

foot (ft) =

12

inches (in)

1

yard (yd) =

3

feet (ft)

1

mile (mi) =

5280

feet (ft)

3

teaspoons (t) =

1

tablespoon (T)

16

Tablespoons (T) =

1

cup (C)

1

cup (C) =

8

fluid ounces (fl oz)

1

pint (pt) =

2

cups (C)

1

quart (qt) =

2

pints (pt)

1

gallon (gal) =

4

quarts (qt)

Weight

Time

1

pound (lb) =

16

ounces (oz)

1

ton =

2000

pounds (lb)

1

minute (min) =

60

seconds (s)

1

hour (h) =

60

minutes (min)

1

day =

24

hours (h)

1

week (wk) =

7

days

1

year (yr) =

365

days

In many real-life applications, we need to convert between units of measurement. We will use the identity property of multiplication to do these conversions. We’ll restate the Identity Property of Multiplication here for easy reference.

For any real number [latex]a[/latex], [latex]a \cdot 1 = a[/latex] [latex]1 \cdot a = a[/latex]

To use the identity property of multiplication, we write [latex]1[/latex] in a form that will help us convert the units. For example, suppose we want to convert inches to feet. We know that [latex]1[/latex] foot is equal to [latex]12[/latex] inches, so we can write [latex]1[/latex] as the fraction [latex]\frac{1 ft}{12 in}[/latex]. When we multiply by this fraction, we do not change the value but just change the units. But [latex]\frac{12 in}{1 ft}[/latex] also equals [latex]1[/latex]. How do we decide whether to multiply by [latex]\frac{1 ft}{12 in}[/latex] or [latex]\frac{12 in}{1 ft}[/latex] ? We choose the fraction that will make the units we want to convert from divide out. For example, suppose we wanted to convert [latex]60[/latex] inches to feet. If we choose the fraction that has inches in the denominator, we can eliminate the inches.

\[
60 \,\text{in} \cdot \frac{1 \,\text{ft}}{12 \,\text{in}} = 5 \,\text{ft}
\]

On the other hand, if we wanted to convert [latex]5[/latex] feet to inches, we would choose the fraction that has feet in the denominator.

\[
5 \,\text{ft} \cdot \frac{12 \,\text{in}}{1 \,\text{ft}} = 60 \,\text{in}
\]

We treat the unit words like factors and ‘divide out’ common units like we do common factors.

How To

Make unit conversions.

Step 1. Multiply the measurement to be converted by [latex]1[/latex]; write [latex]1[/latex] as a fraction relating the units given and the units needed.

Step 2. Multiply.

Step 3. Simplify the fraction, performing the indicated operations and removing the common units

Example

Mary Anne is [latex]66[/latex] inches tall. What is her height in feet?

Show Solution

We will convert grams to kilograms.

Convert 66 inches into feet.

Multiply the measurement to be converted by 1.

[latex]66 \text{inches} \cdot 1[/latex]

Write 1 as a fraction relating the units given and the units needed.

[latex]66 \text{inches} \cdot \frac{1 \text{foot}}{12 \text{inches}}[/latex]

Multiply.

[latex]\frac{66 \ \text{inches} \cdot 1 \text{foot}}{12 \text{inches}}[/latex]

Simplify the fraction.

\[
\frac{66 \,\cancel{\text{ inches}} \cdot 1 \text{ ft}}{12 \,\cancel{\text{ inches}}}
\]

[latex]\frac{66 \ \text{feet}}{12}[/latex]

[latex]5.5 \text{feet}[/latex]

Notice that the when we simplified the fraction, we first divided out the inches. Mary Anne is [latex]5.5[/latex] feet tall.

Try It

Lexie is [latex]30[/latex] inches tall. Convert her height to feet.

Show Solution

[latex]2.5[/latex] feet

Try It

Rene bought a hose that is [latex]18[/latex] yards long. Convert the length to feet.

Show Solution

[latex]54[/latex] feet

When we use the Identity Property of Multiplication to convert units, we need to make sure the units we want to change from will divide out. Usually this means we want the conversion fraction to have those units in the denominator.

Example

Ndula, an elephant at the San Diego Safari Park, weighs almost [latex]3.2[/latex] tons. Convert her weight to pounds.

A photograph of an adult elephant. — Figure 1 ( Credit: Guldo Da Rozze, Flickr)

Show Solution

We will convert [latex]3.2[/latex] tons into pounds. We will use the Identity Property of multiplication, writing [latex]1[/latex] as the fraction [latex]\frac{2000 \text{ lbs} }{1 \text{ ton}}[/latex].

3.2 tons

Multiply the measurement to be converted by 1.

3.2 tons \cdot 1

Write 1 as a fraction relating tons and pounds.

3.2 tons \cdot \frac{2000 lbs}{1 ton}

Simplify.

\frac{3.2 tons \cdot 2000 lbs}{1 ton}

Multiply.

6400 lbs

Ndula weighs almost 6,400 pounds.

Try It

Arnold’s SUV weighs about [latex]4.3[/latex] tons. Convert the weight to pounds.

Show Solution

[latex]8600[/latex] pounds

Try It

A cruise ship weighs [latex]51000[/latex] tons. Convert the weight to pounds.

Show Solution

[latex]102,000,000[/latex] pounds

Sometimes to convert from one unit to another, we may need to use several other units in between, so we will need to multiply several fractions.

Example

Juliet is going with her family to their summer home. She will be away for [latex]9[/latex] weeks. Convert the time to minutes.

Show Solution

To convert weeks into minutes, we will convert weeks to days, days to hours, and then hours to minutes. To do this, we will multiply by conversion factors of 1.

9 weeks

Write 1 as

$\frac{7 days}{1 week}, \frac{24 hours}{1 day}, \frac{60 minutes}{1 hour}$ .

Cancel common units.

Multiply.

\frac{9 \cdot 7 \cdot 24 \cdot 60 min}{1 \cdot 1 \cdot 1 \cdot 1} = 90, 720 min

Juliet will be away for 90,720 minutes.

Try It

The distance between Earth and the moon is about [latex]250,000[/latex] miles. Convert this length to yards.

Show Solution

[latex]440,000,000[/latex] yards.

Try It

A team of astronauts spends [latex]15[/latex] weeks in space. Convert the time to minutes.

Show Solution

[latex]151,200[/latex] minutes.

Example

How many fluid ounces are in [latex]1[/latex] gallon of milk?

A photograph of a milk display in a grocery store. — Figure 2 (credit: www.bluewaikiki.com, Flickr)

Show Solution

Use conversion factors to get the right units: convert gallons to quarts, quarts to pints, pints to cups, and cups to fluid ounces.

1 gallon

Multiply the measurement to be converted by 1.

\frac{1 gal}{1} \cdot \frac{4 qt}{1 gal} \cdot \frac{2 pt}{1 qt} \cdot \frac{2 C}{1 pt} \cdot \frac{8 fl oz}{1 C}

Simplify.

\frac{1 gal}{1} \cdot \frac{4 qt}{1 gal} \cdot \frac{2 pt}{1 qt} \cdot \frac{2 C}{1 pt} \cdot \frac{8 fl oz}{1 C}

Multiply.

\frac{1 \cdot 4 \cdot 2 \cdot 2 \cdot 8 fl oz}{1 \cdot 1 \cdot 1 \cdot 1 \cdot 1}

Simplify.

128 fluid ounces

There are 128 fluid ounces in a gallon.

Try It

How many cups are in [latex]1[/latex] gallon?

Show Solution

[latex]16[/latex] cups.

Try It

How many teaspoons are in [latex]1[/latex] cup?

Show Solution

[latex]48[/latex] teaspoons.

Use Mixed Units of Measurement in the U.S. System

Performing arithmetic operations on measurements with mixed units of measures requires care. Be sure to add or subtract like units.

Example

Charlie bought three steaks for a barbecue. Their weights were [latex]14[/latex] ounces, [latex]1[/latex] pound [latex]2[/latex] ounces, and [latex]1[/latex] pound [latex]6[/latex] ounces. How many total pounds of steak did he buy?

A photograph of meat being cooked on a charcoal grill. — Figure 3 (credit: Helen Penjam, Flickr)

Show Solution

We will add the weights of the steaks to find the total weight of the steaks.

Add the ounces. Then add the pounds.

Adding 1 pound and 1 pound, and then adding 2 ounces and 6 ounces

Convert 22 ounces to pounds and ounces.

Add the pounds.

2 pounds + 1 pound, 6 ounces
3 pounds, 6 ounces

Charlie bought 3 pounds 6 ounces of steak.

Try It

Laura gave birth to triplets weighing [latex]3[/latex] pounds [latex]12[/latex] ounces, [latex]3[/latex] pounds [latex]3[/latex] ounces, and [latex]2[/latex] pounds [latex]9[/latex] ounces. What was the total birth weight of the three babies?

Show Solution

[latex]9[/latex] lbs. 8 oz.

Try It

Seymour cut two pieces of crown molding for his family room that were [latex]8[/latex] feet [latex]7[/latex] inches and [latex]12[/latex] feet [latex]11[/latex] inches. What was the total length of the molding?

Show Solution

[latex]21[/latex] ft. [latex]6[/latex] in.

Example

Anthony bought four planks of wood that were each[latex]6[/latex] feet [latex]4[/latex] inches long. If the four planks are placed end-to-end, what is the total length of the wood?

The image shows 4 planks of wood placed end-to-end horizontally. Each plank is labeled 6 feet 4 inches. A line starts at the left of the first plank and runs horizontally to the right of the fourth plank. The line is labeled with the letter l to represent length. — Figure 4

Show Solution

We will multiply the length of one plank by [latex]4[/latex] to find the total length.

Multiply the inches and then the feet.

Convert 16 inches to feet.

24 feet + 1 foot 4 inches

Add the feet.

25 feet 4 inches

Anthony bought 25 feet 4 inches of wood.

Try It

Henri wants to triple his spaghetti sauce recipe, which calls for [latex]1[/latex] pound [latex]8[/latex] ounces of ground turkey. How many pounds of ground turkey will he need?

Show Solution

[latex]4[/latex] lbs. [latex]8[/latex] oz.

Try It

Joellen wants to double a solution of [latex]5[/latex] gallons [latex]3[/latex] quarts. How many gallons of solution will she have in all?

Show Solution

[latex]11[/latex] gal. [latex]2[/latex] qts.

Access the online resource below for additional instruction and practice with the American Unit Conversion:

Make Unit Conversions in the Metric System

In the metric system, units are related by powers of [latex]10[/latex]. The root words of their names reflect this relation. For example, the basic unit for measuring length is a meter. One kilometer is [latex]1000[/latex]meters; the prefix kilo- means thousand. One centimeter is [latex]\frac{1}{100}[/latex] of a meter, because the prefix centi- means one one-hundredth (just like one cent is [latex]\frac{1}{1000}[/latex] of one dollar).

The equivalencies of measurements in the metric system are shown in the table below. The common abbreviations for each measurement are given in parentheses.


Metric Measurements
Length	Mass	Volume/Capacity
$1$ kilometer (km) = $1000$ m $1$ hectometer (hm) = $100$ m $1$ dekameter (dam) = $10$ m $1$ meter (m) = $1$ m $1$ decimeter (dm) = $0.1$ m $1$ centimeter (cm) = $0.01$ m $1$ millimeter (mm) = $0.001$ m	$1$ kilogram (kg) = $1000$ g $1$ hectogram (hg) = $100$ g $1$ dekagram (dag) = $10$ g $1$ gram (g) = $1$ g $1$ decigram (dg) = $0.1$ g $1$ centigram (cg) = $0.01$ g $1$ milligram (mg) = $0.001$ g	$1$ kiloliter (kL) = $1000$ L $1$ hectoliter (hL) = $100$ L $1$ dekaliter (daL) = $10$ L $1$ liter (L) = $1$ L $1$ deciliter (dL) = $0.1$ L $1$ centiliter (cL) = $0.01$ L $1$ milliliter (mL) = $0.001$ L
$1$ meter = $100$ centimeters $1$ meter = $1000$ millimeters	$1$ gram = $100$ centigrams $1$ gram = $1000$ milligrams	$1$ liter = $100$ centiliters $1$ liter = $1000$ milliliters

To make conversions in the metric system, we will use the same technique we did in the U.S. system. Using the identity property of multiplication, we will multiply by a conversion factor of one to get to the correct units.

Have you ever run a [latex]5[/latex] k or [latex]10[/latex] k race? The lengths of those races are measured in kilometers. The metric system is commonly used in the United States when talking about the length of a race.

Example

Nick ran a [latex]10[/latex]-kilometer race. How many meters did he run?

A photograph of 8 male runners in a track race. — Figure 5 (credit: William Warby, Flickr)

Show Solution

We will convert kilometers to meters using the Identity Property of Multiplication and the equivalencies in the table above.

10 kilometers

Multiply the measurement to be converted by 1.

Write 1 as a fraction relating kilometers and meters.

$Writing 1 as a fraction relating kilometers and meters$

Simplify.

Multiply.

10,000 m

Nick ran 10,000 meters.

Try It

Sandy completed her first [latex]5[/latex]-km race. How many meters did she run?

Show Solution

[latex]5000[/latex] m

Try It

Herman bought a rug [latex]2.5[/latex] meters in length. How many centimeters is the length?

Show Solution

[latex]250[/latex] cm

Example

Eleanor’s newborn baby weighed [latex]3200[/latex] grames. How many kilograms did the baby weigh?

Show Solution

We will convert grams to kilograms.

Multiply the measurement to be converted by 1.

Write 1 as a fraction relating kilograms and grams.

$Writing 1 as a fraction relating kilograms and gram$

Simplify.

Multiply.

Divide.

3.2 kilograms

The baby weighed

$3.2$ kilograms.

Try It

Kari’s newborn baby weighed [latex]2800[/latex] grams. How many kilograms did the baby weigh?

Show Solution

[latex]2.8[/latex] kilograms

Try It

Anderson received a package that was marked [latex]4500[/latex] grams. How many kilograms did this package weigh?

Show Solution

[latex]4.5[/latex] kilograms

Since the metric system is based on multiples of ten, conversions involve multiplying by multiples of ten. In Decimal Operations, we learned how to simplify these calculations by just moving the decimal. To multiply by [latex]10, 100[/latex], or [latex]1000[/latex], we move the decimal to the right [latex]1, 2,[/latex] or [latex]3[/latex] places, respectively. To multiply by [latex]0.1, 0.01,[/latex], or [latex]0.001[/latex], we move the decimal to the left [latex]1, 2[/latex], or [latex]3[/latex] places respectively.

We can apply this pattern when we make measurement conversions in the metric system.

Below, we changed [latex]3200[/latex] grams to kilograms by multiplying by [latex]\frac{1}{1000}[/latex] or [latex]0.001[/latex]. This is the same as moving the decimal [latex]3[/latex] places to the left.

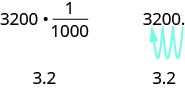
Multiplying 3200 by 1 over 1000 gives 3.2. Notice that the answer, 3.2, is similar to the original value, 3200, just with the decimal moved three places to the left.

Example

Convert:ⓐ 350 liters to kilolitersⓑ 4.1 liters to milliliters.

Show Solution

ⓐ We will convert liters to kiloliters. We know that 1 kiloliter = 1000 liters.

350 L

Multiply by 1, writing 1 as a fraction relating liters to kiloliters.

$Multiply 350 L by 1, writing 1 as a fraction relating liters to kiloliters.$

Simplify.

Move the decimal 3 units to the left.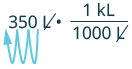

0.35 kL

ⓑ We will convert liters to milliliters. We know that 1 liter = 1000 milliliters.

4.1 L

Multiply by 1, writing 1 as a fraction relating milliliters to liters.

$Multiply 4.1 L by 1, writing 1 as a fraction relating milliliters to liters$

Simplify.

Move the decimal 3 units to the left.

4100 mL

Try It

Convert: ⓐ 7.25 L to kL ⓑ 6.3 L to mL.

Show Solution

ⓐ [latex]0.00725[/latex] kL ⓑ [latex]6300[/latex]mL.

Try It

Convert: ⓐ 350 hL to L ⓑ 4.1 L to cL.

Show Solution

ⓐ [latex]35,000[/latex] L ⓑ [latex]410[/latex]cL.

Access the online resource below for additional instruction and practice with Metric Unit Conversion:

Use Mixed Units of Measurement in the Metric System

Performing arithmetic operations on measurements with mixed units of measures in the metric system requires the same care we used in the U.S. system. But it may be easier because of the relation of the units to the powers of 10. We still must make sure to add or subtract like units.

Example

Ryland is 1.6 meters tall. His younger brother is 85 centimeters tall. How much taller is Ryland than his younger brother?

Show Solution

We will subtract the lengths in meters. Convert 85 centimeters to meters by moving the decimal 2places to the left; 85 cm is the same as 0.85 m.

Now that both measurements are in meters, subtract to find out how much taller Ryland is than his brother.

\begin{matrix} 1.60 m \\ \underset{_______}{−0.85 m} \\ 0.75 m \end{matrix}

Ryland is 0.75 meters taller than his brother.

Try It

Mariella is 1.58 meters tall. Her daughter is 75 centimeters tall. How much taller is Mariella than her daughter? Write the answer in centimeters.

Show Solution

[latex]83[/latex] cm

Try It

The fence around Hank’s yard is 2 meters high. Hank is 96 centimeters tall. How much shorter than the fence is Hank? Write the answer in meters.

Show Solution

[latex]1.04[/latex] m

Example

Dena’s recipe for lentil soup calls for 150 milliliters of olive oil. Dena wants to triple the recipe. How many liters of olive oil will she need?

Show Solution

We will find the amount of olive oil in milliliters then convert to liters.

Triple 150 mL

Translate to algebra.

3 \cdot 150 mL

Multiply.

450 mL

Convert to liters.

450 mL \cdot \frac{0.001 L}{1 mL}

Simplify.

0.45 L

Dena needs 0.45 liter of olive oil.

Try It

A recipe for Alfredo sauce calls for 250 milliliters of milk. Renata is making pasta with Alfredo sauce for a big party and needs to multiply the recipe amounts by 8 . How many liters of milk will she need?

Show Solution

[latex]2[/latex] L

Try It

To make one pan of baklava, Dorothea needs 400 grams of filo pastry. If Dorothea plans to make 6 pans of baklava, how many kilograms of filo pastry will she need?

Show Solution

[latex]2.4[/latex] Kg

Convert Between U.S. and Metric Systems of Measurement

Many measurements in the United States are made in metric units. A drink may come in $2-liter$ bottles, calcium may come in $500-mg$ capsules, and we may run a $5-K$ race. To work easily in both systems, we need to be able to convert between the two systems. Table below shows some of the most common conversions.

Table
Conversion Factors Between U.S. and Metric Systems
Length	Weight	Volume
1 in = 2.54 cm 1 ft = 0.305 m 1 yd = 0.914 m 1 mi = 1.61 km 1 m = 3.28 ft	$0.45$ kg 1 oz = 28 g 1 kg = 2.2 lb	$1$ 1 fl oz = 30 mL 1 L = 1.06 qt

We make conversions between the systems just as we do within the systems—by multiplying by unit conversion factors.

Example

Lee’s water bottle holds $500$ mL of water. How many fluid ounces are in the bottle? Round to the nearest tenth of an ounce.

Show Solution

500 mL

Multiply by a unit conversion factor relating mL and ounces.

[latex]500 \text{mL} \cdot \frac{1 \text{fl oz}}{30 \text{mL}}[/latex]

Simplify.

[latex]\frac{500 \text{fl oz}}{30}[/latex]

Divide.

16.7 fl. oz.

The water bottle holds 16.7 fluid ounces.

Try It

How many quarts of soda are in a $2-liter$ bottle?

Show Solution

[latex]2.12[/latex] quarts

Try It

How many liters are in $4$ quarts of milk?

Show Solution

[latex]3.8[/latex] iters

The conversion factors in the table above are not exact, but the approximations they give are close enough for everyday purposes. In the example above, we rounded the number of fluid ounces to the nearest tenth.

Example

Soleil lives in Minnesota but often travels in Canada for work. While driving on a Canadian highway, she passes a sign that says the next rest stop is in 100 kilometers. How many miles until the next rest stop? Round your answer to the nearest mile.

Show Solution

100 kilometers

Multiply by a unit conversion factor relating kilometers and miles.

[latex]100 \text{ kilometers} \cdot \frac{1 \text{mile}}{1.61 \text{ kilometers}}[/latex]

[latex]100 \cdot \frac{1 \text{mi}}{1.61 \text{ km}}[/latex]

Simplify.

[latex]\frac{100 \text{mi}}{1.61}[/latex]

Divide.

[latex]62 \text {mi}[/latex]

It is about 62 miles to the next rest stop.

Try It

The height of Mount Kilimanjaro is $5,895$ meters. Convert the height to feet. Round to the nearest foot.

Show Solution

[latex]19,336[/latex] ft

Try It

The flight distance from New York City to London is $5,586$ kilometers. Convert the distance to miles. Round to the nearest mile.

Show Solution

[latex]3,470[/latex] mi

Access the online resource below for additional instruction and practice with the American and Metric Unit Conversion:

Convert Between Fahrenheit and Celsius Temperatures

Have you ever been in a foreign country and heard the weather forecast? If the forecast is for $22 °C .$ What does that mean?

The U.S. and metric systems use different scales to measure temperature. The U.S. system uses degrees Fahrenheit, written $°F .$ The metric system uses degrees Celsius, written $°C .$ The Figure below shows the relationship between the two systems.

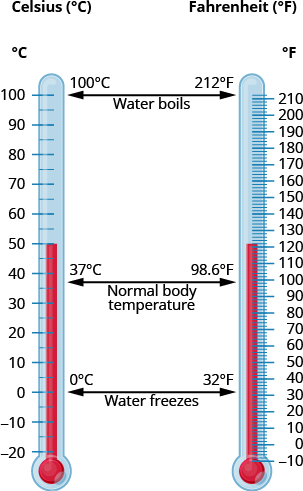
On the left side of the figure is a thermometer marked in degrees Celsius. The bottom of the thermometer begins with negative 20 degrees Celsius and ranges up to 100 degrees Celsius. There are tick marks on the thermometer every 5 degrees with every 10 degrees labeled. On the right side is a thermometer marked in degrees Fahrenheit. The bottom of the thermometer begins with negative 10 degrees Fahrenheit and ranges up to 212 degrees Fahrenheit. There are tick marks on the thermometer every 2 degrees with every 10 degrees labeled. Between the thermometers there is an arrow pointing on the left to 0 degrees Celsius and on the right to 32 degrees Fahrenheit. This is the temperature at which water freezes. Another arrow points on the left to 37 degrees Celsius and on the right to 98.6 degrees Fahrenheit. This is normal body temperature. A third arrow points on the left to 100 degrees Celsius and on the right to 212 degrees Fahrenheit. This is the temperature at which water boils. — Figure 6 A temperature of 37°C is equivalent to 98.6°F.

If we know the temperature in one system, we can use a formula to convert it to the other system.

Prime Factorization

To convert from Fahrenheit temperature, F, to Celsius temperature, C, use the formula

[latex]C = \frac{5}{9} ( F-32)[/latex]

To convert from Celsius temperature, C, to Fahrenheit temperature, F, use the formula

[latex]F = \frac{9}{5} C + 32[/latex]

Example

Convert $50 °F$ into degrees Celsius.

Show Solution

We will substitute $50 °F$ into the formula to find C.

Use the formula for converting °F to °C

[latex]C= \frac{5}{9} (F-32)[/latex]

Substitute 50 for F.

[latex]C= \frac{5}{9} (50-32)[/latex]

Simplify in parentheses.

[latex]C= \frac{5}{9} (18)[/latex]

Multiply.

[latex]C=10[/latex]

A temperature of 50°F is equivalent to 10°C.

Try It

Convert the Fahrenheit temperatures to degrees Celsius: $59 °F .$

Show Solution

[latex]15[/latex] $59 °F .$

Try It

Convert the Fahrenheit temperatures to degrees Celsius: $41 °F .$

Show Solution

[latex]5[/latex] $59 °F .$

Example

The weather forecast for Paris predicts a high of $20 °C.$ Convert the temperature into degrees Fahrenheit.

Show Solution

We will substitute $20 °C$ into the formula to find $F .$

Use the formula for converting °F to °C

[latex]F= \frac{9}{5}C+32[/latex]

Substituting [latex]20[/latex] for C

[latex]F= \frac{9}{5} (20)+32[/latex]

Multiply.

F = 36 + 32

Add.

F = 68

So 20°C is equivalent to 68°F.

Try It

Convert the Celsius temperatures to degrees Fahrenheit:

The temperature in Helsinki, Finland was $15 °C .$

Show Solution

[latex]59[/latex] $10 °C .$

Try It

Convert the Celsius temperatures to degrees Fahrenheit:

The temperature in Sydney, Australia was $10 °C .$

Show Solution

[latex]50[/latex] $10 °C .$

Access the online resource below for additional instruction and practice with the Conversion of Temperature from Celsius to Fahrenheit:

Access the online resource below for additional instruction and practice with the Conversion of Temperature from Fahrenheit to Celsius :

The Role of Units in Measurement

Scientists make observations and ask basic questions. For example, how big is an object? How much mass does it have? How far did it travel? To answer these questions, they make measurements with various instruments (e.g., meter stick, balance, stopwatch, etc.).

The measurements of physical quantities are expressed in terms of units, which are standardized values. For example, the length of a race, which is a physical quantity, can be expressed in meters (for sprinters) or miles (for marathon runners). Without standardized units, it would be extremely difficult for scientists to express and compare measured values in a meaningful way (Figure 1).

A person is standing in front of a map that has cable as units. The person is confused and is wondering how big a cable is. — Figure 7. Distances given in unknown units are maddeningly useless.

Some Common Units

Measured Quantity

Units

Time

second (s), minute (min), hour (h), year (yr), etc.

Length

meter (m), inch (in), foot (ft), mile (mi), etc.

Mass or Weight

kilogram (kg), ounce (oz), pound (lb), etc.

Table 1 Some Common Units

The Metric System

The metric system is a decimal system of measurement which is based on a set of fundamental units including the meter, the second, and the kilogram. Most of the world uses the metric system. However, the United States is one of the few countries which also uses U.S. customary units, which are sometimes referred to as the imperial system.

The metric system is convenient because conversions between metric units can be done simply by moving the decimal place of a number. This is because the metric prefixes are sequential powers of 10. There are 100 centimeters in a meter, 1000 meters in a kilometer, and so on. In nonmetric systems, such as U.S. customary units, the relationships are less simple—there are 12 inches in a foot, 5,280 feet in a mile, 4 quarts in a gallon, and so on.

Another advantage of the metric system is that the same unit can be used over extremely large ranges of values simply by switching to the most appropriate metric prefix. For example, distances in meters are suitable for building construction, but kilometers are used to describe road construction. Therefore, with the metric system, there is no need to invent new units when measuring very small or very large objects—you just have to move the decimal point (and use the appropriate prefix). Table 1 gives the metric prefixes and symbols used to denote the different various factors of 10 in the metric system.

Metric Prefixes for Powers of 10 and Their Symbols

Prefix

Symbol

Value

Example Name

Example Symbol

Example Value

Example Description

kilo

k

10³

Kilometer

km

10³ m

About 6/10 mile

hecto

h

10²

Hectoliter

hL

10² L

26 gallons

deka

da

10¹

Dekagram

dag

10¹ g

Teaspoon of butter

10⁰ (=1)

deci

d

10^–1

Deciliter

dL

10^–1 L

Less than half a soda

centi

c

10^–2

Centimeter

cm

10^–2 m

Fingertip thickness

milli

m

10^–3

Millimeter

mm

10^–3 m

Flea at its shoulder

Table 2 Metric Prefixes and Their Symbols

Conversion Factors

It is often necessary to convert from one type of unit to another. For example, if you are reading a European cookbook in the United States, some quantities may be expressed in liters and you need to convert them to cups. A Canadian tourist driving through the United States might want to convert miles to kilometers, to have a sense of how far away his next destination is. A doctor in the United States might convert a patient’s weight in pounds to kilograms.

Unit equivalences tell you how many of one unit are equivalent to exactly one of another unit. For example, 1 foot is equivalent to 12 inches, 1000 milliliters are equivalent to one liter, and 1 minute is equivalent to 60 seconds. Several commonly used equivalences are given in Table 3.

Common Equivalences

Length

Volume

Mass

1 m = 1.0936 yd

1 L = 1.0567 qt

1 kg = 2.2046 lb

1 in. = 2.54 cm (exact)

1 gal = 3.7854 L

1 lb = 453.59 g

1 km = 0.62137 mi

1 ft³ = 28.317 L

1 (avoirdupois) oz = 28.349 g

1 mi = 1609.3 m

1 tbsp = 14.787 mL

1 (troy) oz = 31.103 g

Table 3 Common Equivalences

A ratio of two equivalent quantities expressed with different measurement units can be used as a unit conversion factor. A conversion factor is simply a fraction which equals 1. You can multiply any number by 1 and get the same value. When you multiply a number by a conversion factor, you are simply multiplying it by one. For example, the following are conversion factors:

[latex]\frac{1 \text{ foot}}{12 \text{ inches}} = 1[/latex] to convert inches to feet,
[latex]\frac{1 \text{ liter}}{1000 \text{ milliliters}} = 1[/latex] to convert milliliters to liters, and
[latex]\frac{1 \text{ minute}}{60 \text{ seconds}} = 1[/latex] to convert seconds to minutes.

Example

Find a unit conversion factor between centimeters and inches.

Solution

The lengths of 2.54 cm and 1 in. are equivalent (by definition), and so a unit conversion factor may be derived from the ratio:

[latex]\frac{2.54\text{ cm}}{1\text{ in}} \left(2.54\text{ cm}=1\text{ in}\right) \text{ or } 2.54\frac{\text{cm}}{\text{in}}[/latex]

The previous conversion factor is used to convert from inches to centimeters. Another conversion factor can also be formed from these two equivalent lengths:

[latex]\frac{1\text{ in}}{2.54\text{ cm}}\left(1\text{ in}=2.54\text{ cm}\right)\text{ or }0.394\frac{\text{in}}{\text{cm}}[/latex]

This conversion factor is used for converting centimeters to inches.

Try It

Find two unit conversion factors between pounds and grams.

Solution

[latex]\frac{1\text{ lb}}{453.59\text{ g}}\text{ and }\frac{453.59\text{ g}}{1\text{ lb}}[/latex]

Try It

Find two unit conversion factors between tablespoons and milliliters.

Solution

[latex]\frac{1\text{ tbsp}}{14.787\text{ mL}}\text{ and }\frac{14.787\text{ mL}}{1\text{ tbsp}}[/latex]

Converting Between Units

When a quantity (such as distance in inches) is multiplied by an appropriate unit conversion factor, the quantity is converted to an equivalent value with different units (such as distance in centimeters). The numbers of these two quantities are multiplied to yield the number of the product quantity, whereas the units are multiplied to yield the units of the final answer. You can use this method to convert between any types of unit, including between the U.S. customary system and metric system. Notice also that, although you can multiply and divide units algebraically, you cannot add or subtract different units. An expression like 10 km + 5 kg makes no sense. Even adding two lengths in different units, such as 10 km + 20 m does not make sense. You express both lengths in the same unit.

How To

Convert Between Units

Step 1. Identify the starting unit and the target unit.

Step 2. Find a unit equivalence between the two units. (Sometimes using an intermediate unit is helpful.)

Step 3. Determine the conversion factor that will eliminate the starting unit and leave you with the target unit.

Step 4. Multiply the measurement by the conversion factor.

Example

The mass of a competition frisbee is 125 g. Convert its mass to ounces using the unit conversion factor derived from the relationship 1 oz = 28.349 g (Table 3).

Solution

Step 1. Identify the starting unit and the target unit.	The measurement is in grams and we would like to convert to ounces.
Step 2. Find a unit equivalence between the two units.	The equivalence 1 oz = 28.349 g is given in the problem.
Step 3. Determine the correct conversion factor.	[latex]\frac{1\text{ oz}}{28.349\text{ g}} \text{ or } \frac{28.349\text{ g}}{1\text{ oz}}[/latex]
	The correct unit conversion factor is the ratio that cancels the units of grams and leaves ounces.
Step 4. Multiply the measurement by the conversion factor.	[latex]\begin{aligned}x\text{ oz}&=125\text{ g}\times\frac{1\text{ oz}}{28.349\text{ g}}\\&=\frac{125}{28.349}\text{ oz}\\&=4.41\text{ oz}\end{aligned}[/latex]
	Answer: The mass of the competition frisbee is 4.41 ounces.

Try It

The length of an American football field is 100 yards, excluding the end zones. Convert this length to meters using a unit conversion factor derived from the relationship 1 m = 1.0936 yd. Round to the nearest 0.1 m.

Solution

91.4 m

Try It

The month of March has 31 days. Use a unit conversion factor derived from the fact that there are 24 hours in one day to determine how many hours are in the month of March.

Solution

744 hrs

Example

A basketball player’s vertical jump is 34 inches high. How many centimeters is this?

Solution

Step 1. Identify the starting unit and the target unit.

The measurement is in inches and we want to convert it to feet.

Step 2. Find a unit equivalence between the two units.

From Table 3, we know that 1 inch is equivalent to 2.54 centimeters.

Step 3. Determine the correct conversion factor.

[latex]\frac{2.54\text{ cm}}{1\text{ in}}[/latex] cancels inches and leaves centimeters.

Step 4. Multiply the measurement by the conversion factor.

[latex]34\text{ in} \times \frac{2.54\text{ cm}}{1\text{ in}}=86\text{ cm.}[/latex]

The player’s vertical jump is 86 cm high.

Try It

The gas tank of a Honda Civic holds 12.4 gallons of gas. How many liters can it hold?

Solution

46.9 L

Try It

Genevieve’s doctor tells her that she weighs 65.8 kilograms. How many pounds does Genevieve weigh?

Solution

145 lbs

Combining Conversion Factors

Sometimes, to convert between two units, it is easier to use more than one conversion factor in your calculations. Each successive conversion factor will cancel the units introduced by the previous conversion factor, and the final conversion factor will convert your result into the desired units. In the next example, we will use a conversion factor to change hours to minutes and another conversion factor to change minutes to seconds. This can be done in one calculation.

Example

Convert 1 hour to seconds.

Solution

Step 1. Identify the starting unit and the target unit.

The measurement is in hours and we want to convert it to seconds.

Step 2. Find a unit equivalence between the two units.

We have equivalences 1 hour = 60 minutes and 1 minute = 60 seconds.

Step 3. Determine the correct conversion factors.

[latex]\frac{60 \text{ min}}{1 \text{ h}}[/latex] cancels hours and leaves minutes, and [latex]\frac{60 \text{ s}}{1 \text{ min}}[/latex] cancels minutes to leave seconds.

Step 4. Multiply the measurement by the conversion factors.

[latex]1\text{ h}\times\frac{60\text{ min}}{1\text{ h}}\times\frac{60\text{ s}}{1\text{ min}}=3600\text{ s}.[/latex]

1 hour is equal to 3600 seconds.

Try It

Joe calculates that he has a cubic foot of milk in his refrigerator. How many quarts is this? Round to the nearest integer.

Solution
30 quarts

Try It

Manuela’s necklace contains 1.3 troy ounces of gold. How many kilograms of gold is this?

Solution

0.0404 kg

Converting Area and Volume

Sometimes, a measurement may be given in square units (area) or cubic units (volume). In these cases, each instance of the unit needs to be converted separately. For example, one square foot contains 144 square inches – the length in feet is converted to a length in inches, and the width in feet is also converted to inches, as seen in the following example.

Example

A sheet of cardboard has an area of 6 square feet. How many square inches is this?

Solution

Step 1. Identify the starting unit and the target unit.

The measurement is in [latex]\text{ft}\cdot\text{ft}[/latex] and we will convert to [latex]\text{in}\cdot\text{in}[/latex].

Step 2. Find a unit equivalence between the two units.

1 foot = 12 inches

Step 3. Determine the correct conversion factor.

[latex]\frac{12\text{ in}}{1\text{ ft}}[/latex] cancels feet and leaves inches. We will need to multiply by this conversion factor twice.

Step 4. Multiply the measurement by the conversion factor.

[latex]6 \text{ ft}\cdot\text{ft} \times\frac{12 \text{ in}}{1 \text{ ft}}\times \frac{12 \text{ in}}{1 \text{ ft}} = 864 \text{ in}^2[/latex]

The cardboard has an area of 864 square inches.

Try It

A 12-ounce can of soda contains 0.355 L of liquid. If 1 L = 1 dm³, how many cubic centimeters of liquid are in the can?

Solution

355 cm³

Try It

The area of a wall to be painted is 142,350 square inches. How many square feet is this?

Solution

988.5 ft²

Rate Conversions

It is often the case that a quantity of interest may not be easy (or even possible) to measure directly but instead must be calculated from other directly measured properties and appropriate mathematical relationships. A rate is a quantity which is computed from measurements in two or more different units.

The units of rates give us a hint as to how they are calculated. Table 4 gives some examples of rates and the calculations to determine them from direct measurements.

Some Common Rates

Rate

Calculation

Speed in miles per hour

Divide the length (in miles) by the time (in hours) needed to travel that distance.

Density in g/mL

Divide the mass (in grams) of the substance by its volume (in mL).

Fuel efficiency in miles per gallon

Divide the number of miles driven by the number of gallons of gasolines used.

Table 4 Some Common Rates

As you have seen, the method of multiplying quantities by conversion factors can be applied to computations ranging from simple unit conversions to more complex, multi-step conversions. Rate conversions are unit conversions involving several different quantities. When units are to be converted in a case like this, careful unit conversions are required for each unit involved.

How To

Carry Out Rate Conversions

Step 1. Calculate the quantity from the given measurements if necessary.

Step 2. Identify all of the units involved in the quantity.

Step 3. Identify the units that need to be converted and the target units.

Step 4. Determine appropriate conversion factors.

Step 5. Multiply the quantity by conversion factors to convert the starting combination of units to a combination of the desired units.

Example

Suppose that you drive the 10 km from your university to home in 20 min. Calculate your average speed (a) in kilometers per hour (km/h) and (b) in meters per second (m/s).

Solution for (a)

Step 1. Calculate the quantity from the given measurements.

Average speed is distance traveled divided by time of travel.

[latex]\text{average speed}=\frac{10\text{ km}}{20\text{ min}}=0.5\frac{\text{km}}{\text{min}}[/latex]

Step 2. Identify the units involved in the quantity.

The units present in the average speed are kilometers and minutes.

Step 3. Identify the units that need to be converted and the target units.

We want to give the speed in kilometers per hour, so we need to change minutes to hours.

Step 4. Determine appropriate conversion factors.

[latex]\frac{60\text{ min}}{\text{hr}}[/latex] cancels minutes from the denominator and leaves hours.

Step 5. Multiply the quantity by the conversion factor.

[latex]\frac{0.5\text{ km}}{\text{min}}\times\frac{60\text{ min}}{\text{hr}}=30\frac{\text{km}}{\text{ hr}}[/latex]

The average speed is 30 kilometers per hour.

Solution for (b)

There are several ways to convert the average speed into meters per second.

1. Start with the answer to (a) and convert km/h to m/s.

Step 1. Calculate the quantity from the given measurements.

The quantity is 30 kilometers per hour.

Step 2. Identify the units involved in the quantity.

The units are kilometers and hours.

Step 3. Identify the units that need to be converted and the target units.

We need to change kilometers to meters and hours to seconds.

Step 4. Determine appropriate conversion factors.

[latex]\frac{1000\text{ m}}{\text{km}}[/latex] cancels kilometers from the numerator and leaves meters.

[latex]\frac{1\text{ h}}{3600\text{ s}}[/latex] cancels hours from the denominator and leaves seconds.

Step 5. Multiply the quantity by the conversion factors.

[latex]\frac{30\text{ km}}{\text{h}}\times\frac{1000\text{ m}}{\text{km}}\times\frac{1\text{ h}}{3600\text{ s}}=8.33 \text{ m/s}[/latex]

The average speed is 8.33 meters per second.

2. If we had started with 0.5 km/min instead, we would have needed different conversion factors, but the answer would have been the same: 8.33 m/s.

Try It

If it takes a ball 8 seconds to fall 32 meters, what is its average speed in miles per hour?

Solution

8.9 mph

Try It

Sha’Carri Richardson can run 100 meters in 10.65 seconds. Can she outrun a car traveling at 20 miles per hour?

Solution

Yes, she can run at 21 mph.

Example

An American is driving 103 km/h in a Canadian vehicle. How many miles per hour is this?

Solution

Step 1. Calculate the quantity from the given measurements.

The quantity is 103 km/h.

Step 2. Identify the units involved in the quantity.

The units are kilometers and hours.

Step 3. Identify the units to be converted and the target units.

We need to change kilometers to miles.

Step 4. Determine an appropriate conversion factor.

[latex]\frac{1\text{ mi}}{1.609\text{ km}}[/latex] cancels kilometers and leaves miles.

Step 5. Multiply the quantity by the conversion factor.

[latex]\frac{103\text{ km}}{\text{h}}\times\frac{1\text{ mi}}{1.609\text{ km}}=64\text{ mi/h}[/latex]

103 km/h is equivalent to 64 mph.

Try It

An object must travel at least 11.2 km/s in order to escape Earth’s gravity and travel to outer space. How many miles per hour is this?

Solution

25,059 mph

Try It

The speed limit on some interstate highways is roughly 100 km/h. How many miles per hour is this?

Solution

62.1 mph

Example

What is the density of common antifreeze in units of g/mL? A 4-qt sample of the antifreeze weighs 9.26 lb.

Solution

Step 1. Calculate the quantity from the given measurements.

The density can be given in g/mL, so we need to divide the mass by the volume.

[latex]\frac{9.26\text{ lb}}{4\text{ qt}}=2.315\frac{\text{lb}}{\text{qt}}[/latex]

Step 2. Identify the units involved in the quantity.

The units are pounds and quarts.

Step 3. Identify the units to be converted and the target units.

We need to convert pounds to grams and quarts to milliliters.

Step 4. Determine the appropriate conversion factors.

[latex]\frac{453.59\text{ g}}{1\text{ lb}}[/latex] cancels pounds in the numerator and leaves grams.

[latex]\frac{1.0567\text{ qt}}{1\text{ L}}[/latex] cancels quarts in the denominator and leaves liters, and [latex]\frac{1\text{ L}}{1000\text{ mL}}[/latex] cancels liters to leave milliliters.

Step 5. Multiply the quantity by the conversion factors.

[latex]\frac{2.315\text{ lb}}{1\text{ qt}}\times\frac{453.59\text{ g}}{1\text{ lb}}\times\frac{1.0567\text{ qt}}{1\text{ L}}\times\frac{1000\text{ mL}}{1\text{ L}}=1.11 \text{g/mL}[/latex]

The density of common antifreeze is 1.11 grams per milliliter.

Try It

What is the volume in liters of 1 oz, given that 1 L = 1.0567 qt and 1 qt = 32 oz?

Solution

0.02957 L

Try It

An unknown metal weighs 219 pounds and displaces 5 quarts of water. If aluminum has a density of 2.7 g/mL, iron 7.96 g/mL, mercury 13.6 g/mL, and gold 19.3 g/mL, which substance are you most likely to have?

Solution

18.8 g/mL is closest to the density of gold.

Example

While being driven from Philadelphia to Atlanta, a distance of about 1250 km, a 2014 Lamborghini Aventador Roadster uses 213 L gasoline.

(a) What (average) fuel economy, in miles per gallon, did the Roadster get during this trip?

(b) If gasoline costs $3.80 per gallon, what was the fuel cost for this trip?

Solution

Step 1. Calculate the quantity from the given measurements.

The fuel economy is in miles per gallon, so we divide the distance traveled by the volume of gasoline used.

[latex]\frac{1250\text{ km}}{213\text{ L}}=5.869\text{ km/L}[/latex]

Step 2. Identify the units involved in the quantity.

The units are kilometers and liters.

Step 3. Identify the units to be converted and the target units.

We need to convert kilometers to miles and liters to gallons.

Step 4. Determine the appropriate conversion factors.

[latex]\frac{0.62137\text{ mi}}{1\text{ km}}[/latex] cancels kilometers and leaves miles in the numerator.

[latex]\frac{1\text{ L}}{1.0567\text{ qt}}[/latex] converts liters to quarts, and [latex]\frac{4\text{ qt}}{1\text{ gal}}[/latex] cancels quarts and leaves gallons in the denominator.

Step 5. Multiply the quantity by the conversion factors.

[latex]\frac{5.869\text{ km}}{\text{L}}\times\frac{0.62137\text{ mi}}{1\text{ km}}\times\frac{1\text{ L}}{1.0567\text{ qt}}\times\frac{4\text{ qt}}{1\text{ gal}}=13.8\text{ mi/gal}[/latex]

The average fuel economy was 13.8 mpg.

Solution

This calculation requires us to multiply a volume by a rate to end up with a cost.

Step 1. Calculate the quantity from the given measurements.

The quantity is 213 L.

Step 2. Identify the units involved in the quantity.

The units are liters.

Step 3. Identify the units to be converted and the target units.

We have a quantity in liters and we need to change it to a quantity in dollars.

Step 4. Determine the appropriate conversion factors and rate.

[latex]\frac{1.0567\text{ qt}}{1\text{ L}}[/latex] cancels liters and leaves quarts, and [latex]\frac{1\text{ gal}}{4\text{ qts}}[/latex] cancels quarts to leave gallons.

The rate we have is that gasoline costs [latex]\frac{3.80\text{ dollars}}{1\text{ gal}}[/latex], which will cancel gallons and leave dollars.

Step 5. Multiply the quantity by the conversion factors and rate.

[latex]213\text{ L}\times\frac{1.0567\text{ qt}}{1\text{ L}}\times\frac{1\text{ gal}}{4\text{ qt}}\times\frac{3.80\text{ dollars}}{1\text {gal}}=$214[/latex]

The trip will cost $214.

Try It

You would like to drive your Toyota Corolla from Houston to Chicago, a distance of about 1100 miles, to visit a friend. Your car gets 38 miles per gallon on the highway, and one tank of gas holds 13.2 gallons. How many tanks of gas will it take for the trip?

Solution

2.2 tanks

Try It

A Toyota Prius Hybrid uses 59.7 L gasoline to drive from San Francisco to Seattle, a distance of 1300 km.

(a) What (average) fuel economy, in miles per gallon, did the Prius get during this trip?

(b) If gasoline costs $3.90 per gallon, what was the fuel cost for this trip?

Solution

(a) 51 mpg; (b) $62

Key Concepts

Prefix	Symbol	Value	Example Name	Example Symbol	Example Value	Example Description

kilo	k	10³	Kilometer	km	10³ m	About 6/10 mile
hecto	h	10²	Hectoliter	hL	10² L	26 gallons
deka	da	10¹	Dekagram	dag	10¹ g	Teaspoon of butter
		10⁰ (=1)
deci	d	10^–1	Deciliter	dL	10^–1 L	Less than half a soda
centi	c	10^–2	Centimeter	cm	10^–2 m	Fingertip thickness
milli	m	10^–3	Millimeter	mm	10^–3 m	Flea at its shoulder

Table 2 Metric Prefixes and Their Symbols

Length	Volume	Mass
1 m = 1.0936 yd	1 L = 1.0567 qt	1 kg = 2.2046 lb
1 in. = 2.54 cm (exact)	1 gal = 3.7854 L	1 lb = 453.59 g
1 km = 0.62137 mi	1 ft³ = 28.317 L	1 (avoirdupois) oz = 28.349 g
1 mi = 1609.3 m	1 tbsp = 14.787 mL	1 (troy) oz = 31.103 g

Table 3 Common Equivalences

Convert Between Units

Step 1. Identify the starting unit and the target unit.
Step 2. Find a unit equivalence between the two units. (Sometimes using an intermediate unit is helpful.)
Step 3. Determine the conversion factor that will eliminate the starting unit and leave you with the target unit.
Step 4: Multiply the measurement to be converted by 1; write 1 as a fraction relating the units given and the units needed.
Step 5: Multiply.
Step 6: Simplify the fraction, performing the indicated operations and removing the common units.

Carry Out Rate Conversions

Step 1. Identify all of the units involved in the measurement.
Step 2. Identify the units that need to be converted.
Step 3. Determine appropriate conversion factors.
Step 4. Multiply the measurement by conversion factors to convert the starting combination of units to a combination of the desired units.

Section Exercises

Make Unit Conversions in the U.S. System

In the following exercises, convert the units.

1. A floor tile is $2$ feet wide. Convert the width to inches.

Show Solution

24 inches.

2. A ribbon is $18$ inches long. Convert the length to feet.

3. Carson is $45$ inches tall. Convert his height to feet.

Show Solution

3.75 feet.

4. Jon is $6$ feet $4$ inches tall. Convert his height to inches.

5. Faye is $4$ feet $10$ inches tall. Convert her height to inches.

Show Solution

58 inches.

6. A football field is $160$ feet wide. Convert the width to yards.

7. On a baseball diamond, the distance from home plate to first base is $30$ yards. Convert the distance to feet.

Show Solution

90 feet.

8. Ulises lives $1.5$ miles from school. Convert the distance to feet.

9. Denver, Colorado, is $5,183$ feet above sea level. Convert the height to miles.

Show Solution

0.98 miles.

10. A killer whale weighs $4.6$ tons. Convert the weight to pounds.

11. Blue whales can weigh as much as $150$ tons. Convert the weight to pounds.

Show Solution

300,000 pounds.

12. An empty bus weighs $35,000$ pounds. Convert the weight to tons.

13. At take-off, an airplane weighs $220,000$ pounds. Convert the weight to tons.

Show Solution

110 tons.

14. The voyage of the Mayflower took $2$ months and $5$ days. Convert the time to days (30 days = 1 month).

15. Lynn’s cruise lasted $6$ days and $18$ hours. Convert the time to hours.

Show Solution

162 hours.

16. Rocco waited $1 \frac{1}{2}$ hours for his appointment. Convert the time to seconds.

17. Misty’s surgery lasted $2 \frac{1}{4}$ hours. Convert the time to seconds.

Show Solution

8100 seconds.

18. How many teaspoons are in a pint?

19. How many tablespoons are in a gallon?

Show Solution

256 tablespoons.

20. JJ’s cat, Posy, weighs $14$ pounds. Convert her weight to ounces.

21. April’s dog, Beans, weighs $8$ pounds. Convert his weight to ounces.

Show Solution

128 ounces.

22. Baby Preston weighed $7$ pounds $3$ ounces at birth. Convert his weight to ounces.

23. Baby Audrey weighed $6$ pounds $15$ ounces at birth. Convert her weight to ounces.

Show Solution

111 ounces.

24. Crista will serve $20$ cups of juice at her son’s party. Convert the volume to gallons.

25. Lance needs $500$ cups of water for the runners in a race. Convert the volume to gallons.

Show Solution

31.25 inches.

Use Mixed Units of Measurement in the U.S. System

In the following exercises, solve and write your answer in mixed units.

26. Eli caught three fish. The weights of the fish were $2$ pounds $4$ ounces, $1$ pound $11$ ounces, and $4$ pounds $14$ ounces. What was the total weight of the three fish?

27. Judy bought $1$ pound $6$ ounces of almonds, $2$ pounds $3$ ounces of walnuts, and $8$ ounces of cashews. What was the total weight of the nuts?

Show Solution

4 lbs. 1 oz.

28. One day Anya kept track of the number of minutes she spent driving. She recorded trips of $45, 10, 8, 65, 20, and 35 minutes.$ How much time (in hours and minutes) did Anya spend driving?

29. Last year Eric went on $6$ business trips. The number of days of each was $5, 2, 8, 12, 6, and 3.$ How much time (in weeks and days) did Eric spend on business trips last year?

Show Solution

5 weeks and 1 day.

30. Renee attached a $6-foot-6-inch$ cord to her computer’s $3-foot-8-inch$ power cord. What was the total length of the cords?

31. Fawzi’s SUV is $6$ feet $4$ inches tall. If he puts a $2-foot-10-inch$ box on top of his SUV, what is the total height of the SUV and the box?

Show Solution

9 ft 2 in .

32. Leilani wants to make $8$ placemats. For each placemat she needs $18$ inches of fabric. How many yards of fabric will she need for the $8$ placemats?

33. Mireille needs to cut $24$ inches of ribbon for each of the $12$ girls in her dance class. How many yards of ribbon will she need altogether?

Show Solution

8 yards.

Make Unit Conversions in the Metric System

In the following exercises, convert the units.

34. Ghalib ran $5$ kilometers. Convert the length to meters.

35. Kitaka hiked $8$ kilometers. Convert the length to meters.

Show Solution

8000 meters.

36. Estrella is $1.55$ meters tall. Convert her height to centimeters.

37. The width of the wading pool is $2.45$ meters. Convert the width to centimeters.

Show Solution

245 centimeters.

38. Mount Whitney is $3,072$ meters tall. Convert the height to kilometers.

39. The depth of the Mariana Trench is $10,911$ meters. Convert the depth to kilometers.

Show Solution

10.911 kilometers.

40. June’s multivitamin contains $1,500$ milligrams of calcium. Convert this to grams.

41. A typical ruby-throated hummingbird weights $3$ grams. Convert this to milligrams.

Show Solution

3000 milligrams.

42. One stick of butter contains $91.6$ grams of fat. Convert this to milligrams.

43. One serving of gourmet ice cream has $25$ grams of fat. Convert this to milligrams.

Show Solution

25,000 milligrams.

44. The maximum mass of an airmail letter is $2$ kilograms. Convert this to grams.

45. Dimitri’s daughter weighed $3.8$ kilograms at birth. Convert this to grams.

Show Solution

3800 grams.

46. A bottle of wine contained $750$ milliliters. Convert this to liters.

47. A bottle of medicine contained $300$ milliliters. Convert this to liters.

Show Solution

0.3 liters.

Use Mixed Units of Measurement in the Metric System

In the following exercises, solve and write your answer in mixed units.

48. Matthias is $1.8$ meters tall. His son is $89$ centimeters tall. How much taller, in centimeters, is Matthias than his son?

49. Stavros is $1.6$ meters tall. His sister is $95$ centimeters tall. How much taller, in centimeters, is Stavros than his sister?

Show Solution

65 centimeters.

50. A typical dove weighs $345$ grams. A typical duck weighs $1.2$ kilograms. What is the difference, in grams, of the weights of a duck and a dove?

51. Concetta had a $2-kilogram$ bag of flour. She used $180$ grams of flour to make biscotti. How many kilograms of flour are left in the bag?

Show Solution

1.82 kilograms .

52. Harry mailed $5$ packages that weighed $420$ grams each. What was the total weight of the packages in kilograms?

53. One glass of orange juice provides $560$ milligrams of potassium. Linda drinks one glass of orange juice every morning. How many grams of potassium does Linda get from her orange juice in $30$ days?

Show Solution

16.8 grams.

54. Jonas drinks $200$ milliliters of water $8$ times a day. How many liters of water does Jonas drink in a day?

55. One serving of whole grain sandwich bread provides $6$ grams of protein. How many milligrams of protein are provided by $7$ servings of whole grain sandwich bread?

Show Solution

42,0000 milligrams.

Convert Between U.S. and Metric Systems

In the following exercises, make the unit conversions. Round to the nearest tenth.

56. Bill is $75$ inches tall. Convert his height to centimeters.

57. Frankie is $42$ inches tall. Convert his height to centimeters.

Show Solution

106.7 centimeters .

58. Marcus passed a football $24$ yards. Convert the pass length to meters.

59. Connie bought $9$ yards of fabric to make drapes. Convert the fabric length to meters.

Show Solution

8.2 meters .

60. Each American throws out an average of $1,650$ pounds of garbage per year. Convert this weight to kilograms (2.20 pounds = 1 kilogram).

61. An average American will throw away $90,000$ pounds of trash over his or her lifetime. Convert this weight to kilograms (2.20 pounds = 1 kilogram).

Show Solution

40,900 kilograms.

62. A $5K$ run is $5$ kilometers long. Convert this length to miles.

63. Kathryn is $1.6$ meters tall. Convert her height to feet.

Show Solution

5.2 feet.

64. Dawn’s suitcase weighed $20$ kilograms. Convert the weight to pounds.

65. Jackson’s backpack weighs $15$ kilograms. Convert the weight to pounds.

Show Solution

33 pounds.

66. Ozzie put $14$ gallons of gas in his truck. Convert the volume to liters.

67. Bernard bought $8$ gallons of paint. Convert the volume to liters.

Show Solution

30.2 liters.

Convert between Fahrenheit and Celsius

In the following exercises, convert the Fahrenheit temperature to degrees Celsius. Round to the nearest tenth.

68. 86°F

69. 77°F

Show Solution

25 °C.

70. 104°F

71. 14°F

Show Solution

-10°C.

72. 72°F

73. 4°F

Show Solution

-15.6°C.

74. 0°F

75. 120°F

Show Solution

48.9°C.

In the following exercises, convert the Celsius temperatures to degrees Fahrenheit. Round to the nearest tenth.

76. 5°C

77. 25°C

Show Solution

77°F.

78. −10°C

79. −15°C

Show Solution

5°F

80. 22°C

81. 8°C

Show Solution

46.4°F.

82. 43°C

83. $16 °C$

Show Solution

60.8°F.

Everyday Math

84. Nutrition Julian drinks one can of soda every day. Each can of soda contains $40$ grams of sugar. How many kilograms of sugar does Julian get from soda in $1$ year?

85. Reflectors The reflectors in each lane-marking stripe on a highway are spaced $16$ yards apart. How many reflectors are needed for a one-mile-long stretch of highway?

Show Solution

110 reflectors.

Writing Exercises

86. Some people think that $65 °$ to $75 °$ Fahrenheit is the ideal temperature range.

ⓐ What is your ideal temperature range? Why do you think so?
ⓑ Convert your ideal temperatures from Fahrenheit to Celsius.

87. ⓐ Did you grow up using the U.S. customary or the metric system of measurement? ⓑ Describe two examples in your life when you had to convert between systems of measurement. ⓒ Which system do you think is easier to use? Explain.

Units and Conversion Factors

1. Is one liter about an ounce, a pint, a quart, or a gallon?

Solution

A liter is approximately equal to a quart.

2. Is a meter about an inch, a foot, a yard, or a mile?

3. Write conversion factors (as ratios) for the number of:

(a) yards in 1 meter

(b) liters in 1 liquid quart

(c) pounds in 1 kilogram

Solution

(a) [latex]\frac{1.0936\text{ yd}}{1\text{ m}}[/latex], (b) [latex]\frac{1\text{ L}}{1.0567\text{ qt}}[/latex], (c) [latex]\frac{2.2046\text{ lb}}{1\text{ kg}}[/latex]

4. Write conversion factors (as ratios) for the number of:

(a) kilometers in 1 mile

(b) liters in 1 cubic foot

(c) grams in 1 ounce

5. The label on a soft drink bottle gives the volume in two units: 2 L and 67.6 fl oz. Use this information to derive a conversion factor between the English and metric units.

Solution

[latex]\frac{2\text{ L}}{67.6\text{ fl.oz.}}\text{ or }\frac{67.6\text{ fl.oz.}}{2\text{ L}}[/latex]

6. The label on a box of cereal gives the mass of cereal in two units: 978 grams and 34.5 oz. Use this information to find a conversion factor between the English and metric units.

The Metric System

7. Many medical laboratory tests are run using 5.0 microliter blood serum. What is this volume in milliliters if there are 1 million microliters in one liter?

Solution

0.005 mL

8. If an aspirin tablet contains 325 mg aspirin, how many grams of aspirin does it contain?

9. 612 g = ________ mg

Solution

612,000 mg

10. 8.160 m = ________ cm

11. 3779 mg = ________ g

Solution

3.779 g

12. 781 mL = ________ L

13. 4.18 kg = ________ g

Solution

4180 g

14. 27.8 m = ________ km

15. 0.13 mL = ________ L

Solution

0.00013 L

16. 1738 km = ________ m

17. 1.9 g = ________ kg

Solution

0.0019 kg

Converting Between Units

18. Soccer is played with a round ball having a circumference between 27 and 28 in. and a weight between 14 and 16 oz. What are these specifications in units of centimeters and grams?

19. A women’s basketball has a circumference between 28.5 and 29.0 inches and a maximum weight of 20 ounces. What are these specifications in units of centimeters and grams?

Solution

The circumference is between 72.4 and 73.7 centimeters, and the weight is between 397 and 454 grams.

20. How many milliliters of a soft drink are contained in a 12.0-oz can?

21. A barrel of oil is exactly 42 gal. How many liters of oil are in a barrel?

Solution

159 L

22. The diameter of a red blood cell is about 0.0003 in. What is its diameter in centimeters?

23. Is a 197-lb weight lifter light enough to compete in a class limited to those weighing 90 kg or less?

Solution

No, the weight lifter is about 198.4 lbs.

24. A very good weight lifter lifted 192 kg in a move called the clean and jerk. What was the mass of the weight lifted in pounds?

25. Gasoline is sold by the liter in many countries. How many liters are required to fill a 12.0-gal gas tank?

Solution

45.4 L

26. Milk is sold by the liter in many countries. What is the volume of a half-gallon of milk in liters?

27. A long ton is defined as exactly 2240 lb. What is this mass in kilograms?

Solution

1016 kg

28. Make the conversion indicated in each of the following:

(a) the men’s world record long jump, 29 ft 4¼ in., to meters

(b) the greatest depth of the ocean, about 6.5 mi, to kilometers

(c) the volume of 1 gill (exactly 4 oz) to milliliters

(d) the mass of a 3525-lb car to kilograms

(e) the mass of a 2.3-oz egg to grams

29. Make the conversion indicated in each of the following:

(a) the length of a soccer field, 120 m, to feet

(b) the height of Mt. Kilimanjaro, at 19,565 ft, the highest mountain in Africa, to kilometers

(c) the mass of a pencil, 0.0085 kg, to ounces

(d) the mass of a bushel of rye, 32.0 lb, to kilograms

(e) the mass of a 5.00-grain aspirin tablet to milligrams (1 grain = 0.00229 oz)

Solution

(a) 394 ft, (b) 5.96 km, (c) 0.3 oz, (d) 14.5 kg, (e) 0.01145 oz

30. Soccer fields vary in size. A large soccer field is 115 m long and 85 m wide. What are its dimensions in feet and inches? (Assume that 1 meter equals 3.281 feet.)

31. What is the height in meters of a person who is 6 ft 1 in. tall? (Assume that 1 meter equals 39.37 in.)

Solution

1.85 m

32. Mount Everest, at 29,028 feet, is the tallest mountain on the Earth. What is its height in kilometers? (Assume that 1 kilometer equals 3,281 feet.)

33. To prepare for a laboratory period, a student lab assistant needs 125 g of a compound. A bottle containing 1/4 lb is available. Did the student have enough of the compound?

Solution

No, the bottle contains only 113.4 g of the compound.

34. An algebra student is 159 cm tall and weighs 45.8 kg. What is her height in inches and weight in pounds?

Converting Area and Volume

35. the area of the state of Oregon, 96,981 mi², to square kilometers

Solution

About 251, 170 km²

36. the estimated volume of the oceans, 330,000,000 mi³, to cubic kilometers.

37. the area of an 8.5- × 11-inch sheet of paper in cm²

Solution

603 cm²

38. the displacement volume of an automobile engine, 161 in.³, to liters

Rate Conversions

39. In a recent Grand Prix, the winner completed the race with an average speed of 229.8 km/h. What was his speed in miles per hour, meters per second, and feet per second?

Solution

142.8 mph, 63.8 m/s, 209.4 ft/s

40. A car is traveling at a speed of 33 m/s. (a) What is its speed in kilometers per hour? (b) Is it exceeding the 90 km/h speed limit?

41. If a marathon runner averages 9.5 mi/h, how long does it take him or her to run a 26.22-mi marathon?

Solution

2 hours and 55 minutes

42. A marathon runner completes a 42.188 km course in 2 hours, 30 minutes, and 12 seconds. What is her average speed in meters per second?

43. The speed of sound is measured to be 342 m/s on a certain day. What is this in km/h?

Solution

1231 km/h

44. Tectonic plates are large segments of the Earth’s crust that move slowly. Suppose that one such plate has an average speed of 4.0 cm/year. (a) What distance does it move in 1 s at this speed? (b) What is its speed in kilometers per million years?

45. Amanda wants to take a 513 mile trip to see a friend. According to her car’s owner’s manual, the gas tank 22.3 gallons and the fuel efficiency is 38 miles per gallon.

(a) How many tanks of gas will Amanda use on her trip?

(b) If gasoline costs $2.87 per gallon, how much will she spend on gas?

Solution

(a) 0.605 tanks, (b) $38.75

Glossary

conversion factor

A conversion factor (or unit conversion factor) is a ratio of two equivalent quantities expressed with different measurement units.

metric system

The metric system is a decimal system of measurement which is based on a fundamental set of units including the meter, the second, and the kilogram.

rate

A rate is a quantity which is computed from measurements in two or more different units.

rate conversion

Rate conversions are unit conversions involving several different quantities.

unit

Units are standardized values used to express measurements of physical quantities.

unit equivalence

A unit equivalence tells you how many of one unit are equivalent to exactly one of another unit.

Media Attributions

License

Icon for the Creative Commons Attribution 4.0 International License

0.3 Unit Conversions Copyright © by Karen Perilloux; Prakash Ghimire; Kristina VanDusen; and Lauren Johnson is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.