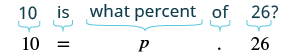0.6 Percentages
Karen Perilloux; Prakash Ghimire; Kristina VanDusen; and Lauren Johnson
Learning Objectives
By the end of this section, you will be able to:
- Use the definition of percent
- Convert percents to fractions and decimals
- Convert decimals and fractions to percents
- Translate and solve basic percent equations
- Solve applications of percent
- Find percent increase and percent decrease
Use the Definition of Percent
How many cents are in one dollar? There are 100 cents in a dollar.
How many years are in a century? There are 100 years in a century.
Does this give you a clue about what the word “percent” means? It is really two words, “per cent,” and means per one hundred. A percent is a ratio whose denominator is 100.
We use the percent symbol, %, to show percent.
Percent
A percent is a ratio whose denominator is 100.
According to data from the American Association of Community Colleges (2015), about 57% of community college students are female. This means 57 out of every 100 community college students are female, as Figure 1 shows. Out of the 100 squares on the grid, 57 are shaded, which we write as the ratio [latex]\frac{57}{100}[/latex].

Similarly, [latex]25%[/latex] means a ratio of [latex]\frac{25}{100}[/latex], [latex]3%[/latex] means a ratio of [latex]\frac{3}{100}[/latex], and [latex]100%[/latex] means a ratio of [latex]\frac{100}{100}[/latex].
In words, “one hundred percent” means the total [latex]100%[/latex] is [latex]\frac{100}{100}[/latex], and since [latex]\frac{100}{100}=1[/latex], we see that [latex]100%[/latex] means 1 whole.
Example
According to the Public Policy Institute of California (2010), 44% of parents of public school children would like their youngest child to earn a graduate degree. Write this percent as a ratio.
Solution
| The amount we want to convert is 44%. | |
| Write the percent as a ratio. Remember that percent means per 100. |
Try It
Write the percent as a ratio.
According to a survey, 89% of college students have a smartphone.
Show Solution
[latex]\frac{89}{100}[/latex]
Try It
Write the percent as a ratio.
A study found that 72% of U.S. teens send text messages regularly.
Show Solution
[latex]\frac{72}{100}[/latex]
Example
In 2007, according to a U.S. Department of Education report, 21 out of every 100 first-time freshmen college students at 4-year public institutions took at least one remedial course. Write this as a ratio and then as a percent.
Solution
| The amount we want to convert is 21 out of 100. | [latex]21 \text{ out of }100[/latex] |
| Write as a ratio. | |
| Convert the 21 per 100 to percent. |
Try It
Write as a ratio and then as a percent: The American Association of Community Colleges reported that 62 out of 100 full-time community college students balance their studies with full-time or part time employment.
Show Solution
[latex]\frac{62}{100}\text{ or }62\%[/latex]
Try It
Write as a ratio and then as a percent: In response to a student survey, 41 out of 100 Santa Ana College students expressed a goal of earning an Associate’s degree or transferring to a four-year college.
Show Solution
[latex]\frac{41}{100}\text{ or }41\%[/latex]
Convert Percents to Fractions and Decimals
Since percents are ratios, they can easily be expressed as fractions. Remember that percent means per 100, so the denominator of the fraction is 100.
How To
Convert a percent to a fraction.
- Write the percent as a ratio with the denominator 100.
- Simplify the fraction if possible.
Example
Convert each percent to a fraction:
a) [latex]36\%[/latex]
b) [latex]125\%[/latex]
Solution to part (a)
| Write as a ratio with denominator 100. | |
| Simplify. |
Solution to part (b)
| Write as a ratio with denominator 100. | |
| Simplify. |
Try It
Convert each percent to a fraction:
a) [latex]48\%[/latex]
b) [latex]110\%[/latex]
Show Solution
Try It
Convert each percent to a fraction:
a) [latex]64\%[/latex]
b) [latex]150\%[/latex]
Show Solution
The previous example shows that a percent can be greater than 1. We saw that [latex]125\%[/latex] means [latex]\frac{125}{100}[/latex], or [latex]\frac{5}{4}[/latex]. These are improper fractions, and their values are greater than one.
Example
Convert each percent to a fraction:
a) [latex]24.5\%[/latex]
b) [latex]33\frac{1}{3}\%[/latex]
Solution to part (a)
| Write as a ratio with denominator 100. | |
| Clear the decimal by multiplying numerator and denominator by 10. | |
| Multiply. | |
| Rewrite showing common factors. | |
| Simplify. |
Solution to part (b)
| Write as a ratio with denominator 100. | |
| Write the numerator as an improper fraction. | |
| Rewrite as fraction division, replacing 100 with [latex]\frac{100}{1}[/latex]. | |
| Multiply by the reciprocal. | |
| Simplify. |
Try It
Convert each percent to a fraction:
a) [latex]64.4\%[/latex]
b) [latex]66\frac{2}{3}\%[/latex]
Show Solution
Try It
Convert each percent to a fraction:
a) [latex]42.5\%[/latex]
b) [latex]8\frac{3}{4}\%[/latex]
Show Solution
How To
Convert a percent to a decimal.
- Write the percent as a ratio with the denominator 100.
- Convert the fraction to a decimal by dividing the numerator by the denominator.
Example
Convert each percent to a decimal:
a) [latex]6\%[/latex]
b) [latex]78\%[/latex]
Solution to part (a)
Because we want to change to a decimal, we will leave the fractions with denominator 100 instead of removing common factors.
| Write as a ratio with denominator 100. | |
| Change the fraction to a decimal by dividing the numerator by the denominator. |
Solution to part (b)
| Write as a ratio with denominator 100. | |
| Change the fraction to a decimal by dividing the numerator by the denominator. |
Try It
Convert each percent to a decimal:
a) [latex]9\%[/latex]
b) [latex]87\%[/latex]
Show Solution
Try It
Convert each percent to a decimal:
a) [latex]3\%[/latex]
b) [latex]91\%[/latex]
Show Solution
Example
Convert each percent to a decimal:
a) [latex]135\%[/latex]
b) [latex]12.5\%[/latex]
Solution to part (a)
| Write as a ratio with denominator 100. | |
| Change the fraction to a decimal by dividing the numerator by the denominator. |
Solution to part (b)
| Write as a ratio with denominator 100. | |
| Change the fraction to a decimal by dividing the numerator by the denominator. |
Try It
Convert each percent to a decimal:
a) [latex]115\%[/latex]
b) [latex]23.5\%[/latex]
Show Solution
Try It
Convert each percent to a decimal:
a) [latex]123\%[/latex]
b) [latex]16.8\%[/latex]
Show Solution
| Percent | Decimal |
|---|---|
To convert a percent number to a decimal number, we move the decimal point two places to the left and remove the % sign. (Sometimes the decimal point does not appear in the percent number, but just like we can think of the integer 6 as 6.0, we can think of 6% as 6.0%.) Notice that we may need to add zeros in front of the number when moving the decimal to the left.

Example
Among a group of business leaders, 77% believe that poor math and science education in the U.S. will lead to higher unemployment rates.
Convert the percent to: (a) a fraction (b) a decimal.
Solution to part (a)
| Write as a ratio with denominator 100. |
Solution to part (b)
| Change the fraction to a decimal by dividing the numerator by the denominator. |
Try It
Convert the percent to: (a) a fraction and (b) a decimal.
Twitter’s share of web traffic jumped 24% when one celebrity tweeted live on air.
Show Solution
Try It
Convert the percent to: (a) a fraction and (b) a decimal.
The U.S. Census estimated that in 2013, 44% of the population of Boston age 25 or older have a bachelor’s or higher degrees.
Show Solution
Example
There are four suits of cards in a deck of cards—hearts, diamonds, clubs, and spades. The probability of randomly choosing a heart from a shuffled deck of cards is 25%.
Convert the percent to: (a) a fraction and (b) a decimal.

Solution to part (a)
| Write as a ratio with denominator 100. | |
| Simplify. |
Solution to part (b)
| Change the fraction to a decimal by dividing the numerator by the denominator. |
Try It
Convert the percent to: (a) a fraction, and (b) a decimal.
The probability that it will rain Monday is 30%.
Show Solution
Try It
Convert the percent to: (a) a fraction, and (b) a decimal.
The probability of getting heads three times when tossing a coin three times is 12.5%.
Show Solution
Convert Decimals and Fractions to Percents
To convert a decimal to a percent, remember that percent means per hundred. If we change the decimal to a fraction whose denominator is 100, it is easy to change that fraction to a percent.
How To
Convert a decimal to a percent.
- Write the decimal as a fraction.
- If the denominator of the fraction is not 100, rewrite it as an equivalent fraction with denominator 100.
- Write this ratio as a percent.
Example
Convert each decimal to a percent:
a) [latex]0.05[/latex]
b) [latex]0.83[/latex]
Solution to part (a)
| Write as a fraction. The denominator is 100. | |
| Write this ratio as a percent. |
Solution to part (b)
| The denominator is 100. | |
| Write this ratio as a percent. |
Try It
Convert each decimal to a percent:
a) [latex]0.01[/latex]
b) [latex]0.17[/latex]
Show Solution
Try It
Convert each decimal to a percent:
a) [latex]0.04[/latex]
b) [latex]0.41[/latex]
Show Solution
To convert a mixed number to a percent, we first write it as an improper fraction.
Example
Convert each decimal to a percent:
a) [latex]1.05[/latex]
b) [latex]0.075[/latex]
Solution to part (a)
| Write as a fraction. | |
| Write as an improper fraction. The denominator is 100. | |
| Write this ratio as a percent. |
Notice that since [latex]1.05>1[/latex], the result is more than [latex]100\%[/latex].
Solution to part (b)
| Write as a fraction. The denominator is 1,000. | |
| Divide the numerator and denominator by 10, so that the denominator is 100. | |
| Write this ratio as a percent. |
Try It
Convert each decimal to a percent:
a) [latex]1.75[/latex]
b) [latex]0.0825[/latex]
Show Solution
Try It
Convert each decimal to a percent:
a) [latex]2.25[/latex]
b) [latex]0.0925[/latex]
Show Solution
Let’s summarize the results from the previous examples in Table 2 so we can look for a pattern.
| Decimal | Percent |
|---|---|
Do you see the pattern? To convert a decimal to a percent, we move the decimal point two places to the right and then add the percent sign.
We have learned how to convert fractions to decimals. Now we also know how to change decimals to percents. So to convert a fraction to a percent, we first change it to a decimal and then convert that decimal to a percent.
How To
Convert a fraction to a percent.
- Convert the fraction to a decimal.
- Convert the decimal to a percent.
Example
Convert each fraction or mixed number to a percent:
a) [latex]\frac{3}{4}[/latex]
b) [latex]\frac{11}{8}[/latex]
c) [latex]2\frac{1}{5}[/latex]
Solution to part (a)
To convert a fraction to a decimal, divide the numerator by the denominator.
| Change to a decimal. | |
| Write as a percent by moving the decimal two places. | |
Solution to part (b)
| Change to a decimal. | |
| Write as a percent by moving the decimal two places. | |
Solution to part (c)
| Write as an improper fraction. | |
| Change to a decimal. | |
| Write as a percent. | |
Notice that we needed to add zeros at the end of the number when moving the decimal two places to the right.
Try It
Convert each fraction or mixed number to a percent:
a) [latex]\frac{5}{8}[/latex]
b) [latex]\frac{11}{4}[/latex]
c) [latex]3\frac{2}{5}[/latex]
Show Solution
Try It
Convert each fraction or mixed number to a percent:
a) [latex]\frac{7}{8}[/latex]
b) [latex]\frac{9}{4}[/latex]
c) [latex]1\frac{3}{5}[/latex]
Show Solution
Sometimes when changing a fraction to a decimal, the division continues for many decimal places and we will round off the quotient. The number of decimal places we round to will depend on the situation. If the decimal involves money, we round to the hundredths place. For most other cases in this book we will round the number to the nearest thousandth, so the percent will be rounded to the nearest tenth.
Example
Convert [latex]\frac{5}{7}[/latex] to a percent.
Solution
To change a fraction to a decimal, we divide the numerator by the denominator.
| Change to a decimal—rounding to the nearest thousandth. | |
| Write as a percent. |
Try It
Convert the fraction to a percent: [latex]\frac{3}{7}[/latex].
Show Solution
[latex]42.9\%[/latex]
Try It
Convert the fraction to a percent: [latex]\frac{4}{7}[/latex].
Show Solution
[latex]57.1\%[/latex]
When we first looked at fractions and decimals, we saw that some fractions converted to a repeating decimal. For example, when we converted the fraction [latex]\frac{4}{3}[/latex] to a decimal, we wrote the answer as [latex]1.\bar{3}[/latex].
We will use this same notation, as well as fraction notation, when we convert fractions to percents in the next example.
Example
An article in a medical journal claimed that approximately [latex]\frac{1}{3}[/latex] of American adults are obese. Convert the fraction [latex]\frac{1}{3}[/latex] to a percent.
Solution
| Change to a decimal. | 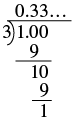 |
| Write as a repeating decimal. | |
| Write as a percent. |
We could also write the percent as [latex]33.\bar{3}\%[/latex].
Try It
Convert the fraction to a percent:
According to the U.S. Census Bureau, about [latex]\frac{1}{9}[/latex] of United States housing units have just 1 bedroom.
Show Solution
[latex]11.\bar{1}\%[/latex]
Try It
Convert the fraction to a percent:
According to the U.S. Census Bureau, about [latex]\frac{1}{6}[/latex] of Colorado residents speak a language other than English at home.
Show Solution
[latex]16.\bar{6}\%[/latex]
Translate and Solve Basic Percent Equations
We will solve percent equations by using the methods we used to solve equations with fractions or decimals. In the past, you may have solved percent problems by setting them up as proportions. That was the best method available when you did not have the tools of algebra. Now as a prealgebra student, you can translate word sentences into algebraic equations, and then solve the equations.
We’ll look at a common application of percent—tips to a server at a restaurant—to see how to set up a basic percent application.
When Aolani and her friends ate dinner at a restaurant, the bill came to $80. They wanted to leave a 20% tip. What amount would the tip be?
To solve this, we want to find what amount is 20% of $80. The $80 is called the base. The amount of the tip would be 0.20(80), or $16. See Figure 4. To find the amount of the tip, we multiplied the percent by the base.

In the next examples, we will find the amount. We must be sure to change the given percent to a decimal when we translate the words into an equation.
Example
What number is 35% of 90?
Solution
Solution
| Translate into algebra. Let n equal the number. | 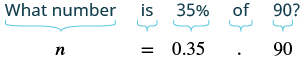 |
| Multiply. | |
| 31.5 is 35% of 90. |
Try It
What number is 45% of 80?
Show Solution
36
Try It
What number is 55% of 60?
Show Solution
33
Example
125% of 28 is what number?
Solution
Solution
| Translate into algebra. Let ‘a’ equal the number. |
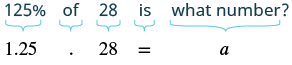 |
| Multiply. | |
|
|
Remember that a percent over 100 is a number greater than 1. We found that 125% of 28 is 35, which is greater than 28.
Try It
150% of 78 is what number?
Show Solution
117
Try It
175% of 72 is what number?
Show Solution
126
Example
Translate and solve: 36 is 75% of what number?
Solution
Solution
| Translate. Let b = the number. | 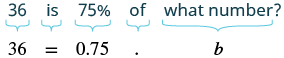 |
| Divide both sides by 0.75. | |
| Simplify. |
Try It
17 is 25% of what number?
Show Solution
68
Try It
40 is 62.5% of what number?
Show Solution
64
Example
6.5% of what number is $1.17?
Solution
Solution
| Translate. Let b = the number. | 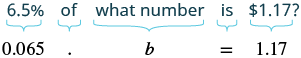 |
| Divide both sides by 0.065. | |
| Simplify. |
Try It
7.5% of what number is $1.95?
Show Solution
$26
Try It
8.5% of what number is $3.06?
Show Solution
$36
In the next examples, we will solve for the percent.
Example
What percent of 36 is 9?
Solution
Solution
| Translate into algebra. Let p = the percent. |  |
| Divide by 36. | |
| Simplify. | |
| Convert to decimal form. | |
| Convert to percent. |
Try It
What percent of 76 is 57?
Show Solution
75%
Try It
What percent of 120 is 96?
Show Solution
80%
Example
Solution
Solution
| Translate into algebra.
Let p = the percent. |
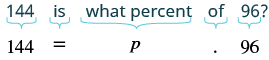 |
|
Divide by 96. |
|
|
Simplify. |
|
|
Convert to percent. |
|
Try It
110 is what percent of 88?
Show Solution
125%
Try It
126 is what percent of 72?
Show Solution
175%
Solve Applications of Percent
Many applications of percent occur in our daily lives, such as tips, sales tax, discount, and interest. To solve these applications we’ll translate to a basic percent equation, just like those we solved in the previous examples in this section. Once you translate the sentence into a percent equation, you know how to solve it.
We will update the strategy we used in our earlier applications to include equations now. Notice that we will translate a sentence into an equation.
How to
Solve an application
Step 1. Identify what you are asked to find and choose a variable to represent it.
Step 2. Write a sentence that gives the information to find it.
Step 3. Translate the sentence into an equation.
Step 4. Solve the equation using good algebra techniques.
Step 5. Check the answer in the problem and make sure it makes sense.
Step 6. Write a complete sentence that answers the question.
Now that we have the strategy to refer to, and have practiced solving basic percent equations, we are ready to solve percent applications. Be sure to ask yourself if your final answer makes sense—since many of the applications we’ll solve involve everyday situations, you can rely on your own experience.
Example
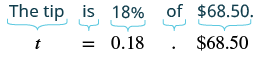
Dezohn and his girlfriend enjoyed a dinner at a restaurant, and the bill was $68.50. They want to leave an 18% tip. If the tip will be 18% of the total bill, how much should the tip be?
Solution
| What are you asked to find? | the amount of the tip |
| Choose a variable to represent it. | Let t = amount of tip. |
| Write a sentence that give the information to find it. | The tip is 18% of the total bill. |
| Translate the sentence into an equation. |
|
| Multiply. | |
|
Check. Is this answer reasonable? |
|
|
If we approximate the bill to $70 and the percent to 20%, we would have a tip of $14. So a tip of $12.33 seems reasonable. |
|
|
Write a complete sentence that answers the question. |
The couple should leave a tip of $12.33. |
Try It
Cierra and her sister enjoyed a special dinner in a restaurant, and the bill was $81.50. If she wants to leave 18% of the total bill as her tip, how much should she leave?
Show Solution
$14.67
Try It
Kimngoc had lunch at her favorite restaurant. She wants to leave 15% of the total bill as her tip. If her bill was $14.40, how much will she leave for the tip?
Show Solution
$2.16
Example
The label on Masao’s breakfast cereal said that one serving of cereal provides 85 milligrams (mg) of potassium, which is 2% of the recommended daily amount. What is the total recommended daily amount of potassium?

Solution
|
What are you asked to find? |
the total amount of potassium recommended |
|
Choose a variable to represent it. |
Let a = total amount of potassium. |
|
Write a sentence that gives the information to find it. |
85 mg is 2% of the total amount. |
|
Translate the sentence into an equation. |
 |
|
Divide both sides by 0.02. |
|
|
Simplify. |
|
|
Check: Is this answer reasonable? |
|
|
Yes. 2% is a small percent and 85 is a small part of 4,250. |
|
|
Write a complete sentence that answers the question. |
The amount of potassium that is recommended is 4250 mg. |
Try It
One serving of wheat square cereal has 7 grams of fiber, which is 29% of the recommended daily amount. What is the total recommended daily amount of fiber?
Show Solution
24.1 grams
Try It
One serving of rice cereal has 190 mg of sodium, which is 8% of the recommended daily amount. What is the total recommended daily amount of sodium?
Show Solution
2,375 mg
Example
Mitzi received some gourmet brownies as a gift. The wrapper said each brownie was 480 calories, and had 240
calories of fat. What percent of the total calories in each brownie comes from fat?
Solution
| What are you asked to find? | the percent of the total calories from fat |
|
Choose a variable to represent it. |
Let p = percent from fat. |
|
Write a sentence that gives the information to find it. |
What percent of 480 is 240? |
|
Translate the sentence into an equation. |
|
|
Divide both sides by 480. |
|
|
Simplify. |
|
|
Convert to percent form. |
|
|
Check. Is this answer reasonable? |
|
|
Yes. 240 is half of 480, so 50% makes sense. |
|
|
Write a complete sentence that answers the question. |
Of the total calories in each brownie, 50% is fat. |
Try It
Veronica is planning to make muffins from a mix. The package says each muffin will be 230 calories and 60 calories will be from fat. What percent of the total calories is from fat? (Round to the nearest whole percent.)
Show Solution
26%
Try It
The brownie mix Ricardo plans to use says that each brownie will be 190 calories, and 70 calories are from fat. What percent of the total calories are from fat?
Show Solution
37%
Find Percent Increase and Percent Decrease
People in the media often talk about how much an amount has increased or decreased over a certain period of time. They usually express this increase or decrease as a percent.
To find the percent increase, first we find the amount of increase, which is the difference between the new amount and the original amount. Then we find what percent the amount of increase is of the original amount.
How To
Find Percent Increase
Step 1. Find the amount of increase.
Step 2. Find the percent increase as a percent of the original amount.
Example
In 2011, the California governor proposed raising community college fees from $26 per unit to $36 per unit. Find the percent increase. (Round to the nearest tenth of a percent.)
Solution
| What are you asked to find? | the percent increase |
|
Choose a variable to represent it. |
Let p = percent. |
| Find the amount of increase. |
|
| Find the percent increase. |
The increase is what percent of the original amount? |
|
Translate to an equation. |
|
|
Divide both sides by 26. |
|
|
Round to the nearest thousandth. |
|
|
Convert to percent form. |
|
|
Write a complete sentence. |
The new fees represent a 38.5% increase over the old fees. |
Try it
In 2011, the IRS increased the deductible mileage cost to 55.5 cents from 51 cents. Find the percent increase. (Round to the nearest tenth of a percent.)
Show Solution
8.8%
Try it
In 1995, the standard bus fare in Chicago was $1.50. In 2008, the standard bus fare was $2.25. Find the percent increase. (Round to the nearest tenth of a percent.)
Show Solution
50%
Finding the percent decrease is very similar to finding the percent increase, but now the amount of decrease is the difference between the original amount and the final amount. Then we find what percent the amount of decrease is of the original amount.
How to
Find Percent Decrease
Step 1. Find the amount of decrease.
Step 2. Find the percent decrease as a percent of the original amount.
Example
The average price of a gallon of gas in one city in June 2014 was $3.71. The average price in that city in July was $3.64. Find the percent decrease.
Solution
| What are you asked to find? | the percent decrease |
|
Choose a variable to represent it. |
Let p =percent. |
|
Find the amount of decrease. |
|
| Find the percent of decrease. | The decrease is what percent of the original amount? |
| Translate to an equation. | 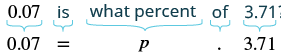 |
| Divide both sides by 3.71. | |
| Round to the nearest thousandth. | |
| Convert to percent form. | |
|
Write a complete sentence. |
The price of gas decreased 1.9%. |
Try it
The population of one city was about 672,000 in 2010. The population of the city is projected to be about 630,000 in 2020. Find the percent decrease. (Round to the nearest tenth of a percent.)
Show Solution
6.3%
Try it
Last year Sheila’s salary was $42,000. Because of furlough days, this year her salary was $37,800. Find the percent decrease. (Round to the nearest tenth of a percent.)
Show Solution
10%
Media
ACCESS ADDITIONAL ONLINE RESOURCES
Key Concepts
Convert a percent to a fraction.
-
- Step 1. Write the percent as a ratio with the denominator 100.
- Step 2. Simplify the fraction if possible.
Convert a percent to a decimal.
-
- Step 1. Write the percent as a ratio with the denominator 100.
- Step 2. Convert the fraction to a decimal by dividing the numerator by the denominator.
Convert a decimal to a percent.
-
- Step 1. Write the decimal as a fraction.
- Step 2. If the denominator of the fraction is not 100, rewrite it as an equivalent fraction with denominator 100.
- Step 3. Write this ratio as a percent.
Convert a fraction to a percent.
-
- Step 1. Convert the fraction to a decimal.
- Step 2. Convert the decimal to a percent.
Solve an application.
Step 1. Identify what you are asked to find and choose a variable to represent it.
Step 2. Write a sentence that gives the information to find it.
Step 3. Translate the sentence into an equation.
Step 4. Solve the equation using good algebra techniques.
Step 5. Write a complete sentence that answers the question.
Step 6. Check the answer in the problem and make sure it makes sense.
Find percent decrease.
Step 1. Find the amount of decrease.
-
-
- decrease = original amount – new amount
-
Step 2 .Find the percent increase as a percent of the original amount.
Section Exercises
Use the Definition of Percents
In the following exercises, write each percent as a ratio.
1. In 2014, the unemployment rate for those with only a high school degree was 6.0%.
Solution
2. In 2015, among the unemployed, 29% were long-term unemployed.
3. The unemployment rate for those with Bachelor’s degrees was 3.2% in 2014.
Solution
4. The unemployment rate in Michigan in 2014 was 7.3%.
In the following exercises, write as (a) a ratio and (b) a percent.
5. 57 out of 100 nursing candidates received their degree at a community college.
Solution
6. 80 out of 100 firefighters and law enforcement officers were educated at a community college.
7. 42 out of 100 first-time freshmen students attend a community college.
Solution
8. 71 out of 100 full-time community college faculty have a master’s degree.
Convert Percents to Fractions and Decimals
In the following exercises, convert each percent to a fraction and simplify all fractions.
9. [latex]4\%[/latex]
Solution
10. [latex]8\%[/latex]
11. [latex]17\%[/latex]
Solution
12. [latex]19\%[/latex]
13. [latex]52\%[/latex]
Solution
14. [latex]78\%[/latex]
15. [latex]125\%[/latex]
Solution
16. [latex]135\%[/latex]
17. [latex]37.5\%[/latex]
Solution
18. [latex]42.5\%[/latex]
19. [latex]18.4\%[/latex]
Solution
20. [latex]46.4\%[/latex]
21. [latex]9\frac{1}{2}\%[/latex]
Solution
22. [latex]8\frac{1}{2}\%[/latex]
23. [latex]5\frac{1}{3}\%[/latex]
Solution
24. [latex]6\frac{2}{3}\%[/latex]
In the following exercises, convert each percent to a decimal.
25. [latex]5\%[/latex]
Solution
26. [latex]9\%[/latex]
27. [latex]1\%[/latex]
Solution
28. [latex]2\%[/latex]
29. [latex]63\%[/latex]
Solution
30. [latex]71\%[/latex]
31. [latex]40\%[/latex]
Solution
32. [latex]50\%[/latex]
33. [latex]115\%[/latex]
Solution
34. [latex]125\%[/latex]
35. [latex]150\%[/latex]
Solution
36. [latex]250\%[/latex]
37. [latex]21.4\%[/latex]
Solution
38. [latex]39.3\%[/latex]
39. [latex]7.8\%[/latex]
Solution
40. [latex]6.4\%[/latex]
In the following exercises, convert each percent to (a) a simplified fraction and (b) a decimal.
41. In 2010, 1.5% of home sales had owner financing. (Source: Bloomberg Businessweek, 5/23–29/2011)
Solution
42. In 2000, 4.2% of the United States population was of Asian descent. (Source: www.census.gov)
43. According to government data, in 2013 the number of cell phones in India was 70.23% of the population.
Solution
44. According to the U.S. Census Bureau, among Americans age 25 or older who had doctorate degrees in 2014, 37.1% are women.
45. A couple plans to have two children. The probability they will have two girls is 25%.
Solution
46. Javier will choose one digit at random from 0 through 9. The probability he will choose 3 is 10%.
47. According to the local weather report, the probability of thunderstorms in New York City on July 15 is 60%.
Solution
48. A club sells 50 tickets to a raffle. Osbaldo bought one ticket. The probability he will win the raffle is 2%.
Convert Decimals and Fractions to Percents
In the following exercises, convert each decimal to a percent.
49. [latex]0.01[/latex]
Solution
50. [latex]0.03[/latex]
51. [latex]0.18[/latex]
Solution
52. [latex]0.15[/latex]
53. [latex]1.35[/latex]
Solution
54. [latex]1.56[/latex]
55. [latex]3[/latex]
Solution
56. [latex]4[/latex]
57. [latex]0.009[/latex]
Solution
58. [latex]0.008[/latex]
59. [latex]0.0875[/latex]
Solution
60. [latex]0.0625[/latex]
61. [latex]1.5[/latex]
Solution
62. [latex]2.2[/latex]
63. [latex]2.254[/latex]
Solution
64. [latex]2.317[/latex]
In the following exercises, convert each fraction to a percent.
65. [latex]\frac{1}{4}[/latex]
Solution
66. [latex]\frac{1}{5}[/latex]
67. [latex]\frac{3}{8}[/latex]
Solution
68. [latex]\frac{5}{8}[/latex]
69. [latex]\frac{7}{4}[/latex]
Solution
70. [latex]\frac{9}{8}[/latex]
71. [latex]6\frac{4}{5}[/latex]
Solution
72. [latex]5\frac{1}{4}[/latex]
73. [latex]\frac{5}{12}[/latex]
Solution
74. [latex]\frac{11}{12}[/latex]
75. [latex]2\frac{2}{3}[/latex]
Solution
76. [latex]1\frac{2}{3}[/latex]
77. [latex]\frac{3}{7}[/latex]
Solution
78. [latex]\frac{6}{7}[/latex]
79. [latex]\frac{5}{9}[/latex]
Solution
80. [latex]\frac{4}{9}[/latex]
In the following exercises, convert each fraction to a percent.
81. [latex]\frac{1}{4}[/latex] of washing machines needed repair.
Solution
82. [latex]\frac{1}{5}[/latex]of dishwashers needed repair.
83. According to the National Center for Health Statistics, in 2012, [latex]\frac{7}{20}[/latex] of American adults were obese.
Solution
84. The U.S. Census Bureau estimated that in 2013, 85% of Americans lived in the same house as they did 1 year before.
In the following exercises, complete the table.
85.
| Fraction | Decimal | Percent |
|---|---|---|
Solution
| Fraction | Decimal | Percent |
|---|---|---|
| [latex]\frac{1}{2}[/latex] | [latex]0.5[/latex] | [latex]50\%[/latex] |
| [latex]\frac{9}{20}[/latex] | [latex]0.45[/latex] | [latex]45\%[/latex] |
| [latex]\frac{9}{50}[/latex] | [latex]0.18[/latex] | [latex]18\%[/latex] |
| [latex]\frac{1}{3}[/latex] | [latex]0.\bar{3}[/latex] | [latex]33.\bar{3}\%[/latex] |
| [latex]\frac{1}{125}[/latex] | [latex]0.008[/latex] | [latex]0.8\%[/latex] |
| [latex]2[/latex] | [latex]2[/latex] | [latex]200\%[/latex] |
| Fraction | Decimal | Percent |
|---|---|---|
Everyday Math
87. Sales tax Felipa says she has an easy way to estimate the sales tax when she makes a purchase. The sales tax in her city is 9.05%. She knows this is a little less than 10%.
a) Convert 10% to a fraction.
b) Use your answer from (a) to estimate the sales tax Felipa would pay on a $95 dress.
Solution
88. Savings Ryan has 25% of each paycheck automatically deposited in his savings account.
a) Write 25% as a fraction.
b) Use your answer from (a) to find the amount that goes to savings from Ryan’s $2,400 paycheck.
Amelio is shopping for textbooks online. He found three sellers that are offering a book he needs for the same price, including shipping. To decide which seller to buy from he is comparing their customer satisfaction ratings. The ratings are given in the chart.
Use the chart to answer the following questions
| Seller | Rating |
|---|---|
89. Write seller C’s rating as (a) a fraction and (b) a decimal.
Solution
90. Write seller B’s rating as (a) a percent and (b) a decimal.
91. Write seller A’s rating as (a) a percent and (b) a decimal.
Solution
92. Which seller should Amelio buy from and why?
Writing Exercises
93. Convert 25%, 50%, 75%, and 100% to fractions. Do you notice a pattern? Explain what the pattern is.
94. Convert [latex]\frac{1}{10}, \frac{2}{10}, \frac{3}{10}, \frac{4}{10}, \frac{5}{10}, \frac{6}{10}, \frac{7}{10, \frac{8}{10}[/latex], and [latex]\frac{9}{10}[/latex] to percents. Do you notice a pattern? Explain what the pattern is.
95. When the Szetos sold their home, the selling price was 500% of what they had paid for the house 30 years ago. Explain what 500% means in this context.
96. According to cnn.com, cell phone use in 2008 was 600% of what it had been in 2001. Explain what 600% means in this context.
Practice Makes Perfect
Translate and Solve Basic Percent Equations
In the following exercises, translate and solve.
1. What number is 45% of 120?
Solution
54
2. What number is 65% of 100?
3. What number is 24% of 112?
Solution
26.9
4. What number is 36 of 124?
5. 250% of 65 is what number?
Solution
162.5
6. 150% of 90 is what number?
7. 800% of 2,250 is what number?
Solution
18,000
8. 600% of 1,740 is what number?
9. 28 is 25% of what number?
Solution
112
10. 36 is 25% of what number?
11. 81 is 75% of what number?
Solution
108
12. 93 is 75% of what number?
13. 8.2% of what number is $2.87?
Solution
$35
14. 6.4% of what number is $2.88?
15. 11.5% of what number is $108.10?
Solution
$940
16. 12.3% of what number is $92.25?
17. What percent of 260 is 78?
Solution
30%
18. What percent of 215 is 86?
19. What percent of 1,500 is 540?
Solution
36%
20. What percent of 1,800 is 846?
21. 30 is what percent of 20?
Solution
150%
22. 50 is what percent of 40?
23. 840 is what percent of 480?
Solution
175%
24. 790 is what percent of 395?
Solve Applications of Percents
In the following exercises, solve the applications of percents.
25. Geneva treated her parents to dinner at their favorite restaurant. The bill was $74.25. She wants to leave 16% of the total bill as a tip. How much should the tip be?
Solution
$11.88
26. When Hiro and his co-workers had lunch at a restaurant the bill was $90.50. The want to leave 18% of the total bill as a tip. How much should the tip be?
27. Trong has 12% of each paycheck automatically deposited to his savings account. His last paycheck was $2,165. How much money was deposited to Trong’s savings account?
Solution
$259.80
28. Cherise deposits 8% of each paycheck into her retirement account. Her last paycheck was $1,485. How much did Cherise deposit into her retirement account?
29. One serving of oatmeal has 8 grams of fiber, which is 33% of the recommended daily amount. What is the total recommended daily amount of fiber?
Solution
24.2 grams
30. One serving of trail mix has 67 grams of carbohydrates, which is 22% of the recommended daily amount. What is the total recommended daily amount of carbohydrates?
31. A bacon cheeseburger at a popular fast food restaurant contains 2,070 milligrams (mg) of sodium, which is 86% of the recommended daily amount. What is the total recommended daily amount of sodium?
Solution
2,407 mg
32. A grilled chicken salad at a popular fast food restaurant contains 650 milligrams (mg) of sodium, which is 27% of the recommended daily amount. What is the total recommended daily amount of sodium?
33. The nutrition fact sheet at a fast food restaurant says the fish sandwich has 380 calories, and 171 calories are from fat. What percent of the total calories is from fat?
Solution
45%
34. The nutrition fact sheet at a fast food restaurant says a small portion of chicken nuggets has 190 calories, and 114 calories are from fat. What percent of the total calories is from fat?
35. Emma gets paid $3,000 per month. She pays $750 a month for rent. What percent of her monthly pay goes to rent?
Solution
25%
36. Dimple gets paid $3,200 per month. She pays $960 a month for rent. What percent of her monthly pay goes to rent?
Find Percent Increase and Percent Decrease
In the following exercises, find the percent increase or percent decrease.
37. Tamanika got a raise in her hourly pay, from $15.50 to $17.55. Find the percent increase.
Solution
13.2%
38. Ayodele got a raise in her hourly pay, from $24.50 to $25.48. Find the percent increase.
39. Annual student fees at the University of California rose from about $4,000 in 2000 to about $9,000 in 2014. Find the percent increase.
Solution
125%
40. The price of a share of one stock rose from $12.50 to $50. Find the percent increase.
41. According to Time magazine (7/19/2011) annual global seafood consumption rose from 22 pounds per person in 1960 to 38 pounds per person today. Find the percent increase. (Round to the nearest tenth of a percent.)
Solution
72.7%
42. In one month, the median home price in the Northeast rose from $225,400 to $241,500. Find the percent increase. (Round to the nearest tenth of a percent.)
43. A grocery store reduced the price of a loaf of bread from $2.80 to $2.73. Find the percent decrease.
Solution
2.5%
44. The price of a share of one stock fell from $8.75 to $8.54. Find the percent decrease.
45. Hernando’s salary was $49,500 last year. This year his salary was cut to $44,055. Find the percent decrease.
Solution
11%
46. From 2000 to 2010, the population of Detroit fell from about 951,000 to about 714,000. Find the percent decrease. (Round to the nearest tenth of a percent.)
47. In one month, the median home price in the West fell from $203,400 to $192,300. Find the percent decrease. (Round to the nearest tenth of a percent.)
Solution
5.5%
48. Sales of video games and consoles fell from $1,150 million to $1,030 million in one year. Find the percent decrease. (Round to the nearest tenth of a percent.)
Everyday Math
49. Tipping At the campus coffee cart, a medium coffee costs $1.65. MaryAnne brings $2.00 with her when she buys a cup of coffee and leaves the change as a tip. What percent tip does she leave?
Solution
21.2%
50. Late Fees Alison was late paying her credit card bill of $249. She was charged a 5% late fee. What was the amount of the late fee?
Writing Exercises
51. Without solving the problem “44 is 80% of what number”, think about what the solution might be. Should it be a number that is greater than 44 or less than 44? Explain your reasoning.
Solution
Greater than 44
52. Without solving the problem “What is 20% of 300?” think about what the solution might be. Should it be a number that is greater than 300 or less than 300? Explain your reasoning.
53. After returning from vacation, Alex said he should have packed 50% fewer shorts and 200% more shirts. Explain what Alex meant.
Solution
He should have packed half as many shorts and twice as many shirts.
Glossary
-
- percent
- A percent is a ratio whose denominator is 100.
- discount
- An amount of discount is a percent off the original price, determined by the discount rate.
- mark-up
- The mark-up is the amount added to the wholesale price, determined by the mark-up rate.
percent decrease
The percent decrease is the percent the amount of decrease is of the original amount.
- percent increase
- The percent increase is the percent the amount of increase is of the original amount.
Media Attributions
- Figure 1 © Openstax is licensed under a CC BY (Attribution) license
- Figure 2 © Openstax is licensed under a CC BY (Attribution) license
- Figure 3 © Openstax is licensed under a CC BY (Attribution) license
- Figure 4 © Openstax is licensed under a CC BY (Attribution) license
- Figure 5 © Openstax is licensed under a CC BY (Attribution) license