"

2.2 Models and Applications

Cynthia Singleton; Ginny Bradley; Karen Perilloux; and Prakash Ghimire

Learning Objectives

In this section you will:

  • Approach word problems with a positive attitude
  • Use a problem solving strategy for word problems
  • Set up a linear equation to solve a real-world application.
  • Use a formula to solve a real-world application.
  • Solve number problems
  • Solve coin word problems.
  • Solve ticket and stamp word problems.

 

Approach Word Problems with a Positive Attitude

The world is full of word problems. How much money do I need to fill the car with gas? How much should I tip the server at a restaurant? How many socks should I pack for vacation? How big a turkey do I need to buy for Thanksgiving dinner, and what time do I need to put it in the oven? If my sister and I buy our mother a present, how much will each of us pay?

Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student in Figure 1 below?

A cartoon image of a girl with a confident expression holding some books is shown. There are 4 thought bubbles. They read, “While word problems were hard in the past, I think I can try them now,” then “I am better prepared now. I think I will begin to understand word problems,” then “I think I can! I think I can!,” and lastly, “It may take time, but I can begin to solve word problems.”
Figure 1. Negative thoughts about word problems can be barriers to success.

When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.

Start with a fresh slate and begin to think positive thoughts like the student in Figure 2 below. Read the positive thoughts and say them out loud.

A cartoon image of a girl with a confident expression holding some books is shown. There are 4 thought bubbles. They read, “While word problems were hard in the past, I think I can try them now,” then “I am better prepared now. I think I will begin to understand word problems,” then “I think I can! I think I can!,” and lastly, “It may take time, but I can begin to solve word problems.”
Figure 2. When it comes to word problems, a positive attitude is a big step toward success.

If we take control and believe we can be successful, we will be able to master word problems.

Think of something that you can do now but couldn’t do three years ago. Whether it’s driving a car, snowboarding, cooking a gourmet meal, or speaking a new language, you have been able to learn and master a new skill. Word problems are no different. Even if you have struggled with word problems in the past, you have acquired many new math skills that will help you succeed now!

Use a Problem-solving Strategy for Word Problems

In earlier chapters, you translated word phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. Since then you’ve increased your math vocabulary as you learned about more algebraic procedures, and you’ve had more practice translating from words into algebra.

You have also translated word sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. You had to restate the situation in one sentence, assign a variable, and then write an equation to solve. This method works as long as the situation is familiar to you and the math is not too complicated.

Now we’ll develop a strategy you can use to solve any word problem. This strategy will help you become successful with word problems. We’ll demonstrate the strategy as we solve the following problem.

Example

Pete bought a shirt on sale for $18, which is one-half the original price. What was the original price of the shirt?

Show Solution Step 1. Read the problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don’t understand, look them up in a dictionary or on the Internet.
  • In this problem, do you understand what is being discussed? Do you understand every word?

Step 2. Identify what you are looking for. It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!

  • In this problem, the words “what was the original price of the shirt” tell you that what you are looking for: the original price of the shirt.

Step 3. Name what you are looking for. Choose a variable to represent that quantity. You can use any letter for the variable, but it may help to choose one that helps you remember what it represents.

  • Let [latex]p[/latex] = the original price of the shirt
     

Step 4. Translate into an equation. It may help to first restate the problem in one sentence, with all the important information. Then translate the sentence into an equation.

The top line reads: “18 is one-half of the original price.” Below 18 is a brace and the number 18. Below “is” is a brace and an equal sign. Below “one-half” is a brace and the fraction 1 over 2. Below “of” is a brace and a multiplication dot. Below “the original price” is a brace and an italicized p.

Step 5. Solve the equation using good algebra techniques. Even if you know the answer right away, using algebra will better prepare you to solve problems that do not have obvious answers.

Write the equation. Eighteen equals one-half times P
Multiply both sides by 2. 2 multiplied by 18 equals 2 multiplied by one-half multiplied by P
Simplify. Thirty six equlas P

Step 6. Check the answer in the problem and make sure it makes sense.

  • We found that p=36, which means the original price was $36. Does $36 make sense in the problem?Yes, because 18 is one-half of 36, and the shirt was on sale at half the original price.

Step 7. Answer the question with a complete sentence.

  • The problem asked “What was the original price of the shirt?” The answer to the question is: “The original price of the shirt was $36.”

If this were a homework exercise, our work might look like this:

The top reads, “Let p equal the original price. 18 is one-half the original price.” The next line shows the equation 18 equals one-half times p. The following line shows the same equation with each side being multiplied by 2. The next line shows 36 equals p. Below this, it reads, “Check: Is $36 a reasonable price for a shirt? Yes. Is 18 one-half of 36? Yes. The original price of the shirt as $36.

Try It

Joaquin bought a bookcase on sale for $120, which was two-thirds the original price. What was the original price of the bookcase?

Show Solution

[latex]$ 180[/latex]

Try It

Two-fifths of the people in the senior center dining room are men. If there are 16 men, what is the total number of people in the dining room?

Show Solution

[latex]$ 40[/latex]

We list the steps we took to solve the previous example.

Problem-Solving Strategy

  • Step 1. Read the word problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don’t understand, look them up in a dictionary or on the internet.
  • Step 2. Identify what you are looking for.
  • Step 3. Name what you are looking for. Choose a variable to represent that quantity.
  • Step 4. Translate into an equation. It may be helpful to first restate the problem in one sentence before translating.
  • Step 5. Solve the equation using good algebra techniques.
  • Step 6. Check the answer in the problem. Make sure it makes sense.
  • Step 7. Answer the question with a complete sentence.

Let’s use this approach with another example.

Example

Yash brought apples and bananas to a picnic. The number of apples was three more than twice the number of bananas. Yash brought 11 apples to the picnic. How many bananas did he bring?

Show Solution
Step 1. Read the problem.
Step 2. Identify what you are looking for. How many bananas did he bring?
Step 3. Name what you are looking for.
Choose a variable to represent the number of bananas.		 Let

b=number of bananasb=number of bananas
Step 4. Translate. Restate the problem in one sentence with all the important information.
Translate into an equation.
Equation: Eleven equals three plus two multiplied by b
Step 5. Solve the equation. [latex]11 = 3 + 2b[/latex]
Subtract 3 from each side. [latex]11 -3  = 3 + 2b -3[/latex]
Simplify. [latex]8= 2b[/latex]
Divide each side by 2. [latex]frac{8}{2} = frac{2b}{2}[/latex]
Simplify. [latex]4 = b[/latex]
Step 6. Check: First, is our answer reasonable? Yes, bringing four bananas to a picnic seems reasonable. The problem says the number of apples was three more than twice the number of bananas. If there are four bananas, does that make eleven apples? Twice 4 bananas is 8. Three more than 8 is 11.
Step 7. Answer the question. Yash brought 4 bananas to the picnic.

Try It

Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was 3 more than the number of notebooks. He bought 5 textbooks. How many notebooks did he buy?

Show Solution

[latex]2  [/latex]

Try It

Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is seven more than the number of crossword puzzles. He completed 14 Sudoku puzzles. How many crossword puzzles did he complete?

Show Solution

[latex]7  [/latex]

In Solve Sales Tax, Commission, and Discount Applications, we learned how to translate and solve basic percent equations and used them to solve sales tax and commission applications. In the next example, we will apply our Problem Solving Strategy to more applications of percent.

Example

Nga’s car insurance premium increased by $60, which was 8% of the original cost. What was the original cost of the premium?

Show Solution
Step 1. Read the problem. Remember, if there are words you don’t understand, look them up.
Step 2. Identify what you are looking for. the original cost of the premium
Step 3. Name. Choose a variable to represent the original cost of premium. Let

c=the original costc=the original cost
Step 4. Translate. Restate as one sentence. Translate into an equation.
Equation: sixty equals 0.08 multiplied by c
Step 5. Solve the equation. [latex]60 = 0.08 c[/latex]
Divide both sides by 0.08. [latex]frac{60}{0.08} = frac{0.08 c}{0.08}[/latex]
Simplify. c=750c=750
Step 6. Check: Is our answer reasonable? Yes, a $750 premium on auto insurance is reasonable. Now let’s check our algebra. Is 8% of 750 equal to 60?
Equation: Seven hundred fifty equals c
Equation: 0.08 multiplied by Seven hundred fifty equals sixty
Equation: Sixt equals sixty
Step 7. Answer the question. The original cost of Nga’s premium was $750.

Try It

Pilar’s rent increased by 4%. The increase was $38. What was the original amount of Pilar’s rent?

Show Solution

[latex]$ 950  [/latex]

Try It

Steve saves 12% of his paycheck each month. If he saved $504 last month, how much was his paycheck?

Show Solution

[latex]$ 4,200  [/latex]

Access the online resource below for additional instruction and practice with solving word problems:

Setting up a Linear Equation to Solve a Real-World Application

Josh is hoping to get an A in his college algebra class. He has scores of 75, 82, 95, 91, and 94 on his first five tests. Only the final exam remains, and the maximum of points that can be earned is 100. Is it possible for Josh to end the course with an A? A simple linear equation will give Josh his answer.

Many students studying in a large lecture hall
Figure 1. Credit: Kevin Dooley
Many real-world applications can be modeled by linear equations. For example, a cell phone package may include a monthly service fee plus a charge per minute of talk-time; it costs a widget manufacturer a certain amount to produce x widgets per month plus monthly operating charges; a car rental company charges a daily fee plus an amount per mile driven. These are examples of applications we come across every day that are modeled by linear equations. In this section, we will set up and use linear equations to solve such problems.

To set up or model a linear equation to fit a real-world application, we must first determine the known quantities and define the unknown quantity as a variable. Then, we begin to interpret the words as mathematical expressions using mathematical symbols. Let us use the car rental example above. In this case, a known cost, such as $0.10/mi, is multiplied by an unknown quantity, the number of miles driven. Therefore, we can write[latex],0.10x.,[/latex]This expression represents a variable cost because it changes according to the number of miles driven.

If a quantity is independent of a variable, we usually just add or subtract it, according to the problem. As these amounts do not change, we call them fixed costs. Consider a car rental agency that charges $0.10/mi plus a daily fee of $50. We can use these quantities to model an equation that can be used to find the daily car rental cost[latex],C.[/latex]

[latex]C=0.10x+50[/latex]

When dealing with real-world applications, there are certain expressions that we can translate directly into math. Table 1 lists some common verbal expressions and their equivalent mathematical expressions.

Table 1

Verbal Translation to Math Operations
One number exceeds another by a [latex]x,text{​},x+a[/latex]
Twice a number [latex]2x[/latex]
One number is a more than another number [latex]x,text{​},x+a[/latex]
One number is a less than twice another number [latex]x,,2x-a[/latex]
The product of a number and a, decreased by b [latex]ax-b[/latex]
The quotient of a number and the number plus a is three times the number [latex]frac{x}{x+a}=3x[/latex]
The product of three times a number and the number decreased by b is c [latex]3xleft(x-bright)=c[/latex]

How To

Given a real-world problem, model a linear equation to fit it.

  1. Identify known quantities.
  2. Assign a variable to represent the unknown quantity.
  3. If there is more than one unknown quantity, find a way to write the second unknown in terms of the first.
  4. Write an equation interpreting the words as mathematical operations.
  5. Solve the equation. Be sure the solution can be explained in words, including the units of measure.

Modeling a Linear Equation to Solve an Unknown Number Problem

Modeling a Linear Equation to Solve an Unknown Number Problem

Find a linear equation to solve for the following unknown quantities: One number exceeds another number by[latex],17,[/latex]and their sum is[latex],31.,[/latex]Find the two numbers.

Show Solution

Let[latex],x,[/latex]equal the first number. Then, as the second number exceeds the first by 17, we can write the second number as[latex],x+17.,[/latex]The sum of the two numbers is 31. We usually interpret the word is as an equal sign.

[latex]begin{array}{ccc}hfill x+left(x+17right)& =& 31hfill \ hfill 2x+17& =& 31phantom{rule{2em}{0ex}}text{Simplify and solve}text{.}hfill \ hfill 2x& =& 14hfill \ hfill x& =& 7hfill \ phantom{rule{1em}{0ex}}hfill x+17& =& 7+17hfill \ & =& 24hfill end{array}[/latex]

The two numbers are[latex],7,[/latex]and[latex],24.[/latex]

 

Try It

Find a linear equation to solve for the following unknown quantities: One number is three more than twice another number. If the sum of the two numbers is[latex],36,[/latex] find the numbers.

Show Solution

11 and 25

Setting Up a Linear Equation to Solve a Real-World Application

There are two cell phone companies that offer different packages. Company A charges a monthly service fee of $34 plus $.05/min talk-time. Company B charges a monthly service fee of $40 plus $.04/min talk-time.

    1. Write a linear equation that models the packages offered by both companies.
    2. If the average number of minutes used each month is 1,160, which company offers the better plan?
    3. If the average number of minutes used each month is 420, which company offers the better plan?
    4. How many minutes of talk-time would yield equal monthly statements from both companies?
Show Solution
  1. The model for Company A can be written as[latex],A=0.05x+34.,[/latex]This includes the variable cost of[latex],0.05x,[/latex]plus the monthly service charge of $34. Company B’s package charges a higher monthly fee of $40, but a lower variable cost of[latex],0.04x.,[/latex]Company B’s model can be written as[latex],B=0.04x+text{$}40.[/latex]
  2. If the average number of minutes used each month is 1,160, we have the following:
    [latex]begin{array}{ccc}hfill text{Company }A& =& 0.05left(1.160right)+34hfill \ & =& 58+34hfill \ & =& 92hfill \ phantom{rule{1em}{0ex}}hfill text{Company }B& =& 0.04left(1,1600right)+40hfill \ & =& 46.4+40hfill \ hfill & =& 86.4hfill end{array}[/latex]

    So, Company B offers the lower monthly cost of $86.40 as compared with the $92 monthly cost offered by Company A when the average number of minutes used each month is 1,160.

  3. If the average number of minutes used each month is 420, we have the following:
    [latex]begin{array}{ccc}hfill text{Company }A& =& 0.05left(420right)+34hfill \ & =& 21+34hfill \ & =& 55hfill \ phantom{rule{1em}{0ex}}hfill text{Company }B& =& 0.04left(420right)+40hfill \ & =& 16.8+40hfill \ & =& 56.8hfill end{array}[/latex]

    If the average number of minutes used each month is 420, then Company A offers a lower monthly cost of $55 compared to Company B’s monthly cost of $56.80.

  4. To answer the question of how many talk-time minutes would yield the same bill from both companies, we should think about the problem in terms of[latex],left(x,yright),[/latex]coordinates: At what point are both the x-value and the y-value equal? We can find this point by setting the equations equal to each other and solving for x.
    [latex]begin{array}{ccc}hfill 0.05x+34& =& 0.04x+40hfill \ hfill 0.01x& =& 6hfill \ hfill x& =& 600hfill end{array}[/latex]

    Check the x-value in each equation.

    [latex]begin{array}{ccc}hfill 0.05left(600right)+34& =& 64hfill \ hfill 0.04left(600right)+40& =& 64hfill end{array}[/latex]

    Therefore, a monthly average of 600 talk-time minutes renders the plans equal. See Figure 2.

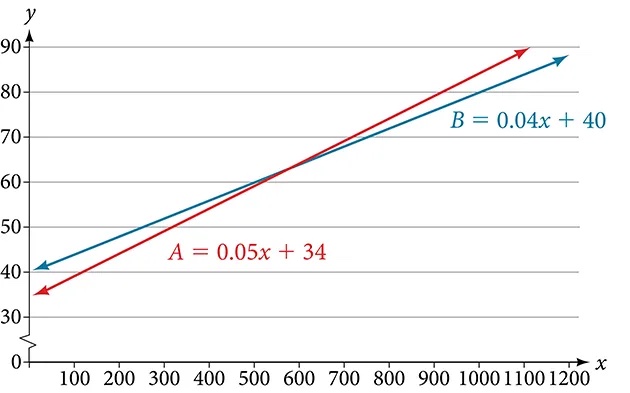
    Coordinate plane with the x-axis ranging from 0 to 1200 in intervals of 100 and the y-axis ranging from 0 to 90 in intervals of 10. The functions A = 0.05x + 34 and B = 0.04x + 40 are graphed on the same plot
    Figure 2.

 

Try It

Find a linear equation to model this real-world application: It costs ABC electronics company $2.50 per unit to produce a part used in a popular brand of desktop computers. The company has monthly operating expenses of $350 for utilities and $3,300 for salaries. What are the company’s monthly expenses?

Show Solution

[latex]C=2.5x+3,650[/latex]

Using a Formula to Solve a Real-World Application

Many applications are solved using known formulas. The problem is stated, a formula is identified, the known quantities are substituted into the formula, the equation is solved for the unknown, and the problem’s question is answered. Typically, these problems involve two equations representing two trips, two investments, two areas, and so on. Examples of formulas include the area of a rectangular region,[latex],A=LW;[/latex] the perimeter of a rectangle,[latex],P=2L+2W;[/latex] and the volume of a rectangular solid,[latex],V=LWH.,[/latex]When there are two unknowns, we find a way to write one in terms of the other because we can solve for only one variable at a time.

Solving an Application Using a Formula

It takes Andrew 30 min to drive to work in the morning. He drives home using the same route, but it takes 10 min longer, and he averages 10 mi/h less than in the morning. How far does Andrew drive to work?

Show Solution

This is a distance problem, so we can use the formula[latex],d=rt,[/latex]where distance equals rate multiplied by time. Note that when rate is given in mi/h, time must be expressed in hours. Consistent units of measurement are key to obtaining a correct solution.

First, we identify the known and unknown quantities. Andrew’s morning drive to work takes 30 min, or[latex],frac{1}{2},[/latex]h at rate[latex],r.,[/latex]His drive home takes 40 min, or[latex],frac{2}{3},[/latex]h, and his speed averages 10 mi/h less than the morning drive. Both trips cover distance[latex],d.,[/latex]A table, such as Figure 3, is often helpful for keeping track of information in these types of problems.

Figure 3

[latex]d[/latex] [latex]r[/latex] [latex]t[/latex]
To Work [latex]d[/latex] [latex]r[/latex] [latex]frac{1}{2}[/latex]
To Home [latex]d[/latex] [latex]r-10[/latex] [latex]frac{2}{3}[/latex]

Write two equations, one for each trip.

[latex]begin{array}{cccc}hfill d& =& rleft(frac{1}{2}right)hfill & phantom{rule{2em}{0ex}}text{To work}hfill \ hfill d& =& left(r-10right)left(frac{2}{3}right)hfill & phantom{rule{2em}{0ex}}text{To home}hfill end{array}[/latex]

As both equations equal the same distance, we set them equal to each other and solve for r.

[latex]begin{array}{ccc}hfill rleft(frac{1}{2}right)& =& left(r-10right)left(frac{2}{3}right)hfill \ hfill frac{1}{2r}& =& frac{2}{3}r-frac{20}{3}hfill \ hfill frac{1}{2}r-frac{2}{3}r& =& -frac{20}{3}hfill \ hfill -frac{1}{6}r& =& -frac{20}{3}hfill \ hfill r& =& -frac{20}{3}left(-6right)hfill \ hfill r& =& 40hfill end{array}[/latex]

We have solved for the rate of speed to work, 40 mph. Substituting 40 into the rate on the return trip yields 30 mi/h. Now we can answer the question. Substitute the rate back into either equation and solve for d.

[latex]begin{array}{ccc}hfill d& =& 40left(frac{1}{2}right)hfill \ & =& 20hfill end{array}[/latex]

The distance between home and work is 20 mi.

Analysis

Note that we could have cleared the fractions in the equation by multiplying both sides of the equation by the LCD to solve for[latex],r.[/latex]

[latex]begin{array}{ccc}hfill rleft(frac{1}{2}right)& =& left(r-10right)left(frac{2}{3}right)hfill \ hfill 6text{ }×text{ }rleft(frac{1}{2}right)& =& 6text{ }×text{ }left(r-10right)left(frac{2}{3}right)hfill \ hfill 3r& =& 4left(r-10right)hfill \ hfill 3r& =& 4r-40hfill \ hfill -r& =& -40hfill \ hfill r& =& 40hfill end{array}[/latex]

 

Try It

On Saturday morning, it took Jennifer 3.6 h to drive to her mother’s house for the weekend. On Sunday evening, due to heavy traffic, it took Jennifer 4 h to return home. Her speed was 5 mi/h slower on Sunday than on Saturday. What was her speed on Sunday?

Show Solution

45 mi/h

Solving a Perimeter Problem

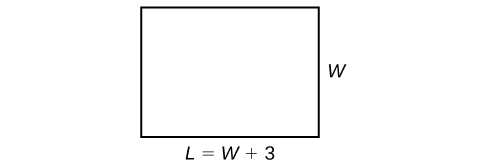
The perimeter of a rectangular outdoor patio is[latex],54,[/latex]ft. The length is[latex],3,[/latex]ft greater than the width. What are the dimensions of the patio?

Show Solution

The perimeter formula is standard:[latex],P=2L+2W.,[/latex]We have two unknown quantities, length and width. However, we can write the length in terms of the width as[latex],L=W+3.,[/latex]Substitute the perimeter value and the expression for length into the formula. It is often helpful to make a sketch and label the sides, as in Figure 3.

A rectangle with the length labeled as: L = W + 3 and the width labeled as: W.
Figure 3

Now we can solve for the width and then calculate the length.

[latex]begin{array}{ccc}hfill P& =& 2L+2Whfill \ hfill 54& =& 2left(W+3right)+2Whfill \ hfill 54& =& 2W+6+2Whfill \ hfill 54& =& 4W+6hfill \ hfill 48& =& 4Whfill \ hfill 12& =& Whfill \ hfill left(12+3right)& =& Lhfill \ hfill 15& =& Lhfill end{array}[/latex]

The dimensions are[latex],L=15,[/latex]ft and[latex],W=12,[/latex]ft.

 

Try It

Find the dimensions of a rectangle given that the perimeter is[latex],110,[/latex]cm and the length is 1 cm more than twice the width.

Show Solution

[latex]L=37,[/latex]cm,[latex],W=18,[/latex]cm

Solving an Area Problem

The perimeter of a tablet of graph paper is 48 in. The length is[latex],6,[/latex]in. more than the width. Find the area of the graph paper.

Show Solution

The standard formula for area is[latex],A=LW;[/latex] however, we will solve the problem using the perimeter formula. The reason we use the perimeter formula is because we know enough information about the perimeter that the formula will allow us to solve for one of the unknowns. As both perimeter and area use length and width as dimensions, they are often used together to solve a problem such as this one.

We know that the length is 6 in. more than the width, so we can write length as[latex],L=W+6.,[/latex]Substitute the value of the perimeter and the expression for length into the perimeter formula and find the length.

[latex]begin{array}{ccc}hfill P& =& 2L+2Whfill \ hfill 48& =& 2left(W+6right)+2Whfill \ hfill 48& =& 2W+12+2Whfill \ hfill 48& =& 4W+12hfill \ hfill 36& =& 4Whfill \ hfill 9& =& Whfill \ hfill left(9+6right)& =& Lhfill \ hfill 15& =& Lhfill end{array}[/latex]

Now, we find the area given the dimensions of[latex],L=15,[/latex]in. and[latex],W=9,[/latex]in.

[latex]begin{array}{ccc}hfill A& =& LWhfill \ hfill A& =& 15left(9right)hfill \ & =& hfill 135text{ in}{text{.}}^{2}end{array}[/latex]

The area is[latex],135,[/latex]in.2.

 

Try It

A game room has a perimeter of 70 ft. The length is five more than twice the width. How many ft2 of new carpeting should be ordered?

Show Solution

250 ft2

Solving a Volume Problem

Find the dimensions of a shipping box given that the length is twice the width, the height is[latex],8,[/latex]inches, and the volume is 1,600 in.3.

Show Solution

The formula for the volume of a box is given as[latex],V=LWH,[/latex] the product of length, width, and height. We are given that[latex],L=2W[/latex] and[latex],H=8.,[/latex]The volume is[latex],1,600,[/latex]cubic inches.

[latex]begin{array}{ccc}hfill V& =& LWHhfill \ hfill 1,600& =& left(2Wright)Wleft(8right)hfill \ hfill 1,600& =& 16{W}^{2}hfill \ hfill 100& =& {W}^{2}hfill \ hfill 10& =& Whfill end{array}[/latex]

The dimensions are[latex],L=20,[/latex]in.,[latex],W=10,[/latex]in., and[latex],H=8,[/latex]in.

Analysis

Note that the square root of[latex],{W}^{2},[/latex]would result in a positive and a negative value. However, because we are describing width, we can use only the positive result.

 

Solve Number Problems

Now we will translate and solve number problems. In number problems, you are given some clues about one or more numbers, and you use these clues to build an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the Problem Solving Strategy. Remember to look for clue words such as difference, of, and and.

Example

The difference of a number and six is 13. Find the number.

Show Solution
Step 1. Read the problem. Do you understand all the words?
Step 2. Identify what you are looking for. the number
Step 3. Name. Choose a variable to represent the number. Let n=the numbern=the number
Step 4. Translate. Restate as one sentence.
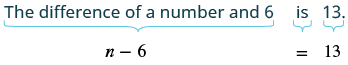 Translate into an equation.		 Equation: n minus six equals thirteen
Step 5. Solve the equation.
Add 6 to both sides.
Simplify.		 Equation: n minus six equals thirteen
Equation: n minus six plus six equals thirteen plus six
Equation: n equals nineteen
Step 6. Check:
The difference of 19 and 6 is 13. It checks.
Step 7. Answer the question. The number is 19.

Try It

The difference of a number and eight is 17. Find the number.

Show Solution

[latex]25  [/latex]

Try It

The difference of a number and eleven is −7. Find the number.

Show Solution

[latex]4  [/latex]

Example

The sum of twice a number and seven is 15. Find the number.

Show Solution
Step 1. Read the problem.
Step 2. Identify what you are looking for. the number
Step 3. Name. Choose a variable to represent the number. Let n = the number
Step 4. Translate. Restate the problem as one sentence.
 Translate into an equation.		 Equation: two multiplied by n plus seven equals fifteen
Step 5. Solve the equation. Equation: two multiplied by n plus seven equals fifteen
Subtract 7 from each side and simplify. Equation: two multiplied by n equals eight
Divide each side by 2 and simplify. Equation: n equals four
Step 6. Check: is the sum of twice 4 and 7 equal to 15?
Equation: two multiplied by four plus seven equals fifteen
Equation: Eight plus seven equals fifteen
Equation: fifteen equals fifteen
Step 7. Answer the question. The number is 4.

Try It

The sum of four times a number and two is 14. Find the number.

Show Solution

[latex]3  [/latex]

Try It

The sum of three times a number and seven is 25. Find the number.

Show Solution

[latex]6  [/latex]

Some number word problems ask you to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. We will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.

Example

One number is five more than another. The sum of the numbers is twenty-one. Find the numbers.

Show Solution
Step 1. Read the problem.
Step 2. Identify what you are looking for. You are looking for two numbers.
Step 3. Name.
Choose a variable to represent the first number.
What do you know about the second number?
Translate.
Let

n=1st numbern=1st number


One number is five more than another.

n+5=2ndnumbern+5=2ndnumber

Step 4. Translate.
Restate the problem as one sentence with all the important information.
Translate into an equation.
Substitute the variable expressions.
The sum of the numbers is 21.
The sum of the 1st number and the 2nd number is 21.
Equation: n plus n plus five equals twenty-oneStep 5. Solve the equation.Equation: n plus n plus five equals twenty-oneCombine like terms.Equation: two multiplied by n plus five equals twenty-oneSubtract five from both sides and simplify.Equation: two multiplied by n equals sixteenDivide by two and simplify.Equation: n equals eight first numberFind the second number too.n plus five second numberSubstitute n = 8n plus five
[latex]13[/latex]Step 6. Check:
Do these numbers check in the problem?
Is one number 5 more than the other?
Is thirteen, 5 more than 8? Yes.

Is the sum of the two numbers 21?Equation: Thirteen equlas question mark eight plus five
Equation: Thirteen equlas thirteen check mark

Equation: Eight plus Thirteen equlas question mark twenty one
Equation: Twently one equals twenty one check markStep 7. Answer the question.The numbers are 8 and 13.

Try It

One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.

Show Solution

[latex]9, 15  [/latex]

Try It

The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.

Show Solution

[latex]27,  31  [/latex]

Example

The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.

Show Solution
Step 1. Read the problem.
Step 2. Identify what you are looking for. two numbers
Step 3. Name. Choose a variable.
What do you know about the second number?
Translate.
Let n = 1st number
One number is 4 less than the other.
n – 4 = 2nd number
Step 4. Translate.
Write as one sentence.
Translate into an equation.
Substitute the variable expressions.
The sum of two numbers is negative fourteen.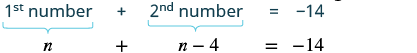
.
Step 5. Solve the equation. Equation: n plus n minus four equals negative fourteen
Combine like terms. Equation: two multiplied by n minus four equals negative fourteen
Add 4 to each side and simplify. Equation: Two multiplied by n equals negative ten
Divide by 2. Equation: n equals negative five first number
Substitute

n=−5n=−5to find the 2nd number.

 Equation: n minus four second number
negative five negative four
Negative nine
Step 6. Check:
Is −9 four less than −5?


Is their sum −14?		 Equation: Negative five minus four equlas question mark negative nine
Equation: Negative nine equlas negative nine check mark
Equation: Negative five plus negative nine equlas question mark negative fourteen
Equation: Negative fourteen equlas negative fourteen check mark
Step 7. Answer the question. The numbers are −5 and −9.

Try It

The sum of two numbers is negative twenty-three. One number is 7 less than the other. Find the numbers.

Show Solution

[latex]-8, -15  [/latex]

Try It

The sum of two numbers is negative eighteen. One number is 40 more than the other. Find the numbers.

Show Solution

[latex]-29, 11  [/latex]

Example

One number is ten more than twice another. Their sum is one. Find the numbers.

Show Solution
Step 1. Read the problem.
Step 2. Identify what you are looking for. two numbers
Step 3. Name. Choose a variable.
One number is ten more than twice another.		 Let x = 1st number
2x + 10 = 2nd number
Step 4. Translate. Restate as one sentence. Their sum is one.
Translate into an equation Equation: x plux two times x plus ten equals one
Step 5. Solve the equation. [latex]x + ( 2x +10) = 1  [/latex]
Combine like terms. [latex]3x +10 = 1  [/latex]
Subtract 10 from each side. [latex]3x = -9  [/latex]
Divide each side by 3 to get the first number. [latex]x = -  3[/latex]
Substitute to get the second number. [latex]2x + 10  [/latex]
[latex]2 ( -3) +10  [/latex]
[latex]4[/latex]
Step 6. Check.
Is 4 ten more than twice −3?



Is their sum 1?		 Equation: Two multiplied by negative three plus ten equlas question mark four


.
Equation: Four equals four check mark
Equation: negative three plus four equlas question mark one
Equation: one equals one check mark
Step 7. Answer the question. The numbers are −3 and 4.

Try It

One number is eight more than twice another. Their sum is negative four. Find the numbers.

Show Solution

[latex]-4, 0  [/latex]

Try It

One number is three more than three times another. Their sum is negative five. Find the numbers.

Show Solution

[latex]-2, -3  [/latex]

Consecutive integers are integers that immediately follow each other. Some examples of consecutive integers are:

[latex]cdots 1, 2, 3, 4, cdots[/latex]

[latex]cdots -10, -9, -8, -7, cdots[/latex]

[latex]cdots 150, 151, 152, 153, cdots[/latex]

Notice that each number is one more than the number preceding it. So if we define the first integer as [latex]n[/latex], the next consecutive integer is [latex]n+1[/latex]. The one after that one more than [latex]n+1[/latex], so it is [latex]n+1 +1[/latex] or [latex]n+2[/latex].

[latex]n   text{1st integer}[/latex]

[latex]n +1 text{2nd consecutive integer}[/latex]

[latex]n +2 text{3rd consecutive integer}[/latex]

Example

The sum of two consecutive integers is 47. Find the numbers.

Show Solution
Step 1. Read the problem.
Step 2. Identify what you are looking for. two consecutive integers
Step 3. Name. Let n = 1st integer
n + 1 = next consecutive integer
Step 4. Translate.
Restate as one sentence.
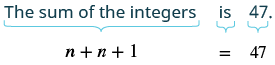Translate into an equation.		 Equation: n plus n plus one equals fourty seven
Step 5. Solve the equation. [latex]n + n +1 = 47  [/latex]
Combine like terms. [latex]2n +1 = 47  [/latex]
Subtract 1 from each side. [latex]2n  = 46  [/latex]
Divide each side by 2. [latex]n  = 23      text { 1st integer}  [/latex]
Substitute to get the second number. [latex]n +1      text { 2nd integer}  [/latex]
[latex]23 + 1[/latex]
[latex]24[/latex]
Step 6. Check: Equation: Twenty three plus twenty four equlas question mark fourty seven
Equation: Fourty seven equlas fourty seven
Step 7. Answer the question. The two consecutive integers are 23 and 24.

Try It

The sum of two consecutive integers is 95. Find the numbers.

Show Solution

[latex]47, 48  [/latex]

Try It

The sum of two consecutive integers is −31. Find the numbers.

Show Solution

[latex]-15, -16  [/latex]

Access the online resource below for additional instruction and practice with solving number problems:

Example

Find three consecutive integers whose sum is 42.

Show Solution
Step 1. Read the problem.
Step 2. Identify what you are looking for. three consecutive integers
Step 3. Name. Let n = 1st integer
n + 1 = 2nd consecutive integer
n + 2 = 3rd consecutive integer
Step 4. Translate.
Restate as one sentence.
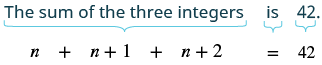Translate into an equation.		 Equation: n plus n plus one n plus two equals fourty two
Step 5. Solve the equation. [latex]n + n +1 + n + 2= 42  [/latex]
Combine like terms. [latex]3n + 3= 42  [/latex]
Subtract 3 from each side. [latex]3n = 39  [/latex]
Divide each side by 3. [latex]n  = 13      text { 1st integer}  [/latex]
Substitute to get the second number. [latex]n  +1        text { 2nd integer}  [/latex]
[latex]13 + 1  [/latex]
[latex]14  [/latex]
Substitute to get the third number. [latex]n  +2        text { 3rd integer}  [/latex]
[latex]13 + 2  [/latex]
[latex]15  [/latex]
Step 6. Check: Equation: Thirteen plus fourteen plus fifteen equlas question mark fourty two
Equation: fourty two equlas fourty two check mark
Step 7. Answer the question. The three consecutive integers are 13, 14, and 15.

Try It

Find three consecutive integers whose sum is 96.

Show Solution

[latex]31, 32, 33  [/latex]

Try It

Find three consecutive integers whose sum is −36.

Show Solution

[latex]-11, -12, -13  [/latex]

Solve Coin Word Problems

Imagine taking a handful of coins from your pocket or purse and placing them on your desk. How would you determine the value of that pile of coins?

If you can form a step-by-step plan for finding the total value of the coins, it will help you as you begin solving coin word problems.

One way to bring some order to the mess of coins would be to separate the coins into stacks according to their value. Quarters would go with quarters, dimes with dimes, nickels with nickels, and so on. To get the total value of all the coins, you would add the total value of each pile.

An image of a large stack of pennies, a large stack of nickels, a shorter stack of dimes, and a stack of quarters is shown. There are several coins in the background.
Figure 1 To determine the total value of a stack of nickels, multiply the number of nickels times the value of one nickel.(Credit: Darren Hester via ppdigital)

How would you determine the value of each pile? Think about the dime pile—how much is it worth? If you count the number of dimes, you’ll know how many you have—the number of dimes.

But this does not tell you the value of all the dimes. Say you counted 17dimes, how much are they worth? Each dime is worth $0.10— that is the value of one dime. To find the total value of the pile of 17dimes, multiply 17by $0.10to get $1.70.  This is the total value of all 17dimes.

17·$0.10=$1.70number·value=total value17·$0.10=$1.70number·value=total value

Total Value of Coins of the Same Type

For coins of the same type, the total value can be found as follows:

number·value=total valuenumber·value=total value

where [latex]text{number}[/latex] is the number of coins, [latex]text{value}[/latex] is the value of each coin, and [latex]text{total value}[/latex] is the total value of all the coins.

You could continue this process for each type of coin, and then you would know the total value of each type of coin. To get the total value of all the coins, add the total value of each type of coin.

Let’s look at a specific case.

Total Value of Coins of Different Types

Suppose there are 14 quarters, 17 dimes, 21 nickels, and 39 pennies. We’ll make a table to organize the information – the type of coin, the number of each, and the value.

Table 1
Type NumberNumber Value ($)Value ($) Total Value ($)Total Value ($)
Quarters 1414 0.250.25 3.503.50
Dimes 1717 0.100.10 1.701.70
Nickels 2121 0.050.05 1.051.05
Pennies 3939 0.010.01 0.390.39
6.646.64

The total value of all the coins is $6.64.

Notice how Table 1 helped us organize all the information. Let’s see how this method is used to solve a coin word problem.

Example

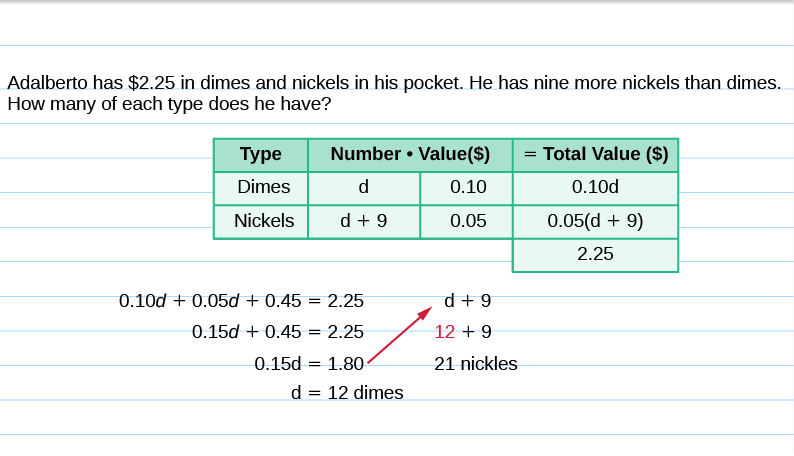
Adalberto has $2.25 in dimes and nickels in his pocket. He has nine more nickels than dimes. How many of each type of coin does he have?

Show Solution

Step 1. Read the problem. Make sure you understand all the words and ideas.

  • Determine the types of coins involved.

Think about the strategy we used to find the value of the handful of coins. The first thing you need is to notice what types of coins are involved. Adalberto has dimes and nickels.

  • Create a table to organize the information.
    • Label the columns ‘type’, ‘number’, ‘value’, ‘total value’.
    • List the types of coins.
    • Write in the value of each type of coin.
    • Write in the total value of all the coins.

We can work this problem all in cents or in dollars. Here we will do it in dollars and put in the dollar sign ($) in the table as a reminder.

The value of a dime is $0.10 and the value of a nickel is $0.05.  The total value of all the coins is $2.25.

Type NumberNumber Value ($)Value ($) Total Value ($)Total Value ($)
Dimes 0.100.10
Nickels 0.050.05
2.252.25

Step 2. Identify what you are looking for.

  • We are asked to find the number of dimes and nickels Adalberto has.

Step 3. Name what you are looking for.

  • Use variable expressions to represent the number of each type of coin.
  • Multiply the number times the value to get the total value of each type of coin.

    In this problem you cannot count each type of coin—that is what you are looking for—but you have a clue. There are nine more nickels than dimes. The number of nickels is nine more than the number of dimes.

Let d= number of dimes.
d+9 = number of nickels.
Fill in the “number” column to help get everything organized.

Type NumberNumber Value ($)Value ($) Total Value ($)Total Value ($)
Dimes dd 0.100.10 0.10d
Nickels d+9d+9 0.050.05 0.05(d+9)
2.252.25

Now we have all the information we need from the problem!

You multiply the number times the value to get the total value of each type of coin. While you do not know the actual number, you do have an expression to represent it.

And so now multiply [latex]text{number }cdottext{ value}[/latex] and write the results in the Total Value column.

Type NumberNumber Value ($)Value ($) Total Value ($)Total Value ($)
Dimes dd 0.100.10 0.10d0.10d
Nickels d+9d+9 0.050.05 0.05(d+9)0.05(d+9)
2.252.25

Step 4. Translate into an equation. Restate the problem in one sentence. Then translate into an equation.

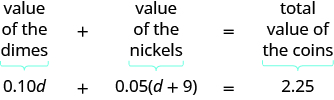
The sentence “Sum of the value of the dimes and value of the nickels is total value of the coins,” is written. Below “value of the dimes” is 0.10d. Below “and” is a plus sign. Below “value of the nickels” is 0.05(d plus 9). Below “is” is an equal sign. Below “total value of the coins” is 2.25.

Step 5. Solve the equation using good algebra techniques.

Write the equation. [latex]0.10d+0.05(d+9)=2.25[/latex]  
Distribute. [latex]0.10d+0.05d+.045=2.25[/latex]
Combine like terms. [latex]0.15d+0.45=2.25[/latex] 
Subtract 0.45 from each side. [latex]0.15d=1.80[/latex] 
Divide to find the number of dimes. [latex]d=12[/latex] 
The number of nickels is d + 9 [latex]d+9[/latex]
[latex]12+9=21[/latex]  

Step 6. Check.

12dimes:12(0.10)=1.2021nickels:21(0.05)=1.05_____$2.25✓Step 7. Answer the question.

Adalberto has twelve dimes and twenty-one nickels.

If this were a homework exercise, our work might look like this:

How many of each type does he have?” Below this is a table with 4 rows and 4 columns. The first row is a header row. The headings are, “Type”, “Number”, “Value ($)”, and “Total Value ($)” Under the “Type” column are the entries dimes and nickels. Under the “Number”,column are d and d plus 9. Under the “Value”,column are the values 0.10 and 0.05. Under the “Total Value”,column are 0.10d and 0.05(d plus 9) followed by 2.25. Below the table is the word “nickels”,in bold. The equation 0.10d plus 0.05(d plus 9) equals 2.25 is shown. Below that are 2 columns. The left column says 0.10d plus 0.05d plus 0.45 equals 2.25, then 0.15d plus 0.45 equals 2.25, then 0.15d equals 1.80, then d equals 12 dimes. There is a red arrow pointing to the right column. The right column says d plus 9, then a red 12 plus 9, then 21 nickels.

Adalberto has twelve dimes and twenty-one nickels.

Try It

Michaela has $2.05 in dimes and nickels in her change purse. She has seven more dimes than nickels. How many coins of each type does she have?

Show Solution

Michaela has 16 dimes and 9 nickels.

Try It

Liliana has $2.10 in nickels and quarters in her backpack. She has 12 more nickels than quarters. How many coins of each type does she have?

Show Solution

Liliana has 17 nickels and 5 quarters.

How To

Solve a coin word problem.

Step 1.  Read the problem. Make sure you understand all the words and ideas, and create a table to organize the information.

Step 2.  Identify what you are looking for.

Step 3.  Name what you are looking for. Choose a variable to represent that quantity.

  • Use variable expressions to represent the number of each type of coin and write them in the table.
  • Multiply the number times the value to get the total value of each type of coin.

Step 4.  Translate into an equation. Write the equation by adding the total values of all the types of coins.

Step 5.  Solve the equation using good algebra techniques.

Step 6.  Check the answer in the problem and make sure it makes sense.

Step 7.  Answer the question with a complete sentence.

You may find it helpful to put all the numbers into the table to make sure they check.

Table 2
Type Number Value ($) Total Value

Example

Maria has $2.43 in quarters and pennies in her wallet. She has twice as many pennies as quarters. How many coins of each type does she have?

Show Solution
  • Label the columns: type, number, value, total value.
  • List the types of coins.
  • Write in the value of each type of coin.
  • Write in the total value of all the coins.
Type NumberNumber Value ($)Value ($) Total Value ($)Total Value ($)
Quarters 0.250.25
Pennies 0.010.01
2.432.43

Step 2. Identify what you are looking for: We are looking for the number of quarters and pennies.

Step 3. Name: Represent the number of quarters and pennies using variables.:

We know Maria has twice as many pennies as quarters. The number of pennies is defined in terms of quarters.

Let [latex]q[/latex] represent the number of quarters.

Then the number of pennies is [latex]2q[/latex].

Type NumberNumber Value ($)Value ($) Total Value ($)Total Value ($)
Quarters qq 0.250.25
Pennies 2q2q 0.010.01
2.432.43

Multiply the ‘number’ and the ‘value’ to get the ‘total value’ of each type of coin.

Type NumberNumber Value ($)Value ($) Total Value ($)Total Value ($)
Quarters qq 0.250.25 0.25q0.25q
Pennies 2q2q 0.010.01 0.01(2q)0.01(2q)
2.432.43

Step 4. Translate.
Write the equation by adding the ‘total value’ of all the types of coins.

Step 5. Solve the equation.

Write the equation. [latex]0.25q+0.01(2q)=2.43[/latex]
Multiply. [latex]0.25q+0.02q=2.43[/latex]
Combine like terms. [latex].027q=2.43[/latex]
Divide by 0.27. [latex]q=9[/latex] quarters
The number of pennies is 2q. [latex]2q = 2 cdot 9 = 18[/latex] pennies
Step 6. Check:
Maria has 9 quarters and 18 pennies. Does this make $2.43?
9 quarters9(0.25)=2.2518 pennies18(0.01)=0.18_____Total$2.43✓
 
Step 7. Answer the question: Maria has nine quarters and eighteen pennies.

Try It

Sumanta has $4.20 in nickels and dimes in her desk drawer. She has twice as many nickels as dimes. How many coins of each type does she have?

Show Solution

Sumanta has 42 nickels and 21 dimes.

Try It

Alison has three times as many dimes as quarters in her purse. She has $9.35 altogether. How many coins of each type does she have?

Show Solution

Alison has 51 dimes and 17 quarters.

In the next example, we’ll show only the completed table—make sure you understand how to fill it in step by step.

Example

Danny has $2.14 worth of pennies and nickels in his piggy bank. The number of nickels is two more than ten times the number of pennies. How many nickels and how many pennies does Danny have?

Show Solution

Try It

Jesse has $6.55 worth of quarters and nickels in his pocket. The number of nickels is five more than two times the number of quarters. How many nickels and how many quarters does Jesse have?

Show Solution

Jesse has 41 nickels and 18 quarters.

Try It

Elaine has $7.00 in dimes and nickels in her coin jar. The number of dimes that Elaine has is seven less than three times the number of nickels. How many of each coin does Elaine have?

Show Solution

Elaine has 22 nickels and 59 dimes.

Solve Ticket and Stamp Word Problems

The strategies we used for coin problems can be easily applied to some other kinds of problems too. Problems involving tickets or stamps are very similar to coin problems, for example. Like coins, tickets and stamps have different values; so we can organize the information in tables much like we did for coin problems.

Example

At a school concert, the total value of tickets sold was $1,506.

Student tickets sold for $6 each and adult tickets sold for $9 each. The number of adult tickets sold was 5 less than three times the number of student tickets sold. How many student tickets and how many adult tickets were sold?

Show Solution

Try It

The first day of a water polo tournament, the total value of tickets sold was $17,610.  One-day passes sold for $20 and tournament passes sold for $30.

$30.The number of tournament passes sold was 37 more than the number of day passes sold. How many day passes and how many tournament passes were sold?

Show Solution

330 one-day passes and 367 tournament passes were sold.

Try It

At the movie theater, the total value of tickets sold was $2,612.50.

Adult tickets sold for $10 each and senior/child tickets sold for $7.50 each. The number of senior/child tickets sold was 25 less than twice the number of adult tickets sold. How many senior/child tickets and how many adult tickets were sold?

Show Solution

199 senior/child tickets and 112 adult tickets were sold.

Now we’ll do one where we fill in the table all at once.

Example

Monica paid $10.44 for stamps she needed to mail the invitations to her sister’s baby shower. The number of 49-cent stamps was four more than twice the number of 8-cent stamps. How many 49-cent stamps and how many 8-cent stamps did Monica buy?

Show Solution

Try It 

Eric paid $16.64 for stamps so he could mail thank you notes for his wedding gifts. The number of 49-cent stamps was eight more than twice the number of 8-cent stamps. How many 49-cent stamps and how many 8-cent stamps did Eric buy?

Show Solution

Eric bought thirty-two 49-cent stamps and twelve 8-cent stamps.

Try It 

Kailee paid $14.84 for stamps. The number of 49-cent stamps was four less than three times the number of 21-cent stamps. How many 49-cent stamps and how many 21-cent stamps did Kailee buy?

Show Solution

Kailee bought twenty-six 49-cent stamps and ten 21-cent stamps.

 

Key Concepts

Problem-Solving Strategy

  • Step 1. Read the word problem. Make sure you understand all the words and ideas. You may need to read the problem two or more times. If there are words you don’t understand, look them up in a dictionary or on the internet.
  • Step 2. Identify what you are looking for.
  • Step 3. Name what you are looking for. Choose a variable to represent that quantity.
  • Step 4. Translate into an equation. It may be helpful to first restate the problem in one sentence before translating.
  • Step 5. Solve the equation using good algebra techniques.
  • Step 6. Check the answer in the problem. Make sure it makes sense.
  • Step 7. Answer the question with a complete sentence.
  • A linear equation can be used to solve for an unknown in a number problem.
  • Applications can be written as mathematical problems by identifying known quantities and assigning a variable to unknown quantities.
  • There are many known formulas that can be used to solve applications. Distance problems, for example, are solved using the[latex]\,d=rt\,[/latex]formula.
  • Many geometry problems are solved using the perimeter formula[latex]\,P=2L+2W,[/latex]the area formula[latex]\,A=LW,[/latex] or the volume formula[latex]\,V=LWH.\,[/latex]

Finding the Total Value for Coins of the Same Type

For coins of the same type, the total value can be found as follows:

$$\text{number} \cdot \text{value} = \text{total value}$$
where number is the number of coins, value is the value of each coin, and total value is the total value of all the coins.

Solve a Coin Word Problem

  • Step 1. Read the problem. Make sure you understand all the words and ideas, and create a table to organize the information.
  • Step 2. Identify what you are looking for.
  • Step 3. Name what you are looking for. Choose a variable to represent that quantity.
    • Use variable expressions to represent the number of each type of coin and write them in the table.
    • Multiply the number times the value to get the total value of each type of coin.
  • Step 4.  Translate into an equation. Write the equation by adding the total values of all the types of coins.
  • Step 5.  Solve the equation using good algebra techniques.
  • Step 6.  Check the answer in the problem and make sure it makes sense. 
  • Step 7.  Answer the question with a complete sentence.

 

Section Exercises

Use a Problem-solving Strategy for Word Problems

In the following exercises, use the problem-solving strategy for word problems to solve. Answer in complete sentences.

1. Two-thirds of the children in the fourth-grade class are girls. If there are [latex]20[/latex] girls, what is the total number of children in the class?

Show Solution

There are 30 children in the class.

 

 

2. Three-fifths of the members of the school choir are women. If there are [latex]24[/latex] women, what is the total number of choir members?

3. Zachary has [latex]25[/latex] country music CDs, which is one-fifth of his CD collection. How many CDs does Zachary have?

Show Solution

Zachary has 125 CDs.

4. One-fourth of the candies in a bag of are red. If there are [latex]23[/latex] red candies, how many candies are in the bag?

5. There are [latex]16[/latex]  girls in a school club. The number of girls is [latex]4[/latex] more than twice the number of boys. Find the number of boys in the club.  

Show Solution

There are 6 boys in the club.

 

6. There are [latex]18[/latex] Cub Scouts in Troop [latex]645[/latex]. The number of Scouts is [latex]3[/latex] more than five times the number of adult leaders. Find the number of adult leaders. 

7. Lee is emptying dishes and glasses from the dishwasher. The number of dishes is [latex]8[/latex] less than the number of glasses. If there are [latex]9[/latex] dishes, what is the number of glasses?

Show Solution

There are 17 glasses.

8. The number of puppies in the pet store window is twelve less than the number of dogs in the store. If there are [latex]6[/latex] puppies in the window, what is the number of dogs in the store?
9. After [latex]3[/latex] months on a diet, Lisa had lost [latex]12 \%[/latex] of her original weight. She lost [latex]21[/latex] pounds. What was Lisa’s original weight? 
Show Solution

Lisa’s original weight was 175 pounds.

 

10. Tricia got a [latex]6 \%[/latex] raise on her weekly salary. The raise was [latex]\% 30[/latex] per week. What was her original salary?

11. Tim left a [latex]\$ 9[/latex] tip for a [latex]\$ 50[/latex] restaurant bill. What percent tip did he leave?

Show Solution

[latex]18 \%[/latex]

12. Rashid left a [latex]\$ 15[/latex] tip for a [latex]\$ 75[/latex] restaurant bill. What percent tip did he leave?

13. Yuki bought a dress on sale for [latex]\$ 72[/latex]. The sale price was [latex]60 \%[/latex] of the original price. What was the original price of the dress?

Show Solution

The original price was $120.

 

14. Kim bought a pair of shoes on sale for [latex]\$ 40.50[/latex]. The sale price was [latex]45 \%[/latex] of the original price. What was the original price of the shoes?

Solve Number Problems

In the following exercises, solve each number word problem.

15. The sum of a number and eight is [latex]12[/latex]. Find the number.

Show Solution

[latex]4[/latex]

16. The sum of a number and nine is [latex]17[/latex]. Find the number.

17. The difference of a number and twelve is [latex]3[/latex]. Find the number. 

Show Solution

[latex]15[/latex]

18. The difference of a number and eight is [latex]4[/latex]. Find the number.

19. The sum of three times a number and eight is [latex]23[/latex]. Find the number.

Show Solution

[latex]5[/latex]

 

20. The sum of twice a number and six is [latex]14[/latex]. Find the number. 

21. The difference of twice a number and seven is [latex]17[/latex]. Find the number. 

Show Solution

[latex]12[/latex]

22. The difference of four times a number and seven is [latex]21[/latex]. Find the number. 

23. Three times the sum of a number and nine is [latex]12[/latex]. Find the number. 
Show Solution

[latex]-5[/latex]

24. Six times the sum of a number and eight is [latex]30[/latex]. Find the number.

25. One number is six more than the other. Their sum is forty-two. Find the numbers.

Show Solution

[latex]18, 24[/latex]

26. One number is five more than the other. Their sum is thirty-three. Find the numbers.

27. The sum of two numbers is twenty. One number is four less than the other. Find the numbers.

Show Solution

[latex]8, 12[/latex]

28. The sum of two numbers is twenty-seven. One number is seven less than the other. Find the numbers.

29. A number is one more than twice another number. Their sum is negative five. Find the numbers.

Show Solution

[latex]-2, -3[/latex]

30.One number is six more than five times another. Their sum is six. Find the numbers.

31. The sum of two numbers is fourteen. One number is two less than three times the other. Find the numbers.

Show Solution

[latex]4, 10[/latex]

32. The sum of two numbers is zero. One number is nine less than twice the other. Find the numbers.

33. One number is fourteen less than another. If their sum is increased by seven, the result is [latex]85[/latex]. Find the numbers. 

Show Solution

[latex]32, 46[/latex]

34. One number is eleven less than another. If their sum is increased by eight, the result is [latex]71[/latex]. Find the numbers. 

35. The sum of two consecutive integers is [latex]77[/latex]. Find the integers

.

Show Solution

[latex]38, 39[/latex]

36. The sum of two consecutive integers is [latex]89[/latex]. Find the integers. 

37. The sum of two consecutive integers is [latex]-23[/latex]. Find the integers. 

Show Solution

[latex]-11, -12[/latex]

38. The sum of two consecutive integers is [latex]-37[/latex]. Find the integers. 

39. The sum of three consecutive integers is [latex]78[/latex]. Find the integers. 

Show Solution

[latex]25, 26, 27[/latex]

40. The sum of three consecutive integers is [latex]60[/latex]. Find the integers. 

41. Find three consecutive integers whose sum is [latex]-36[/latex].

Show Solution

[latex]-11, -12, -13[/latex]

42. Find three consecutive integers whose sum is [latex]-3[/latex]

Everyday Math

43. Shopping Patty paid  $35 for a purse on sale for [latex]/$ 10[/latex] off the original price. What was the original price of the purse? 

Show Solution

The original price was $45.

44. Shopping Travis bought a pair of boots on sale for [latex]\$ 25[/latex] off the original price. He paid [latex]\$ 60[/latex] for the boots. What was the original price of the boots?

45. Shopping Minh spent [latex]\$6.25[/latex] on [latex]5[/latex] sticker books to give his nephews. Find the cost of each sticker book.

Show Solution

Each sticker book cost $1.25.

46. Shopping Alicia bought a package of [latex]8[/latex] peaches for [latex]\$ 3.20[/latex]. Find the cost of each peach. 

47. Shopping Tom paid [latex]\$ 1,166.40[/latex] for a new refrigerator, including [latex]\$ 86.40[/latex] tax. What was the price of the refrigerator before tax?

Show Solution

The price of the refrigerator before tax was $1,080.

48. Shopping Kenji paid [latex]\$ 2,279[/latex] for a new living room set, including [latex]\$ 129[/latex] tax. What was the price of the living room set before tax? 

Writing Exercises

49. Write a few sentences about your thoughts and opinions of word problems. Are these thoughts positive, negative, or neutral? If they are negative, how might you change your way of thinking in order to do better?

Show Solution

Answers will vary.

50. When you start to solve a word problem, how do you decide what to let the variable represent?

Verbal

  1. To set up a model linear equation to fit real-world applications, what should always be the first step?
Show Solution

Answers may vary. Possible answers: We should define in words what our variable is representing. We should declare the variable. A heading.

  1. Use your own words to describe this equation where n is a number:

[latex]5\left(n+3\right)=2n[/latex]

  1. If the total amount of money you had to invest was $2,000 and you deposit[latex]\,x\,[/latex]amount in one investment, how can you represent the remaining amount?
Show Solution

[latex]2,000-x[/latex]

  1. If a man sawed a 10-ft board into two sections and one section was[latex]\,n\,[/latex]ft long, how long would the other section be in terms of[latex]\,n[/latex]?
  1. If Bill was traveling[latex]\,v\,[/latex]mi/h, how would you represent Daemon’s speed if he was traveling 10 mi/h faster?
Show Solution

[latex]v+10[/latex]

Real-World Applications

For the following exercises, use the information to find a linear algebraic equation model to use to answer the question being asked.

  1. Mark and Don are planning to sell each of their marble collections at a garage sale. If Don has 1 more than 3 times the number of marbles Mark has, how many does each boy have to sell if the total number of marbles is 113?
  1. Beth and Ann are joking that their combined ages equal Sam’s age. If Beth is twice Ann’s age and Sam is 69 yr old, what are Beth and Ann’s ages?
Show Solution

Ann:[latex]\,23;[/latex] Beth:[latex]\,46[/latex]

  1. Ben originally filled out 8 more applications than Henry. Then each boy filled out 3 additional applications, bringing the total to 28. How many applications did each boy originally fill out?

For the following exercises, use this scenario: Two different telephone carriers offer the following plans that a person is considering. Company A has a monthly fee of $20 and charges of $.05/min for calls. Company B has a monthly fee of $5 and charges $.10/min for calls.

  1. Find the model of the total cost of Company A’s plan, using[latex]\,m\,[/latex]for the minutes.
Show Solution

[latex]20+0.05m[/latex]

  1. Find the model of the total cost of Company B’s plan, using[latex]\,m\,[/latex]for the minutes.
  1. Find out how many minutes of calling would make the two plans equal.
Show Solution

300 min

  1. If the person makes a monthly average of 200 min of calls, which plan should for the person choose?

For the following exercises, use this scenario: A wireless carrier offers the following plans that a person is considering. The Family Plan: $90 monthly fee, unlimited talk and text on up to 8 lines, and data charges of $40 for each device for up to 2 GB of data per device. The Mobile Share Plan: $120 monthly fee for up to 10 devices, unlimited talk and text for all the lines, and data charges of $35 for each device up to a shared total of 10 GB of data. Use[latex]\,P\,[/latex]for the number of devices that need data plans as part of their cost.

  1. Find the model of the total cost of the Family Plan.
Show Solution

[latex]90+40P[/latex]

  1. Find the model of the total cost of the Mobile Share Plan.
  1. Assuming they stay under their data limit, find the number of devices that would make the two plans equal in cost.
Show Solution

6 devices

  1. If a family has 3 smart phones, which plan should they choose?

For exercises 17 and 18, use this scenario: A retired woman has $50,000 to invest but needs to make $6,000 a year from the interest to meet certain living expenses. One bond investment pays 15% annual interest. The rest of it she wants to put in a CD that pays 7%.

  1. If we let[latex]\,x\,[/latex]be the amount the woman invests in the 15% bond, how much will she be able to invest in the CD?
Show Solution

[latex]50,000-x[/latex]

  1. Set up and solve the equation for how much the woman should invest in each option to sustain a $6,000 annual return.
  1. Two planes fly in opposite directions. One travels 450 mi/h and the other 550 mi/h. How long will it take before they are 4,000 mi apart?
Show Solution

4 h

  1. Ben starts walking along a path at 4 mi/h. One and a half hours after Ben leaves, his sister Amanda begins jogging along the same path at 6 mi/h. How long will it be before Amanda catches up to Ben?
  1. Fiora starts riding her bike at 20 mi/h. After a while, she slows down to 12 mi/h, and maintains that speed for the rest of the trip. The whole trip of 70 mi takes her 4.5 h. For what distance did she travel at 20 mi/h?
Show Solution

She traveled for 2 h at 20 mi/h, or 40 miles.

  1. A chemistry teacher needs to mix a 30% salt solution with a 70% salt solution to make 20 qt of a 40% salt solution. How many quarts of each solution should the teacher mix to get the desired result?
  1. Paul has $20,000 to invest. His intent is to earn 11% interest on his investment. He can invest part of his money at 8% interest and part at 12% interest. How much does Paul need to invest in each option to make get a total 11% return on his $20,000?
Show Solution

$5,000 at 8% and $15,000 at 12%

For the following exercises, use this scenario: A truck rental agency offers two kinds of plans. Plan A charges $75/wk plus $.10/mi driven. Plan B charges $100/wk plus $.05/mi driven.

  1. Write the model equation for the cost of renting a truck with plan A.
  1. Write the model equation for the cost of renting a truck with plan B.
Show Solution

[latex]B=100+.05x[/latex]

  1. Find the number of miles that would generate the same cost for both plans.
  1. If Tim knows he has to travel 300 mi, which plan should he choose?
Show Solution

Plan A

  1. For the following exercises, use the given formulas to answer the questions.
  1. [latex]A=P\left(1+rt\right)\,[/latex]is used to find the principal amount P deposited, earning r% interest, for t years. Use this to find what principal amount P David invested at a 3% rate for 20 yr if[latex]\,A=\text{\$}8,000.[/latex]
  1. The formula[latex]\,F=\frac{m{v}^{2}}{R}\,[/latex]relates force (F), velocity (v), mass (m), and resistance (R). Find[latex]\,R\,[/latex]when[latex]\,m=45,[/latex][latex]v=7,[/latex] and[latex]\,F=245.[/latex]
Show Solution

[latex]R=9[/latex]

  1. [latex]F=ma\,[/latex]indicates that force (F) equals mass (m) times acceleration (a). Find the acceleration of a mass of 50 kg if a force of 12 N is exerted on it.
  1. [latex]Sum=\frac{1}{1-r}\,[/latex]is the formula for an infinite series sum. If the sum is 5, find[latex]\,r.[/latex]
Show Solution

[latex]r=\frac{4}{5}\,[/latex]or 0.8

  1. For the following exercises, solve for the given variable in the formula. After obtaining a new version of the formula, you will use it to solve a question.
  1. Solve for W:[latex]\,P=2L+2W[/latex]
  1. Use the formula from the previous question to find the width,[latex]\,W,[/latex] of a rectangle whose length is 15 and whose perimeter is 58.
Show Solution

[latex]W=\frac{P-2L}{2}=\frac{58-2\left(15\right)}{2}=14[/latex]

  1. Solve for[latex]\,f:\frac{1}{p}+\frac{1}{q}=\frac{1}{f}[/latex]
  1. Use the formula from the previous question to find[latex]\,f\,[/latex]when[latex]\,p=8\,\text{and }q=13.[/latex]
Show Solution

[latex]f=\frac{pq}{p+q}=\frac{8\left(13\right)}{8+13}=\frac{104}{21}[/latex]

  1. Solve for[latex]\,m\,[/latex]in the slope-intercept formula:[latex]\,y=mx+b[/latex]
  1. Use the formula from the previous question to find[latex]\,m\,[/latex]when the coordinates of the point are[latex]\,\left(4,7\right)\,[/latex]and[latex]\,b=12.[/latex]
Show Solution

[latex]m=\frac{-5}{4}[/latex]

  1. The area of a trapezoid is given by[latex]\,A=\frac{1}{2}h\left({b}_{1}+{b}_{2}\right).\,[/latex]Use the formula to find the area of a trapezoid with[latex]\,h=6,\text{ }{b}_{1}=14,\text{ and }{b}_{2}=8.[/latex]
  1. Solve for h:[latex]\,A=\frac{1}{2}h\left({b}_{1}+{b}_{2}\right)[/latex]
Show Solution

[latex]h=\frac{2A}{{b}_{1}+{b}_{2}}[/latex]

  1. Use the formula from the previous question to find the height of a trapezoid with[latex]\,A=150,\text{ }{b}_{1}=19,\text{ and }{b}_{2}=11.[/latex]
  1. Find the dimensions of an American football field. The length is 200 ft more than the width, and the perimeter is 1,040 ft. Find the length and width. Use the perimeter formula[latex]\,P=2L+2W.[/latex]
Show Solution

length = 360 ft; width = 160 ft

  1. Distance equals rate times time,[latex]\,d=rt.\,[/latex]Find the distance Tom travels if he is moving at a rate of 55 mi/h for 3.5 h.
  1. Using the formula in the previous exercise, find the distance that Susan travels if she is moving at a rate of 60 mi/h for 6.75 h.
Show Solution

405 mi

  1. What is the total distance that two people travel in 3 h if one of them is riding a bike at 15 mi/h and the other is walking at 3 mi/h?
  1. If the area model for a triangle is[latex]\,A=\frac{1}{2}bh,[/latex] find the area of a triangle with a height of 16 in. and a base of 11 in.
Show Solution

[latex]A=88\text{ in}{.}^{2}[/latex]

  1. Solve for h:[latex]\,A=\frac{1}{2}bh[/latex]
  1. Use the formula from the previous question to find the height to the nearest tenth of a triangle with a base of 15 and an area of 215.
Show Solution

28.7

  1. The volume formula for a cylinder is[latex]\,V=\pi {r}^{2}h.\,[/latex]Using the symbol[latex]\,\pi \,[/latex]in your answer, find the volume of a cylinder with a radius,[latex]\,r,[/latex] of 4 cm and a height of 14 cm.
  1. Solve for h:[latex]\,V=\pi {r}^{2}h[/latex]
Show Solution

[latex]h=\frac{V}{\pi {r}^{2}}[/latex]

  1. Use the formula from the previous question to find the height of a cylinder with a radius of 8 and a volume of[latex]\,16\pi[/latex]

Solve for r:[latex]\,V=\pi {r}^{2}h[/latex]

Show Solution

[latex]r=\sqrt{\frac{V}{\pi h}}[/latex]

  1. Use the formula from the previous question to find the radius of a cylinder with a height of 36 and a volume of[latex]\,324\pi .[/latex]
  1. The formula for the circumference of a circle is[latex]\,C=2\pi r.\,[/latex]Find the circumference of a circle with a diameter of 12 in. (diameter = 2r). Use the symbol[latex]\,\pi \,[/latex]in your final answer.
Show Solution

[latex]C=12\pi[/latex]

  1. Solve the formula from the previous question for[latex]\,\pi .\,[/latex]Notice why[latex]\,\pi \,[/latex]is sometimes defined as the ratio of the circumference to its diameter.

Solve Coin Word Problems

In the following exercises, solve the coin word problems.

1. Jaime has $2.60 in dimes and nickels. The number of dimes is 14 more than the number of nickels. How many of each coin does he have?

Show Solution

2. Lee has $1.75 in dimes and nickels. The number of nickels is 11 more than the number of dimes. How many of each coin does he have?

3. Ngo has a collection of dimes and quarters with a total value of $3.50.  The number of dimes is 7 more than the number of quarters. How many of each coin does he have?

Show Solution

4. Connor has a collection of dimes and quarters with a total value of $6.30. The number of dimes is 14 more than the number of quarters. How many of each coin does he have?

5. Carolyn has $2.55 in her purse in nickels and dimes. The number of nickels is 9 less than three times the number of dimes. Find the number of each type of coin.

Show Solution

6. Julio has $2.75  in his pocket in nickels and dimes. The number of dimes is 10 less than twice the number of nickels. Find the number of each type of coin.

7. Chi has $11.30 in dimes and quarters. The number of dimes is 3 more than three times the number of quarters. How many dimes and nickels does Chi have?

Show Solution

8. Tyler has $9.70 in dimes and quarters. The number of quarters is 8 more than four times the number of dimes. How many of each coin does he have?

9. A cash box of $1 and $5 bills is worth $45. The number of $1 bills is 3 more than the number of $5 bills. How many of each bill does it contain?

Show Solution

10. Joe’s wallet contains $1 and $5 bills worth $47. The number of $1 bills is 5 more than the number of $5 bills. How many of each bill does he have?

11. In a cash drawer there is $125 in $5 and $10 bills. The number of $10 bills is twice the number of $5 bills. How many of each are in the drawer?

Show Solution

12. John has $175 in $5 and $10 bills in his drawer. The number of $5 bills is three times the number of $10 bills. How many of each are in the drawer?

13. Mukul has $3.75 in quarters, dimes and nickels in his pocket. He has five more dimes than quarters and nine more nickels than quarters. How many of each coin are in his pocket?

Show Solution

14. Vina has $4.70 in quarters, dimes and nickels in her purse. She has eight more dimes than quarters and six more nickels than quarters. How many of each coin are in her purse?

Solve Ticket and Stamp Word Problems

In the following exercises, solve the ticket and stamp word problems.

15. The play took in $550 one night. The number of $8 adult tickets was 10 less than twice the number of $5 child tickets. How many of each ticket were sold?

Show Solution

16. If the number of $8 child tickets is seventeen less than three times the number of $12 adult tickets and the theater took in $584, how many of each ticket were sold?

17. The movie theater took in $1,220 one Monday night. The number of $7 child tickets was ten more than twice the number of $9 adult tickets. How many of each were sold?

Show Solution

18. The ball game took in $1,340 one Saturday. The number of $12 adult tickets was 15 more than twice the number of $5 child tickets. How many of each were sold?

19. Julie went to the post office and bought both $0.49 stamps and $0.34 postcards for her office’s bills She spent $62.60. The number of stamps was 20 more than twice the number of postcards. How many of each did she buy?

Show Solution

20. Before he left for college out of state, Jason went to the post office and bought both $0.49 stamps and $0.34 postcards and spent $12.52. The number of stamps was 4 more than twice the number of postcards. How many of each did he buy?

21. Maria spent $16.80 at the post office. She bought three times as many $0.49 stamps as $0.21 stamps. How many of each did she buy?

Show Solution

22. Hector spent $43.40 at the post office. He bought four times as many $0.49 stamps as $0.21 stamps. How many of each did he buy?

23. Hilda has $210 worth of $10 and $12 stock shares. The numbers of $10 shares is 5 more than twice the number of $12 shares. How many of each does she have?

Show Solution

24. Mario invested $475 in $45 and $25 stock shares. The number of $25 shares was 5 less than three times the number of $45 shares. How many of each type of share did he buy?

Everyday Math

25. Parent Volunteer As the treasurer of her daughter’s Girl Scout troop, Laney collected money for some girls and adults to go to a 3-day camp. Each girl paid $75 and each adult paid $30. The total amount of money collected for camp was $765. If the number of girls is three times the number of adults, how many girls and how many adults paid for camp?

Show Solution

26. Parent Volunteer Laurie was completing the treasurer’s report for her son’s Boy Scout troop at the end of the school year. She didn’t remember how many boys had paid the $24 full-year registration fee and how many had paid a $16 partial-year fee. She knew that the number of boys who paid for a full-year was ten more than the number who paid for a partial-year. If $400 was collected for all the registrations, how many boys had paid the full-year fee and how many had paid the partial-year fee?

Writing Exercises

27. Suppose you have 6 quarters, 9 dimes, and 4 pennies. Explain how you find the total value of all the coins.

28. Do you find it helpful to use a table when solving coin problems? Why or why not?

29. In the table used to solve coin problems, one column is labeled “number” and another column is labeled ‘“value.” What is the difference between the number and the value?

30. What similarities and differences did you see between solving the coin problems and the ticket and stamp problems?

Glossary

area
in square units, the area formula used in this section is used to find the area of any two-dimensional rectangular region:[latex]\,A=LW[/latex]
perimeter
in linear units, the perimeter formula is used to find the linear measurement, or outside length and width, around a two-dimensional regular object; for a rectangle:[latex]\,P=2L+2W[/latex]
volume
in cubic units, the volume measurement includes length, width, and depth:[latex]\,V=LWH[/latex]

Media Attributions

License

Icon for the Creative Commons Attribution 4.0 International License

2.2 Models and Applications Copyright © by Cynthia Singleton; Ginny Bradley; Karen Perilloux; and Prakash Ghimire is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book