5.7 Variation
Karen Perilloux; Prakash Ghimire; and Lauren Johnson
Learning Objectives
By the end of this section, you will be able to:
- Solve direct variation problems.
- Solve inverse variation problems.
- Solve problems involving joint variation.
- Relating Pressure, Volume, Amount, and Temperature: The Ideal Gas Law
Solve a formula for a specific variable.
It is often helpful to solve a formula for a specific variable. If you need to put a formula in a spreadsheet, it is not unusual to have to solve it for a specific variable first. We isolate that variable on one side of the equals sign, and all other variables and constants are on the other side of the equal sign.
Example
Solve the formula [latex]V =\frac{1}{3} \pi r^2 h[/latex] for h
Show Solution
| Write the formula. | [latex]V = \frac{1}{3} \pi r^2 h[/latex] |
| Remove the fraction on the right. | [latex]3 \times V = 3 times frac{1}{3} \pi r^2 h[/latex] |
| Simplify. | [latex]3 V = \pi r^2 h[/latex] |
| Divide both sides by | [latex]\frac{3V}{pi r^2} = h[/latex] |
We could now use this formula to find the height of a right circular cone when we know the volume and the radius of the base, by using the formula
Solve direct variation problems
When two quantities are related by a proportion, we say they are proportional to each other. Another way to express this relation is to talk about the variation of the two quantities. We will discuss direct variation and inverse variation in this section.
Lindsay gets paid \( \$ 15 \) per hour at her job. If we let \( S \) be her salary and h be the number of hours she has worked, we could model this situation with the equation \( S = 15 h \).
Lindsay’s salary is the product of a constant, 15, and the number of hours she works. We say that Lindsay’s salary varies directly with the number of hours she works. Two variables vary directly if one is the product of a constant and the other.
Which graph represents direct variation and why?
ⓐ
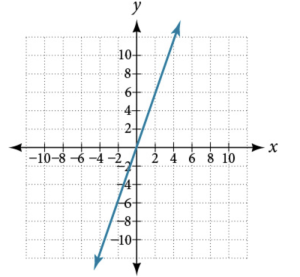
ⓑ
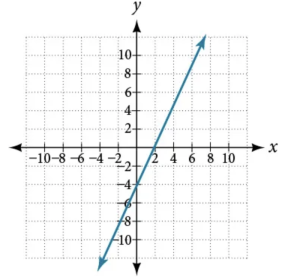
Direct Variation
For any two variables \( x \) and \( y \), \( y \) varies directly with \( x \) if
\( y = k x , \ \ \text{where} \ k \neq 0 \)
The constant \( k \) is called the constant of variation.
How To
Solve direct variation problems.
- Step 1. Write the formula for direct variation.
- Step 2. Substitute the given values for the variables.
- Step 3. Solve for the constant of variation.
- Step 4. Write the equation that relates x and y using the constant of variation.
Example
When Raoul runs on the treadmill at the gym, the number of calories, c, he burns varies directly with the number of minutes, m, he uses the treadmill. He burned 315 calories when he used the treadmill for 18 minutes.
ⓐ Write the equation that relates c and m. ⓑ How many calories would he burn if he ran on the treadmill for 25 minutes?
Show Solution
ⓐ The number of calories, c, varies directly with the number of minutes, m, on the treadmill, and \( c = 315 \) when \( m =18 \).
| Write the formula for direct variation. | y = kx |
| We will use c in place of y and m in place of x. | c= km |
| Substitute the given values for the variables. | 315 = k . 18 |
| Solve for the constant of variation. | \( \frac{315}{18} = \frac{k \cdot 18 }{18} \) \( 17.5 = k \) |
| Write the equation that relates c and m. | \( c = k m \) |
| Substitute in the constant of variation. | \( c = 17.5 m \) |
ⓑ Find c when m = 25.
| Write the equation that relates c and m. | \( c = 17.5 m \) |
| Substitute the given value for m. | \( c = 17.5 ( 25) \) |
| Simplify. | \( c = 437.5 \) |
| Raoul would burn 437.5 calories if he used the treadmill for 25 minutes. |
Solving Direct Variation Problems
A pre-owned car dealer has just offered their best candidate, Nicole, a position in sales. The position offers 16% commission on her sales. Her earnings depend on the amount of her sales. For instance, if she sells a vehicle for $4,600, she will earn $736. As she considers the offer, she takes into account the typical price of the dealer’s cars, the overall market, and how many she can reasonably expect to sell. In this section, we will look at relationships, such as this one, between earnings, sales, and commission rate.
In the example above, Nicole’s earnings can be found by multiplying her sales by her commission. The formula \( e = 0.16s \) tells us her earnings \( e \), come from the product of \( 0.16 \), her commission, and the sale price of the vehicle. If we create a table, we observe that as the sales price increases, the earnings increase as well, which should be intuitive. See Table below:
| s, sales price | Interpretation | |
|---|---|---|
| $4,600 | A sale of a $4,600 vehicle results in $736 earnings. | |
| $9,200 | A sale of a $9,200 vehicle results in $1472 earnings. | |
| $18,400 | A sale of a $18,400 vehicle results in $2944 earnings. |
Notice that earnings are a multiple of sales. As sales increase, earnings increase in a predictable way. Double the sales of the vehicle from $4,600 to $9,200, and we double the earnings from $736 to $1,472. As the input increases, the output increases as a multiple of the input. A relationship in which one quantity is a constant multiplied by another quantity is called direct variation. Each variable in this type of relationship varies directly with the other.
The Figure below represents the data for Nicole’s potential earnings. We say that earnings vary directly with the sales price of the car. The formula \( y = k x^n \) is used for direct variation. The value of \( k \) is a nonzero constant greater than zero and is called the constant of variation. In this case, \( k = 0.16 \) and \( n =1 \). We saw functions like this one when we discussed power functions.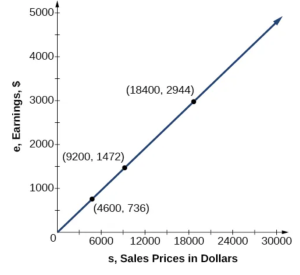
Direct Variation
If \( x \) and \( y \) are related by an equation of the form
\( y = k x^n \)
then we say that the relationship is direct variation, and \( y \) varies directly with or is proportional to, the n the power of \( x \). In direct variation relationships, there is a non zero constant ratio \( k = \frac{y}{x^n} \), where \( k \) is called the constant of variation, which help defines the relationship between the variables.
How To
Given a description of a direct variation problem, solve for an unknown.
- Identify the input, \( x \), and the output, \( y \).
- Determine the constant of variation. You may need to divide \( y \) by the specified power of \( x \) to determine the constant of variation.
- Use the constant of variation to write an equation for the relationship.
- Substitute known values into the equation to find the unknown.
Example
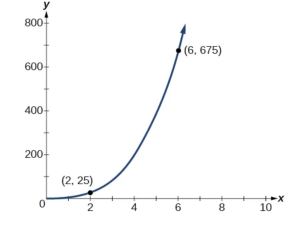
The quantity y varies directly with the cube of \( x \). If \( y = 25 \) when \( x = 2 \), find \( y \) when \( x \) is \( 6 \).
Show Solution
The general formula for direct variation with a cube is \( y = k x^3 \). The constant can be found by dividing \( y \) by the cube of \( x \).
Now use the constant to write an equation that represents this relationship.
Substitute \( x = 6 \) and solve for \( y \).
Analysis
The graph of this equation is a simple cubic, as shown in Figure below.
Q & A
Do the graphs of all direct variation equations look like the Example above?
No. Direct variation equations are power functions—they may be linear, quadratic, cubic, quartic, radical, etc. But all of the graphs pass through (0, 0).
Try It
The quantity \( y \) varies directly with the square of \( x \). If \( y = 24 \) when \( x = 3 \), find \( y \) when \( x \) is \( 4 \).
Show Solution
[latex]\frac{128}{3}[/latex]
Access the online resource below for additional instruction and practice with direct variation problems:
Solving Inverse Variation Problems
Water temperature in an ocean varies inversely to the water’s depth. The formula \( T = \frac{14,000}{d} \) gives us the temperature in degrees Fahrenheit at a depth in feet below Earth’s surface. Consider the Atlantic Ocean, which covers 22% of Earth’s surface. At a certain location, at the depth of 500 feet, the temperature may be 28°F.
If we create Table below, we observe that, as the depth increases, the water temperature decreases.
| depth | Interpretation | |
|---|---|---|
| 500 ft | At a depth of 500 ft, the water temperature is 28° F. | |
| 1000 ft | At a depth of 1,000 ft, the water temperature is 14° F. | |
| 2000 ft | At a depth of 2,000 ft, the water temperature is 7° F. |
We notice in the relationship between these variables that, as one quantity increases, the other decreases. The two quantities are said to be inversely proportional and each term varies inversely with the other. Inversely proportional relationships are also called inverse variations.
For our example, the Figure below depicts the inverse variation. We say the water temperature varies inversely with the depth of the water because, as the depth increases, the temperature decreases. The formula \( y = \frac{k}{x} \) for inverse variation in this case uses \( k = 14,000 \).
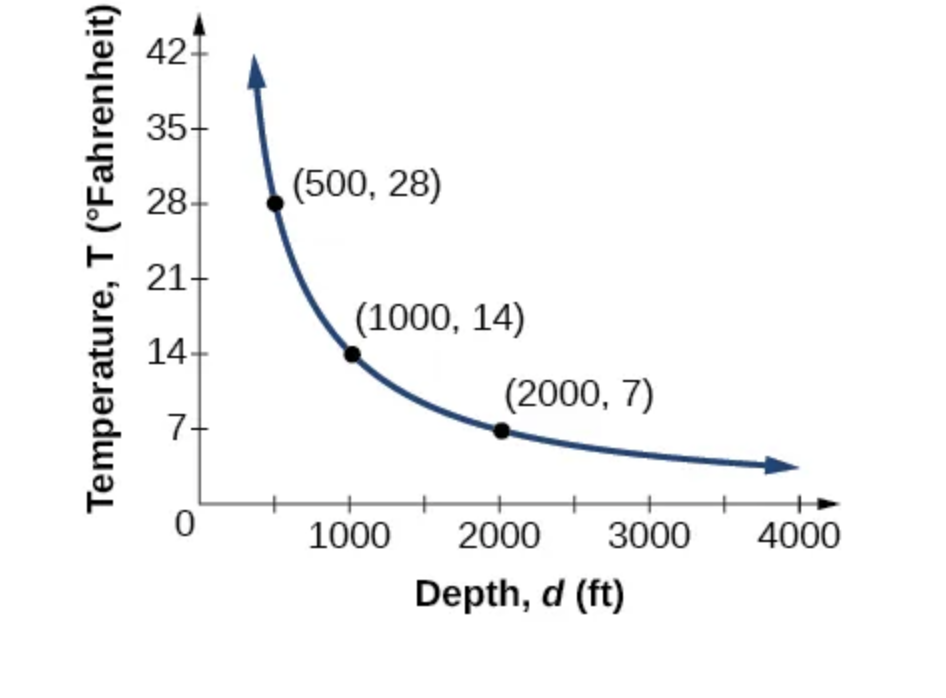
Inverse Variation
If \( x \) and \( y \) are related by an equation of the form
\( y = \frac{k}{x^n} \)
where \( k \) is a nonzero constant, then we say that \( y \) varies inversely with nth power of \( x \). In inversely proportional relationships, or inverse variations, there is a constant multiple \( k = x^n y \).
Example
A tourist plans to drive 100 miles. Find a formula for the time the trip will take as a function of the speed the tourist drives.
Show Solution
Recall that multiplying speed by time gives the distance. If we let \( t \) represent the drive time in hours and \( v \) represent the velocity ( speed or rate) at which the tourist drives, that \( vt = \text{distance} \). Because the distance is fixed at \( 100 \) miles. \( vt = 100\) so \( t = \frac{100}{v} \). Because time is a function of velocity, we can write \( t(v) \).
\( t(v) = \frac{100}{v} \)
\( = 100v^{-1} \)
We can see that the constant of variation is 100 and, although we can write the relationship using the negative exponent, it is more common to see it written as a fraction. We say that time varies inversely with velocity.
How To
Given a description of an indirect variation problem, solve for an unknown.
- Identify the input, \( x \), and the output \( y \).
- Determine the constant of variation. You may need to multiply \( y \) by the specified power of \( x \) to determine the constant of variation.
- Use the constant of variation to write an equation for the relationship.
- Substitute known values into the equation to find the unknown.
Example
A quantity \( y \) varies inversely with the cube of \( x \). If \( y = 25 \) when \( x = 2\), find \( y \) when \( 9 x \) is \( 6 \).
Show Solution
The general formula for inverse variation with a cube is \( y = \frac{k}{x^3} \). The constant can be found by multiplying \( y \) by the cube of \( x \).
Now we use the constant to write an equation that represents this relationship.
Substitute \( x = 6 \) and solve for \( y \)
Analysis
The graph of this equation is a rational function, as shown in Figure below.
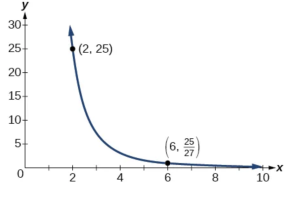
Try It
A quantity \( y \) varies inversely with the square of \( x \). If \( y = 8 \) when \( x = 3 \), find \( y \) when \( x \) is \( 4 \).
Show Solution
[latex]\frac{9}{2}[/latex]
Access the online resource below for additional instruction and practice with inverse variation problems:
Solving Problems Involving Joint Variation
Many situations are more complicated than a basic direct variation or inverse variation model. One variable often depends on multiple other variables. When a variable is dependent on the product or quotient of two or more variables, this is called joint variation. For example, the cost of busing students for each school trip varies with the number of students attending and the distance from the school. The variable \( c \), cost, varies jointly with the number of students, \( n \), and the distance, \( d \).
Joint Variation
Joint variation occurs when a variable varies directly or inversely with multiple variables. For instance, if \( x \) varies directly with both \( y \) and \( z \), we have \( x = k y z \). If \( x \) varies directly with \( y \) and inversely with \( z \), we have \( x = \frac{ky}{z} \). Notice that we only use one constant in a joint variation equation.
Example
If \( x = 6 \) when \( y = 2 \) and \( z = 8\), find \( x \) when \( y =1 \) and \( z = 27 \).
Show Solution
Begin by writing an equation to show the relationship between the variables.
Substitute \( x = 6 \), \( y = 2 \), and \( z = 8 \) to find the value of the constant \( k \).
Now we can substitute the value of the constant into the equation for the relationship.
To find \( x \) when \( y =1 \) and \( z = 27 \), we will substitute values for \( y \) and \( z \) into our equation.
Try It
A quantity \( x \) varies directly with the square of \( y \) and inversely with \( z \). If \( x = 40 \) when \( y = 4 \) and \( z = 2 \), find \( x \) when \( y= 10 \) and \( z = 25 \).
Show Solution
[latex] 20 [/latex]
Access the online resource below for additional instruction and practice with joint variation problems:
Relating Pressure, Volume, Amount, and Temperature: The Ideal Gas Law
During the seventeenth and especially eighteenth centuries, driven both by a desire to understand nature and a quest to make balloons in which they could fly (Figure 8.9), a number of scientists established the relationships between the macroscopic physical properties of gases, that is, pressure, volume, temperature, and amount of gas. Although their measurements were not precise by today’s standards, they were able to determine the mathematical relationships between pairs of these variables (e.g., pressure and temperature, pressure and volume) that hold for an ideal gas—a hypothetical construct that real gases approximate under certain conditions. Eventually, these individual laws were combined into a single equation—the ideal gas law—that relates gas quantities for gases and is quite accurate for low pressures and moderate temperatures. We will consider the key developments in individual relationships (for pedagogical reasons not quite in historical order), then put them together in the ideal gas law.

Pressure and Temperature: Amontons’s Law
Imagine filling a rigid container attached to a pressure gauge with gas and then sealing the container so that no gas may escape. If the container is cooled, the gas inside likewise gets colder and its pressure is observed to decrease. Since the container is rigid and tightly sealed, both the volume and number of moles of gas remain constant. If we heat the sphere, the gas inside gets hotter(Figure 8) and the pressure increases.
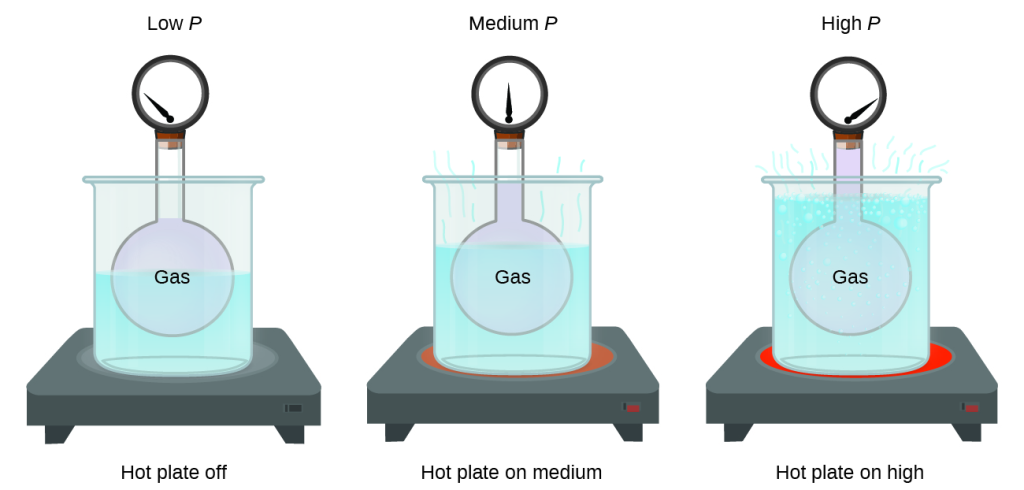
where ∝ means “is proportional to,” and k is a proportionality constant that depends on the identity, amount, and volume of the gas.
For a confined, constant volume of gas, the ratio [latex]\frac{P}{T}[/latex] is therefore constant (i.e.,[latex]\frac{P}{T}[/latex] = k). If the gas is initially in “Condition 1” (with P =P1 and T =T1), and then changes to “Condition 2” (with P = P2 and T = T2), we have that[latex]\frac{P _1}{T_1}[/latex] = k and [latex]\frac{P_2}{T_2}[/latex] = k, which reduces to [latex]\frac{P _1}{T_1}[/latex] = [latex]\frac{P_2}{T_2}[/latex]. This equation is useful for pressure-temperature calculations for a confined gas at constant volume. Note that temperatures must be on the kelvin scale for any gas law calculations (0 on the kelvin scale and the lowest possible temperature is called absolute zero). (Also note that there are at least three ways we can describe how the pressure of a gas changes as its temperature changes: We can use a table of values, a graph, or a mathematical equation.)
Example
A can of hair spray is used until it is empty except for the propellant, isobutane gas.
(a) On the can is the warning “Store only at temperatures below 120 °F (48.8 °C). Do not incinerate.” Why?
(b) The gas in the can is initially at 24 °C and 360 kPa, and the can has a volume of 350 mL. If the can is left in a car that reaches 50 °C on a hot day, what is the new pressure in the can?
Show Solution to a
Solution
(a) The can contains an amount of isobutane gas at a constant volume, so if the temperature is increased by heating, the pressure will increase proportionately. High temperature could lead to high pressure, causing the can to burst. (Also, isobutane is combustible, so incineration could cause the can to explode.)
Show Solution to b
Solution
(b) We are looking for a pressure change due to a temperature change at constant volume, so we will use Amontons’s/Gay-Lussac’s law. Taking P1 and T1 as the initial values, T2 as the temperature where the pressure is unknown and P2 as the unknown pressure, and converting °C to K, we have:
Rearranging and solving gives:
Try It
A sample of nitrogen, N2, occupies 45.0 mL at 27 °C and 600 torr. What pressure will it have if cooled to –73 °C while the volume remains constant?
Show Solution
400 torr
Volume and Temperature: Charles’s Law
If we fill a balloon with air and seal it, the balloon contains a specific amount of air at atmospheric pressure, let’s say 1 atm. If we put the balloon in a refrigerator, the gas inside gets cold and the balloon shrinks (although both the amount of gas and its pressure remain constant). If we make the balloon very cold, it will shrink a great deal, and it expands again when it warms up.
Link To Learning
This video shows how cooling and heating a gas causes its volume to decrease or increase, respectively.
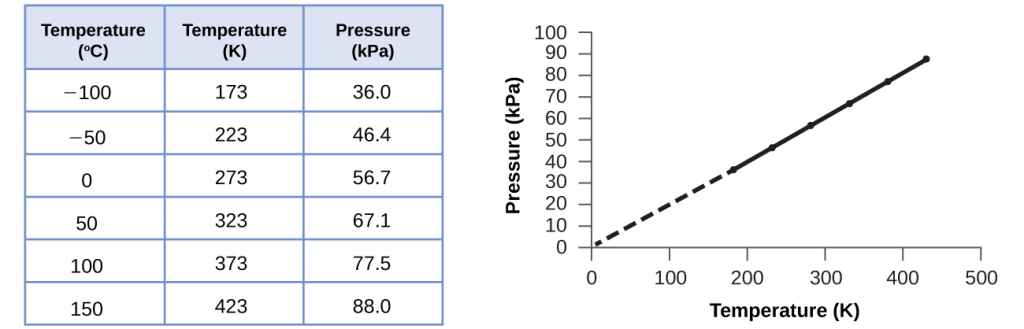
These examples of the effect of temperature on the volume of a given amount of a confined gas at constant pressure are true in general: The volume increases as the temperature increases, and decreases as the temperature decreases. Volume-temperature data for a 1-mole sample of methane gas at 1 atm are listed and graphed in Figure 10.
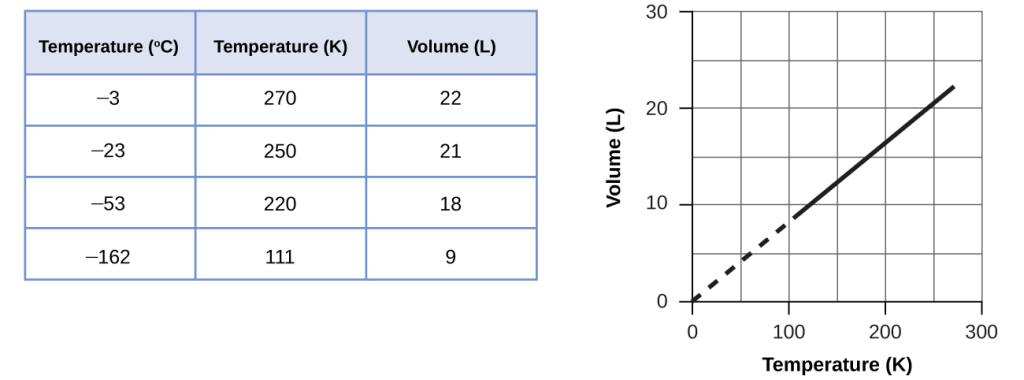
Mathematically, this can be written as:
with k being a proportionality constant that depends on the amount and pressure of the gas.
For a confined, constant pressure gas sample, [latex]\frac{V}{T}[/latex] is constant (i.e., the ratio = k), and as seen with the P–T relationship, this leads to another form of Charles’s law:
[latex]\frac{V_1}{T_1}[/latex] = [latex]\frac{V_2}{T_2}[/latex]
Example
Predicting Change in Volume with Temperature
A sample of carbon dioxide, CO2, occupies 0.300 L at 10 °C and 750 torr. What volume will the gas have at 30 °C and 750 torr?
Show Solution
Solution
| Because we are looking for the volume change caused by a temperature change at constant pressure, this is a job for Charles’s law. Taking V1 and T1 as the initial values, T2 as the temperature at which the volume is unknown and V2 as the unknown volume, and converting °C into K we have:
Rearranging and solving gives:
This answer supports our expectation from Charles’s law, namely, that raising the gas temperature (from 283 K to 303 K) at a constant pressure will yield an increase in its volume (from 0.300 L to 0.321 L).
|
Try It
A sample of oxygen, O2, occupies 32.2 mL at 30 °C and 452 torr. What volume will it occupy at –70 °C and the same pressure?
Show Solution
21.6 mL
Example
Measuring Temperature with a Volume Change
Temperature is sometimes measured with a gas thermometer by observing the change in the volume of the gas as the temperature changes at constant pressure. The hydrogen in a particular hydrogen gas thermometer has a volume of 150.0 cm3 when immersed in a mixture of ice and water (0.00 °C). When immersed in boiling liquid ammonia, the volume of the hydrogen, at the same pressure, is 131.7 cm3. Find the temperature of boiling ammonia on the kelvin and Celsius scales.
Show Solution
Rearrangement gives
Subtracting 273.15 from 239.8 K, we find that the temperature of the boiling ammonia on the Celsius scale is –33.4 °C.
Try It
What is the volume of a sample of ethane at 467 K and 1.1 atm if it occupies 405 mL at 298 K and 1.1 atm?
Show Solution
635 mL
Volume and Pressure: Boyle’s Law
If we partially fill an airtight syringe with air, the syringe contains a specific amount of air at constant temperature, say 25 °C. If we slowly push in the plunger while keeping temperature constant, the gas in the syringe is compressed into a smaller volume and its pressure increases; if we pull out the plunger, the volume increases and the pressure decreases. This example of the effect of volume on the pressure of a given amount of a confined gas is true in general. Decreasing the volume of a contained gas will increase its pressure, and increasing its volume will decrease its pressure. In fact, if the volume increases by a certain factor, the pressure decreases by the same factor, and vice versa. Volume-pressure data for an air sample at room temperature are graphed in Figure 11.
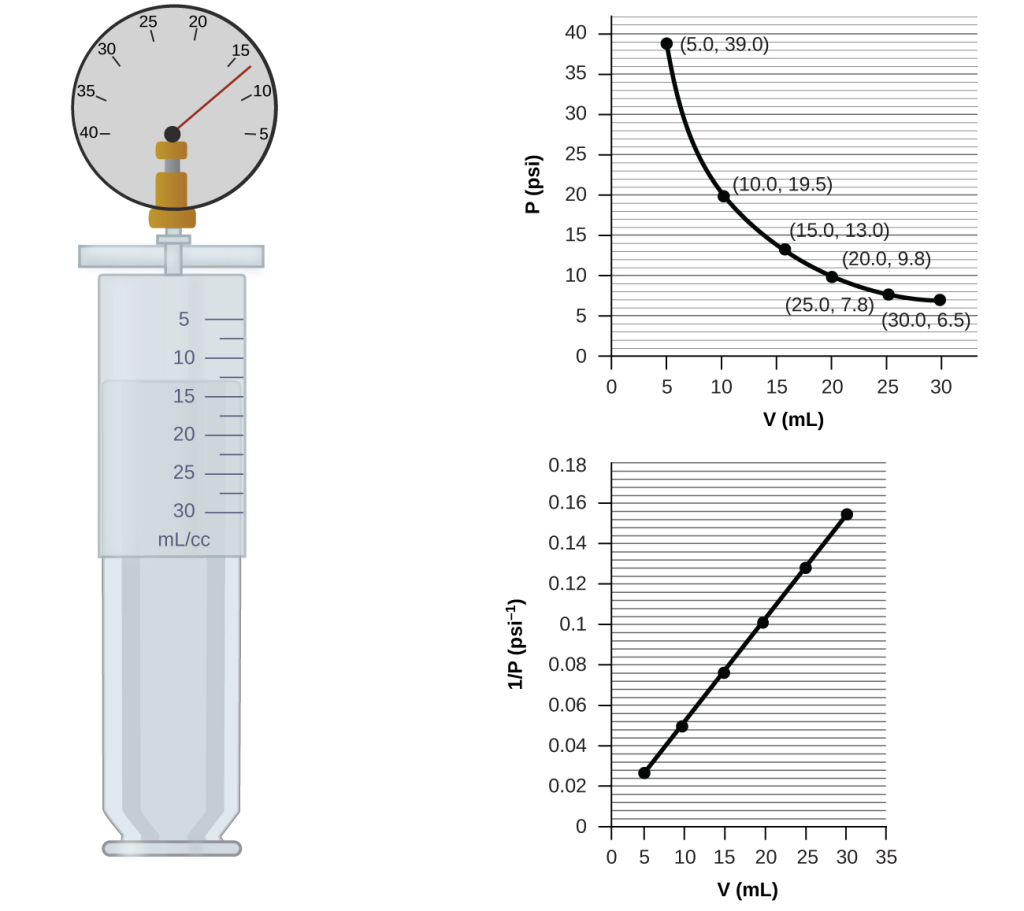
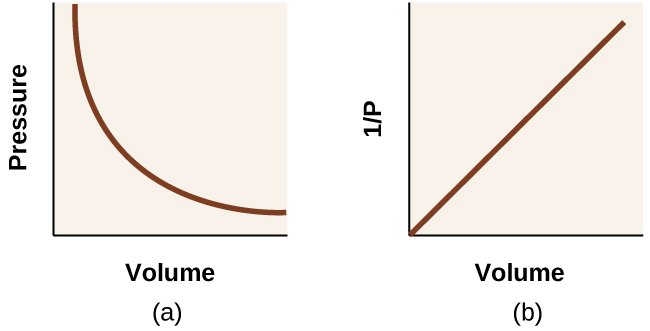
Unlike the P–T and V–T relationships, pressure and volume are not directly proportional to each other. Instead, P and V exhibit inverse proportionality: Increasing the pressure results in a decrease of the volume of the gas. Mathematically this can be written:
with k being a constant. Graphically, this relationship is shown by the straight line that results when plotting the inverse of the pressure [latex]{1}{P}[/latex] versus the volume (V), or the inverse of volume [latex]{1}{V}[/latex]versus the pressure (P). Graphs with curved lines are difficult to read accurately at low or high values of the variables, and they are more difficult to use in fitting theoretical equations and parameters to experimental data. For those reasons, scientists often try to find a way to “linearize” their data. If we plot P versus V, we obtain a hyperbola (see Figure 12).
Example
Volume of a Gas Sample
The sample of gas in Figure 11 has a volume of 15.0 mL at a pressure of 13.0 psi. Determine the pressure of the gas at a volume of 7.5 mL, using:
(a) the P-V graph in Figure 11
(b) the [latex]{1}{P}[/latex] vs. V graph in Figure 11
(c) the Boyle’s law equation
Comment on the likely accuracy of each method.
Show Solution to a
Solution
(a) Estimating from the P-V graph gives a value for P somewhere around 27 psi.
Show Solution to b
Solution
(b) Estimating from the[latex]{1}{P}[/latex]versus V graph give a value of about 26 psi.
Show Solution to c
Solution
(c) From Boyle’s law, we know that the product of pressure and volume (PV) for a given sample of gas at a constant temperature is always equal to the same value. Therefore we have P1V1 = k and P2V2 = k which means that P1V1 = P2V2.
Using P1 and V1 as the known values 13.0 psi and 15.0 mL, P2 as the pressure at which the volume is unknown, and V2 as the unknown volume, we have:
Solving:
It was more difficult to estimate well from the P-V graph, so (a) is likely more inaccurate than (b) or (c). The calculation will be as accurate as the equation and measurements allow.
Try It
The sample of gas in Figure 8.13 has a volume of 30.0 mL at a pressure of 6.5 psi. Determine the volume of the gas at a pressure of 11.0 psi, using:
(a) the P-V graph in Figure 8.13
(b) the[latex]{1}{P}[/latex]vs. V graph in Figure 8.13
(c) the Boyle’s law equation
Comment on the likely accuracy of each method.
Show Solution
(a) about 17–18 mL; (b) ~18 mL; (c) 17.7 mL; it was more difficult to estimate well from the P-V graph, so (a) is likely more inaccurate than (b); the calculation will be as accurate as the equation and measurements allow.
Chemistry in Everyday Life
Breathing and Boyle’s Law
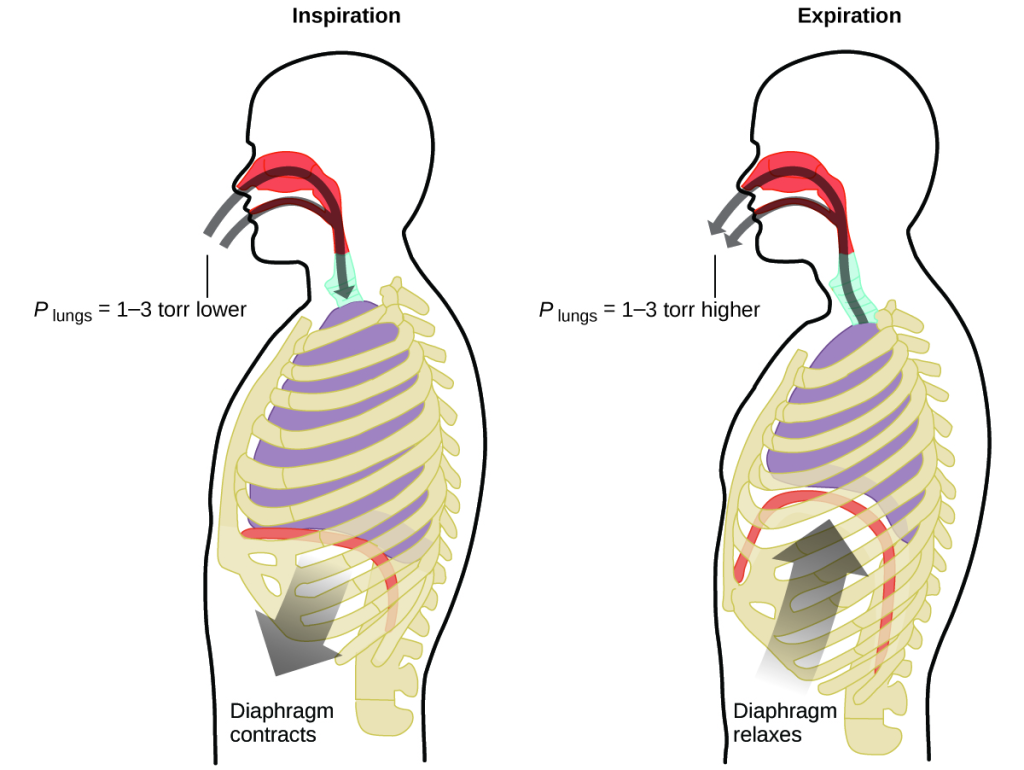
What do you do about 20 times per minute for your whole life, without break, and often without even being aware of it? The answer, of course, is respiration, or breathing. How does it work? It turns out that the gas laws apply here. Your lungs take in gas that your body needs (oxygen) and get rid of waste gas (carbon dioxide). Lungs are made of spongy, stretchy tissue that expands and contracts while you breathe. When you inhale, your diaphragm and intercostal muscles (the muscles between your ribs) contract, expanding your chest cavity and making your lung volume larger. The increase in volume leads to a decrease in pressure (Boyle’s law). This causes air to flow into the lungs (from high pressure to low pressure). When you exhale, the process reverses: Your diaphragm and rib muscles relax, your chest cavity contracts, and your lung volume decreases, causing the pressure to increase (Boyle’s law again), and air flows out of the lungs (from high pressure to low pressure). You then breathe in and out again, and again, repeating this Boyle’s law cycle for the rest of your life (Figure 8.15).
Moles of Gas and Volume: Avogadro’s Law
The Italian scientist Amedeo Avogadro advanced a hypothesis in 1811 to account for the behavior of gases, stating that equal volumes of all gases, measured under the same conditions of temperature and pressure, contain the same number of molecules. Over time, this relationship was supported by many experimental observations as expressed by Avogadro’s law: For a confined gas, the volume (V) and number of moles (n) are directly proportional if the pressure and temperature both remain constant.
In equation form, this is written as:
Mathematical relationships can also be determined for the other variable pairs, such as P versus n, and n versus T.
Link to learning
Visit this interactive PhET simulation to investigate the relationships between pressure, volume, temperature, and amount of gas. Use the simulation to examine the effect of changing one parameter on another while holding the other parameters constant (as described in the preceding sections on the various gas laws).
The Ideal Gas Law
To this point, four separate laws have been discussed that relate pressure, volume, temperature, and the number of moles of the gas:
- Boyle’s law: PV = constant at constant T and n
- Amontons's law: [latex]{P}{T}[/latex] = constant at constant V and n
- Charle's law:[latex]{V}{T}[/latex] = constant at constant P and n
- Avogadro's law: [latex]{V}{n}[/latex] = constant at constant P and T
Combining these four laws yields the ideal gas law, a relation between the pressure, volume, temperature, and number of moles of a gas:
where P is the pressure of a gas, V is its volume, n is the number of moles of the gas, T is its temperature on the kelvin scale, and R is a constant called the ideal gas constant or the universal gas constant. The units used to express pressure, volume, and temperature will determine the proper form of the gas constant as required by dimensional analysis, the most commonly encountered values being 0.08206 L atm mol–1 K–1 and 8.314 kPa L mol–1 K–1.
Gases whose properties of P, V, and T are accurately described by the ideal gas law (or the other gas laws) are said to exhibit ideal behavior or to approximate the traits of an ideal gas. An ideal gas is a hypothetical construct that may be used along with kinetic molecular theory to effectively explain the gas laws as will be described in a later module of this chapter. Although all the calculations presented in this module assume ideal behavior, this assumption is only reasonable for gases under conditions of relatively low pressure and high temperature. In the final module of this chapter, a modified gas law will be introduced that accounts for the non-ideal behavior observed for many gases at relatively high pressures and low temperatures.
The ideal gas equation contains five terms, the gas constant R and the variable properties P, V, n, and T. Specifying any four of these terms will permit use of the ideal gas law to calculate the fifth term as demonstrated in the following example exercises.
Example
When filled with air, a typical scuba tank with a volume of 13.2 L has a pressure of 153 atm
Show Solution
Solution
We must rearrange PV = nRT to solve for V = [latex]{nRT}{P}[/latex]
If we choose to use R = 0.08206 L atm mol–1 K–1, then the amount must be in moles, temperature must be in kelvin, and pressure must be in atm.
Converting into the “right” units:
It would require 1020 L (269 gal) of gaseous methane at about 1 atm of pressure to replace 1 gal of gasoline. It requires a large container to hold enough methane at 1 atm to replace several gallons of gasoline.
Try It
Calculate the pressure in bar of 2520 moles of hydrogen gas stored at 27 °C in the 180-L storage tank of a modern hydrogen-powered car.
Show Solution
350 bar
If the number of moles of an ideal gas are kept constant under two different sets of conditions, a useful mathematical relationship called the combined gas law is obtained:
using units of atm, L and K. Both sets of conditions are equal to the product of n x R (where n = the number of moles of the gas and R is the ideal gas law constant.
Example
Using the Combined Gas Law
When filled with air, a typical scuba tank with a volume of 13.2 L has a pressure of 153 atm (Figure 14). If the water temperature is 27 °C, how many liters of air will such a tank provide to a diver’s lungs at a depth of approximately 70 feet in the ocean where the pressure is 3.13 atm?

Show Solution
Solution
Letting 1 represent the air in the scuba tank and 2 represent the air in the lungs, and noting that body temperature (the temperature the air will be in the lungs) is 37 °C, we have:
Solving for V2:
(Note: Be advised that this particular example is one in which the assumption of ideal gas behavior is not very reasonable, since it involves gases at relatively high pressures and low temperatures. Despite this limitation, the calculated volume can be viewed as a good “ballpark” estimate.)
Try It
A sample of ammonia is found to occupy 0.250 L under laboratory conditions of 27 °C and 0.850 atm. Find the volume of this sample at 0 °C and 1.00 atm.
Show Solution
0.193 L
Chemistry in Everyday Life
The Interdependence between Ocean Depth and Pressure in Scuba Diving
Whether scuba diving at the Great Barrier Reef in Australia (shown in Figure 15) or in the Caribbean, divers must understand how pressure affects a number of issues related to their comfort and safety.

Standard Conditions of Temperature and Pressure
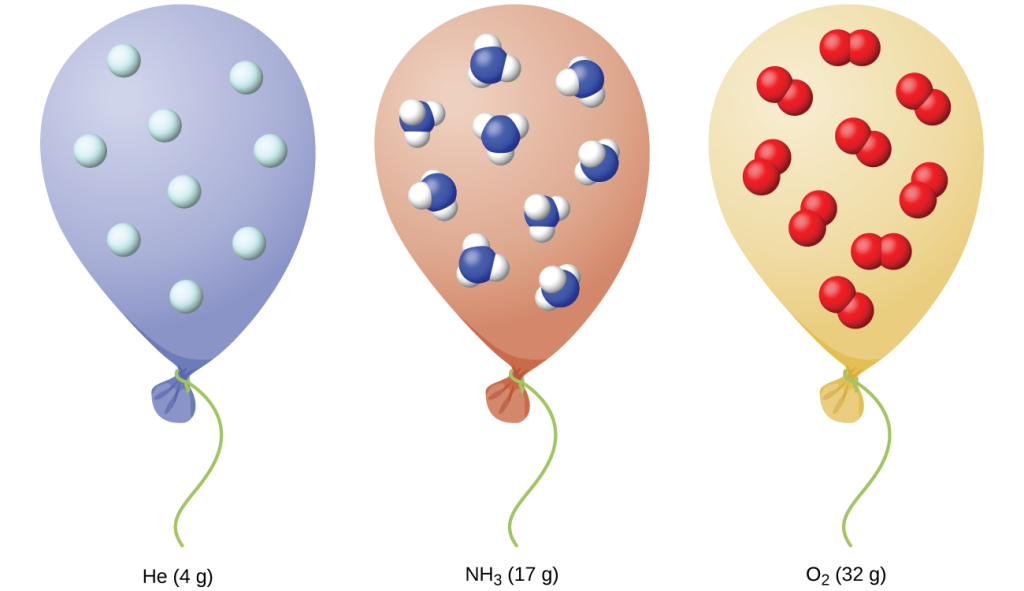
We have seen that the volume of a given quantity of gas and the number of molecules (moles) in a given volume of gas vary with changes in pressure and temperature. Chemists sometimes make comparisons against a standard temperature and pressure (STP) for reporting properties of gases: 273.15 K and 1 atm (101.325 kPa).1 At STP, one mole of an ideal gas has a volume of about 22.4 L—this is referred to as the standard molar volume (Figure 16).
Footnotes
- The IUPAC definition of standard pressure was changed from 1 atm to 1 bar (100 kPa) in 1982, but the prior definition remains in use by many literature resources and will be used in this text.
Key Concepts
- A relationship where one quantity is a constant multiplied by another quantity is called direct variation.
- Direct Variation : \( y = k x^n \) , \( k \) is a non zero constant
- Two variables that are directly proportional to one another will have a constant ratio.
- A relationship where one quantity is a constant divided by another quantity is called inverse variation.
- Inverse Variation : \( y = \frac{k}{ x^n} \) , \( k \) is a non zero constant
- Two variables that are inversely proportional to one another will have a constant multiple.
- In many problems, a variable varies directly or inversely with multiple variables. We call this type of relationship joint variation.
Section Exercises
Verbal
1. What is true of the appearance of graphs that reflect a direct variation between two variables?
Show Solution
The graph will have the appearance of a power function.
2. If two variables vary inversely, what will an equation representing their relationship look like?
3. Is there a limit to the number of variables that can vary jointly? Explain.
Show Solution
No. Multiple variables may jointly vary.
Algebraic
For the following exercises, write an equation describing the relationship of the given variables.
4. \( y \) varies directly as \( x \) and when \( x = 6 \), \( y =12\).
5. \( y \) varies directly as the square of \( x \) and when \( x = 4 \), \( y =80\).
Show Solution
\( y = 5 x^2 \)
6. \( y \) varies directly as the square root of \( x \) and when \( x = 36 \), \( y =24\).
7. \( y \) varies directly as the cube of \( x \) and when \( x = 36 \), \( y =24\).
Show Solution
\( y = \frac{1}{1944} x^3 \)
8. \( y \) varies directly as the cube root of \( x \) and when \( x = 27 \), \( y =15\).
9. \( y \) varies directly as the fourth power of \( x \) and when \( x = 1 \), \( y = 6\).
Show Solution
\( y = 6 x^4 \)
10. \( y \) varies inversely as \( x \) and when \( x = 4 \), \( y = 2 \).
11. \( y \) varies inversely as the square of \( x \) and when \( x = 3 \), \( y = 2 \).
Show Solution
\( y = \frac{18} {x^2 } \)
12. \( y \) varies inversely as the cube of \( x \) and when \( x = 2 \), \( y = 5 \).
13. \( y \) varies inversely as the fourth power of \( x \) and when \( x = 3 \), \( y = 1 \).
Show Solution
\( y = \frac{81} {x^4 } \)
14. \( y \) varies inversely as the square root of \( x \) and when \( x = 25 \), \( y = 3 \).
15. \( y \) varies inversely as the cube root of \( x \) and when \( x = 64 \), \( y = 5 \).
Show Solution
\( y = \frac{20} { \sqrt [3] {x}}\)
16. \( y \) varies jointly with \( x \) and \( z \) and when \( x = 2 \) and \( z = 3 \), \( y = 36 \).
17. \( y \) varies jointly with \( x \), \( z \) and \( w \) and when \( x = 1 \), \( z = 2 \), \( w = 5 \) then \( y = 100 \).
Show Solution
\( y = 1000 x w z\)
18. \( y \) varies jointly as the square of \( x \) and the square of \( z \) and when \( x = 3 \) and \( z = 4 \) then \( y = 72 \).
19. \( y \) varies jointly as \( x \) and the square root of \( z \) and when \( x = 2 \) and \( z = 25 \) then \( y = 100 \).
Show Solution
\( y = 10 x \sqrt{ z} \)
20. \( y \) varies jointly as the square of \( x \) and the cube of \( z \) and the square root of \( w \). When \( x = 1 \), \( z = 2 \), and \( w = 36 \), then \( y = 48 \).
21. \( y \) varies jointly as \( x \) and \( z \) and inversely as \( w \). When \( x = 3 \), \( z = 5 \), and \( w = 6 \), then \( y = 10\).
Show Solution
\( y = 4 \frac{xz}{w} \)
22. \( y \) varies jointly as the square of \( x \) and the square root of \( z \) and inversely as the cube of \( w \). When \( x = 3 \), \( z = 4 \), and \( w = 3 \), then \( y = 6\).
23. \( y \) varies jointly as \( x \) and \( z \) and inversely as the square root of \( w \) and the square of \( t \). When \( x = 3 \), \( z = 1 \), \( w = 25 \) and \( t = 2 \), , then \( y = 6\).
Show Solution
\( y = 40 \frac{xz}{\sqrt{w} t^2} \)
Numeric
For the following exercises, use the given information to find the unknown value.
24. \( y \) varies directly as \( x \). When \( x = 3 \), then \( y = 12 \). Find \( y \) when \( x = 20 \).
25. \( y \) varies directly as the square of \( x \). When \( x = 2 \), then \( y = 16 \). Find \( y \) when \( x = 8 \).
Show Solution
\( y = 256 \)
26. \( y \) varies directly as the cube of \( x \). When \( x = 3 \), then \( y = 5\). Find \( y \) when \( x = 4 \).
27. \( y \) varies directly as the square root of \( x \). When \( x = 16 \), then \( y = 4\). Find \( y \) when \( x = 36 \).
Show Solution
\( y = 6 \)
28. \( y \) varies directly as the cube root of \( x \). When \( x = 125 \), then \( y = 15\). Find \( y \) when \( x = 1,000 \).
29. \( y \) varies inversely with \( x \). When \( x = 3 \), then \( y = 2\). Find \( y \) when \( x = 1 \).
Show Solution
\( y = 6 \)
30. \( y \) varies inversely with the square of \( x \). When \( x = 4 \), then \( y = 3 \). Find \( y \) when \( x = 2 \).
31. \( y \) varies inversely with the cube of \( x \). When \( x = 3 \), then \( y = 1 \). Find \( y \) when \( x = 1 \).
Show Solution
\( y = 27 \)
32. \( y \) varies inversely with the square root of \( x \). When \( x = 64 \), then \( y = 12 \). Find \( y \) when \( x = 36 \).
33. \( y \) varies inversely with the cube root of \( x \). When \( x = 27 \), then \( y = 5 \). Find \( y \) when \( x = 125 \).
Show Solution
\( y = 3 \)
34. \( y \) varies jointly as \( x \) and \( z \). When \( x = 4 \) and \( z = 2 \), then \( y = 16 \). Find \( y \) when \( x = 3 \) and \( z = 3 \).
35. \( y \) varies jointly as \( x \), \( z \), and \( w \). When \( x = 2 \), \( z = 1\), and \( w = 2 \), then \( y = 72 \). Find \( y \) when \( x = 1 \), \( z = 2 \), and \( w = 3 \).
Show Solution
\( y = 18 \)
36. \( y \) varies jointly as \( x \) and the square root of \( z \). When \( x = 2 \) and \( z = 4\), then \( y = 144 \). Find \( y \) when \( x = 4 \) and \( z = 5 \).
37. \( y \) varies jointly as the square of \( x \) and the square root of \( z \). When \( x = 2 \) and \( z = 9\), then \( y = 24 \). Find \( y \) when \( x = 3 \) and \( z =2 5 \).
Show Solution
\( y = 90 \)
38. \( y \) varies jointly as \( x \) and \( z \) and inversely as \( w \). When \( x = 5 \), \( z = 2\), and \( w = 20\), then \( y = 4 \). Find \( y \) when \( x = 3 \), \( z = 8 \), and \( w = 48 \).
39. \( y \) varies jointly as the square of \( x \) and the cube of \( z \) and inversely as the square root of \( w \). When \( x = 2 \), \( z = 2\), and \( w = 64\), then \( y = 12 \). Find \( y \) when \( x = 1 \), \( z = 3 \), and \( w = 4 \).
Show Solution
\( y = \frac{81}{2} \)
40. \( y \) varies jointly as the square of \( x \) and of \( z \) and inversely as the square root of \( w \) and of \( t \). When \( x = 2 \), \( z = 3\), \( w = 16\), and \( t = 3 \), then \( y = 1 \). Find \( y \) when \( x = 3 \), \( z = 2 \), \( w =36 \) and \( t= 3\).
Technology
For the following exercises, use a calculator to graph the equation implied by the given variation.
41. \( y \) varies directly with the square of \( x \) and when \( x =2 \), \( y = 3 \).
Show Solution
\( y = \frac{3}{4} x^2 \)

42. \( y \) varies directly with the cube of \( x \) and when \( x =2 \), \( y = 4 \).
43. \( y \) varies directly with the square root of \( x \) and when \( x =36 \), \( y = 2 \).
Show Solution
\( y = \frac{1}{3} \sqrt{x} \)

44. \( y \) varies inversely with \( x \) and when \( x =6 \), \( y = 2 \).
45. \( y \) varies inversely as the square of \( x \) and when \( x =1 \), \( y = 4 \).
Show Solution
\( y = \frac{4}{x^2} \)

Extensions
For the following exercises, use Kepler’s Law, which states that the square of the time, \( T \) required for a planet to orbit the Sun varies directly with the cube of the mean distance, \( a \) that the planet is from the Sun.
46. Using Earth’s time of 1 year and mean distance of 93 million miles, find the equation relating \( T \) and \( a \).
47. Use the result from the previous exercise to determine the time required for Mars to orbit the Sun if its mean distance is 142 million miles.
Show Solution
\( 1.89 \text{years} \)
48. Using Earth’s distance of 150 million kilometers, find the equation relating \( T \) and \( a \).
49. Use the result from the previous exercise to determine the time required for Venus to orbit the Sun if its mean distance is 108 million kilometers.
Show Solution
\( 0.61 \text{years} \)
50. Using Earth’s distance of 1 astronomical unit (A.U.), determine the time for Saturn to orbit the Sun if its mean distance is 9.54 A.U.
Real-World Applications
For the following exercises, use the given information to answer the questions.
51. The distance \( s \) that an object falls varies directly with the square of the time, \( t \), of the fall. If an object falls 16 feet in one second, how long for it to fall 144 feet?
Show Solution
\( 3 \text{ seconds} \)
52. The velocity \( v \) of a falling object varies directly to the time, \( t \), of the fall. If after 2 seconds, the velocity of the object is 64 feet per second, what is the velocity after 5 seconds?
53. The rate of vibration of a string under constant tension varies inversely with the length of the string. If a string is 24 inches long and vibrates 128 times per second, what is the length of a string that vibrates 64 times per second?
Show Solution
\( 48 \text{ inches} \)
54. The volume of a gas held at constant temperature varies indirectly as the pressure of the gas. If the volume of a gas is 1200 cubic centimeters when the pressure is 200 millimeters of mercury, what is the volume when the pressure is 300 millimeters of mercury?
55. The weight of an object above the surface of Earth varies inversely with the square of the distance from the center of Earth. If a body weighs 50 pounds when it is 3960 miles from Earth’s center, what would it weigh it were 3970 miles from Earth’s center?
Show Solution
\( 49.75 \text{ pounds} \)
56. The intensity of light measured in foot-candles varies inversely with the square of the distance from the light source. Suppose the intensity of a light bulb is 0.08 foot-candles at a distance of 3 meters. Find the intensity level at 8 meters.
57. The current in a circuit varies inversely with its resistance measured in ohms. When the current in a circuit is 40 amperes, the resistance is 10 ohms. Find the current if the resistance is 12 ohms.
Show Solution
\( 33.33 \text{amperes} \)
58. The force exerted by the wind on a plane surface varies jointly with the square of the velocity of the wind and with the area of the plane surface. If the area of the surface is 40 square feet surface and the wind velocity is 20 miles per hour, the resulting force is 15 pounds. Find the force on a surface of 65 square feet with a velocity of 30 miles per hour.
59. The horsepower (hp) that a shaft can safely transmit varies jointly with its speed (in revolutions per minute (rpm) and the cube of the diameter. If the shaft of a certain material 3 inches in diameter can transmit 45 hp at 100 rpm, what must the diameter be in order to transmit 60 hp at 150 rpm?
Show Solution
\( 2.88 \text{inches} \)
60. The kinetic energy \( K \) of a moving object varies jointly with its mass \( m \) and the square of its velocity \( v \). If an object weighing 40 kilograms with a velocity of 15 meters per second has a kinetic energy of 1000 joules, find the kinetic energy if the velocity is increased to 20 meters per second.
Glossary
Constant of Variation
the non-zero value \( k \) that helps define the relationship between variables in direct or inverse variation.
Direct Variation
- the relationship between two variables that are a constant multiple of each other; as one quantity increases, so does the other
Inverse Variation
- the relationship between two variables in which the product of the variables is a constant
Joint Variation
- a relationship where a variable varies directly or inversely with multiple variables
Media Attributions
- 5.7 Figure 1 © OpenStax College Algebra with Corequisite Support 2e is licensed under a CC BY (Attribution) license
- 5.7 Figure 2 © OpenStax College Algebra with Corequisite Support 2e is licensed under a CC BY (Attribution) license
- 5.7 Figure 3 © OpenStax College Algebra with Corequisite Support 2e is licensed under a CC BY (Attribution) license
- 5.7 Figure 4 © OpenStax College Algebra with Corequisite Support 2e is licensed under a CC BY (Attribution) license
- 5.7 Figure 5 © OpenStax College Algebra with Corequisite Support 2e is licensed under a CC BY (Attribution) license
- 5.7 Figure 6 © OpenStax College Algebra with Corequisite Support 2e is licensed under a CC BY (Attribution) license
- 5.7 Figure 7 © Chemistry: Atoms First 2e | OpenStax is licensed under a CC BY (Attribution) license
- 5.7 Figure 8 © Chemistry: Atoms First 2e | OpenStax is licensed under a CC BY (Attribution) license
- 5.7 Figure 8 © Chemistry: Atoms First 2e | OpenStax is licensed under a CC BY (Attribution) license
- 5.7 Figure 10 © Chemistry: Atoms First 2e | OpenStax is licensed under a CC BY (Attribution) license
- 5.7 Figure 11 © Chemistry: Atoms First 2e | OpenStax is licensed under a CC BY (Attribution) license
- 5.7 Figure 12 © Chemistry: Atoms First 2e | OpenStax is licensed under a CC BY (Attribution) license
- 5.7 Figure 13 © Chemistry: Atoms First 2e | OpenStax is licensed under a CC BY (Attribution) license
- 5.7 Figure 14 © Chemistry: Atoms First 2e | OpenStax is licensed under a CC BY (Attribution) license
- 5.7 Figure 15 © Chemistry: Atoms First 2e | OpenStax is licensed under a CC BY (Attribution) license
- 5.7 Figure 16 © Chemistry: Atoms First 2e | OpenStax is licensed under a CC BY (Attribution) license

