Dynamics and the Laws of Motion

Motion draws our attention. Motion itself can be beautiful, causing us to marvel at the forces needed to achieve spectacular motion, such as that of a dolphin jumping out of the water, or a pole vaulter, or the flight of a bird, or the orbit of a satellite. The study of motion is kinematics, but kinematics only describes the way objects move—their velocity and their acceleration. The study of dynamics considers the forces that affect the motion of moving objects and systems. Newton’s laws of motion are the foundation of dynamics. These laws provide an example of the breadth and simplicity of principles under which nature functions. They are also universal laws in that they apply to similar situations on Earth as well as in space.

Dynamics is the study of the forces that cause objects and systems to move. To understand this, we need a working definition of force. Our intuitive definition of force—that is, a push or a pull—is a good place to start. We know that a push or pull has both magnitude and direction (therefore, it is a vector quantity) and can vary considerably in each regard. For example, a cannon exerts a strong force on a cannonball that is launched into the air. In contrast, Earth exerts only a tiny downward pull on a flea. Our everyday experiences also give us a good idea of how multiple forces add together.

Experience suggests that an object at rest will remain at rest if left alone, and that an object in motion tends to slow down and stop unless some effort is made to keep it moving. What Newton’s first law of motion states, however, is the following:

Newton’s First Law of Motion

Newton's first law of motion states that a body at rest remains at rest or, if in motion, remains in motion at a constant velocity unless acted on by a net external force. This is also called the law of inertia.

Note the repeated use of the verb “remains.” We can think of this law as preserving the status quo of motion.

Rather than contradicting our experience, Newton’s first law of motion states that there must be a cause (which is a net external force) for there to be any change in velocity (either a change in magnitude or direction). We will define net external force in the next section. An object sliding across a table or floor slows down due to the net force of friction acting on the object. If friction disappeared, would the object still slow down?

The idea of cause and effect is crucial in accurately describing what happens in various situations. For example, consider what happens to an object sliding along a rough horizontal surface. The object quickly grinds to a halt. If we spray the surface with talcum powder to make the surface smoother, the object slides farther. If we make the surface even smoother by rubbing lubricating oil on it, the object slides even further. Extrapolating to a frictionless surface, we can imagine the object sliding in a straight line indefinitely. Friction is thus the cause of the slowing (consistent with Newton’s first law). The object would not slow down at all if friction were completely eliminated. Consider an air hockey table. When the air is turned off, the puck slides only a short distance before friction slows it to a stop. However, when the air is turned on, it creates a nearly frictionless surface, and the puck glides long distances without slowing down. Additionally, if we know enough about the friction, we can accurately predict how quickly the object will slow down. Friction is an external force.

Newton’s first law is completely general and can be applied to anything from an object sliding on a table to a satellite in orbit to blood pumped from the heart. Experiments have thoroughly verified that any change in velocity (speed or direction) must be caused by an external force. The idea of generally applicable or universal laws is important not only here—it is a basic feature of all laws of physics. Identifying these laws is like recognizing patterns in nature from which further patterns can be discovered. The genius of Galileo, who first developed the idea for the first law, and Newton, who clarified it, was to ask the fundamental question, “What is the cause?” Thinking in terms of cause and effect is a worldview fundamentally different from the typical ancient Greek approach, when questions such as “Why does a tiger have stripes?” would have been answered in Aristotelian fashion: “That is the nature of the beast.” True perhaps, but not a useful insight.

Newton’s second law of motion is closely related to Newton’s first law of motion. It mathematically states the cause and effect relationship between force and changes in motion. Newton’s second law of motion is more quantitative and is used extensively to calculate what happens in situations involving a force.

Newton’s Second Law of Motion

Before we can write down Newton’s second law as a simple equation giving the exact relationship of force, mass, and acceleration, we need to sharpen some ideas that have already been mentioned. First, what do we mean by a change in motion? The answer is that a change in motion is equivalent to a change in velocity. A change in velocity means, by definition, that there is an acceleration. Newton’s first law says that a net external force causes a change in motion; thus, we see that a net external force causes acceleration. Another question immediately arises. What do we mean by an external force? An intuitive notion of external is correct—an external force acts from outside the system (object or collection of objects) of interest.

For example, in Figure 3.2(a) the system of interest is the wagon plus the child in it. The two forces exerted by the other children are external forces. An internal force acts between elements of the system. Again looking at Figure 3.2(a), the force the child in the wagon exerts to hang onto the wagon is an internal force between elements of the system of interest. Only external forces affect the motion of a system, according to Newton’s first law. You must define the boundaries of the system before you can determine which forces are external.

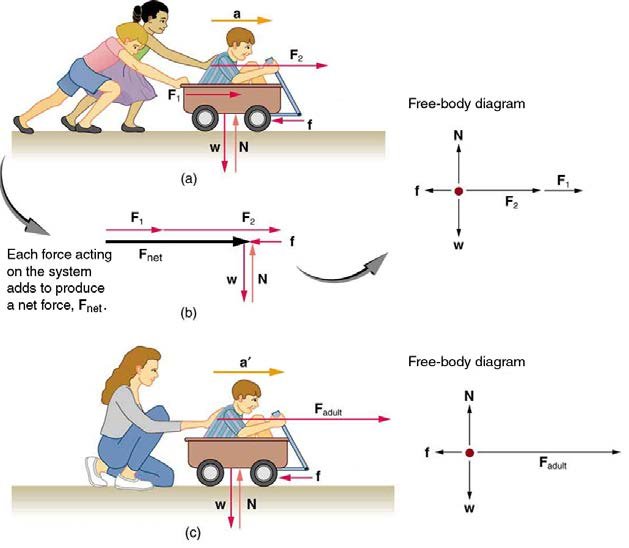
Now, it seems reasonable that acceleration should be directly proportional to and in the same direction as the net (total) external force acting on a system. This assumption has been verified experimentally and is illustrated in Figure 3.2. In part (a), a smaller force causes a smaller acceleration than the larger force illustrated in part (c). For completeness, the vertical forces are also shown; they are assumed to cancel since there is no acceleration in the vertical direction. The vertical forces are the weight w and the support of the ground N, and the horizontal force f represents the force of friction. These will be discussed in more detail in later sections. For now, we will define friction as a force that opposes the motion past each other of objects that are touching. Figure 3.2(b) shows how vectors representing the external forces add together to produce a net force, F_net or ∑F.

Newton's second law of motion is that the acceleration of a system is directly proportional to and in the same direction as the net external force acting on the system, and inversely proportional to its mass.

In equation form, Newton’s second law of motion is

a = ∑F/m

This is often written in the more familiar form

∑F = ma

Although these two equations are really the same, the first gives more insight into what Newton’s second law means. The law is a cause and effect relationship among three quantities that is not simply based on their definitions. The validity of the second law is completely based on experimental verification.

Units of Force

The equation, ∑F = ma, is used to define the units of force in terms of the three basic units for mass, length, and time. The SI unit of force is called the newton (abbreviated N) and is the force needed to accelerate a 1 kg system at the rate of 1 m/s². That is, since ∑F = ma,

1 N = 1 kg⋅m/s²

While almost the entire world uses the newton for the unit of force, in the United States, the most familiar unit of force is the pound (lb), where 1 N = 0.225 lb.

Net external force is the sum of all of the forces acting on an object. For example, if there is a force with a magnitude of 8 newtons in the positive direction and a force with a magnitude of 7 newtons in the negative direction on an object, the net external force would be 8 + (−7) = 1 newton. If the forces acting on an object are of equal magnitude in opposite directions, the net external force would be equal to 0.

Example 3.1

WHAT ACCELERATION CAN A PERSON PRODUCE WHEN PUSHING A LAWN MOWER?

Suppose that the net external force (push minus friction) exerted on a lawn mower is 51 N (about 11 lb) parallel to the ground. The mass of the mower is 24 kg. What is its acceleration?

 

Strategy

Since ∑F and m are given, the acceleration can be calculated directly from Newton’s second law as stated in ∑F = ma.

Solution

The magnitude of the acceleration a is a = ∑F/m. Entering known values gives

a = 51 N/24 kg

Substituting the units kg⋅m/s² for N yields

a = (51 kg⋅m/s²)/224 kg = 2.1 m/s²

Discussion

The direction of the acceleration is the same direction as that of the net force, which is parallel to the ground. There is no information given in this example about the individual external forces acting on the system, but we can say something about their relative magnitudes. For example, the force exerted by the person pushing the mower must be greater than the friction opposing the motion (since we know the mower moves forward), and the vertical forces must cancel if there is to be no acceleration in the vertical direction (the mower is moving only horizontally). The acceleration found is small enough to be reasonable for a person pushing a mower. Such an effort would not last too long because the person’s top speed would soon be reached.

There is a passage in the musical Man of la Mancha that relates to Newton’s third law of motion. Sancho, in describing a fight with his wife to Don Quixote, says, “Of course I hit her back, Your Grace, but she’s a lot harder than me and you know what they say, ‘Whether the stone hits the pitcher or the pitcher hits the stone, it’s going to be bad for the pitcher.’” This is exactly what happens whenever one body exerts a force on another—the first also experiences a force (equal in magnitude and opposite in direction). Numerous common experiences, such as stubbing a toe or throwing a ball, confirm this. It is precisely stated in Newton’s third law of motion.

Newton’s Third Law of Motion

Whenever one body exerts a force on a second body, the first body experiences a force that is equal in magnitude and opposite in direction to the force that it exerts. This is Newton's third law of motion.

This law represents a certain symmetry in nature: Forces always occur in pairs, and one body cannot exert a force on another without experiencing a force itself. We sometimes refer to this law loosely as “action-reaction,” where the force exerted is the action and the force experienced as a consequence is the reaction. Newton’s third law has practical uses in analyzing the origin of forces and understanding which forces are external to a system.

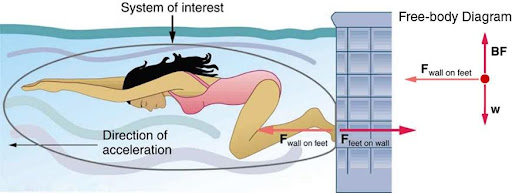
We can readily see Newton’s third law at work by taking a look at how people move about. Consider a swimmer pushing off from the side of a pool, as illustrated in Figure 3.4. She pushes against the pool wall with her feet and accelerates in the direction opposite to that of her push. The wall has exerted an equal and opposite force back on the swimmer. You might think that two equal and opposite forces would cancel, but they do not because they act on different systems. In this case, there are two systems that we could investigate: the swimmer or the wall. If we select the swimmer to be the system of interest, as in the figure, then F_{wall on feet} is an external force on this system and affects its motion. The swimmer moves in the direction of F_{wall on feet}. In contrast, the force F_{feet on wall} acts on the wall and not on our system of interest. Thus F_{feet on wall} does not directly affect the motion of the system and does not cancel F_{wall on feet}. Note that the swimmer pushes in the direction opposite to that in which she wishes to move. The reaction to her push is thus in the desired direction.

 

Link to Learning

Use this interactive simulation by PhET to see Newton’s Laws in action (opens in new window): Forces and Motion.

Other examples of Newton’s third law are easy to find. As a professor paces in front of a whiteboard, she exerts a force backward on the floor. The floor exerts a reaction force forward on the professor that causes her to accelerate forward. Similarly, a car accelerates because the ground pushes forward on the drive wheels in reaction to the drive wheels pushing backward on the ground. You can see evidence of the wheels pushing backward when tires spin on a gravel road and throw rocks backward. In another example, rockets move forward by expelling gas backward at high velocity. This means the rocket exerts a large backward force on the gas in the rocket combustion chamber, and the gas therefore exerts a large reaction force forward on the rocket. This reaction force is called thrust. It is a common misconception that rockets propel themselves by pushing on the ground or on the air behind them. They actually work better in a vacuum, where they can more readily expel the exhaust gases. Helicopters similarly create lift by pushing air down, thereby experiencing an upward reaction force. Birds and airplanes also fly by exerting force on air in a direction opposite to that of whatever force they need. For example, the wings of a bird force air downward and backward in order to get lift and move forward. An octopus propels itself in the water by ejecting water through a funnel from its body, similar to a jet ski. In a situation similar to Sancho’s, professional cage fighters experience reaction forces when they punch, sometimes breaking their hand by hitting an opponent’s body.

What It Means to Do Work

The scientific definition of work differs in some ways from its everyday meaning. Certain things we think of as hard work, such as writing an exam or carrying a heavy load on level ground, are not work as defined by a scientist. The scientific definition of work reveals its relationship to energy—whenever work is done, energy is transferred.

For work, in the scientific sense, to be done, a force must be exerted and there must be displacement in the direction of the force.

Link to Learning

Use this interactive simulation to view the relationships between distance, work, and force (opens in new window): PhET Balancing Act Simulation. Here, the only acceleration that is acted on these objects is their gravitational acceleration. Knowing that they all have the same acceleration, we can view the variation of mass across objects to be proportional to the force acted on those objects. Why does it make sense that when distance increases and work stays the same, the force decreases?  If the work does not change, the force must decrease when the distance increases in order to maintain a balanced equation.

What Is Work?

The work done on a system by a constant force is the product of the component of the force in the direction of motion times the distance through which the force acts. For one-way motion in one dimension, this is expressed in equation form as:

W = |F|(cosθ)|d|

where W is work,  d is the displacement, and θ is the angle between the force vector F and the displacement vector d. We can also write this as:

W = Fd cos θ

What Is Power?

Power—the word conjures up many images: a professional football player muscling aside his opponent, a dragster roaring away from the starting line, a volcano blowing its lava into the atmosphere, or a rocket blasting off, as in Figure 3.5.

Power is the rate at which work is done.

P = W/t

The SI unit for power is the watt (W), where 1 watt equals 1 joule/second (1 W = 1 J/s)

Because work is energy transfer, power is also the rate at which energy is expended. A 60-W light bulb, for example, expends 60 J of energy per second. Great power means a large amount of work or energy developed in a short time. For example, when a powerful car accelerates rapidly, it does a large amount of work and consumes a large amount of fuel in a short time.

These images of power have in common the rapid performance of work, consistent with the scientific definition of power (P) as the rate at which work is done.

 

Simple Machines

A simple machine is a mechanical device that allows you to do the same amount of work with reduced effort by increasing the distance traveled to decrease the force. The six basic simple machines are the wheel and axle, inclined plane (or ramp), pulley, lever, wedge, and screw.

Check Your Understanding

 

The content in this chapter  is adapted from multiple sources. The overall chapter structure is adapted from Exploring the Physical World and used under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The sections on dynamics, Newton’s laws of motion, work and power, and simple machines are adapted from College Physics 2e by OpenStax  and are used under a Creative Commons-Attribution 4.0 International License.  Other content and interactive activities are the original work of the authors of this text and are shared under a Creative Commons-Attribution 4.0 International License.