As we will see, their ambitions were even grander since they also argued that much of what was going on in philosophy at the time was literally meaningless.

We will consider three central projects taken on by the Positivists in developing their Empiricist view of scientific knowledge.

These are the demarcation problem, the problem of distinguishing science from non-science, developing a view about what a scientific theory is, and giving an account of scientific explanation. The Positivists utilize the resources of symbolic logic in each of these projects.

The Demarcation Problem

Among the main tasks the Positivists set for themselves was that of distinguishing legitimate science from other rather suspect fields and methods of human inquiry. Specifically, they wanted to distinguish science from religion, metaphysics, and pseudo-science like astrology.

19th century German metaphysics involved attempts to reason about such obscure notions as “the absolute,” or the nature of “the nothing.” Such metaphysics needed to be distinguished from genuine science. We had also seen appeal to obscure empirically suspicious entities and forces in Aristotelian science such as the “vital force” to explain life, or the “dormative virtue” a mysterious power of substances like opium to cause sleep. Such mysterious forces needed to be eliminated from genuine scientific discourse.

While metaphysics and talk of obscure forces in science were to be distinguished from genuine science, the Positivists needed to preserve a role for unobservable theoretical entities like atoms and electrons. The rejection of metaphysics and obscure forces must not undermine the legitimate role for theoretical entities.

The Positivists employed Empiricism in their proposed solution to the demarcation problem. Empiricism, as we know, is just the view that our sense experience is the ultimate source of justification for all of our factual knowledge of the world. The Positivists extend Empiricism to cover not just the justification of knowledge, but the meaningfulness of language as well. That is, they take the source of all meaning to ultimately be our sense experience. Only meaningful statements can be true or false. So, only statements whose meaning can ultimately be given in observational terms can be true or false. Theoretical terms like “atom” refer to things we can’t directly observe. But talk about such theoretical entities could be made empirically respectable by means of observational tests for when theoretical terms are being appropriately applied. Electrical charge, for instance, is not itself observable. But we can define theoretical terms in terms of observational tests for determining whether the term applies. So we might say that a thing is in a state of electrical charge if it registers voltage when electrodes are attached and hooked up to a voltage meter. Similarly, though you don’t directly observe the state of charge of a battery, you can easily carry out a test in observational terms by putting the battery in a flashlight and seeing if it lights up.

This doctrine about meaning was called the Verificationist Theory of Meaning (VTM). The Verificationist Theory of Meaning has it that a sentence counts as meaningful only if we can specify the observable conditions under which it would count as true or false.

This view can then be used to distinguish empirically respectable language from nonsense. Legitimate scientific discourse must count as meaningful on the Verifiability Theory of Meaning. So we have a view on which science is distinguished as meaningful while pseudo-science, religion, poetry etc. are, strictly speaking, meaningless. Likewise, most of philosophy turns out to be meaningless as well. Not only will obscure 19th-century German metaphysics turn out to be meaningless, but talk of free will, immaterial substances, and all of ethics will likewise turn out to be meaningless. The only legitimate role left for philosophers, according to the Logical Positivists, will be the logical analysis of scientific discourse. Being meaningless, religion, pseudo-science, most of philosophy, literature, etc. is neither true nor false. While these things cannot be true or false, according to Positivists’ criteria for meaningfulness, they may provide helpful expressions of human emotions, attitudes towards life, etc. That is, poetry, literature, religion, and most philosophy will be merely so much comforting or disturbing babble, mere coos, squeals, or screams.

Significant progress is made by paying close attention to the meaningfulness of scientific discourse. But the Verificationist Theory of Meaning eventually falls apart for a number of reasons including that it turns out not to be meaningful according to its own criteria. Amusingly, we can’t provide an empirical test of truth or falsity for the claim that a claim is meaningful only if we can provide an empirical test for its truth or falsity. That is, according to the Verificationist Theory of Meaning, the term “meaning” turns out to be meaningless. Logical Positivism remained a powerful influence in philosophy through much of the 20th century and it did serve to weed out some pretty incomprehensible metaphysics. But I can now happily report that other important areas of philosophy, notably ethics and metaphysics, have recovered from the Positivists’ assault on philosophy from within.

Theories

Understanding the Logical Positivist view of theories requires that we say a few things about formal languages. The symbolic logic developed in Russell and Whitehead’s Principia Mathematica is a formal language. Computer languages are also formal languages.

A formal language is a precisely specified artificial language. A formal language is specified by doing three things:

1. identify the language’s vocabulary.
2. identify what counts as a well formed expression of that language.
3. give axioms or rules of inference that allow you to transform certain kinds of well formed expressions into other kinds of well formed expressions.

Scientific theories are formal languages according to the Positivists. We can understand what this means by considering the component parts of a scientific theory and how these map on to the elements of formal languages just given. A theory consists of the formal language of first order predicate logic with quantifiers (the logic developed first by Frege and then in greater detail by Russell and Whitehead) supplemented with observational vocabulary, correspondence rules that define theoretical terms in terms of observational vocabulary, and statements of laws like Galileo’s laws of motion, Newton’s law of universal gravitation, etc. All of the non-logical vocabulary of a scientific theory is definable in observational terms. Well formed expressions in scientific discourse will be only those expressible in terms of formal logic plus the vocabulary of science. The rules of inference in scientific discourse consist only of the rules of inference of logic and math plus scientific laws.

The Logical Positivist’s view of what a theory is has since been deemed overly formalized. There are numerous legitimate theories in science that can’t be rendered in a formal system. Consider theories in anthropology or geology for instance. Nevertheless, the idea of a theory as a formal system is a powerful one and it remains the gold standard in many sciences. Linguistics has “gone computational” in recent years, for instance. The most ambitious scientific undertaking in all of human history, the science of climate change, also aims to render theory and explanation in formal systems through massive and intricately detailed computer models of climate change. In fact, roughly speaking, we can consider a theory formalizable when it can be comprehensively modeled on a computer. Computer programs are paradigm examples of formal systems.

A further more general lesson we might take from the Positivist’s view of theories addresses a very commonplace misunderstanding of what a theory is. People commonly think of theories as just claims that lie on a scale of certainty being somewhat more certain than guesses or hypotheses, but rather less certain than established matters of fact. This is really a terrible misunderstanding of what a theory is. It is commonly invoked in fallacious attempts to discredit science, as when people dismiss evolution or climate change science as “just a theory.” Such comments reveal a basic misunderstanding of what theory is. For something to count as a theory has nothing to do with our level of certainty in its truth. Many scientific theories are among the best established scientific knowledge we have. A few years ago, for instance, some scientist claimed to have observed a particle in a particle accelerator travelling faster than the speed of light. It made the news and caused a bit of excitement. But those in the know, those who understand Einstein’s special relativity and the full weight of the evidence in support of it patiently waited for the inevitable revelation that some clocks had been miscalibrated. Einstein’s special relativity is right and we know this with about as much certainty as we can know anything. In the other direction, there are lots of genuine theories that we know full well to be false.

Aristotle’s physics would be one example. Having very much or very little confidence in something has nothing to do with whether it is properly called a theory.

So if it’s not about our degree of confidence, what does make something a theory? What makes something a theory is that it provides a general framework for explaining things. The Positivists didn’t discover this, but their idea of a theory as a formal system illustrates the idea nicely. Theories generally consist of a number of logically interconnected principles that can be mutually employed to explain and predict a range of observable phenomena. Bear this in mind as we consider the Positivist’s view of scientific explanation.

Explanation

According to the Deductive Nomological model of explanation developed by the Logical Positivist, Carl Hempel, a scientific explanation has the form of a deductively valid argument. The difference between an argument and an explanation is just their respective purposes. Formally, arguments and explanations look alike. But the purpose of an explanation is to shed light on something we accept as true, while the purpose of an argument is to give us a reason for thinking something is true. Given this difference in purpose, we call the claim that occupies the place of the conclusion the explanandum (it’s the fact to be explained), and the claims that occupy the place of the premises the explanans (these are the claims that, taken together, provide the explanation). In a scientific explanation, the explanans will consist of laws and factual claims. The factual claims in conjunction with the laws will deductively entail the explanandum.

For example, consider this explanation for why a rock falls to the earth:

1. F = GM1M2/r2, Newton’s law of universal gravitation which tells us that massive bodies experience a force of mutual attraction that is proportionate to their mass and inversely proportionate to the distance between them.
2. F = MA. This is the force law, which tells us that force equals mass times acceleration.
3. The rock has mass of 1 Kg.
4. The earth has a mass of 5.97219 × 1024 kilograms.
5. The rock was released within the gravitational field of the earth.
6. No forces prevented the rock from falling to the earth.
7. The rock fell to the earth.

Recall that deductive logic is part of every theory, every explanatory framework. The first two claims in this explanation are statements of law from Newtonian physics. The remaining four are statements of fact. Taken together, these six claims deductively entail the explanandum, that the rock fell to the earth. This should illustrate how theories function as explanatory frameworks.

One very useful thing Hempel’s account of explanation does is alert us to the argument-like structure of developed explanations.

The basic idea here is that a complete explanation should include all of the facts involved in making the fact to be explained true.

These will include both particular facts relevant to the specific fact we want explained and general principles (scientific laws in the case of scientific explanations) that belong to a broader framework for explanation. A fully developed explanation reveals a logical relationship between the fact we want to explain, other relevant facts and connecting principles like laws of nature.

Hempel’s account of explanation faced a number of problems that have helped to refine our understanding of scientific explanation.

We won’t address them here except to mention one because it’s amusing. Consider this explanation:

1. Men who take birth control pills do not get pregnant.
2. Bruce is a man and he takes birth control pills.
3. Bruce is not pregnant.

This seems to meet all of the positivist’s criteria for being an explanation. But aside from being silly, it’s at least not a very good explanation for why Bruce is not pregnant. Problem cases like this suggest that purely formal accounts of explanation like Hempel’s will fall short in sorting which facts are relevant in an explanation.

There is also a more general lesson I’d like you to take from the positivist’s account of explanation. For your entire career as a student you’ve been asked to explain things, but odds are nobody has ever really explained what it means to explain something.

Personally, I don’t think I had ever given a thought to what an explanation was until I encountered the Deductive Nomological account in a Philosophy of Science class. But now you’ve been introduced to a model of explanation. You may not find it fully applicable to every academic situation you encounter. But if you try to make use of it by thinking of explanations as having a developed argument-like structure, you might find grades in many of your classes improving significantly.

We mentioned at the outset that Logical Positivism was very much influenced by Hume’s Empiricism. You will recall that Hume argued for some surprising skeptical results. The Logical Positivists adopted one of two strategies for dealing with this. On some issues it was argued that Hume’s skeptical conclusions were acceptable, while on others Hume’s skepticism was regarded as a problem yet to be solved. As an example of the first strategy, Bertrand Russell, though not a Logical Positivist himself, wrote an influential paper in which he argued that science can proceed as usual without any reference to the notion of causation. Skepticism about necessary causal connections was deemed not to be problematic. Skepticism about induction was more difficult to accept. So the early 20th century saw a variety of sometimes colorful but generally unsuccessful attempts to resolve the problem of induction.

And this brings us to Karl Popper.

6.1: Karl Popper

6.2: Thomas Kuhn

6.3: Review and Discussion Questions

This page titled 6: Philosophy of Science is shared under a CC BY-NC 4.0 license and was authored, remixed, and/or curated by Russ W. Payne via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.

6.1.1 https://human.libretexts.org/@go/page/17596

6.1: Karl Popper

Karl Popper was a philosopher in Vienna during the reign of Logical Positivism, but he was not himself a Positivist. Popper is best known for his contributions to the problem of induction and the demarcation problem. In both cases his views were critical of the Logical Positivists.

Conjecture and Refutation

As you will recall, Hume argues that inductive arguments fail to provide rational support for their conclusions. His reason for taking induction to be irrational is that every inductive argument assumes that unobserved events will follow the pattern of observed events and this assumption cannot be supported either deductively or inductively. No purely deductive support can be given for this principle of induction because it is not a mere truth of logic. And any inductive argument offered in support of the inductive principle that unobserved cases will be like observed cases will be circular because it will also employ the very principle of induction it tries to support as a premise.

Popper accepted Hume’s conclusion that inductive inference is not rationally justifiable. He takes the problem of induction to have no adequate solution. But he rejects the further conclusion that science therefore yields no knowledge of the nature of the world.

With Hume, Popper holds that no number of cases offered as confirmation of a scientific hypothesis yields knowledge of the truth of that hypothesis. But just one observation that disagrees with a hypothesis can refute that hypothesis. So while empirical inquiry cannot provide knowledge of the truth of hypotheses through induction, it can provide knowledge of the falsity of hypotheses through deduction.

In place of induction, Popper offers the method of conjecture and refutation. Scientific hypotheses are offered as bold conjectures (guesses) about the nature of the world. In testing these conjectures through empirical experiment, we cannot give positive inductive reasons for thinking that they are true. But we can give reasons for thinking they are false. To see how this works, let’s look at the pattern of reasoning employed in testing a scientific hypothesis using induction on the one hand, and Popper’s deductive method of conjecture and refutation on the other. First, in designing an experiment, we determine what we should expect to observe if the hypothesis is true. Using induction, if our observation agrees with our expectation, we take the hypothesis to be inductively confirmed. The pattern of reasoning looks like this:

1. If H, then O
2. O
3. Therefore, H

This pattern of reasoning is not deductively valid (generate a counterexample to see for yourself), and as an inductive argument it faces the problem of induction. So this pattern of reasoning fails to provide us with rational grounds for accepting H as true. But suppose that when we carry out our experiment, we observe “not O.” In this case our pattern of reasoning looks like this:

1. If H, then O
2. not O
3. Therefore, not H

This pattern of reasoning is deductively valid. To see this try to suppose that the premises are true and the conclusion is false. If the conclusion were false, then “H” would be true. And, given this and the truth of the first premise, “O” would follow. But “O” contradicts “not O,” which is asserted by the second premise. So it is not possible for the premises to be true and the conclusion false. In other words, the pattern of reasoning here is deductively valid.

The latter is the pattern of reasoning used in the method of conjecture and refutation. It is a deductively valid pattern that makes no use of inductive confirmation. It should now be clear how Popper’s method of conjecture and refutation works and how empirical inquiry making use of this method can provide us with knowledge of the world (or rather, how the world isn’t) while avoiding the problem of induction.

According to Popper, there is no rational methodology or logic for evaluating how scientists come up with hypotheses. They are just conjectures and no amount of evidence is capable of inductively confirming hypotheses in the sense of giving us positive reason for thinking our hypotheses are true. Evidence in agreement with a hypothesis never provides it with inductive confirmation.

If all the evidence is in agreement with a hypothesis, we can say that it is “corroborated.” To say that a hypothesis is corroborated is just to say that it has survived our best attempts at refutation. But contrary evidence can decisively refute hypotheses.

6.1.2 https://human.libretexts.org/@go/page/17596

Demarcation through Falsifiability

The demarcation problem is the problem of distinguishing science from other things, from poetry to religion to obscure metaphysics. Popper offers an alternative to the Positivist’s verificationist theory of meaning in addressing this problem. The Positivist’s solution to the demarcation problem had the downside of denying that we can assert as true that it is wrong to torture innocent babies just for fun. Popper’s view of the matter avoids this unsavory consequence.

Popper’s method of conjecture and refutation suggests his criterion for distinguishing science from non-science. For it to be possible to refute a hypothesis requires that there be possible observations that would give us grounds for rejecting the hypothesis.

We can only scientifically investigate hypotheses that take observational risks, those that are exposed to the possibility of being shown false through observation. That is, we can take a hypothesis to be scientific if and only if it is falsifiable. For a hypothesis to be falsifiable we must be able to specify possible observational conditions that would be grounds for rejecting the hypothesis as false. But this does not mean that it will be proven false or that it can be shown to be false (either of these confusions would lead to the absurd view that a claim is only scientific if it is false). Let’s look at some examples to make this clear.

Consider the hypothesis that all crows are black. We can specify observable conditions under which we would count this as false.

Namely, seeing a white crow, or a green one. Being able to specify the observational conditions under which we would reject this hypothesis doesn’t mean that it is false. Suppose the hypothesis is true. It is still a claim that takes risks in the face of observation because we know that some possible observations would refute it. So the hypothesis that all crows are black is falsifiable.

Now consider claims made by astrology. These are typically formulated in such a vague way that any eventuality could be interpreted as affirming the astrologer’s predictions. If there are no possible observations that could refute astrology, then it is not scientific. Some astrologers might make specific and concrete predictions. These might get to claim that they are being scientific on Popper’s view, but to the degree that astrologers do take risks of being refuted by observation, they have been refuted too often.

Political ideologies often fail to pass the falsifiability test. Popper was especially critical of Marxism, which was very popular with the Viennese intellectuals he knew in his youth. Marxists seemed to have an explanation for everything. The inevitability of Marxist revolution was illustrated by its rising popularity in much of Europe. But if Americans, for instance, were not rebelling against their capitalist oppressors, it was only because they had yet to see how alienating capitalism is. The conditions for revolution just weren’t yet ripe. But they will be, says the confident Marxist. Popper’s key insight was that a theory that can explain everything that might happen doesn’t really explain anything. It is empty.

Today, Popper might make the same criticism of very different political ideologies. If free markets don’t fix every problem, the libertarian can always complain that this is only because they have not been allowed to function freely enough. If government doesn’t fix every problem, the big government liberal can always complain that big government hasn’t been empowered enough (when we get around to political philosophy we will find reason to doubt that there are very many liberals that really fit this stereotype). Extreme views are only made plausible to their fans by elaborate schemes of excuses for why they don’t work out as well as they should. Popper would say that in politics as in science, we need to try things where we can honestly examine the consequences and hold ourselves accountable when they don’t go well by trying something else.

Auxiliary Hypotheses

Here we will describe an objection to Popper’s method of conjecture and refutation that will set the stage for introducing the views of Thomas Kuhn. According to Popper, we make progress in science by refuting false conjectures. We never have inductive grounds for holding that proposed scientific hypotheses and explanations are true, but we can narrow in on the truth by eliminating the falsehoods. Our hypotheses lead us to expect certain observations. If we do not observe what we expect to observe, then we have non-inductive grounds for rejecting our hypothesis. Again, the pattern of reasoning followed in eliminating false hypotheses through scientific inquiry looks like this:

1. If H, then O
2. Not O
3. Therefore, not H

This is the deductively valid pattern of reasoning known as modus tollens. However, we rarely get to test hypotheses in isolation.

Typically, our expectation of a given observation is based on the hypothesis we are interested in testing in conjunction with any number of background assumptions. These background assumptions are the auxiliary hypotheses. If we take into account the auxiliary hypotheses, the pattern of reasoning used in Popper’s method of conjecture and refutation looks like this:

6.1.3 https://human.libretexts.org/@go/page/17596

1. If H and AH, then O
2. Not O
3. Therefore, not H

But this argument pattern is not valid. The observation (not O) might indicate the falsity of one of the auxiliary hypotheses (AH) rather than the falsity of (H), the hypothesis we set out to test. What this tells us is that the implications of other than expected observations are always ambiguous. When our observations don’t accord with our expectations, it tells us that at least one of the assumptions or hypotheses that lead us to expect a given observation is false. It may be the hypothesis we set out to test, or it may be one of our auxiliary hypotheses. But unexpected observations don’t tell us which is false.

Here’s a nice example of auxiliary hypotheses at work in everyday reasoning. Our hypothesis is that Hare is faster than Tortoise.

This hypothesis leads us to expect that Hare will win a race against Tortoise. But suppose that, contrary to our expectation, we observe Tortoise winning the race. The hypothesis that Hare is faster than Tortoise is not thereby falsified because of the presence of a number of auxiliary hypotheses. Among these auxiliary hypotheses are the following: (i) Hare did not stop in the middle of the race for a snack, (ii) Hare did not get run over while crossing the road, (iii) Hare did not get eaten by Coyote during the race, (iv) Hare did not get entangled in a philosophical discussion about the rationality of scientific methods with his friend Gopher before crossing the finish line. When Tortoise crosses the finish line first, that tells us that either Tortoise is faster than Hare or one of these or many other auxiliary hypotheses is false. But Tortoise winning doesn’t tell us which. The unexpected observation thus fails to cleanly refute our hypothesis.

This page titled 6.1: Karl Popper is shared under a CC BY-NC 4.0 license and was authored, remixed, and/or curated by Russ W. Payne via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.

6.2.1 https://human.libretexts.org/@go/page/17597

6.2: Thomas Kuhn

The Positivists and Karl Popper offer attempts to describe and develop rational methods for scientific inquiry. In so doing, they offer normative theories of scientific practice. That is, they offer views about how scientific inquiry should proceed and what counts as good scientific practice. Kuhn’s philosophy of science is inspired by the history of science and seeks to describe how science actually develops. Kuhn’s undertaking is not aimed at revealing universal norms of rational scientific practice. But his views have been taken by some to imply that the development of science is not guided by general norms of rationality, at least at crucial revolutionary periods of theory change.

Kuhn describes three stages in the development of a science. The first stage is called “pre-paradigm science.” In pre-paradigm science, people seeking to understand an observed phenomenon share no common stock of background theory. Each inquirer essentially starts from scratch. Under these circumstances, very little progress is made. We have nothing resembling a tradition that can be passed from one person on to her students for further development and investigation. The various theories of the nature of the world proposed by pre-Socratic philosophers might be considered an example of pre-paradigm physics.

At some point, someone develops an account of the observed phenomenon that has enough substance and explanatory power to attract the attention of a community of individuals who will then carry on inquiry along the proposed lines. This marks the beginnings of normal science. Kuhn calls the sort of account of the observed phenomenon that is required for this to happen a paradigm.

A paradigm consists of the following four things:

1. A body of theory including laws: For instance, the basic laws of motion.
2. Background metaphysical assumptions: For instance, that there is an external world and that our senses provide a reasonably reliable guide to its nature, that we share common objects of perception, etc.
3. Values: Here we have in mind primarily epistemological values including norms of rationality. The idea here is that a paradigm tells you what counts as a phenomenon that requires explanation and provides a standard for what counts as an adequate explanation of that phenomenon.
4. Exemplars: These are textbook applications of the theory to the phenomenon it is intended to explain. Classical physics is taught through exemplars that include applying Newton’s laws to swinging pendulums and forces exerted on springs.

Normal science, the second of Kuhn’s three stages, is carried out within a paradigm. Working within a paradigm, the scientist normally accepts the core elements of the paradigm as dogma. The scientist’s job in the stage of normal science is to work out the details of the paradigm without calling into question the central laws of the paradigm, or the epistemic standards it presupposes. In the normal stage, we can think of science as puzzle solving. Investigators are not advancing bold new theories, but applying the accepted theoretical framework in new and novel sorts of cases. During normal science, a paradigm gets worked out in detail.

In the course of normal science, problems that resist resolution with the paradigm often arise. If these “recalcitrant” problems remain long enough, they become what Kuhn calls anomalies. As the details of a paradigm get worked out, the anomalies become harder and harder to ignore. Researchers in need of projects may focus more and more scrutiny on the remaining anomalies.

Continued and intensified but unsuccessful attempts to resolve anomalies can give rise to a crisis in normal science. Such a crisis makes it possible to call into question core elements of the paradigm that had been previously held dogmatically.

Persistent anomalies in a science can provoke a crisis in which the paradigm itself is called into question. In this atmosphere, it is possible for scientists to propose and win wide acceptance for significant changes in the theoretical framework. Until persistent anomalies provide a crisis, however, the social conditions aren’t ripe for revolution. Even if someone had great revolutionary ideas, they simply won’t get a hearing with the community since it is committed to working out the details of the standing paradigm.

Revolutions in thinking can’t happen until the community is convinced that the old paradigm is irrevocably broken. When this does happen and an appropriate alternative to the old paradigm is developed and proposed, then and only then can what Kuhn calls a scientific revolution happen. In a scientific revolution, the scientific community abandons one paradigm in favor of another.

Once a new paradigm takes hold in the scientific community, normal science is resumed, the details of the new paradigm begin to get worked out and normal science continues until a new batch of anomalies emerges and provokes the next crisis.

A key insight of Kuhn’s is that science is a community effort. We often hold a “great genius” vision of the history of science where the fabulous insights of very special individuals are what drive science forward. Kuhn would say this is a distorted picture. The great geniuses like Newton or Einstein can only launch a revolution in scientific thinking when a broader community of inquirers have prepared the field and created the conditions for the germination of the seeds of a revolution in thinking. The history of science needs to be understood in terms of how these broader communities progress to the point where revolutionary thinking is called for and can be fruitful. The great insights and discoveries never happen in a social vacuum.

Kuhn thinks that the paradigm shift that occurs in the course of a scientific revolution is comparable to a gestalt switch as in the duck/rabbit image below.

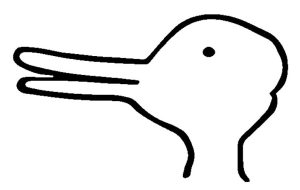
Seeing this image as a duck blocks out seeing it as a rabbit. Something similar happens in the case of a paradigm shift. In a paradigm shift one drops one conceptual framework in favor of another. When we grasp and evaluate the claims made in normal science, we do so in the context of acceptance of a paradigm. Kuhn suggests that the very meaning of the claims made in paradigm-based normal science can only be comprehended relative to the conceptual framework of that paradigm. A result of this is that from the perspective on one paradigm, we are never really in a position to evaluate the claims of normal science under a different paradigm. In this sense, paradigms are said to be incommensurable (lacking any common measure or independent standard of comparison).

It is tempting to see the cycle of normal science and revolutionary science as a Popper-style process of conjecture and refutation at the level of paradigms. However, Kuhn maintains that paradigms are never exactly refuted by intractable anomalies. Rather, when the scientific community enters a period of crisis and an attractive alternative to the old paradigm emerges, the community gives up on the old paradigm and adopts the new one. Paradigms are not so much refuted as abandoned. This raises serious questions about whether paradigm shifts in scientific revolutions can be understood as rational processes. They would seem not to be if we think of human rational processes as in some way rule driven like logical rules of inference. But we might instead take Kuhn to be revealing a richer view of human rationality.

On Kuhn’s view, the methods and standards of science get articulated and refined through periods of normal science and are liable to undergo bigger shifts in periods of scientific revolution. What counts as good scientific inquiry and investigation cannot be specified independent of its history. We figure out what works as we encounter new challenges. The history of science reveals the practice of science to be dynamic and adaptive. Creativity and resourcefulness go into the hard-earned advances in our understanding of the world.

The broader moral of this story is that we should be highly suspicious of any attempt to boil the methods of science down to any specific series of steps. Rather, a good understanding of the many methods of science can only be had through a study of its history, its successes, and its failures. And even at this, our appreciation of the methods of science must remain open ended. The story of science is far from finished, and so our understanding of its methods is likewise incomplete.

This page titled 6.2: Thomas Kuhn is shared under a CC BY-NC 4.0 license and was authored, remixed, and/or curated by Russ W. Payne via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.

6.3.1 https://human.libretexts.org/@go/page/17598

6.3: Review and Discussion Questions

1. How does the development of more powerful symbolic systems of logic boost Empiricism at the beginning of the 20th century?
2. Explain how the Logical Positivists extend Empiricism to the theory of meaning.
3. How is the verificationist theory of meaning used to address the demarcation problem?
4. What is a theory according to the Positivists?
5. Explain what’s wrong with the view that theories are just very well supported hypotheses that are still not so certain.
6. What does it mean to regard a theory as an explanatory framework?
7. How do the Logical Positivists understand explanation?
8. How would Popper resolve (not solve) the problem of induction?
9. How does Popper address the demarcation problem?
10. Explain how auxiliary hypotheses challenge Popper’s method of conjecture and refutation.
11. Explain pre-paradigm science. Why is little lasting progress made at this stage of science?
12. What is a paradigm?
13. How does normal science under a paradigm proceed?
14. What is an anomaly?
15. What conditions are necessary for a scientific revolution?
16. What does it mean to speak of competing paradigms as incommensurable?
17. How are the methods of science sensitive to its history?

This page titled 6.3: Review and Discussion Questions is shared under a CC BY-NC 4.0 license and was authored, remixed, and/or curated by Russ W. Payne via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.