Chapter 4 Linear Functions
Chapter 4 Review Exercises
For the following exercises, find the equation of the line using the point-slope formula.
- Passes through these two points: [latex]\,\left(-2,1\right)\text{,}\left(4,2\right).[/latex]
Show Solution
[latex]y=\frac{1}{6}x+\frac{4}{3}[/latex]
- Passes through the point [latex]\,\left(-3,4\right)\,[/latex] and has a slope of [latex]\,\frac{-1}{3}.[/latex]
- Passes through the point [latex]\,\left(-3,4\right)\,[/latex] and is parallel to the graph [latex]\,y=\frac{2}{3}x+5.[/latex]
Show Solution
[latex]y=\frac{2}{3}x+6[/latex]
- Passes through these two points: [latex]\,\left(5,1\right)\text{,}\left(5,7\right).[/latex]
Linear Functions
- Determine whether the algebraic equation is linear.[latex]\,2x+3y=7[/latex]
Show Solution
Yes
- Determine whether the algebraic equation is linear.[latex]\,6{x}^{2}-y=5[/latex]
- Determine whether the function is increasing or decreasing.
[latex]f\left(x\right)=7x-2[/latex]
Show Solution
Increasing
- Determine whether the function is increasing or decreasing.
[latex]g\left(x\right)=-x+2[/latex]
- Given each set of information, find a linear equation that satisfies the given conditions, if possible.
Passes through[latex]\,\left(\text{7},\text{5}\right)\,[/latex]and[latex]\,\left(\text{3},\text{17}\right)[/latex]
Show Solution
[latex]y=-\text{3}x+\text{26}[/latex]
- Given each set of information, find a linear equation that satisfies the given conditions, if possible.
x-intercept at[latex]\,\left(\text{6},0\right)\,[/latex]and y-intercept at[latex]\,\left(0,\text{1}0\right)[/latex]
- Find the slope of the line shown in the graph.
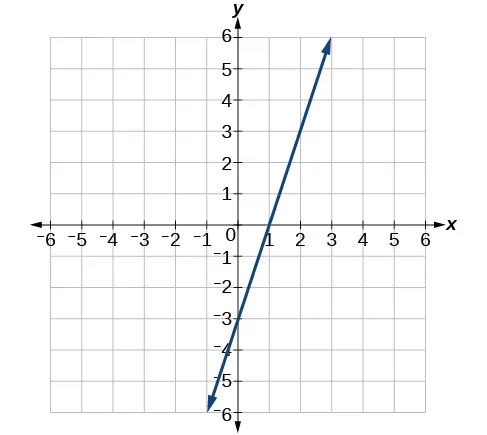
Show Solution
3
- Find the slope of the line graphed.
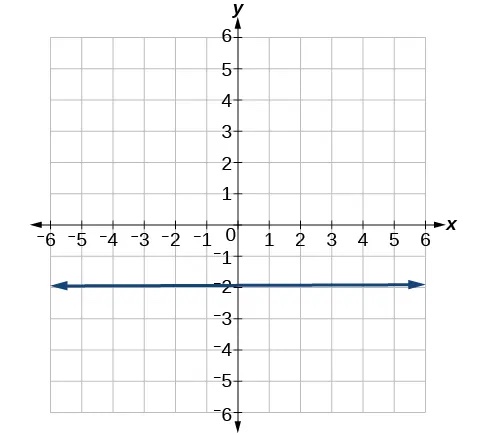
- Write an equation in slope-intercept form for the line shown.
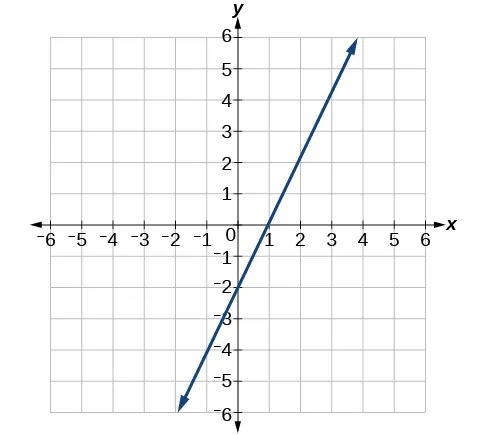
Show Solution
[latex]y=\text{2}x-\text{2}[/latex]
- Does the following table represent a linear function? If so, find the linear equation that models the data.
| x | –4 | 0 | 2 | 10 |
| g(x) | 18 | –2 | –12 | –52 |
- Does the following table represent a linear function? If so, find the linear equation that models the data.
| x | 6 | 8 | 12 | 26 |
| g(x) | –8 | –12 | –18 | –46 |
Show Solution
Not linear.
- On June 1st, a company has $4,000,000 profit. If the company then loses 150,000 dollars per day thereafter in the month of June, what is the company’s profit nthday after June 1st?
For the following exercises, determine whether the lines given by the equations below are parallel, perpendicular, or neither parallel nor perpendicular:
- [latex]\begin{array}{c}2x-6y=12\\ -x+3y=1\end{array}[/latex]
Show Solution
parallel
- [latex]\begin{array}{c}y=\frac{1}{3}x-2\\ 3x+y=-9\end{array}[/latex]
For the following exercises, find the x- and y- intercepts of the given equation
- [latex]7x+9y=-63[/latex]
Show Solution
[latex]\left(–9,0\right);\left(0,–7\right)[/latex]
- [latex]f\left(x\right)=2x-1[/latex]
For the following exercises, use the descriptions of the pairs of lines to find the slopes of Line 1 and Line 2. Is each pair of lines parallel, perpendicular, or neither?
- Line 1: Passes through[latex]\,\left(5,11\right)\,[/latex]and[latex]\,\left(10,1\right)[/latex]
Line 2: Passes through[latex]\,\left(-1,3\right)\,[/latex]and[latex]\,\left(-5,11\right)[/latex]
Show Solution
Line 1:[latex]\,m=-2;[/latex] Line 2:[latex]\,m=-2;[/latex]Parallel
- Line 1: Passes through[latex]\,\left(8,-10\right)\,[/latex]and[latex]\,\left(0,-26\right)[/latex]
Line 2: Passes through[latex]\,\left(2,5\right)\,[/latex]and[latex]\,\left(4,4\right)[/latex]
- Write an equation for a line perpendicular to[latex]\,f\left(x\right)=5x-1\,[/latex]and passing through the point (5, 20).
Show Solution
[latex]y=-0.2x+21[/latex]
- Find the equation of a line with a y- intercept of[latex]\,\left(0,2\right)\,[/latex]and slope[latex]\,-\frac{1}{2}.[/latex]
- Sketch a graph of the linear function[latex]\,f\left(t\right)=2t-5.[/latex]
Show Solution
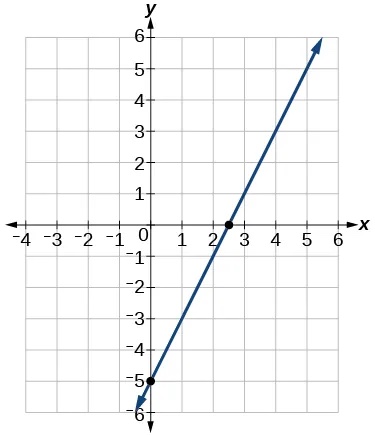
- Find the point of intersection for the 2 linear functions:[latex]\,\begin{array}{c}x=y+6\\ 2x-y=13\end{array}.[/latex]
- A car rental company offers two plans for renting a car.
Plan A: 25 dollars per day and 10 cents per mile
Plan B: 50 dollars per day with free unlimited mileage
How many miles would you need to drive for plan B to save you money?
Show Solution
More than 250
Modeling with Linear Functions
- Find the area of a triangle bounded by the y axis, the line[latex]\,f\left(x\right)=10-2x,[/latex] and the line perpendicular to[latex]\,f\,[/latex]that passes through the origin.
- A town’s population increases at a constant rate. In 2010 the population was 55,000. By 2012 the population had increased to 76,000. If this trend continues, predict the population in 2016.
Show Solution
118,000
- The number of people afflicted with the common cold in the winter months dropped steadily by 50 each year since 2004 until 2010. In 2004, 875 people were afflicted. Find the linear function that models the number of people afflicted with the common cold C as a function of the year,[latex]\,t.\,[/latex]When will no one be afflicted?
For the following exercises, use the graph in Figure 1 showing the profit,[latex]\,y,[/latex] in thousands of dollars, of a company in a given year,[latex]\,x,[/latex] where[latex]\,x\,[/latex]represents years since 1980.
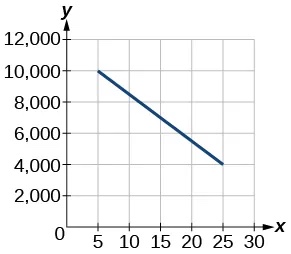
- Find the linear function y, where y depends on[latex]\,x,[/latex] the number of years since 1980.
Show Solution
[latex]y=-\text{3}00x+\text{11},\text{5}00[/latex]
- Find and interpret the y-intercept.
- For the following exercise, consider this scenario: In 2004, a school population was 1,700. By 2012 the population had grown to 2,500. Assume the population is changing linearly.
- How much did the population grow between the year 2004 and 2012?
- What is the average population growth per year?
- Find an equation for the population, P, of the school t years after 2004.
Show Solution
a) 800 b) 100 students per year c)[latex]\,P\left(t\right)=\text{1}00t+\text{17}00[/latex]
For the following exercises, consider this scenario: In 2000, the moose population in a park was measured to be 6,500. By 2010, the population was measured to be 12,500. Assume the population continues to change linearly.
- Find a formula for the moose population,[latex]\,P.[/latex]
- What does your model predict the moose population to be in 2020?
Show Solution
18,500
For the following exercises, consider this scenario: The median home values in subdivisions Pima Central and East Valley (adjusted for inflation) are shown below. Assume that the house values are changing linearly.
| Year | Pima Central | East Valley |
|---|---|---|
| 1970 | 32,000 | 120,250 |
| 2010 | 85,000 | 150,000 |
- In which subdivision have home values increased at a higher rate?
- If these trends were to continue, what would be the median home value in Pima Central in 2015?
Show Solution
$91,625
Systems of Linear Equations: Two Variables
For the following exercises, determine whether the ordered pair is a solution to the system of equations.
- [latex]\begin{array}{l}3x-y=4\\ x+4y=-3\,\end{array}[/latex]and[latex]\,\left(-1,1\right)[/latex]
Show Solution
No
- [latex]\begin{array}{l}6x-2y=24\\ -3x+3y=18\,\end{array}[/latex]and[latex]\,\left(9,15\right)[/latex]
For the following exercises, use substitution to solve the system of equations.
- [latex]\begin{array}{l}10x+5y=-5\hfill \\ \,\,\,3x-2y=-12\hfill \end{array}[/latex]
Show Solution
[latex]\left(-2,3\right)[/latex]
- [latex]\begin{array}{l}\frac{4}{7}x+\frac{1}{5}y=\frac{43}{70}\\ \frac{5}{6}x-\frac{1}{3}y=-\frac{2}{3}\end{array}[/latex]
- [latex]\begin{array}{l}5x+6y=14\\ 4x+8y=8\end{array}[/latex]
Show Solution
[latex]\left(4,-1\right)[/latex]
For the following exercises, use addition to solve the system of equations.
- [latex]\begin{array}{l}3x+2y=-7\\ 2x+4y=6\end{array}[/latex]
- [latex]\begin{array}{r}3x+4y=2\\ 9x+12y=3\end{array}[/latex]
Show Solution
No solutions exist.
- [latex]\begin{array}{l}8x+4y=2\\ 6x-5y=0.7\end{array}[/latex]
For the following exercises, write a system of equations to solve each problem. Solve the system of equations.
- A factory has a cost of production[latex]\,C\left(x\right)=150x+15\text{,}000\,[/latex]and a revenue function[latex]\,R\left(x\right)=200x.\,[/latex]What is the break-even point?
Show Solution
[latex]\left(300,60,000\right)[/latex]
- A performer charges[latex]\,C\left(x\right)=50x+10\text{,}000,\,[/latex]where[latex]\,x\,[/latex]is the total number of attendees at a show. The venue charges $75 per ticket. After how many people buy tickets does the venue break even, and what is the value of the total tickets sold at that point?
Show Solution
[latex]\left(400,30,000\right)[/latex]
Media Attributions
- Ch 4 Review #11 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- Ch 4 Review #12 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- Ch 4 Review #13 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- Ch 4 Review #25 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- Ch 4 Review Figure 1 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license

