Chapter 2 Equations and Inequalities
2.1 Linear Equations in One Variable
Learning Objectives
In this section you will:
- Solve equations in one variable.
- Solve a rational equation.
Caroline is a full-time college student planning a spring break vacation. To earn enough money for the trip, she has taken a part-time job at the local bank that pays $15.00/hr, and she opened a savings account with an initial deposit of $400 on January 15. She arranged for direct deposit of her payroll checks. If spring break begins March 20 and the trip will cost approximately $2,500, how many hours will she have to work to earn enough to pay for her vacation? If she can only work 4 hours per day, how many days per week will she have to work? How many weeks will it take? In this section, we will investigate problems like this and others, which generate graphs like the line in Figure 1.
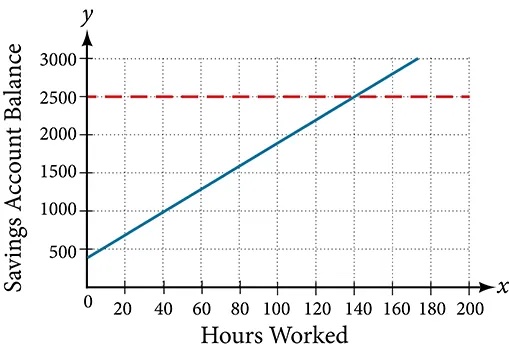
Solving Linear Equations in One Variable
A linear equation is an equation of a straight line, written in one variable. The only power of the variable is 1. Linear equations in one variable may take the form[latex]\,ax+b=0\,[/latex]and are solved using basic algebraic operations.
We begin by classifying linear equations in one variable as one of three types: identity, conditional, or inconsistent. An identity equation is true for all values of the variable. Here is an example of an identity equation.
The solution set consists of all values that make the equation true. For this equation, the solution set is all real numbers because any real number substituted for[latex]\,x\,[/latex]will make the equation true.
A conditional equation is true for only some values of the variable. For example, if we are to solve the equation[latex]\,5x+2=3x-6,[/latex] we have the following:
The solution set consists of one number:[latex]\,\left\{-4\right\}.\,[/latex]It is the only solution, and therefore, we have solved a conditional equation.
An inconsistent equation results in a false statement. For example, if we are to solve[latex]\,5x-15=5\left(x-4\right),[/latex] we have the following:
Indeed,[latex]\,-15\ne \,-20.\,[/latex]There is no solution because this is an inconsistent equation.
Solving linear equations in one variable involves the fundamental properties of equality and basic algebraic operations. A brief review of those operations follows.
Linear Equation in One Variable
A linear equation in one variable can be written in the form
where a and b are real numbers,[latex]\,a\ne 0.[/latex]
How To
Given a linear equation in one variable, use algebra to solve it.
The following steps are used to manipulate an equation and isolate the unknown variable, so that the last line reads[latex]\,x=[/latex]________ if x is the unknown. There is no set order, as the steps used depend on what is given:
- We may add, subtract, multiply, or divide an equation by a number or an expression as long as we do the same thing to both sides of the equal sign. Note that we cannot divide by zero.
- Apply the distributive property as needed:[latex]\,a\left(b+c\right)=ab+ac.[/latex]
- Isolate the variable on one side of the equation.
- When the variable is multiplied by a coefficient in the final stage, multiply both sides of the equation by the reciprocal of the coefficient.
Solving an Equation in One Variable
Solve the following equation:[latex]\,2x+7=19.[/latex]
Show Solution
This equation can be written in the form[latex]\,ax+b=0\,[/latex]by subtracting[latex]\,19\,[/latex]from both sides. However, we may proceed to solve the equation in its original form by performing algebraic operations.
The solution is 6
Try It
Solve the linear equation in one variable:[latex]\,2x+1=-9.[/latex]
Show Solution
[latex]x=-5[/latex]
Solving an Equation Algebraically When the Variable Appears on Both Sides
Solve the following equation: [latex]4(x-3)+12=15-5(x+6)[/latex]
Show Solution
Apply standard algebraic properties.
| [latex]4(x-3)+12=15-5(x+6)[/latex] | |
| [latex]4x-12+12=15-5x-30[/latex] | Apply the distributive property. |
| [latex]4x=-15-5x[/latex] | Combine like terms. |
| [latex]9x=-15[/latex] | Place x -terms on one side and simplify. |
| [latex]x=- \dfrac{15}{9}[/latex] | Multiply both sides by [latex]\dfrac{1}{9}[/latex], the reciprocal of 9. |
| [latex]x=- \dfrac{5}{3}[/latex] | Simplify the fraction. |
Analysis
This problem requires the distributive property to be applied twice, and then the properties of algebra are used to reach the final line,[latex]\,x=-\frac{5}{3}.[/latex]
Try It
Solve the equation in one variable:[latex]\,-2\left(3x-1\right)+x=14-x.[/latex]
Show Solution
[latex]x=-3[/latex]
Solving a Rational Equation
In this section, we look at rational equations that, after some manipulation, result in a linear equation. If an equation contains at least one rational expression, it is considered a rational equation.
Recall that a rational number is the ratio of two numbers, such as[latex]\,\frac{2}{3}\,[/latex]or[latex]\,\frac{7}{2}.\,[/latex]A rational expression is the ratio, or quotient, of two polynomials. Here are three examples.
Rational equations have a variable in the denominator in at least one of the terms.
Our goal is to perform algebraic operations so that the variables appear in the numerator. In fact, we will eliminate all denominators by multiplying both sides of the equation by the least common denominator (LCD).
Finding the LCD is identifying an expression that contains the highest power of all of the factors in all of the denominators. We do this because when the equation is multiplied by the LCD, the common factors in the LCD and in each denominator will equal one and will cancel out.
Solving a Rational Equation
Solve the rational equation:[latex]\,\frac{7}{2x}-\frac{5}{3x}=\frac{22}{3}.[/latex]
Show Solution
We have three denominators;[latex]\,2x,3x,[/latex] and [latex]3[/latex]. The LCD must contain[latex]\,2x,3x,[/latex]and [latex]3[/latex]. An LCD of[latex]\,6x\,[/latex]contains all three denominators. In other words, each denominator can be divided evenly into the LCD.
| [latex](6x) \left(\dfrac{7}{2x}-\dfrac{5}{3x} \right)[/latex] | = [latex] \left(\dfrac{22}{3} \right)(6x)[/latex] | Multiply both sides of the equation by the LCD[latex]\,6x.[/latex] |
| [latex](6x) \left(\dfrac{7}{2x} \right)-(6x) \left(\dfrac{5}{3x} \right)[/latex] | = [latex] \left(\dfrac{22}{3} \right)(6x)[/latex] | Use the distributive property. |
| [latex](\cancel{6x}) \left(\dfrac{7}{\cancel{2x}} \right)-(\cancel{6x}) \left(\dfrac{5}{\cancel{3x}} \right)[/latex] | = [latex] \left(\dfrac{22}{\cancel{3}} \right)(\cancel{6} x)[/latex] | Cancel out the common factors. |
| [latex]3 (7) - 2 (5)[/latex] | = [latex]22(2x)[/latex] | Multiply the remaining factors by each numerator. |
| [latex]21 - 10[/latex] | = [latex]44x[/latex] | Simplify. |
| [latex]11[/latex] | = [latex]44x[/latex] | Divide. |
| [latex]\dfrac{11}{44}[/latex] | = [latex]x[/latex] | |
| [latex]\dfrac{1}{4}[/latex] | = [latex]x[/latex] | Simplify. |
A common mistake made when solving rational equations involves finding the LCD when one of the denominators is a binomial—two terms added or subtracted—such as[latex]\,\left(x+1\right).\,[/latex]Always consider a binomial as an individual factor—the terms cannot be separated. For example, suppose a problem has three terms and the denominators are[latex]\,x,[/latex][latex]x-1,[/latex] and[latex]\,3x-3.\,[/latex]First, factor all denominators. We then have[latex]\,x,[/latex][latex]\left(x-1\right),[/latex]and[latex]\,3\left(x-1\right)\,[/latex]as the denominators. (Note the parentheses placed around the second denominator.) Only the last two denominators have a common factor of[latex]\,\left(x-1\right).\,[/latex]The[latex]\,x\,[/latex]in the first denominator is separate from the[latex]\,x\,[/latex]in the[latex]\,\left(x-1\right)\,[/latex]denominators. An effective way to remember this is to write factored and binomial denominators in parentheses, and consider each parentheses as a separate unit or a separate factor. The LCD in this instance is found by multiplying together the[latex]\,x,[/latex] one factor of[latex]\,\left(x-1\right),[/latex] and the 3. Thus, the LCD is the following:
So, both sides of the equation would be multiplied by[latex]\,3x\left(x-1\right).\,[/latex]Leave the LCD in factored form, as this makes it easier to see how each denominator in the problem cancels out.
Another example is a problem with two denominators, such as[latex]\,x\,[/latex]and[latex]\,{x}^{2}+2x.\,[/latex]Once the second denominator is factored as[latex]\,{x}^{2}+2x=x\left(x+2\right),[/latex] there is a common factor of x in both denominators and the LCD is[latex]\,x\left(x+2\right).[/latex]
Sometimes we have a rational equation in the form of a proportion—that is, when one fraction equals another fraction and there are no other terms in the equation.
We can use another method of solving the equation without finding the LCD: cross-multiplication. We multiply terms by crossing over the equal sign.
![]()
Multiply[latex]\,a\left(d\right)\,[/latex]and[latex]\,b\left(c\right),[/latex] which results in[latex]\,ad=bc.[/latex]
Any solution that makes a denominator in the original expression equal zero must be excluded from the possibilities.
Rational Equations
A rational equation contains at least one rational expression where the variable appears in at least one of the denominators.
How To
Given a rational equation, solve it.
- Factor all denominators in the equation.
- Find and exclude values that set each denominator equal to zero.
- Find the LCD.
- Multiply the whole equation by the LCD. If the LCD is correct, there will be no denominators left.
- Solve the remaining equation.
- Make sure to check solutions back in the original equations to avoid a solution producing zero in a denominator
Solving a Rational Equation without Factoring
Solve the following rational equation:
Show Solution
We have three denominators:[latex]\,x,[/latex][latex]2,[/latex]and[latex]\,2x.\,[/latex]No factoring is required. The product of the first two denominators is equal to the third denominator, so, the LCD is[latex]\,2x.\,[/latex]Only one value is excluded from a solution set, 0.[latex][/latex] Next, multiply the whole equation (both sides of the equal sign) by[latex]\,2x.[/latex]
| [latex]2x\left(\frac{2}{x}-\frac{3}{2}\right)[/latex] | [latex]= \left(\frac{7}{2x}\right)2x[/latex] | |
| [latex]2 x\left(\frac{2}{x}\right)-2x\left(\frac{3}{2}\right)[/latex] | [latex]=\left(\frac{7}{2x}\right)2x[/latex] | Distribute [latex]2x[/latex] |
| [latex]2 \cancel{x}\left(\frac{2}{\cancel{x}}\right)-2x\left(\frac{3}{2}\right)[/latex] | [latex]=\left(\frac{7}{\cancel{2x}}\right)\cancel{2x}[/latex] | Denominators cancel out. |
| [latex]2\left(2\right)-3x[/latex] | [latex]=7[/latex] | Mulitply. |
| [latex]4-3x[/latex] | [latex]=7[/latex] | |
| [latex]-3x[/latex] | [latex]=3[/latex] | |
| [latex]x[/latex] | [latex]=-1[/latex] | |
| or [latex]{-1}[/latex] |
The proposed solution is −1,[latex][/latex] which is not an excluded value, so the solution set contains one number,[latex]\,x=-1,[/latex]or[latex]\,\left\{-1\right\}\,[/latex]written in set notation.
Try It
Solve the rational equation:[latex]\,\frac{2}{3x}=\frac{1}{4}-\frac{1}{6x}.[/latex]
Show Solution
[latex]x=\frac{10}{3}[/latex]
Solving a Rational Equation by Factoring the Denominator
Solve the following rational equation:[latex]\,\frac{1}{x}=\frac{1}{10}-\frac{3}{4x}.[/latex]
Show Solution
First find the common denominator. The three denominators in factored form are[latex]\,x,10=2\cdot 5,[/latex] and[latex]\,4x=2\cdot 2\cdot x.\,[/latex]The smallest expression that is divisible by each one of the denominators is[latex]\,20x.\,[/latex]Only[latex]\,x=0\,[/latex]is an excluded value. Multiply the whole equation by[latex]\,20x.[/latex]
The solution is[latex]\,\frac{35}{2}.[/latex]
Try It
Solve the rational equation:[latex]\,-\frac{5}{2x}+\frac{3}{4x}=-\frac{7}{4}.[/latex]
Show Solution
[latex]x=1[/latex]
Solving Rational Equations with a Binomial in the Denominator
Solve the following rational equations and state the excluded values:
- [latex]\frac{3}{x-6}=\frac{5}{x}[/latex]
- [latex]\frac{x}{x-3}=\frac{5}{x-3}-\frac{1}{2}[/latex]
- [latex]\frac{x}{x-2}=\frac{5}{x-2}-\frac{1}{2}[/latex]
Show Solution
- The denominators[latex]\,x\,[/latex]and[latex]\,x-6\,[/latex]have nothing in common. Therefore, the LCD is the product[latex]\,x\left(x-6\right).\,[/latex]However, for this problem, we can cross-multiply.
[latex]\begin{array}{cccc}\hfill \frac{3}{x-6}& =& \frac{5}{x}\hfill & \\ \hfill 3x& =& 5\left(x-6\right)\hfill & \phantom{\rule{2em}{0ex}}\text{Distribute}\text{.}\hfill \\ \hfill 3x& =& 5x-30\hfill & \\ \hfill -2x& =& -30\hfill & \\ \hfill x& =& 15\hfill & \end{array}[/latex]
The solution is 15.[latex][/latex] The excluded values are [latex]6[/latex] and [latex]0.[/latex]
- The LCD is[latex]\,2\left(x-3\right).\,[/latex]Multiply both sides of the equation by[latex]\,2\left(x-3\right).[/latex]
[latex]\begin{array}{ccc}\hfill 2\left(x-3\right)\left[\frac{x}{x-3}\right]& =& \left[\frac{5}{x-3}-\frac{1}{2}\right]2\left(x-3\right)\hfill \\ \hfill \frac{2 \cancel{(x-3)}x}{\cancel{(x-3)}}& =& \frac{2 \cancel{(x-3)} 5}{\cancel{(x-3)}}-\frac{\cancel{2}\left(x-3\right)}{\cancel{2}}\hfill \\ \hfill 2x& =& 10-\left(x-3\right)\hfill \\ \hfill 2x& =& 10-x+3\hfill \\ \hfill 2x& =& 13-x\hfill \\ \hfill 3x& =& 13\hfill \\ \hfill x& =& \frac{13}{3}\hfill \end{array}[/latex]
The solution is[latex]\,\frac{13}{3}.\,[/latex]The excluded value is [latex]3.[/latex]
- The least common denominator is[latex]\,2\left(x-2\right).\,[/latex]Multiply both sides of the equation by[latex]\,x\left(x-2\right).[/latex]
[latex]\begin{array}{ccc}\hfill 2\left(x-2\right)\left[\frac{x}{x-2}\right]& =& \left[\frac{5}{x-2}-\frac{1}{2}\right]2\left(x-2\right)\hfill \\ \hfill 2x& =& 10-\left(x-2\right)\hfill \\ \hfill 2x& =& 12-x\hfill \\ \hfill 3x& =& 12\hfill \\ \hfill x& =& 4\hfill \end{array}[/latex]
The solution is 4. The excluded value is [latex]2.[/latex]
Try It
Solve[latex]\,\frac{-3}{2x+1}=\frac{4}{3x+1}.\,[/latex]State the excluded values.
Show Solution
[latex]x=-\frac{7}{17}.\,[/latex]Excluded values are[latex]\,x=-\frac{1}{2}\,[/latex]and[latex]\,x=-\frac{1}{3}.[/latex]
Solving a Rational Equation with Factored Denominators and Stating Excluded Values
Solve the rational equation after factoring the denominators:[latex]\,\frac{2}{x+1}-\frac{1}{x-1}=\frac{2x}{{x}^{2}-1}.\,[/latex]State the excluded values.
Show Solution
We must factor the denominator[latex]\,{x}^{2}-1.\,[/latex]We recognize this as the difference of squares, and factor it as[latex]\,\left(x-1\right)\left(x+1\right).\,[/latex]Thus, the LCD that contains each denominator is[latex]\,\left(x-1\right)\left(x+1\right).\,[/latex]Multiply the whole equation by the LCD, cancel out the denominators, and solve the remaining equation.
The solution is [latex]\,-3.\,[/latex]The excluded values are [latex]\,1\,[/latex] and [latex]\,-1.[/latex]
Try It
Solve the rational equation:[latex]\,\frac{2}{x-2}+\frac{1}{x+1}=\frac{1}{{x}^{2}-x-2}.[/latex]
Show Solution
[latex]x=\frac{1}{3}[/latex]
Key Concepts
- We can solve linear equations in one variable in the form[latex]\,ax+b=0\,[/latex]using standard algebraic properties.
- A rational expression is a quotient of two polynomials. We use the LCD to clear the fractions from an equation.
- All solutions to a rational equation should be verified within the original equation to avoid an undefined term, or zero in the denominator.
Section Exercises
Verbal
- What does it mean when we say that a linear equation is inconsistent?
- When solving the following equation: [latex]\frac{2}{x-5}=\frac{4}{x+1}[/latex] explain why we must exclude[latex]\,x=5\,[/latex]and[latex]\,x=-1\,[/latex]as possible solutions from the solution set.
Show Solution
If we insert either value into the equation, they make an expression in the equation undefined (zero in the denominator).
Algebraic
For the following exercises, solve the equation for[latex]\,x.[/latex]
- [latex]7x+2=3x-9[/latex]
- [latex]4x-3=5[/latex]
Show Solution to [latex]4x-3=5[/latex]
[latex]x=2[/latex]
- [latex]3\left(x+2\right)-12=5\left(x+1\right)[/latex]
- [latex]12-5\left(x+3\right)=2x-5[/latex]
Show Solution
[latex]x=\frac{2}{7}[/latex]
- [latex]\frac{1}{2}-\frac{1}{3}x=\frac{4}{3}[/latex]
- [latex]\frac{x}{3}-\frac{3}{4}=\frac{2x+3}{12}[/latex]
Show Solution
[latex]x=6[/latex]
- [latex]\frac{2}{3}x+\frac{1}{2}=\frac{31}{6}[/latex]
- [latex]3\left(2x-1\right)+x=5x+3[/latex]
Show Solution
[latex]x=3[/latex]
- [latex]\frac{2x}{3}-\frac{3}{4}=\frac{x}{6}+\frac{21}{4}[/latex]
- [latex]\frac{x+2}{4}-\frac{x-1}{3}=2[/latex]
Show Solution
[latex]x=-14[/latex]
For the following exercises, solve each rational equation for[latex]\,x.\,[/latex]State all x-values that are excluded from the solution set.
- [latex]\frac{3}{x}-\frac{1}{3}=\frac{1}{6}[/latex]
- [latex]2-\frac{3}{x+4}=\frac{x+2}{x+4}[/latex]
Show Solution
[latex]x\ne -4;[/latex][latex]x=-3[/latex]
- [latex]\frac{3}{x-2}=\frac{1}{x-1}+\frac{7}{\left(x-1\right)\left(x-2\right)}[/latex]
- [latex]\frac{3x}{x-1}+2=\frac{3}{x-1}[/latex]
Show Solution
[latex]x\ne 1;[/latex]when we solve this we get[latex]\,x=1,[/latex]which is excluded, therefore NO solution
- [latex]\frac{5}{x+1}+\frac{1}{x-3}=\frac{-6}{{x}^{2}-2x-3}[/latex]
- [latex]\frac{1}{x}=\frac{1}{5}+\frac{3}{2x}[/latex]
Show Solution
[latex]x\ne 0;[/latex][latex]x=\frac{-5}{2}[/latex]
Glossary
- conditional equation
- an equation that is true for some values of the variable
- identity equation
- an equation that is true for all values of the variable
- inconsistent equation
- an equation producing a false result
- linear equation
- an algebraic equation in which each term is either a constant or the product of a constant and the first power of a variable
- solution set
- the set of all solutions to an equation
- rational equation
- an equation consisting of a fraction of polynomials
Media Attributions
- 2.1 Figure 1 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 2.1 Proportion Graphic © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license

