Chapter 6 Review Exercises

Cynthia Singleton; Ginny Bradley; Karen Perilloux; Prakash Ghimire

Chapter 6 Exponential and Logarithmic Functions

Chapter 6 Review Exercises

Exponential Functions

Determine whether the function $y = 156 {(0.825)}^{t}$ represents exponential growth, exponential decay, or neither. Explain

Show Solution

exponential decay; The growth factor, $0.825,$ is between $0$ and $1.$

The population of a herd of deer is represented by the function $A (t) = 205 {(1.13)}^{t},$ where $t$ is given in years. To the nearest whole number, what will the herd population be after $6$ years?

Find an exponential equation that passes through the points $(2, 2 .25)$ and $(5, 60.75) .$

Show Solution

$y = 0.25 {(3)}^{x}$

Determine whether the following table could represent a function that is linear, exponential, or neither. If it appears to be exponential, find a function that passes through the points.

x	1	2	3	4
*f(x)*	3	0.9	0.27	0.081

A retirement account is opened with an initial deposit of $8,500 and earns $8.12$ % interest compounded monthly. What will the account be worth in $20$ years?

Show Solution

$$ 42, 888.18$

Hsu-Mei wants to save $5,000 for a down payment on a car. To the nearest dollar, how much will she need to invest in an account now with $7.5$ % APR, compounded daily, in order to reach her goal in $3$ years?

Does the equation $y = 2.294 e^{- 0.654 t}$ represent continuous growth, continuous decay, or neither? Explain.

Show Solution

continuous decay; the growth rate is negative.

Suppose an investment account is opened with an initial deposit of $$10,500$ earning $6.25$ % interest, compounded continuously. How much will the account be worth after $25$ years?

Graphs of Exponential Functions

Graph the function $f (x) = 3.5 {(2)}^{x} .$ State the domain and range and give the y-intercept.

Show Solution

domain: all real numbers; range: all real numbers strictly greater than zero; y-intercept: (0, 3.5);

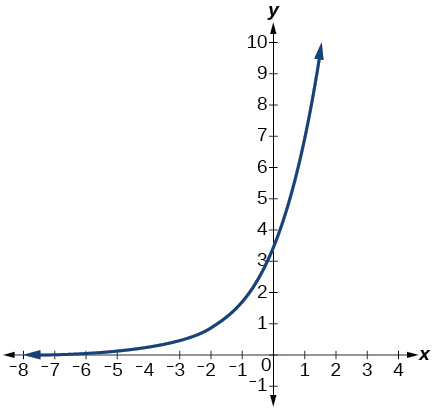
Graph of f(x)=3.5(2^x)

Graph the function $f (x) = 4 {(\frac{1}{8})}^{x}$ and its reflection about the y-axis on the same axes, and give the y-intercept.

The graph of $f (x) = {6.5}^{x}$ is reflected about the y-axis and stretched vertically by a factor of $7.$ What is the equation of the new function, $g (x) ?$ State its y-intercept, domain, and range.

Show Solution

$g (x) = 7 {(6.5)}^{- x};$ y-intercept: $(0, 7);$ Domain: all real numbers; Range: all real numbers greater than $0.$

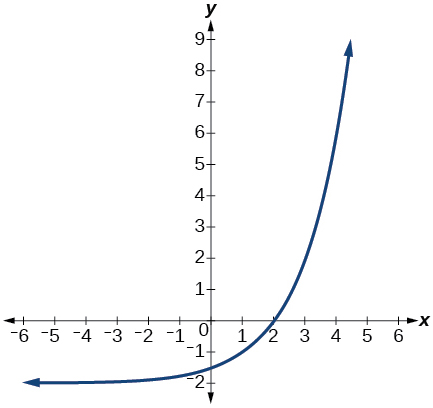
The graph below shows transformations of the graph of $f (x) = 2^{x} .$ What is the equation for the transformation?

Graph of f(x)=2^x

Logarithmic Functions

Rewrite $\log_{17} (4913) = x$ as an equivalent exponential equation.

Show Solution

$17^{x} = 4913$

Rewrite $\ln (s) = t$ as an equivalent exponential equation.

Rewrite $a^{- \frac{2}{5}} = b$ as an equivalent logarithmic equation.

Show Solution

$\log_{a} b = - \frac{2}{5}$

Rewrite $e^{- 3.5} = h$ as an equivalent logarithmic equation.

Solve for x if $\log_{64} (x) = \frac{1}{3}$ by converting to exponential form.

Show Solution

$x = 64^{\frac{1}{3}} = 4$

Evaluate $\log_{5} (\frac{1}{125})$ without using a calculator.

Evaluate $\log (0 .000001)$ without using a calculator.

Show Solution

$\log (0 .000001) = - 6$

Evaluate $\log (4.005)$ using a calculator. Round to the nearest thousandth.

Evaluate $\ln (e^{- 0.8648})$ without using a calculator.

Show Solution

$\ln (e^{- 0.8648}) = - 0.8648$

Evaluate $\ln (\sqrt[3]{18})$ using a calculator. Round to the nearest thousandth.

Graphs of Logarithmic Functions

Graph the function $g (x) = \log (7 x + 21) - 4.$

Show Solution

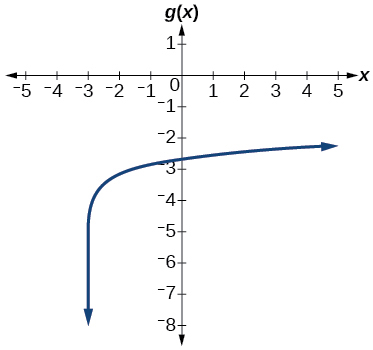
Graph of g(x)=log(7x+21)-4.

Graph the function $h (x) = 2 \ln (9 - 3 x) + 1.$

State the domain, vertical asymptote, and end behavior of the function $g (x) = \ln (4 x + 20) - 17.$

Show Solution

Domain: $x > - 5;$ Vertical asymptote: $x = - 5;$ End behavior: as $x \to - 5^{+}, f (x) \to - \infty$ and as $x \to \infty, f (x) \to \infty .$

Logarithmic Properties

Rewrite $\ln (7 r \cdot 11 s t)$ in expanded form.

Rewrite $\log_{8} (x) + \log_{8} (5) + \log_{8} (y) + \log_{8} (13)$ in compact form.

Show Solution

${log}_{8} (65 x y)$

Rewrite $\log_{m} (\frac{67}{83})$ in expanded form.

Rewrite $\ln (z) - \ln (x) - \ln (y)$ in compact form.

Show Solution

$\ln (\frac{z}{x y})$

Rewrite $\ln (\frac{1}{x^{5}})$ as a product.

Rewrite $- \log_{y} (\frac{1}{12})$ as a single logarithm.

Show Solution

${log}_{y} (12)$

Use properties of logarithms to expand $\log (\frac{r^{2} s^{11}}{t^{14}}) .$

Use properties of logarithms to expand $\ln (2 b \sqrt{\frac{b + 1}{b - 1}}) .$

Show Solution

$\ln (2) + \ln (b) + \frac{\ln (b + 1) - \ln (b - 1)}{2}$

Condense the expression $5 \ln (b) + \ln (c) + \frac{\ln (4 - a)}{2}$ to a single logarithm.

Condense the expression $3 \log_{7} v + 6 \log_{7} w - \frac{\log_{7} u}{3}$ to a single logarithm.

Show Solution

$\log_{7} (\frac{v^{3} w^{6}}{\sqrt[3]{u}})$

Rewrite $\log_{3} (12.75)$ to base $e .$

Rewrite $5^{12 x - 17} = 125$ as a logarithm. Then apply the change of base formula to solve for $x$ using the common log. Round to the nearest thousandth.

Show Solution

$x = \frac{\frac{\log (125)}{\log (5)} + 17}{12} = \frac{5}{3}$

Exponential and Logarithmic Equations

Solve $216^{3 x} \cdot 216^{x} = 36^{3 x + 2}$ by rewriting each side with a common base.

Solve $\frac{125}{{(\frac{1}{625})}^{- x - 3}} = 5^{3}$ by rewriting each side with a common base.

Show Solution

$x = - 3$

Use logarithms to find the exact solution for $7 \cdot 17^{- 9 x} - 7 = 49.$ If there is no solution, write no solution.

Use logarithms to find the exact solution for $3 e^{6 n - 2} + 1 = - 60.$ If there is no solution, write no solution.

Show Solution

no solution

Find the exact solution for $5 e^{3 x} - 4 = 6$ . If there is no solution, write no solution.

Find the exact solution for $2 e^{5 x - 2} - 9 = - 56.$ If there is no solution, write no solution.

Show Solution

no solution

Find the exact solution for $5^{2 x - 3} = 7^{x + 1} .$ If there is no solution, write no solution.

Find the exact solution for $e^{2 x} - e^{x} - 110 = 0.$ If there is no solution, write no solution.

Show Solution

$x = \ln (11)$

Use the definition of a logarithm to solve. $- 5 \log_{7} (10 n) = 5.$

47. Use the definition of a logarithm to find the exact solution for $9 + 6 \ln (a + 3) = 33.$

Show Solution

$a = e^{4} - 3$

Use the one-to-one property of logarithms to find an exact solution for $\log_{8} (7) + \log_{8} (- 4 x) = \log_{8} (5) .$ If there is no solution, write no solution.

Use the one-to-one property of logarithms to find an exact solution for $\ln (5) + \ln (5 x^{2} - 5) = \ln (56) .$ If there is no solution, write no solution.

Show Solution

$x = \pm \frac{9}{5}$

The formula for measuring sound intensity in decibels $D$ is defined by the equation $D = 10 \log (\frac{I}{I_{0}}),$ where $I$ is the intensity of the sound in watts per square meter and $I_{0} = 10^{- 12}$ is the lowest level of sound that the average person can hear. How many decibels are emitted from a large orchestra with a sound intensity of $6.3 \cdot 10^{- 3}$ watts per square meter?

The population of a city is modeled by the equation $P (t) = 256, 114 e^{0.25 t}$ where $t$ is measured in years. If the city continues to grow at this rate, how many years will it take for the population to reach one million?

Show Solution

about $5.45$ years

Find the inverse function $f^{- 1}$ for the exponential function $f (x) = 2 \cdot e^{x + 1} - 5.$

Find the inverse function $f^{- 1}$ for the logarithmic function $f (x) = 0.25 \cdot \log_{2} (x^{3} + 1) .$

Show Solution

$f^{- 1} (x) = \sqrt[3]{2^{4 x} - 1}$

Exponential and Logarithmic Models

For the following exercises, use this scenario: A doctor prescribes $300$ milligrams of a therapeutic drug that decays by about $17$ % each hour.

To the nearest minute, what is the half-life of the drug?

Write an exponential model representing the amount of the drug remaining in the patient’s system after $t$ hours. Then use the formula to find the amount of the drug that would remain in the patient’s system after $24$ hours. Round to the nearest hundredth of a gram.

Show Solution

$f (t) = 300 {(0.83)}^{t}; f (24) \approx 3.43 g$

For the following exercises, use this scenario: A soup with an internal temperature of $350°$ Fahrenheit was taken off the stove to cool in a $71°F$ room. After fifteen minutes, the internal temperature of the soup was $175°F .$

Use Newton’s Law of Cooling to write a formula that models this situation.

How many minutes will it take the soup to cool to $85°F?$

Show Solution

about $45$ minutes

For the following exercises, use this scenario: The equation $N (t) = \frac{1200}{1 + 199 e^{- 0.625 t}}$ models the number of people in a school who have heard a rumor after $t$ days.

How many people started the rumor?

To the nearest tenth, how many days will it be before the rumor spreads to half the carrying capacity?

Show Solution

about $8.5$ days

What is the carrying capacity?

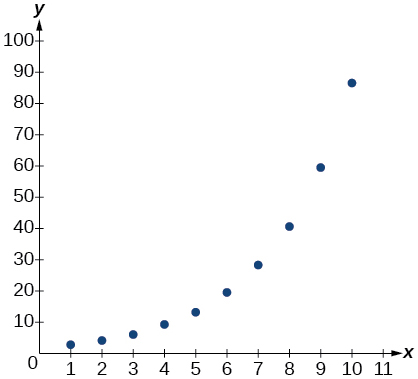
For the following exercises, enter the data from each table into a graphing calculator and graph the resulting scatter plots. Determine whether the data from the table would likely represent a function that is linear, exponential, or logarithmic.

x	f(x)
1	3.05
2	4.42
3	6.4
4	9.28
5	13.46
6	19.52
7	28.3
8	41.04
9	50.5
10	86.28

Show Solution

exponential

Graph of the table’s values.

x	*f(x)*
0.5	18.05
1	17
3	15.33
5	14.55
7	14.04
10	13.5
12	13.22
13	13.1
15	12.88
17	12.69
20	12.45

Find a formula for an exponential equation that goes through the points $(- 2, 100)$ and $(0, 4) .$ Then express the formula as an equivalent equation with base e.

Show Solution

$y = 4 {(0.2)}^{x};$ $y = 4 e^{-1 .609438 x}$

Media Attributions

License

Icon for the Creative Commons Attribution 4.0 International License

Exponential Functions

Graphs of Exponential Functions

Logarithmic Functions

Graphs of Logarithmic Functions

Logarithmic Properties

Exponential and Logarithmic Equations

Exponential and Logarithmic Models

Media Attributions

License

Share This Book