Chapter 4 Linear Functions

4.2 Linear Functions

Learning Objectives

In this section, you will:

  • Represent a linear function.
  • Determine whether a linear function is increasing, decreasing, or constant.
  • Interpret slope as a rate of change.
  • Write and interpret an equation for a linear function.
  • Graph linear functions.
Front view of a subway train, the maglev train.
Figure 1. Shanghai MagLev Train (credit: “kanegen”/Flickr)

Just as with the growth of a bamboo plant, there are many situations that involve constant change over time. Consider, for example, the first commercial maglev train in the world, the Shanghai MagLev Train ( Figure 1). It carries passengers comfortably for a 30-kilometer trip from the airport to the subway station in only eight minutes [1].

Suppose a maglev train travels a long distance, and maintains a constant speed of 83 meters per second for a period of time once it is 250 meters from the station. How can we analyze the train’s distance from the station as a function of time? In this section, we will investigate a kind of function that is useful for this purpose, and use it to investigate real-world situations such as the train’s distance from the station at a given point in time.

Representing Linear Functions

The function describing the train’s motion is a linear function, which is defined as a function with a constant rate of change. This is a polynomial of degree 1. There are several ways to represent a linear function, including word form, function notation, tabular form, and graphical form. We will describe the train’s motion as a function using each method.

Representing a Linear Function in Word Form

Let’s begin by describing the linear function in words. For the train problem we just considered, the following word sentence may be used to describe the function relationship.

  • The train’s distance from the station is a function of the time during which the train moves at a constant speed plus its original distance from the station when it began moving at constant speed.

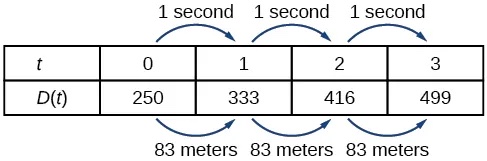
The speed is the rate of change. Recall that a rate of change is a measure of how quickly the dependent variable changes with respect to the independent variable. The rate of change for this example is constant, which means that it is the same for each input value. As the time (input) increases by 1 second, the corresponding distance (output) increases by 83 meters. The train began moving at this constant speed at a distance of 250 meters from the station.

Representing a Linear Function in Function Notation

Another approach to representing linear functions is by using function notation. One example of function notation is an equation written in the slope-intercept form of a line, where[latex]\,x\,[/latex]is the input value,[latex]\,m\,[/latex]is the rate of change, and[latex]\,b\,[/latex]is the initial value of the dependent variable.

[latex]\begin{array}{cc}\text{Equation form}\phantom{\rule{2em}{0ex}}\hfill & y=mx+b\hfill \\ \text{Function notation}\phantom{\rule{2em}{0ex}}\hfill & f\left(x\right)=mx+b\hfill \end{array}[/latex]

In the example of the train, we might use the notation[latex]\,D\left(t\right)\,[/latex]where the total distance[latex]\,D\,[/latex]is a function of the time[latex]\,t.\,[/latex]The rate,[latex]\,m,\,[/latex]is 83 meters per second. The initial value of the dependent variable[latex]\,b\,[/latex]is the original distance from the station, 250 meters. We can write a generalized equation to represent the motion of the train.

[latex]D\left(t\right)=83t+250[/latex]

Representing a Linear Function in Tabular Form

A third method of representing a linear function is through the use of a table. The relationship between the distance from the station and the time is represented in Figure 2. From the table, we can see that the distance changes by 83 meters for every 1 second increase in time.

Table with the first row, labeled t, containing the seconds from 0, 1, 2, 3, and with the second row, labeled D (t), containing the meters 250, 333, 416, and 499. Each value in the first row increases by 1 second, and each value in the second row increases by 83 meters.
Figure 2 Tabular representation of the function 𝐷 showing selected input and output values

Can the input in the previous example be any real number?

No. The input represents time, so while nonnegative rational and irrational numbers are possible, negative real numbers are not possible for this example. The input consists of non-negative real numbers.

Representing a Linear Function in Graphical Form

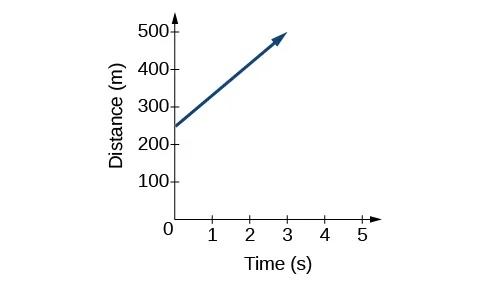
Another way to represent linear functions is visually, using a graph. We can use the function relationship from above,[latex]\,D\left(t\right)=83t+250,\,[/latex]to draw a graph as represented in Figure 3. Notice the graph is a line. When we plot a linear function, the graph is always a line.

The rate of change, which is constant, determines the slant, or slope of the line. The point at which the input value is zero is the vertical intercept, or y-intercept, of the line. We can see from the graph that the y-intercept in the train example we just saw is[latex]\,\left(0,250\right)\,[/latex]and represents the distance of the train from the station when it began moving at a constant speed.

This is a graph with y-axis labeled “Distance (m)” and x-axis labeled “Time (s).” The x-axis spans from 0 to 5 and is marked in increments of one. The y-axis spans from 0 to 500 and is marked in increments of one hundred. The graph shows an increasing function. As time increases, distance also increases. The line is graphed along the points (0, 250) and (1, 333)
Figure 3 The graph of 𝐷(𝑡)=83𝑡+250 . Graphs of linear functions are lines because the rate of change is constant.

Notice that the graph of the train example is restricted, but this is not always the case. Consider the graph of the line[latex]\,f\left(x\right)=2x+1.\,[/latex]
Ask yourself what numbers can be input to the function. In other words, what is the domain of the function? The domain is composed of all real numbers because any number may be doubled, and then have one added to the product.

Linear Function

A linear function is a function whose graph is a line. Linear functions can be written in the slope-intercept form of a line

[latex]f\left(x\right)=mx+b[/latex]

where[latex]\,b\,[/latex]is the initial or starting value of the function (when input[latex]\,x=0\,[/latex]), and[latex]\,m\,[/latex]is the constant rate of change, or slope of the function. The y-intercept is at[latex]\,\left(0,b\right).[/latex]

Using a Linear Function to Find the Pressure on a Diver

The pressure,[latex]\,P,[/latex] in pounds per square inch (PSI) on the diver in Figure 4 depends on her depth below the water surface,[latex]\,d,[/latex] in feet. This relationship may be modeled by the equation[latex]\,P\left(d\right)=0.434d+14.696.\,[/latex]Restate this function in words.

This figure shows a scuba diver.
Figure 4 (credit: Ilse Reijs and Jan-Noud Hutten)

 

Show Solution

To restate the function in words, we need to describe each part of the equation. The pressure as a function of depth equals four hundred thirty-four thousandths times depth plus fourteen and six hundred ninety-six thousandths.

Analysis

The initial value, 14.696, is the pressure in PSI on the diver at a depth of 0 feet, which is the surface of the water. The rate of change, or slope, is 0.434 PSI per foot. This tells us that the pressure on the diver increases 0.434 PSI for each foot her depth increases.

Determining Whether a Linear Function Is Increasing, Decreasing, or Constant

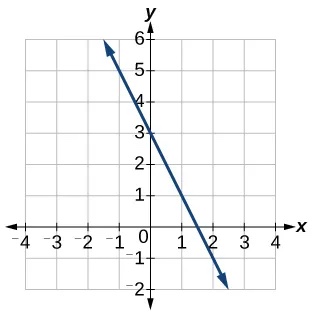
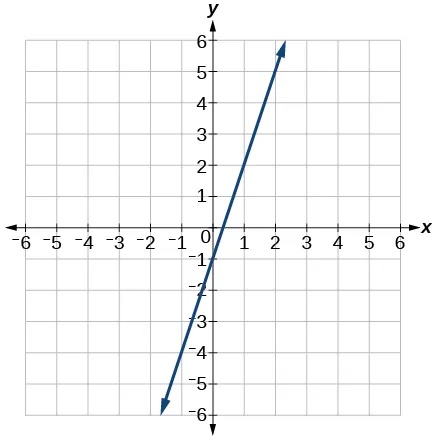
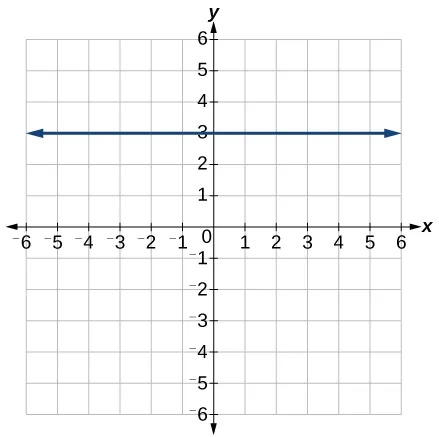
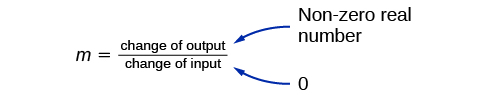
The linear functions we used in the two previous examples increased over time, but not every linear function does. A linear function may be increasing, decreasing, or constant. For an increasing function, as with the train example, the output values increase as the input values increase. The graph of an increasing function has a positive slope. A line with a positive slope slants upward from left to right, as in Figure 5 (a). For a decreasing function, the slope is negative. The output values decrease as the input values increase. A line with a negative slope slants downward from left to right, as in Figure 5 (b). If the function is constant, the output values are the same for all input values so the slope is zero. A line with a slope of zero is horizontal, as in Figure 5 (c).

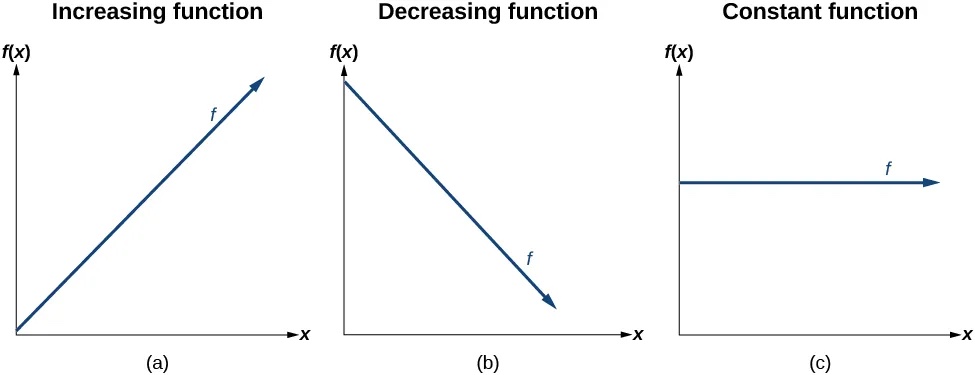
his figure shows three graphs labeled a, b, and c. Graph a shows an increasing function (f) along the x-axis and the y-axis which is labeled f of x. Graph b shows a decreasing function (f) along the x-axis and y-axis which is labeled f of x. Graph c shows a constant function (f) along the x-axis and y-axis which is labeled f of x. The constant function is horizontal. None of the graphs have any increments labeled on the x- or y-axis.
Figure 5

Increasing and Decreasing Functions

The slope determines if the function is an increasing linear function, a decreasing linear function, or a constant function.

  • [latex]f\left(x\right)=mx+b\,[/latex]is an increasing function if[latex]\,m>0.[/latex]
  • [latex]f\left(x\right)=mx+b\,[/latex]is a decreasing function if[latex]\,m\lt0.[/latex]
  • [latex]f\left(x\right)=mx+b\,[/latex]is a constant function if[latex]\,m=0.[/latex]

Deciding Whether a Function Is Increasing, Decreasing, or Constant

Some recent studies suggest that a teenager sends an average of 60 texts per day[2] . For each of the following scenarios, find the linear function that describes the relationship between the input value and the output value. Then, determine whether the graph of the function is increasing, decreasing, or constant.

  1. The total number of texts a teen sends is considered a function of time in days. The input is the number of days, and output is the total number of texts sent.
  2. A teen has a limit of 500 texts per month in his or her data plan. The input is the number of days, and output is the total number of texts remaining for the month.
  3. A teen has an unlimited number of texts in his or her data plan for a cost of $50 per month. The input is the number of days, and output is the total cost of texting each month.
Show Solution

Analyze each function.

  1. The function can be represented as[latex]\,f\left(x\right)=60x\,[/latex], where[latex]\,x\,[/latex]is the number of days. The slope, 60, is positive, so the function is increasing. This makes sense because the total number of texts increases with each day.
  2. The function can be represented as[latex]\,f\left(x\right)=500-60x\,[/latex], where[latex]\,x[/latex]is the number of days. In this case, the slope is negative, so the function is decreasing. This makes sense because the number of texts remaining decreases each day and this function represents the number of texts remaining in the data plan after[latex]\,x\,[/latex]days.
  3. The cost function can be represented as[latex]\,f\left(x\right)=50\,[/latex]because the number of days does not affect the total cost. The slope is 0, so the function is constant.

Interpreting Slope as a Rate of Change

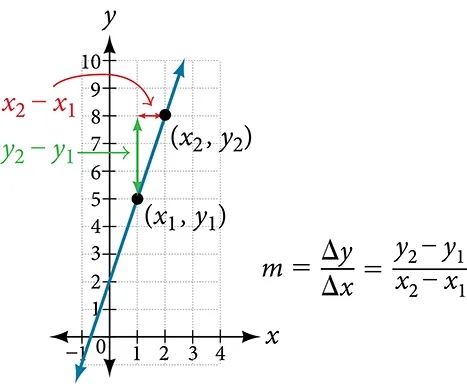
In the examples we have seen so far, the slope was provided to us. However, we often need to calculate the slope given input and output values. Recall that given two values for the input,[latex]\,{x}_{1}[/latex]and[latex]\,{x}_{2},[/latex]and two corresponding values for the output,[latex]\,{y}_{1}\,[/latex]and[latex]\,{y}_{2}\,[/latex]—which can be represented by a set of points,[latex]\,\left({x}_{1}\text{, }{y}_{1}\right)\,[/latex]and[latex]\,\left({x}_{2}\text{, }{y}_{2}\right)[/latex]—we can calculate the slope [latex]m.[/latex]

[latex]m=\frac{\text{change in output (rise)}}{\text{change in input (run)}}=\frac{\Delta y}{\Delta x}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]

Note that in function notation we can obtain two corresponding values for the output[latex]\,{y}_{1}\,[/latex]and[latex]\,{y}_{2}\,[/latex]for the function[latex]\,f,[/latex][latex]\,{y}_{1}=f\left({x}_{1}\right)\,[/latex]and[latex]\,{y}_{2}=f\left({x}_{2}\right),[/latex], so we could equivalently write

[latex]m=\frac{f\left({x}_{2}\right)–f\left({x}_{1}\right)}{{x}_{2}–{x}_{1}}[/latex]

Figure 6 indicates how the slope of the line between the points, [latex]\left({x}_{1},{y}_{1}\right)[/latex]and[latex]\left({x}_{2},{y}_{2}\right),[/latex] is calculated. Recall that the slope measures steepness, or slant. The greater the absolute value of the slope, the steeper the slant is.

This graph shows how to calculate the slope of a line. The line is graphed on an x y coordinate plane. The x-axis is labeled from negative 1 to 6. The y-axis is labeled from negative 1 to 10. The line passes through several points, but two are marked specifcally. The first is labeled (x subscript 1, y subscript 1). It is located at the point (1, 5). The second point is labeled (x subscript 2, y subscript 2). It is located at the point (2, 8). There is a small arrow that runs horizontally from point (2, 8) to point (1, 8). This arrow is labeled x subscript 2 minus x subscript 1. There is a blue arrow that runs vertically from point (1, 5) to point (1, 8) and is labeled y subscript 2 minus y subscript 1. Off to the side is the equation m equals delta y divided by delta x which equals y subscript 2 minus y subscript 1 divided by x subscript 2 minus x subscript 1.
Figure 6. The slope of a function is calculated by the change in [latex]y[/latex]divided by the change in [latex]x.[/latex]It does not matter which coordinate is used as the [latex]({x}_{2,}{y}_{2})[/latex] and which is the [latex]({x}_{1},{y}_{1}),[/latex] as long as each calculation is started with the elements from the same coordinate pair.

Are the units for slope always[latex]\,\frac{\text{units for the output}}{\text{units for the input}}\,\text{?}[/latex]

Yes. Think of the units as the change of output value for each unit of change in input value. An example of slope could be miles per hour or dollars per day. Notice the units appear as a ratio of units for the output per units for the input.

Calculate Slope

The slope, or rate of change, of a function[latex]\,m\,[/latex]can be calculated according to the following:

[latex]m=\frac{\text{change in output (rise)}}{\text{change in input (run)}}=\frac{\Delta y}{\Delta x}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]

where[latex]\,{x}_{1}\,[/latex]and[latex]\,{x}_{2}\,[/latex]are input values,[latex]\,{y}_{1}\,[/latex]and[latex]\,{y}_{2}\,[/latex]are output values.

How To

Given two points from a linear function, calculate and interpret the slope.

  1. Determine the units for output and input values.
  2. Calculate the change of output values and change of input values.
  3. Interpret the slope as the change in output values per unit of the input value.

Finding the Slope of a Linear Function

If[latex]\,f\left(x\right)\,[/latex]is a linear function, and[latex]\,\left(3,-2\right)\,[/latex]and[latex]\,\left(8,1\right)\,[/latex]are points on the line, find the slope. Is this function increasing or decreasing?

Show Solution

The coordinate pairs are[latex]\,\left(3,-2\right)\,[/latex]and[latex]\,\left(8,1\right).\,[/latex]To find the rate of change, we divide the change in output by the change in input.

[latex]m=\frac{\text{change in output}}{\text{change in input}}=\frac{1-\left(-2\right)}{8-3}=\frac{3}{5}[/latex]

We could also write the slope as[latex]\,m=0.6.\,[/latex]The function is increasing because[latex]\,m>0.[/latex]

Analysis

As noted earlier, the order in which we write the points does not matter when we compute the slope of the line as long as the first output value, or y-coordinate, used corresponds with the first input value, or x-coordinate, used. Note that if we had reversed them, we would have obtained the same slope.

[latex]m=\frac{\left(-2\right)-\left(1\right)}{3-8}=\frac{-3}{-5}=\frac{3}{5}[/latex]

 

Try It

If[latex]\,f\left(x\right)\,[/latex]is a linear function, and[latex]\,\left(2,3\right)\,[/latex]and[latex]\,\left(0,4\right)\,[/latex]are points on the line, find the slope. Is this function increasing or decreasing?

Show Solution

[latex]m=\frac{4-3}{0-2}=\frac{1}{-2}=-\frac{1}{2};[/latex] decreasing because [latex]\,m\lt0.[/latex]

Finding the Population Change from a Linear Function

The population of a city increased from 23,400 to 27,800 between 2008 and 2012. Find the change in population per year if we assume the change was constant from 2008 to 2012.

Show Solution

The rate of change relates the change in population to the change in time. The population increased by[latex]\,27,800-23,400=4400\,[/latex]people over the four-year time interval. To find the rate of change, divide the change in the number of people by the number of years.

[latex]\frac{\text{4,400 people}}{\text{4 years}}=\text{1,100 }\frac{\text{people}}{\text{year}}[/latex]

So the population increased by 1,100 people per year.

Analysis

Because we are told that the population increased, we would expect the slope to be positive. This positive slope we calculated is therefore reasonable.

Try It

The population of a small town increased from 1,442 to 1,868 between 2009 and 2012. Find the change in population per year if we assume the change was constant from 2009 to 2012.

Show Solution
[latex]m=\frac{1,868-1,442}{2,012-2,009}=\frac{426}{3}=\text{142 people per year}[/latex]

Writing and Interpreting an Equation for a Linear Function

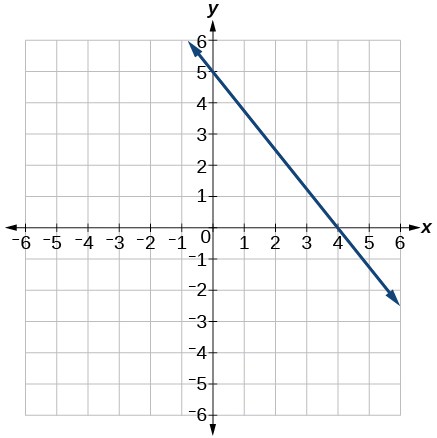
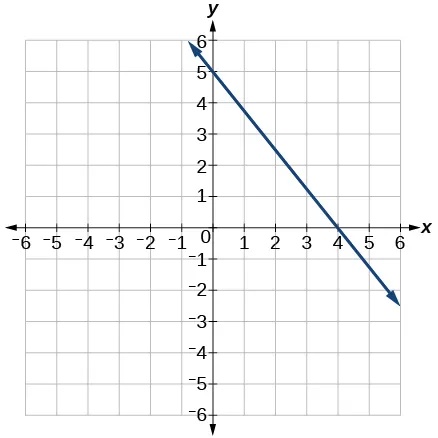
Recall from Equations and Inequalities that we wrote equations in both the slope-intercept form and the point-slope form. Now we can choose which method to use to write equations for linear functions based on the information we are given. That information may be provided in the form of a graph, a point and a slope, two points, and so on. Look at the graph of the function[latex]\,f\,[/latex]in Figure 7.

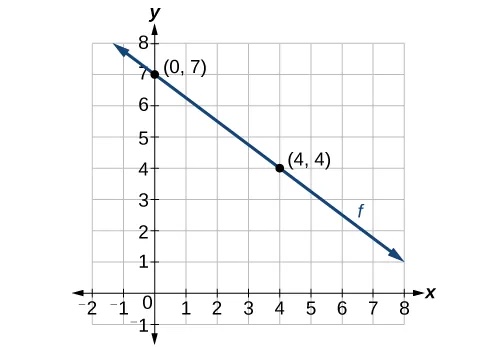
his graph shows a linear function graphed on an x y coordinate plane. The x axis is labeled from negative 2 to 8 and the y axis is labeled from negative 1 to 8. The function f is graph along the points (0, 7) and (4, 4).
Figure 7

We are not given the slope of the line, but we can choose any two points on the line to find the slope. Let’s choose[latex]\,\left(0,7\right)\,[/latex]and[latex]\,\left(4,4\right).\,[/latex]

[latex]\begin{array}{ccc}\hfill m& =& \frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\hfill \\ & =& \frac{4-7}{4-0}\hfill \\ & =& -\frac{3}{4}\hfill \end{array}[/latex]

Now we can substitute the slope and the coordinates of one of the points into the point-slope form.

[latex]\begin{array}{ccc}\hfill y-{y}_{1}& =& m\left(x-{x}_{1}\right)\hfill \\ \hfill \text{ }y-4& =& -\frac{3}{4}\left(x-4\right)\hfill \end{array}[/latex]

If we want to rewrite the equation in the slope-intercept form, we would find

[latex]\begin{array}{ccc}\hfill y-4& =& -\frac{3}{4}\left(x-4\right)\hfill \\ \hfill y-4& =& -\frac{3}{4}x+3\hfill \\ \hfill y& =& -\frac{3}{4}x+7\hfill \end{array}[/latex]

If we want to find the slope-intercept form without first writing the point-slope form, we could have recognized that the line crosses the y-axis when the output value is 7. Therefore,[latex]\,b=7.\,[/latex]We now have the initial value[latex]\,b\,[/latex]and the slope[latex]\,m\,[/latex], so we can substitute[latex]\,m\,[/latex]and[latex]\,b\,[/latex]into the slope-intercept form of a line.

 

This image shows the equation f of x equals m times x plus b. It shows that m is the value negative three fourths and b is 7. It then shows the equation rewritten as f of x equals negative three fourths times x plus 7.

 

So the function is[latex]f\left(x\right)=-\frac{3}{4}x+7,[/latex] and the linear equation would be[latex]\,y=-\frac{3}{4}x+7.[/latex]

How To

Given the graph of a linear function, write an equation to represent the function.

  1. Identify two points on the line.
  2. Use the two points to calculate the slope.
  3. Determine where the line crosses the y-axis to identify the y-intercept by visual inspection.
  4. Substitute the slope and y-intercept into the slope-intercept form of a line equation.

Writing an Equation for a Linear Function

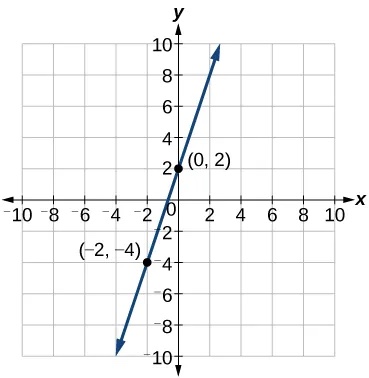
Write an equation for a linear function given a graph of[latex]\,f\,[/latex]shown in Figure 8.

This figure shows an increasing function graphed on an x y coordinate plane. The x axis is labeled from negative 10 to 10. The y axis is labeled from negative 10 to 10. The function passes through the points (0, 2) and (-2, -4). These points are not labeled on this graph.
Figure 8
Show Solution

Identify two points on the line, such as[latex]\,\left(0,2\right)\,[/latex]and[latex]\,\left(-2,-4\right).\,[/latex]Use the points to calculate the slope.

[latex]\begin{array}{ccc}\hfill m& =& \frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\hfill \\ & =& \frac{-4-2}{-2-0}\hfill \\ & =& \frac{-6}{-2}\hfill \\ & =& 3\hfill \end{array}[/latex]

Substitute the slope and the coordinates of one of the points into the point-slope form.

[latex]\begin{array}{ccc}\hfill y-{y}_{1}& =& m\left(x-{x}_{1}\right)\hfill \\ \hfill y-\left(-4\right)& =& 3\left(x-\left(-2\right)\right)\hfill \\ \hfill y+4& =& 3\left(x+2\right)\hfill \end{array}[/latex]

We can use algebra to rewrite the equation in the slope-intercept form.

[latex]\begin{array}{ccc}\hfill y+4& =& 3\left(x+2\right)\hfill \\ \hfill y+4& =& 3x+6\hfill \\ \hfill y& =& 3x+2\hfill \end{array}[/latex]

Analysis

This makes sense because we can see from Figure 9 that the line crosses the y-axis at the point[latex]\,\left(0,\text{ }2\right),\,[/latex]which is the y-intercept, so[latex]\,b=2.[/latex]

This figure shows an increasing function graphed on an x y coordinate plane. The x axis is labeled from negative 10 to 10. The y axis is labeled from negative 10 to 10. The function passes through the points (0, 2) and (-2, -4). These points are labeled on this graph.
Figure 9

Writing an Equation for a Linear Cost Function

Suppose Ben starts a company in which he incurs a fixed cost of $1,250 per month for the overhead, which includes his office rent. His production costs are $37.50 per item. Write a linear function[latex]\,C\,[/latex]where[latex]\,C\left(x\right)\,[/latex]is the cost for[latex]\,x\,[/latex]items produced in a given month.

Show Solution

The fixed cost is present every month, $1,250. The costs that can vary include the cost to produce each item, which is $37.50. The variable cost, called the marginal cost, is represented by[latex]\,37.5.\,[/latex]The cost Ben incurs is the sum of these two costs, represented by[latex]\,C\left(x\right)=1250+37.5x.[/latex]

Analysis

If Ben produces 100 items in a month, his monthly cost is found by substituting 100 for[latex]\,x.[/latex]

[latex]\begin{array}{ccc}\hfill C\left(100\right)& =& 1250+37.5\left(100\right)\hfill \\ & =& 5000\hfill \end{array}[/latex]

So his monthly cost would be $5,000.

Writing an Equation for a Linear Function Given Two Points

If[latex]\,f\,[/latex]is a linear function, with[latex]\,f\left(3\right)=-2,[/latex]and[latex]\,f\left(8\right)=1,[/latex] find an equation for the function in slope-intercept form.

Show Solution

We can write the given points using coordinates.

[latex]\begin{array}{ccc}\hfill f\left(3\right)& =& -2\to \left(3,-2\right)\hfill \\ \hfill f\left(8\right)& =& 1\to \left(8,1\right)\hfill \end{array}[/latex]

We can then use the points to calculate the slope.

[latex]\begin{array}{ccc}\hfill m& =& \frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\hfill \\ & =& \frac{1-\left(-2\right)}{8-3}\hfill \\ & =& \frac{3}{5}\hfill \end{array}[/latex]

Substitute the slope and the coordinates of one of the points into the point-slope form.

[latex]\begin{array}{ccc}\hfill y-{y}_{1}& =& m\left(x-{x}_{1}\right)\hfill \\ \hfill y-\left(-2\right)& =& \frac{3}{5}\left(x-3\right)\hfill \end{array}[/latex]

We can use algebra to rewrite the equation in the slope-intercept form.

[latex]\begin{array}{ccc}\hfill y+2& =& \frac{3}{5}\left(x-3\right)\hfill \\ \hfill y+2& =& \frac{3}{5}x-\frac{9}{5}\hfill \\ \hfill y& =& \frac{3}{5}x-\frac{19}{5}\hfill \end{array}[/latex]

Try It

If[latex]\,f\left(x\right)\,[/latex]is a linear function, with[latex]\,f\left(2\right)=–11,[/latex] and[latex]\,f\left(4\right)=-25,[/latex] write an equation for the function in slope-intercept form.

Show Solution

[latex]y=-7x+3[/latex]

 

Modeling Real-World Problems with Linear Functions

In the real world, problems are not always explicitly stated in terms of a function or represented with a graph. Fortunately, we can analyze the problem by first representing it as a linear function and then interpreting the components of the function. As long as we know, or can figure out, the initial value and the rate of change of a linear function, we can solve many different kinds of real-world problems.

How To

Given a linear function[latex]\,f\,[/latex]and the initial value and rate of change, evaluate[latex]\,f\left(c\right).[/latex]

  1. Determine the initial value and the rate of change (slope).
  2. Substitute the values into[latex]\,f\left(x\right)=mx+b.[/latex]
  3. Evaluate the function at[latex]\,x=c.[/latex]

Using a Linear Function to Determine the Number of Songs in a Music Collection

Marcus currently has 200 songs in his music collection. Every month, he adds 15 new songs. Write a formula for the number of songs,[latex]\,N,[/latex] in his collection as a function of time,[latex]\,t,[/latex] the number of months. How many songs will he own at the end of one year?

Show Solution

The initial value for this function is 200 because he currently owns 200 songs, so[latex]\,N\left(0\right)=200,[/latex]which means that[latex]\,b=200.[/latex]

The number of songs increases by 15 songs per month, so the rate of change is 15 songs per month. Therefore we know that[latex]\,m=15.\,[/latex]We can substitute the initial value and the rate of change into the slope-intercept form of a line.

This image shows the equation f of x equals m times x plus b. It shows that m is the value 15 and b is 200. It then shows the equation rewritten as N of t equals 15 times t plus 200.

We can write the formula[latex]\,N\left(t\right)=15t+200.[/latex]

With this formula, we can then predict how many songs Marcus will have at the end of one year (12 months). In other words, we can evaluate the function at[latex]\,t=12.[/latex]

[latex]\begin{array}{ccc}N\left(12\right)& =& 15\left(12\right)+200\hfill \\ & =& 180+200\hfill \\ & =& 380\hfill \end{array}[/latex]

Marcus will have 380 songs in 12 months.

Analysis

Notice that N is an increasing linear function. As the input (the number of months) increases, the output (number of songs) increases as well.

Using a Linear Function to Calculate Salary Based on Commission

Working as an insurance salesperson, Ilya earns a base salary plus a commission on each new policy. Therefore, Ilya’s weekly income, [latex]\,I,[/latex] depends on the number of new policies,[latex]\,n,[/latex]he sells during the week. Last week he sold 3 new policies and earned $760 for the week. The week before, he sold 5 new policies and earned $920. Find an equation for[latex]\,I\left(n\right),[/latex] and interpret the meaning of the components of the equation.

Show Solution

The given information gives us two input-output pairs:[latex]\,\left(3,760\right)\,[/latex]and[latex]\,\left(5,\text{92}0\right).\,[/latex]We start by finding the rate of change.

[latex]\begin{array}{ccc}\hfill m& =& \frac{920-760}{5-3}\hfill \\ & =& \frac{$160}{2 \text{policies}}\hfill \\ & =& \text{\$}80\,\text{per}\,\text{policy}\hfill \end{array}[/latex]

Keeping track of units can help us interpret this quantity. Income increased by $160 when the number of policies increased by 2, so the rate of change is $80 per policy. Therefore, Ilya earns a commission of $80 for each policy sold during the week.

We can then solve for the initial value.

[latex]\begin{array}{cccc}\hfill I\left(n\right)& =& 80n+b\hfill & \\ \hfill 760& =& 80\left(3\right)+b\hfill & \phantom{\rule{1em}{0ex}}\text{ }\text{when}\,n=3,I\left(3\right)=760\hfill \\ \hfill 760& -& 80\left(3\right)=b\hfill & \\ \hfill 520& =& b\hfill & \end{array}[/latex]

The value of[latex]\,b\,[/latex]is the starting value for the function and represents Ilya’s income when[latex]\,n=0,\,[/latex]or when no new policies are sold. We can interpret this as Ilya’s base salary for the week, which does not depend on the number of policies sold.

We can now write the final equation.

[latex]I\left(n\right)=80n+520[/latex]

Our final interpretation is that Ilya’s base salary is $520 per week and he earns an additional $80 commission for each policy sold.

Using Tabular Form to Write an Equation for a Linear Function

Table 1 relates the number of rats in a population to time, in weeks. Use the table to write a linear equation.

number of weeks, w 0 2 4 6
number of rats, P(w) 1000 1080 1160 1240

Table 1

Show Solution

We can see from the table that the initial value for the number of rats is 1000, so[latex]\,b=1000.[/latex]

Rather than solving for[latex]\,m,[/latex] we can tell from looking at the table that the population increases by 80 for every 2 weeks that pass. This means that the rate of change is 80 rats per 2 weeks, which can be simplified to 40 rats per week.

[latex]P\left(w\right)=40w+1000[/latex]

If we did not notice the rate of change from the table, we could still solve for the slope using any two points from the table. For example, using[latex]\,\left(2,1080\right)\,[/latex]and[latex]\,\left(6,1240\right)[/latex]

[latex]\begin{array}{ccc}\hfill m& =& \frac{1240-1080}{6-2}\hfill \\ & =& \frac{160}{4}\hfill \\ & =& 40\hfill \end{array}[/latex]

Is the initial value always provided in a table of values like Table 1?

No. Sometimes the initial value is provided in a table of values, but sometimes it is not. If you see an input of 0, then the initial value would be the corresponding output. If the initial value is not provided because there is no value of input on the table equal to 0, find the slope, substitute one coordinate pair and the slope into[latex]\,f\left(x\right)=mx+b,\,[/latex]and solve for[latex]\,b.[/latex]

Try It

A new plant food was introduced to a young tree to test its effect on the height of the tree. Table 2 shows the height of the tree, in feet,[latex]\,x\,[/latex]months since the measurements began. Write a linear function,[latex]\,H\left(x\right),[/latex] where[latex]\,x\,[/latex]is the number of months since the start of the experiment.

x 0 2 4 8 12
H(x) 12.5 13.5 14.5 16.5 18.5

Table 2

Show Solution

[latex]H\left(x\right)=0.5x+12.5[/latex]

Graphing Linear Functions

Now that we’ve seen and interpreted graphs of linear functions, let’s take a look at how to create the graphs. There are three basic methods of graphing linear functions. The first is by plotting points and then drawing a line through the points. The second is by using the y-intercept and slope. And the third method is by using transformations of the identity function[latex]\,f\left(x\right)=x.[/latex]

Graphing a Function by Plotting Points

To find points of a function, we can choose input values, evaluate the function at these input values, and calculate output values. The input values and corresponding output values form coordinate pairs. We then plot the coordinate pairs on a grid. In general, we should evaluate the function at a minimum of two inputs in order to find at least two points on the graph. For example, given the function[latex]\,f\left(x\right)=2x,[/latex] we might use the input values 1 and 2. Evaluating the function for an input value of 1 yields an output value of 2, which is represented by the point[latex]\,\left(1,2\right).\,[/latex]Evaluating the function for an input value of 2 yields an output value of 4, which is represented by the point[latex]\,\left(2,4\right).\,[/latex]Choosing three points is often advisable because if all three points do not fall on the same line, we know we made an error.

How To

Given a linear function, graph by plotting points.

  1. Choose a minimum of two input values.
  2. Evaluate the function at each input value.
  3. Use the resulting output values to identify coordinate pairs.
  4. Plot the coordinate pairs on a grid.
  5. Draw a line through the points.

Graphing by Plotting Points

Graph[latex]\,f\left(x\right)=-\frac{2}{3}x+5\,[/latex]by plotting points.

Show Solution

Begin by choosing input values. This function includes a fraction with a denominator of 3, so let’s choose multiples of 3 as input values. We will choose 0, 3, and 6.

Evaluate the function at each input value, and use the output value to identify coordinate pairs.

[latex]\begin{array}{cc}\hfill x=0& \phantom{\rule{2em}{0ex}}f\left(0\right)=-\frac{2}{3}\left(0\right)+5=5⇒\left(0,5\right)\hfill \\ \hfill x=3& \phantom{\rule{2em}{0ex}}f\left(3\right)=-\frac{2}{3}\left(3\right)+5=3⇒\left(3,3\right)\hfill \\ \hfill x=6& \phantom{\rule{2em}{0ex}}f\left(6\right)=-\frac{2}{3}\left(6\right)+5=1⇒\left(6,1\right)\hfill \end{array}[/latex]

Plot the coordinate pairs and draw a line through the points. Figure 10 represents the graph of the function[latex]\,f\left(x\right)=-\frac{2}{3}x+5.[/latex]

This graph shows a decreasing function graphed on an x y coordinate plane. The x axis runs from negative 4 to 7 and the y axis runs from negative 2 to 7. The y axis is labeled f of x. The function passes through the points (0, 5), (3, 3) and (6, 1)
Figure 10 The graph of the linear function[latex]f\left(x\right)=-\frac{2}{3}x+5.[/latex]

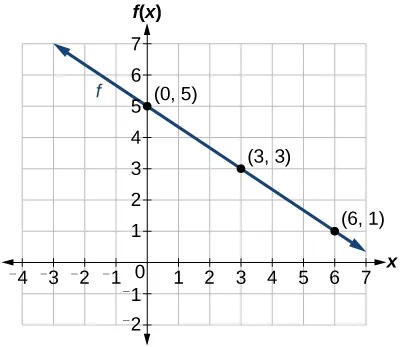
Analysis

The graph of the function is a line, as expected for a linear function. In addition, the graph has a downward slant, which indicates a negative slope. This is also expected from the negative, constant rate of change in the equation for the function.

Try It

Graph[latex]\,f\left(x\right)=-\frac{3}{4}x+6\,[/latex]by plotting points.

Show Solution

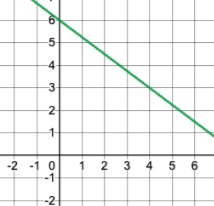
Graph of the line y equals negative three fourths plus 6. The function passes through the points (0,6), (4,3) and (8,0).

Graphing a Function Using y-intercept and Slope

Another way to graph linear functions is by using specific characteristics of the function rather than plotting points. The first characteristic is its y-intercept, which is the point at which the input value is zero. To find the y-intercept, we can set[latex]\,x=0\,[/latex]in the equation.

The other characteristic of the linear function is its slope.

Let’s consider the following function.

[latex]f\left(x\right)=\frac{1}{2}x+1[/latex]

The slope is[latex]\,\frac{1}{2}.\,[/latex]Because the slope is positive, we know the graph will slant upward from left to right. The y-intercept is the point on the graph when[latex]\,x=0.\,[/latex]The graph crosses the y-axis at[latex]\,\left(0,1\right).\,[/latex]Now we know the slope and the y-intercept. We can begin graphing by plotting the point[latex]\,\left(0,1\right).\,[/latex]We know that the slope is the change in the y-coordinate over the change in the x-coordinate. This is commonly referred to as rise over run,[latex]\,m=\frac{\text{rise}}{\text{run}}.\,[/latex]From our example, we have[latex]\,m=\frac{1}{2},[/latex]which means that the rise is 1 and the run is 2. So starting from our y-intercept[latex]\,\left(0,1\right),[/latex] we can rise 1 and then run 2, or run 2 and then rise 1. We repeat until we have a few points, and then we draw a line through the points, as shown in Figure 11.

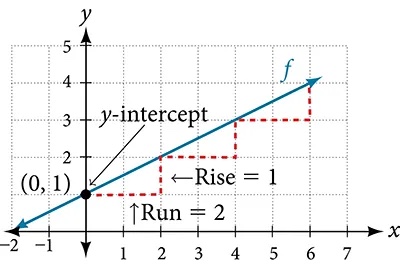
This graph shows how to calculate the rise over run for the slope on an x, y coordinate plane. The x-axis runs from negative 2 to 7. The y-axis runs from negative 2 to 5. The line extends right and upward from point (0,1), which is the y-intercept. A dotted line extends two units to the right from point (0, 1) and is labeled Run = 2. The same dotted line extends upwards one unit and is labeled Rise =1.
Figure 11

Graphical Interpretation of a Linear Function

In the equation[latex]\,f\left(x\right)=mx+b[/latex]

  • [latex]b\,[/latex]is the y-intercept of the graph and indicates the point[latex]\,\left(0,b\right)\,[/latex]at which the graph crosses the y-axis.
  • [latex]m\,[/latex]is the slope of the line and indicates the vertical displacement (rise) and horizontal displacement (run) between each successive pair of points. Recall the formula for the slope:
[latex]m=\frac{\text{change in output (rise)}}{\text{change in input (run)}}=\frac{\Delta y}{\Delta x}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]

Do all linear functions have y-intercepts?

Yes. All linear functions cross the y-axis and therefore have y-intercepts. (Note: A vertical line that is parallel to the y-axis does not have a y-intercept, but it is not a function.)

How To

Given the equation for a linear function, graph the function using the y-intercept and slope.

  1. Evaluate the function at an input value of zero to find the y-intercept.
  2. Identify the slope as the rate of change of the input value.
  3. Plot the point represented by the y-intercept.
  4. Use[latex]\,\frac{\text{rise}}{\text{run}}\,[/latex]to determine at least two more points on the line.
  5. Sketch the line that passes through the points.

Graphing by Using the y-intercept and Slope

Graph[latex]\,f\left(x\right)=-\frac{2}{3}x+5\,[/latex]using the y-intercept and slope.

Show Solution

Evaluate the function at[latex]\,x=0\,[/latex]to find the y-intercept. The output value when[latex]\,x=0\,[/latex]is 5, so the graph will cross the y-axis at[latex]\,\left(0,5\right).[/latex]

According to the equation for the function, the slope of the line is[latex]\,-\frac{2}{3}.\,[/latex]This tells us that for each vertical decrease in the “rise” of[latex]\,–2\,[/latex]units, the “run” increases by 3 units in the horizontal direction. We can now graph the function by first plotting the y-intercept on the graph in Figure 12. From the initial value[latex]\,\left(0,5\right)\,[/latex]we move down 2 units and to the right 3 units. We can extend the line to the left and right by repeating and then drawing a line through the points.

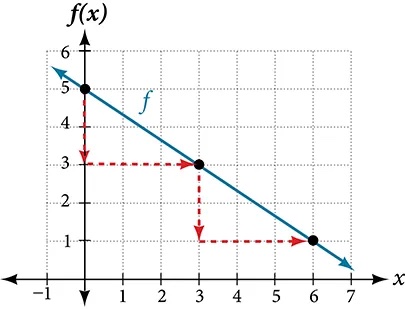
This graph shows a decreasing function graphed on an x y coordinate plane. The x-axis runs from negative 3 to 7, and the y-axis runs from negative 1 to 7. The function passes through the points (0,5); (3,3); and (6,1). Arrows extend downward two units and to the right three units from each point to the next point.
Figure 12 Graph of [latex]f\left(x\right)=-\frac{2}{3}x+5[/latex] and shows how to calculate the rise over run for the slope.

Analysis

The graph slants downward from left to right, which means it has a negative slope as expected.

Try It

Find a point on the graph we drew in Figure 12 that has a negative x-value.

Show Solution

Possible answers include[latex]\left(-3,7\right),\,[/latex]
[latex]\left(-6,9\right),\,[/latex]or[latex]\,\left(-9,11\right).[/latex]

 

Graphing a Function Using Transformations

Another option for graphing is to use a transformation of the identity function[latex]\,f\left(x\right)=x.\,[/latex]A function may be transformed by a shift up, down, left, or right. A function may also be transformed using a reflection, stretch, or compression.

Vertical Stretch or Compression

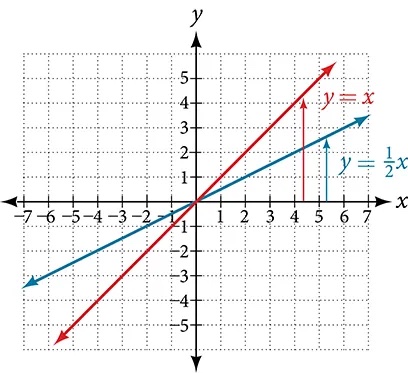
In the equation[latex]\,f\left(x\right)=mx,[/latex] the[latex]\,m\,[/latex]is acting as the vertical stretch or compression of the identity function. When[latex]\,m\,[/latex]is negative, there is also a vertical reflection of the graph. Notice in Figure 14 that multiplying the equation of[latex]\,f\left(x\right)=x\,[/latex]by[latex]\,m\,[/latex]stretches the graph of[latex]\,f\,[/latex]by a factor of[latex]\,m\,[/latex]units if[latex]\,m>\text{1}\,[/latex]and compresses the graph of[latex]\,f\,[/latex]by a factor of[latex]\,m\,[/latex]units if[latex]\,01.\,[/latex]This means the larger the absolute value of[latex]\,m,\,[/latex]the steeper the slope.

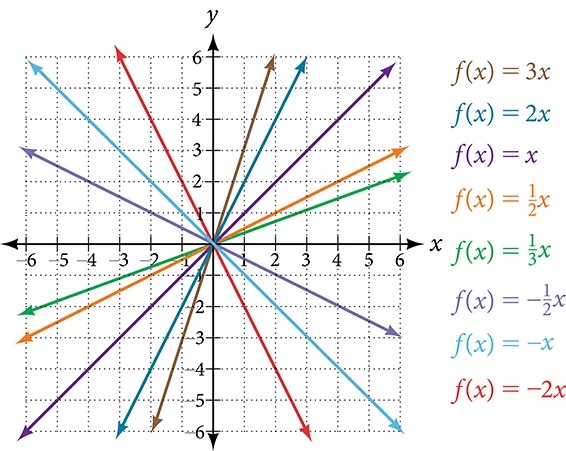
This graph shows seven versions of the function, f of x = x on an x, y coordinate plane. The x-axis runs from negative 8 to 8. The y-axis runs from negative 8 to 8. Seven multi-colored lines run through the point (0, 0). Starting with the lines in the top right quadrant and moving clockwise, the first line is f of x = 3 times x and has a slope of 3, the next line is f of x = 2 times x which has a slope of 2, the next line is f of x = x which has a slope of 1, the next line is f of x = x divided by 2 which has a slope of .5. The last line in this quadrant is f of x = x divided by 3 which has a slope of one third x. In the bottom right quadrant moving clockwise, the first line is f of x = negative x divided by 2, which has a slope of negative one half, the middle line is f of x = negative x which has a slope of negative 1, and the last line is f of x = negative 2 times x which has a slope of negative 2.
Figure 13 Vertical stretches and compressions and reflections on the function [latex] f(x)=x [/latex]

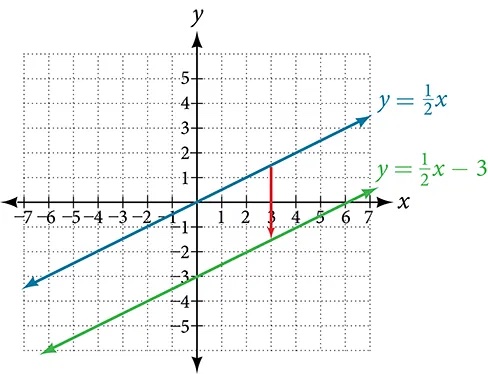
Vertical Shift

In[latex]\,f\left(x\right)=mx+b,[/latex] the[latex]\,b\,[/latex]acts as the vertical shift, moving the graph up and down without affecting the slope of the line. Notice in Figure 14 that adding a value of [latex]b[/latex] to the equation of[latex]f\left(x\right)=x[/latex] shifts the graph of[latex]f[/latex] a total of [latex]b[/latex] units up if [latex]b[/latex] is positive and [latex]|b|[/latex] units down if [latex]b[/latex] is negative.

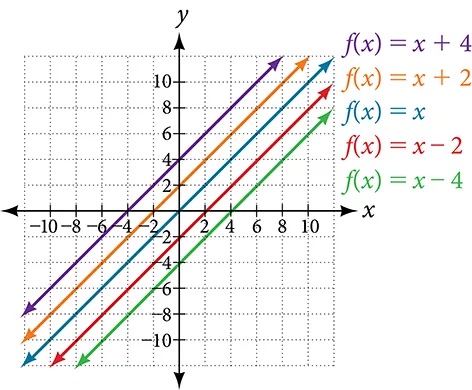
This graph shows five versions of the function, f of x = x, on an x, y coordinate plane. The x-axis runs from negative 8 to 8, and the y axis runs negative 8 to 8. There are five lines parallel to each other. The first line extends from the bottom left quadrant to the upper right quadrant on the coordinate plane. This line shows f of x = x plus 4 which has a slope of 1 and a y-intercept at 4. The next line also extends from the bottom left quadrant to the upper right quadrant and shows f of x = x plus 2 which has a slope of 1 and a y-intercept at 2. The next and middle line, extends from the lower left quadrant, through the center of the graph at point (0, 0) to the upper right quadrant and shows f of x = x. The next line extends from the lower left quadrant, through the lower right quadrant to the upper right quadrant. This line shows f of x = x minus 2 which has a slope of 1 and a y-intercept at -2. The last line extends from the lower left quadrant, through the lower right quadrant to the upper right quadrant.This line shows f of x = x minus 4 which has a slope of 1 and a y-intercept at -4.
Figure 14 This graph illustrates vertical shifts of the function [latex]f\left(x\right)=x.[/latex]

Using vertical stretches or compressions along with vertical shifts is another way to look at identifying different types of linear functions. Although this may not be the easiest way to graph this type of function, it is still important to practice each method.

How To

Given the equation of a linear function, use transformations to graph the linear function in the form[latex]\,f\left(x\right)=mx+b.[/latex]

  1. Graph[latex]\,f\left(x\right)=x.[/latex]
  2. Vertically stretch or compress the graph by a factor[latex]\,m.[/latex]
  3. Shift the graph up or down[latex]\,b\,[/latex]units.

Graphing by Using Transformations

Graph[latex]\,f\left(x\right)=\frac{1}{2}x-3\,[/latex]using transformations.

Show Solution

The equation for the function shows that[latex]\,m=\frac{1}{2}\,[/latex]so the identity function is vertically compressed by[latex]\,\frac{1}{2}.\,[/latex]The equation for the function also shows that[latex]\,b=-3\,[/latex]so the identity function is vertically shifted down 3 units. First, graph the identity function, and show the vertical compression as in Figure 15.

his graph shows two functions on an x, y coordinate plane. One shows an increasing function of y = x divided by 2 that runs through the points (0, 0) and (2, 1). The second shows an increasing function of y = x and runs through the points (0, 0) and (1, 1)).
Figure 15 The function, [latex]y=x[/latex], compressed by a factor of [latex]\frac{1}{2}[/latex] .

Then show the vertical shift as in Figure 16.

This graph shows two functions on an x, y coordinate plane. The first is an increasing function of y = x divided by 2 and runs through the points (0, 0) and (2, 1). The second shows an increasing function of y = x divided by 2 minus 3 and passes through the points (0, 3) and (2, -2). An arrow pointing downward from the first function to the second function reveals the vertical shift.
Figure 16 The function [latex]y=\frac{1}{2}x[/latex] shifted down 3 units.

Try It

Graph[latex]\,f\left(x\right)=4+2x\,[/latex]using transformations.

Show Solution

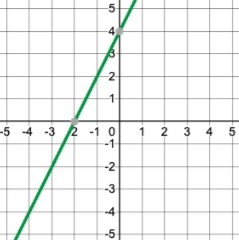
Graph of the line y=2x+4 on an 8 by 8 rectangular grid

In the Graphing by Transformation example [latex]\,f\left(x\right)=\frac{1}{2}x-3\,[/latex], could we have sketched the graph by reversing the order of the transformations?

No. The order of the transformations follows the order of operations. When the function is evaluated at a given input, the corresponding output is calculated by following the order of operations. This is why we performed the compression first. For example, following the order: Let the input be 2.

[latex]\begin{array}{ccc}\hfill f\left(2\right)& =& \frac{1}{2}\left(2\right)-3\hfill \\ & =& 1-3\hfill \\ & =& -2\hfill \end{array}[/latex]

Writing the Equation for a Function from the Graph of a Line

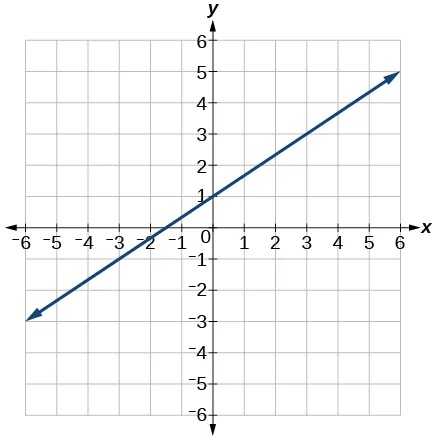
Earlier, we wrote the equation for a linear function from a graph. Now we can extend what we know about graphing linear functions to analyze graphs a little more closely. Begin by taking a look at Figure 17. We can see right away that the graph crosses the y-axis at the point[latex]\,\left(0,\text{4}\right)\,[/latex], so this is the y-intercept.

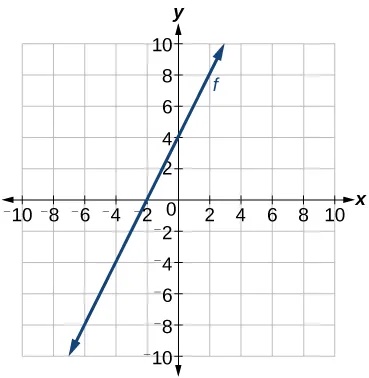
his graph shows the function f of x = 2 times x plus 4 on an x, y coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. This function passes through the points (-2, 0) and (0, 4).
Figure 17

Then we can calculate the slope by finding the rise and run. We can choose any two points, but let’s look at the point[latex]\,\left(–2,0\right).\,[/latex]To get from this point to the y-intercept, we must move up 4 units (rise) and to the right 2 units (run). So the slope must be

[latex]m=\frac{\text{rise}}{\text{run}}=\frac{4}{2}=2[/latex]

Substituting the slope and y-intercept into the slope-intercept form of a line gives

[latex]y=2x+4[/latex]

How To

Given a graph of linear function, find the equation to describe the function.

  1. Identify the y-intercept of an equation.
  2. Choose two points to determine the slope.
  3. Substitute the y-intercept and slope into the slope-intercept form of a line.

Matching Linear Functions to Their Graphs

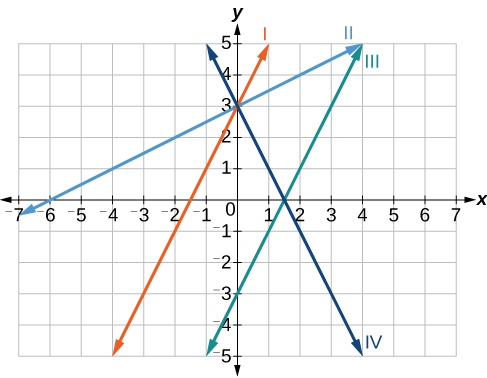
Match each equation of the linear functions with one of the lines in Figure 18.

[latex]\begin{array}{cccc}a\text{.}\hfill & \hfill \text{ }f\left(x\right)& =& 2x+3\hfill \\ b\text{.}\hfill & \hfill g\left(x\right)& =& 2x-3\hfill \\ c\text{.}\hfill & \hfill h\left(x\right)& =& -2x+3\hfill \\ d\text{. }\hfill & \hfill j\left(x\right)& =& \frac{1}{2}x+3\hfill \end{array}[/latex]
Graph of four functions where the orange line has a y-intercept at 3 and slope of 2, the baby blue line has a y-intercept at 3 and slope of 1/2, the blue line has a y-intercept at 3 and slope of -2, and the green line has a y-intercept at -3 and slope of 2.
Figure 18
Show Solution

Analyze the information for each function.

  1. This function has a slope of 2 and a y-intercept of 3. It must pass through the point (0, 3) and slant upward from left to right. We can use two points to find the slope, or we can compare it with the other functions listed. Function[latex]\,g\,[/latex]has the same slope, but a different y-intercept. Lines I and III have the same slant because they have the same slope. Line III does not pass through[latex]\,\left(0,\text{3}\right)\,[/latex]so[latex]\,f\,[/latex]must be represented by line I.
  2. This function also has a slope of 2, but a y-intercept of[latex]\,-3.\,[/latex]It must pass through the point[latex]\,\left(0,-3\right)\,[/latex]and slant upward from left to right. It must be represented by line III.
  3. This function has a slope of –2 and a y-intercept of 3. This is the only function listed with a negative slope, so it must be represented by line IV because it slants downward from left to right.
  4. This function has a slope of[latex]\,\frac{1}{2}\,[/latex]and a y-intercept of 3. It must pass through the point (0, 3) and slant upward from left to right. Lines I and II pass through[latex]\,\left(0,\text{3}\right),[/latex] but the slope of[latex]\,j\,[/latex]is less than the slope of[latex]\,f\,[/latex]so the line for[latex]\,j\,[/latex]must be flatter. This function is represented by Line II.

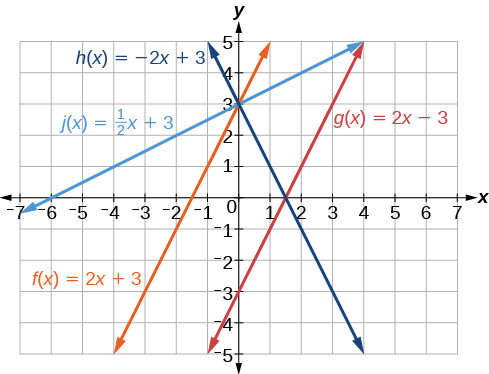
Now we can re-label the lines, as in Figure 19.

Graph of four functions where the blue line is h(x) = -2x + 3 which goes through the point (0,3), the baby blue line is j(x) = x/2 + 3 which goes through the point (0,3). The orange line is f(x) = 2x + 3 which goes through the point (0,3), and the red line is g(x) = 2x – 3 which goes through the point (0,-3)
Figure 19

Finding the x-intercept of a Line

So far we have been finding the y-intercepts of a function: the point at which the graph of the function crosses the y-axis. Recall that a function may also have an x-intercept, which is the x-coordinate of the point where the graph of the function crosses the x-axis. In other words, it is the input value when the output value is zero.

To find the x-intercept, set a function[latex]\,f\left(x\right)\,[/latex]equal to zero and solve for the value of[latex]\,x.\,[/latex]For example, consider the function shown.

[latex]f\left(x\right)=3x-6[/latex]

Set the function equal to 0 and solve for[latex]\,x.[/latex]

[latex]\begin{array}{ccc}\hfill 0& =& 3x-6\hfill \\ \hfill 6& =& 3x\hfill \\ \hfill 2& =& x\hfill \\ \hfill x& =& 2\hfill \end{array}[/latex]

The graph of the function crosses the x-axis at the point[latex]\,\left(2,\text{0}\right).[/latex]

Do all linear functions have x-intercepts?

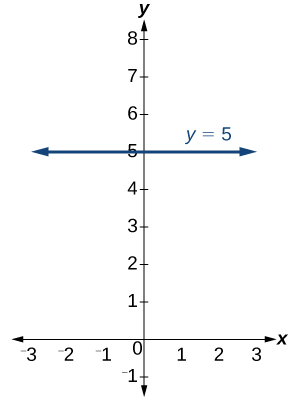
No. However, linear functions of the form[latex]\,y=c,[/latex] where[latex]\,c\,[/latex]is a nonzero real number are the only examples of linear functions with no x-intercept. For example,[latex]\,y=5\,[/latex]is a horizontal line 5 units above the x-axis. This function has no x-intercepts, as shown in Figure 20.

Graph of the function y = 5, a completely horizontal line that goes through the point (0,5). Graphed on an xy-plane with the x-axis ranging from -3 to 3 and the y-plane ranging from -1 to 8.
Figure 20

x-intercept

The x-intercept of the function is value of[latex]\,x\,[/latex]when[latex]\,f\left(x\right)=0.\,[/latex]It can be solved by the equation[latex]\,0=mx+b.[/latex]

Finding an x-intercept

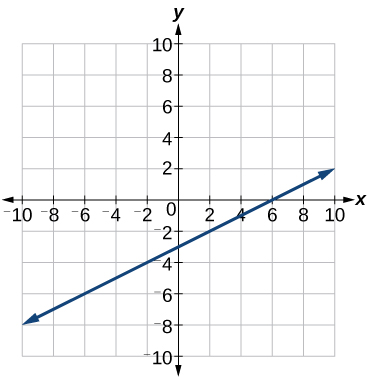
Find the x-intercept of[latex]\,f\left(x\right)=\frac{1}{2}x-3.[/latex]

Show Solution

Set the function equal to zero to solve for[latex]\,x.[/latex]

[latex]\begin{array}{ccc}\hfill 0& =& \frac{1}{2}x-3\hfill \\ \hfill 3& =& \frac{1}{2}x\hfill \\ \hfill 6& =& x\hfill \\ \hfill x& =& 6\hfill \end{array}[/latex]

The graph crosses the x-axis at the point[latex]\,\left(6,\text{0}\right).[/latex]

Analysis

A graph of the function is shown in Figure 21. We can see that the x-intercept is[latex]\,\left(6,\text{0}\right)\,[/latex]as we expected.

Graph of the linear function with the points (6,0) and (0,-3) labeled with a slope of ½.
Figure 21

Try It

Find the x-intercept of[latex]\,f\left(x\right)=\frac{1}{4}x-4.[/latex]

Show Solution

[latex]\,\left(16,\text{ 0}\right)[/latex]

Describing Horizontal and Vertical Lines

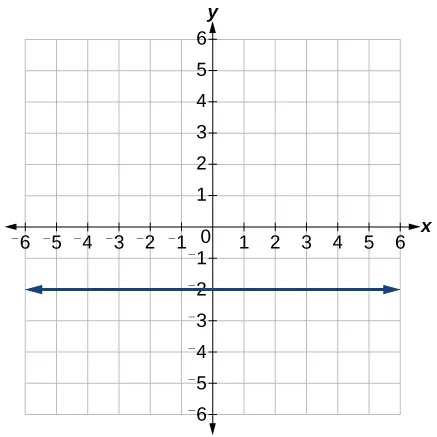
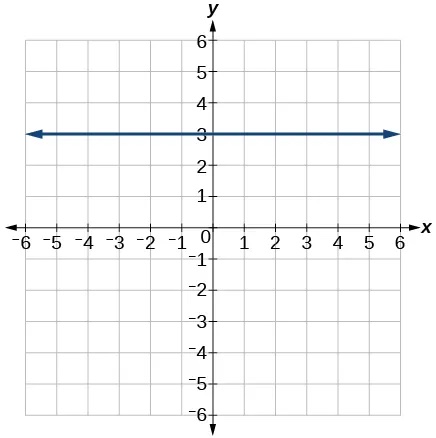
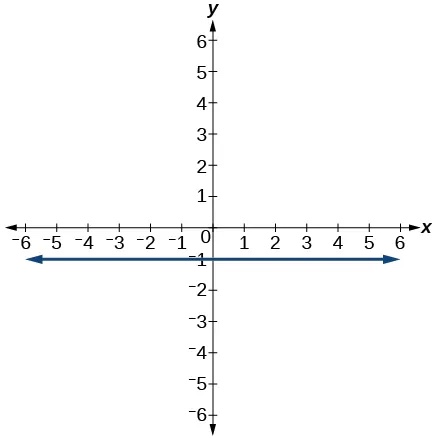
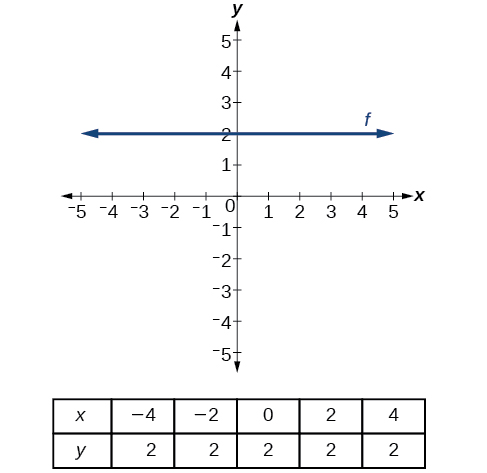
There are two special cases of lines on a graph—horizontal and vertical lines. A horizontal line indicates a constant output, or y-value. In Figure 22, we see that the output has a value of 2 for every input value. The change in outputs between any two points, therefore, is 0. In the slope formula, the numerator is 0, so the slope is 0. If we use[latex]\,m=0\,[/latex]in the equation[latex]\,f\left(x\right)=mx+b,[/latex] the equation simplifies to[latex]\,f\left(x\right)=b.\,[/latex]In other words, the value of the function is a constant. This graph represents the function[latex]\,f\left(x\right)=2.[/latex]

This graph shows the line y = 2 on an x.y coordinate plane. The x-axis runs from negative 5 to 5 and the y-axis runs from – 5 to 5. A horizontal line crosses through the point (0, 2). Underneath the graph is a table with two rows and six columns. The top row is labeled: “x” and has the values negative 4, negative 2, 0, 2, and 4. The bottom row is labeled “y” and has the values 2, 2, 2, 2, and 2.
Figure 22 A horizontal line representing the function 𝑓(𝑥)=2

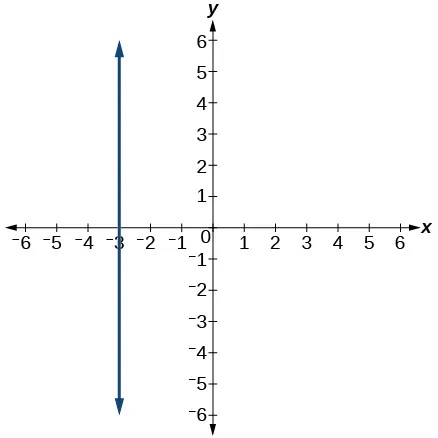
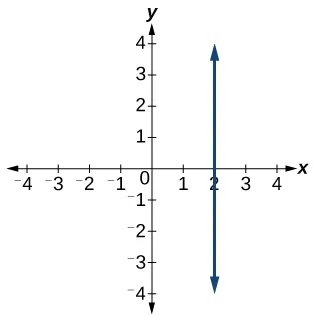
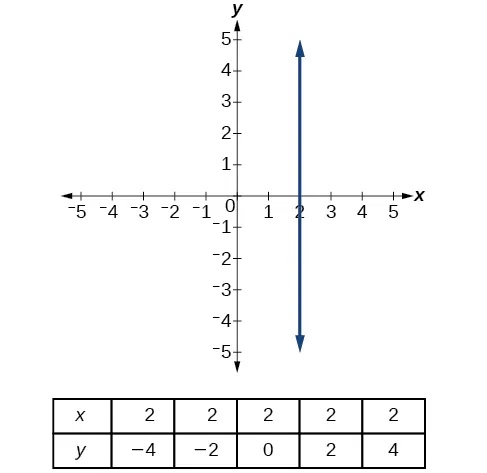
A vertical line indicates a constant input, or x-value. We can see that the input value for every point on the line is 2, but the output value varies. Because this input value is mapped to more than one output value, a vertical line does not represent a function. Notice that between any two points, the change in the input values is zero. In the slope formula, the denominator will be zero, so the slope of a vertical line is undefined.

This is an image showing when a slope is undefined. m = change of output divided by the change of input. The change of output is labeled as: non-zero real number and the change of input is labeled 0.
Figure 23 Example of how a line has a vertical slope. 0 in the denominator of the slope.

 

A vertical line, such as the one in Figure 24, has an x-intercept, but no y-intercept unless it’s the line[latex]\,x=0.\,[/latex]This graph represents the line[latex]\,x=2.[/latex]

"This graph shows a vertical line passing through the point (2, 0) on an x, y coordinate plane. The x-axis runs from negative 5 to 5 and the y-axis runs from negative 5 to 5. Underneath the graph is a table with two rows and six columns. The top row is labeled: “x” and has the values 2, 2, 2, 2, and 2. The bottom row is labeled: “y” and has the values negative 4, negative 2, 0, 2, and 4.
Figure 24The vertical line, 𝑥=2, which does not represent a function

Horizontal and Vertical Lines

Lines can be horizontal or vertical.

A horizontal line is a line defined by an equation in the form[latex]\,f\left(x\right)=b.[/latex]

A vertical line is a line defined by an equation in the form[latex]\,x=a.[/latex]

Writing the Equation of a Horizontal Line

Write the equation of the line graphed in Figure 25.

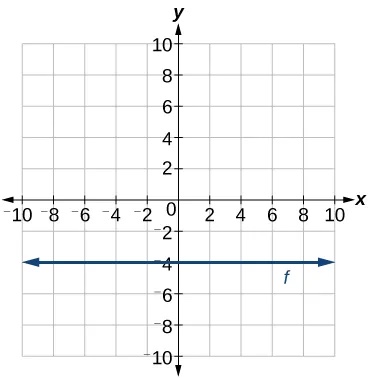
This graph shows the function y = negative 4 on an x, y coordinate plane. The x-axis runs from negative 10 to 10. The y-axis runs from negative 10 to 10. The horizontal line passes through the point, (0, -4).
Figure 25
Show Solution

For any x-value, the y-value is[latex]\,-4,\,[/latex]so the equation is[latex]\,y=-4.[/latex]

Writing the Equation of a Vertical Line

Write the equation of the line graphed in Figure 26.

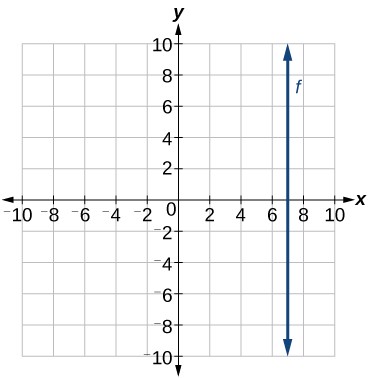
This is a graph showing a line with an undefined slope on an x, y coordinate plane. The x-axis runs from negative 10 to 10 and the y-axis runs from -10 to 10. The line passes through the point (7, 0).
Figure 26
Show Solution

The constant x-value is[latex]\,7,[/latex] so the equation is[latex]\,x=7.[/latex]

 

Key Concepts

  • Linear functions can be represented in words, function notation, tabular form, and graphical form.
  • An increasing linear function results in a graph that slants upward from left to right and has a positive slope. A decreasing linear function results in a graph that slants downward from left to right and has a negative slope. A constant linear function results in a graph that is a horizontal line.
  • Slope is a rate of change. The slope of a linear function can be calculated by dividing the difference between y-values by the difference in corresponding x-values of any two points on the line.
  • An equation for a linear function can be written from a graph.
  • The equation for a linear function can be written if the slope[latex]\,m\,[/latex]and initial value[latex]\,b\,[/latex]are known.
  • A linear function can be used to solve real-world problems given information in different forms.
  • Linear functions can be graphed by plotting points or by using the y-intercept and slope.
  • Graphs of linear functions may be transformed by using shifts up, down, left, or right, as well as through stretches, compressions, and reflections.
  • The equation for a linear function can be written by interpreting the graph.
  • The x-intercept is the point at which the graph of a linear function crosses the x-axis.
  • Horizontal lines are written in the form [latex]\,f\left(x\right)=b.\,[/latex]
  • Vertical lines are written in the form [latex]\,x=b.\,[/latex]
  • Parallel lines have the same slope. Perpendicular lines have negative reciprocal slopes, assuming neither is vertical.
  • A line parallel to another line, passing through a given point, may be found by substituting the slope value of the line and the x– and y-values of the given point into the equation,[latex]\,f\left(x\right)=mx+b,\,[/latex]and using the[latex]\,b\,[/latex]that results. Similarly, the point-slope form of an equation can also be used.
  • A line perpendicular to another line, passing through a given point, may be found in the same manner, with the exception of using the negative reciprocal slope.

Section Exercises

Verbal

  1. Terry is skiing down a steep hill. Terry’s elevation,[latex]\,E\left(t\right),[/latex] in feet after[latex]\,t\,[/latex]seconds is given by[latex]\,E\left(t\right)=3000-70t.\,[/latex]Write a complete sentence describing Terry’s starting elevation and how it is changing over time.
Show Solution

Terry starts at an elevation of 3000 feet and descends 70 feet per second.

  1. Jessica is walking home from a friend’s house. After 2 minutes she is 1.4 miles from home. Twelve minutes after leaving, she is 0.9 miles from home. What is her rate in miles per hour?
  1. A boat is 100 miles away from the marina, sailing directly toward it at 10 miles per hour. Write an equation for the distance of the boat from the marina after t hours.
Show Solution

[latex]d\left(t\right)=100-10t[/latex]

  1. If the graphs of two linear functions are perpendicular, describe the relationship between the slopes and the y-intercepts.
  1. If a horizontal line has the equation[latex]\,f\left(x\right)=a\,[/latex]and a vertical line has the equation[latex]\,x=a,\,[/latex]what is the point of intersection? Explain why what you found is the point of intersection.
Show Solution

The point of intersection is[latex]\,\left(a,\text{ }a\right).\,[/latex]This is because for the horizontal line, all of the[latex]\,y\,[/latex]coordinates are[latex]\,a\,[/latex]and for the vertical line, all of the[latex]\,x\,[/latex]coordinates are[latex]\,a.\,[/latex]The point of intersection is on both lines and therefore will have these two characteristics.

Algebraic

For the following exercises, determine whether the equation of the curve can be written as a linear function.

  1. [latex]y=\frac{1}{4}x+6[/latex]
  1. [latex]y=3x-5[/latex]
Show Solution

Yes

  1. [latex]y=3{x}^{2}-2[/latex]
  1. [latex]3x+5y=15[/latex]
Show Solution

Yes

  1. [latex]3{x}^{2}+5y=15[/latex]
  1. [latex]3x+5{y}^{2}=15[/latex]
Show Solution

No

  1. [latex]-2{x}^{2}+3{y}^{2}=6[/latex]
  1. [latex]-\frac{x-3}{5}=2y[/latex]
Show Solution

Yes

For the following exercises, determine whether each function is increasing or decreasing.

  1. [latex]f\left(x\right)=4x+3[/latex]
  1. [latex]g\left(x\right)=5x+6[/latex]
Show Solution

Increasing

  1. [latex]a\left(x\right)=5-2x[/latex]
  1. [latex]b\left(x\right)=8-3x[/latex]
Show Solution

Decreasing

  1. [latex]h\left(x\right)=-2x+4[/latex]
  1. [latex]k\left(x\right)=-4x+1[/latex]
Show Solution

Decreasing

  1. [latex]j\left(x\right)=\frac{1}{2}x-3[/latex]
  1. [latex]p\left(x\right)=\frac{1}{4}x-5[/latex]
Show Solution

Increasing

  1. [latex]n\left(x\right)=-\frac{1}{3}x-2[/latex]
  1. [latex]m\left(x\right)=-\frac{3}{8}x+3[/latex]
Show Solution

Decreasing

For the following exercises, find the slope of the line that passes through the two given points.

  1. [latex]\left(2,4\right)\,[/latex]and[latex]\,\left(4,\text{10}\right)[/latex]
  1. [latex]\left(1,\text{5}\right)\,[/latex]and[latex]\,\left(4,\text{11}\right)[/latex]
Show Solution

2

  1. [latex]\left(–1,\text{4}\right)\,[/latex]and[latex]\,\left(5,\text{2}\right)[/latex]
  1. [latex]\left(8,–2\right)\,[/latex]and[latex]\,\left(4,6\right)[/latex]
Show Solution

–2

  1. [latex]\left(6,11\right)\,[/latex]and[latex]\,\left(–4,\text{3}\right)[/latex]

For the following exercises, given each set of information, find a linear equation satisfying the conditions, if possible.

  1. [latex]f\left(-5\right)=-4,\,[/latex]and[latex]\,f\left(5\right)=2[/latex]
Show Solution

[latex]y=\frac{3}{5}x-1[/latex]

  1. [latex]f\left(-1\right)=4,\,[/latex]and[latex]\,f\left(5\right)=1[/latex]
  1. Passes through[latex]\,\left(2,4\right)\,[/latex]and[latex]\,\left(4,10\right)[/latex]
Show Solution

[latex]y=3x-2[/latex]

  1. Passes through[latex]\,\left(1,5\right)\,[/latex]and[latex]\,\left(4,11\right)[/latex]
  1. Passes through[latex]\,\left(-1,\text{4}\right)\,[/latex]and[latex]\,\left(5,\text{2}\right)[/latex]
Show Solution

[latex]y=-\frac{1}{3}x+\frac{11}{3}[/latex]

  1. Passes through[latex]\,\left(-2,\text{8}\right)\,[/latex]and[latex]\,\left(4,\text{6}\right)[/latex]
  1. x intercept at[latex]\,\left(-2,\text{0}\right)\,[/latex]and y intercept at[latex]\,\left(0,-3\right)[/latex]
Show Solution

[latex]y=-1.5x-3[/latex]

  1. x intercept at[latex]\,\left(-5,\text{0}\right)\,[/latex]and y intercept at[latex]\,\left(0,\text{4}\right)[/latex]

For the following exercises, determine whether the lines given by the equations below are parallel, perpendicular, or neither.

  1. [latex]\begin{array}{l}4x-7y=10\hfill \\ 7x+4y=1\hfill \end{array}[/latex]
Show Solution

perpendicular

  1. [latex]\begin{array}{c}3y+x=12\\ -y=8x+1\end{array}[/latex]
  1. [latex]\begin{array}{c}3y+4x=12\\ -6y=8x+1\end{array}[/latex]
Show Solution

parallel

  1. [latex]\begin{array}{l}6x-9y=10\hfill \\ 3x+2y=1\hfill \end{array}[/latex]

For the following exercises, find the x– and y-intercepts of each equation.

  1. [latex]f\left(x\right)=-x+2[/latex]
Show Solution

[latex]\begin{array}{l}f\left(0\right)=-\left(0\right)+2\\ f\left(0\right)=2\\ y-\mathrm{int}:\left(0,2\right)\\ 0=-x+2\\ x-\mathrm{int}:\left(2,0\right)\end{array}[/latex]

  1. [latex]g\left(x\right)=2x+4[/latex]
  1. [latex]h\left(x\right)=3x-5[/latex]
Show Solution

[latex]\begin{array}{l}h\left(0\right)=3\left(0\right)-5\\ h\left(0\right)=-5\\ y-\mathrm{int}:\left(0,-5\right)\\ 0=3x-5\\ x-\mathrm{int}:\left(\frac{5}{3},0\right)\end{array}[/latex]

  1. [latex]k\left(x\right)=-5x+1[/latex]
  1. [latex]-2x+5y=20[/latex]
Show Solution

[latex]\begin{array}{l}-2x+5y=20\\ -2\left(0\right)+5y=20\\ 5y=20\\ y=4\\ y-\mathrm{int}:\left(0,4\right)\\ -2x+5\left(0\right)=20\\ x=-10\\ x-\mathrm{int}:\left(-10,0\right)\end{array}[/latex]

  1. [latex]7x+2y=56[/latex]

For the following exercises, use the descriptions of each pair of lines given below to find the slopes of Line 1 and Line 2. Is each pair of lines parallel, perpendicular, or neither?

  1. Line 1: Passes through[latex]\,\left(0,6\right)\,[/latex]and[latex]\,\left(3,-24\right)[/latex]

Line 2: Passes through[latex]\,\left(-1,19\right)\,[/latex]and[latex]\,\left(8,-71\right)[/latex]

Show Solution

Line 1: m = –10 Line 2: m = –10 Parallel

  1. Line 1: Passes through[latex]\,\left(-8,-55\right)\,[/latex]and[latex]\,\left(10,89\right)[/latex]

Line 2: Passes through[latex]\,\left(9,-44\right)\,[/latex]and[latex]\,\left(4,-14\right)[/latex]

  1. Line 1: Passes through[latex]\,\left(2,3\right)\,[/latex]and[latex]\,\left(4,-1\right)[/latex]

Line 2: Passes through[latex]\,\left(6,3\right)\,[/latex]and[latex]\,\left(8,5\right)[/latex]

Show Solution

Line 1: m = –2 Line 2: m = 1 Neither

  1. Line 1: Passes through[latex]\,\left(1,7\right)\,[/latex]and[latex]\,\left(5,5\right)[/latex]

Line 2: Passes through[latex]\,\left(-1,-3\right)\,[/latex]and[latex]\,\left(1,1\right)[/latex]

  1. Line 1: Passes through[latex]\,\left(2,5\right)\,[/latex]and[latex]\,\left(5,-1\right)[/latex]

Line 2: Passes through[latex]\,\left(-3,7\right)\,[/latex]and[latex]\,\left(3,-5\right)[/latex]

Show Solution

[latex]\text{Line 1}: m=–2 \text{Line 2}: m=–2 \text{Parallel}[/latex]

For the following exercises, write an equation for the line described.

  1. Write an equation for a line parallel to[latex]\,f\left(x\right)=-5x-3\,[/latex]and passing through the point[latex]\,\left(2,\text{–}12\right).[/latex]
  1. Write an equation for a line parallel to[latex]\,g\left(x\right)=3x-1\,[/latex]and passing through the point[latex]\,\left(4,9\right).[/latex]
Show Solution

[latex]y=3x-3[/latex]

  1. Write an equation for a line perpendicular to[latex]\,h\left(t\right)=-2t+4\,[/latex]and passing through the point[latex]\,\left(-4,–1\right).[/latex]
  1. Write an equation for a line perpendicular to[latex]\,p\left(t\right)=3t+4\,[/latex]and passing through the point[latex]\,\left(3,1\right).[/latex]
Show Solution

[latex]y=-\frac{1}{3}t+2[/latex]

Graphical

For the following exercises, find the slope of the line graphed.

  1. This is a graph of a decreasing linear function on an x, y coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6.
  1. This is a graph of a function on an x, y coordinate plane. The x-axis runs from negative 6 to 6. The y-axis runs from negative 6 to 6. The lines passes through points at (0, -2) and (2, -2).

For the following exercises, write an equation for the line graphed.

  1. Graph of an increasing linear function with points at (0,1) and (3,3)
  2. Graph of a decreasing linear function with points (0,5) and (4,0)
Show Solution

[latex]y=-\frac{5}{4}x+5[/latex]

    1. Graph of a decreasing linear function with points at (0,3) and (1.5,0)
  1. Graph of an increasing linear function with points at (1,2) and (0,-1)
Show Solution

[latex]y=3x-1[/latex]

  1. Graph of a function with points at (0, 3) and (3, 3)
  1. Graph of a function with points at (0,-2.5) and (-2.5,-2.5)
Show Solution

[latex]y=-2.5[/latex]

For the following exercises, match the given linear equation with its graph in Figure 27.

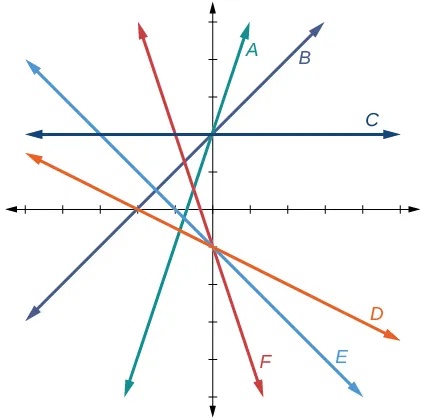
Graph of six functions where line A has a slope of 3 and y-intercept at 2, line B has a slope of 1 and y-intercept at 2, line C has a slope of 0 and y-intercept at 2, line D has a slope of -1/2 and y-intercept at -1, line E has a slope of -1 and y-intercept at -1, and line F has a slope of -2 and y-intercept at -1.
Figure 27
  1. [latex]f\left(x\right)=-x-1[/latex]
  1. [latex]f\left(x\right)=-2x-1[/latex]
Show Solution

F

  1. [latex]f\left(x\right)=-\frac{1}{2}x-1[/latex]
  1. [latex]f\left(x\right)=2[/latex]
Show Solution

C

  1. [latex]f\left(x\right)=2+x[/latex]
  1. [latex]f\left(x\right)=3x+2[/latex]
Show Solution

A

For the following exercises, sketch a line with the given features.

  1. An x-intercept of[latex]\,\left(–4,\text{0}\right)\,[/latex]and y-intercept of[latex]\,\left(0,\text{–2}\right)[/latex]
  1. An x-intercept[latex]\,\left(–2,\text{0}\right)\,[/latex]and y-intercept of[latex]\,\left(0,\text{4}\right)[/latex]
Show Solution

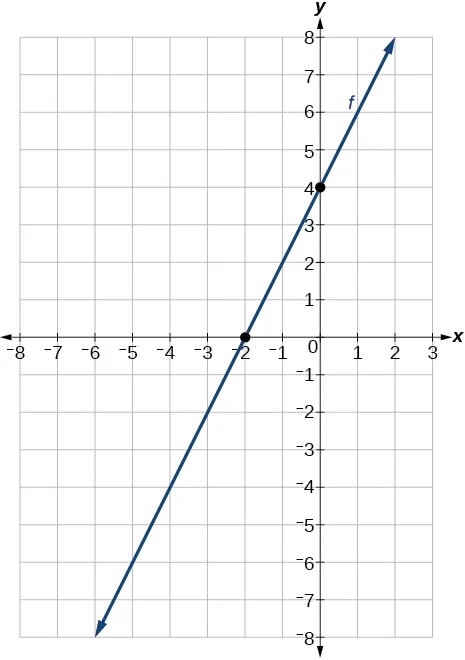
Graph of f with an x-intercept at -4 and y-intercept at -2 which gives us a slope of: 2

  1. A y-intercept of[latex]\,\left(0,\text{7}\right)\,[/latex]and slope[latex]\,-\frac{3}{2}[/latex]
  1. A y-intercept of[latex]\,\left(0,\text{3}\right)\,[/latex]and slope[latex]\,\frac{2}{5}[/latex]
Show Solution

Graph of f with an y-intercept at 3 and a slope of 2/5.

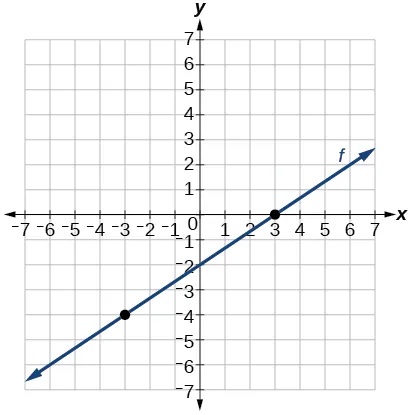
  1. Passing through the points[latex]\,\left(–6,\text{–2}\right)\,[/latex]and[latex]\,\left(6,\text{–6}\right)[/latex]
  1. Passing through the points[latex]\,\left(–3,\text{–4}\right)\,[/latex]and[latex]\,\left(3,\text{0}\right)[/latex]
Show Solution

Graph of a line that passes through the points (-3, -4) and (3, 0) which results in a slope of 2/3.

For the following exercises, sketch the graph of each equation.

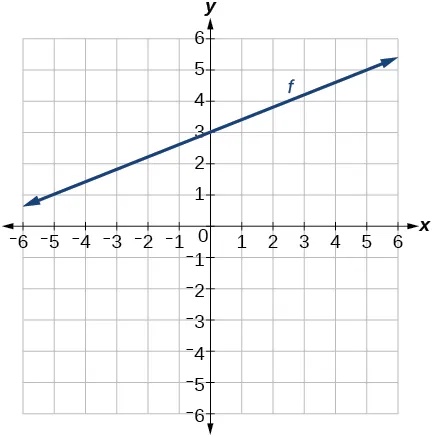
  1. [latex]f\left(x\right)=-2x-1[/latex]
  1. [latex]f\left(x\right)=-3x+2[/latex]
Show Solution

Graph of g(x) = -3x + 2 which goes through the points (0,2) and (1,-1) with a slope of -3.

  1. [latex]f\left(x\right)=\frac{1}{3}x+2[/latex]
  1. [latex]f\left(x\right)=\frac{2}{3}x-3[/latex]
Show Solution

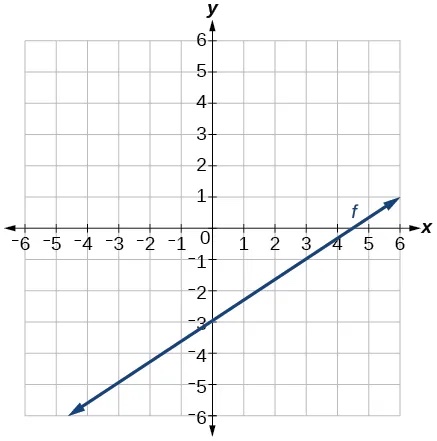
Graph of k(x) = . This line goes through the points (0,-3) and (3,-1) and has a slope of 2/3.

  1. [latex]f\left(t\right)=3+2t[/latex]
  1. [latex]p\left(t\right)=-2+3t[/latex]
Show Solution

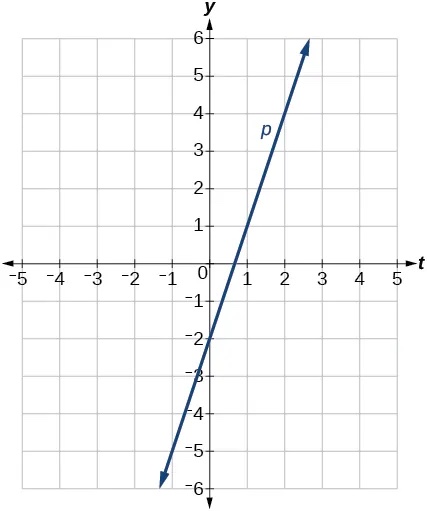
Graph of the line p(t) = 3t -2. This line goes through the points (0,-2) and (1,1) which has a slope of 3.

  1. [latex]x=3[/latex]
  1. [latex]x=-2[/latex]
Show Solution

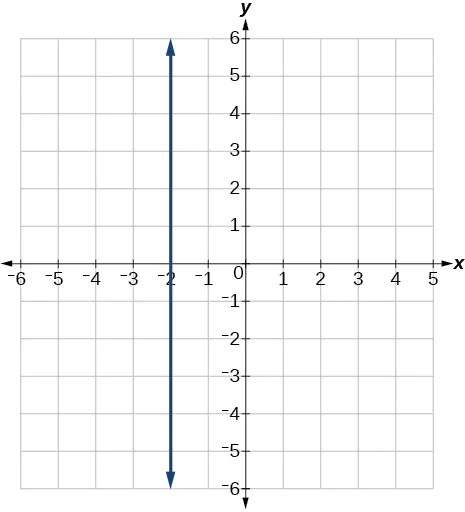
Graph of x = -2 which is a line of undefined slope that goes through the point (-2,0)

  1. [latex]r\left(x\right)=4[/latex]

For the following exercises, write the equation of the line shown in the graph.

  1. The graph of a line with a slope of 0 and y-intercept at 3.
Show Solution

[latex]y=\text{3}[/latex]

  1. Graph of a line with a slope of 0 and y-intercept at -1.
  1. Graph of a line with an undefined slope and x-intercept at -3.
Show Solution

[latex]x=-3[/latex]

  1. Graph of a line with an undefined slope and x-intercept at 2

Numeric

For the following exercises, which of the tables could represent a linear function? For each that could be linear, find a linear equation that models the data.

  1. [latex]x[/latex] 0 5 10 15
    [latex]g\left(x\right)[/latex] 5 –10 –25 –40
Show Solution

Linear,[latex]\,g\left(x\right)=-3x+5[/latex]

  1. [latex]x[/latex] 0 5 10 15
    [latex]h\left(x\right)[/latex] 5 30 105 230
  1. [latex]x[/latex] 0 5 10 15
    [latex]f\left(x\right)[/latex] –5 20 45 70
Show Solution

Linear,[latex]\,f\left(x\right)=5x-5[/latex]

  1. x 5 10 20 25
    k(x) 13 28 58 73
  1. [latex]x[/latex] 0 2 4 6
    [latex]g\left(x\right)[/latex] 6 –19 –44 –69
Show Solution

Linear,[latex]\,g\left(x\right)=-\frac{25}{2}x+6[/latex]

  1. [latex]x[/latex] 2 4 8 10
    [latex]h\left(x\right)[/latex] 13 23 43 53
  1. [latex]x[/latex] 2 4 6 8
    [latex]f\left(x\right)[/latex] –4 16 36 56
Show Solution

Linear,[latex]\,f\left(x\right)=10x-24[/latex]

  1. [latex]x[/latex] 0 2 6 8
    [latex]k\left(x\right)[/latex] 6 31 106 231

Technology

For the following exercises, use a calculator or graphing technology to complete the task.

  1. If[latex]\,f\,[/latex]is a linear function,[latex]\,f\left(0.1\right)=11.5, \text{and} f\left(0.4\right)=–5.9,\,[/latex]find an equation for the function.
Show Solution

[latex]f\left(x\right)=-58x+17.3[/latex]

  1. Graph the function[latex]\,f\,[/latex]on a domain of[latex]\,\left[–10,10\right]:f\left(x\right)=0.02x-0.01.\,[/latex]Enter the function in a graphing utility. For the viewing window, set the minimum value of[latex]\,x\,[/latex]to be[latex]\,-10\,[/latex]and the maximum value of[latex]\,x\,[/latex]to be[latex]\,10.[/latex]
  1. Graph the function[latex]\,f\,[/latex]on a domain of[latex]\,\left[–10,10\right]:fx)=2,500x+4,000[/latex]
Show Solution

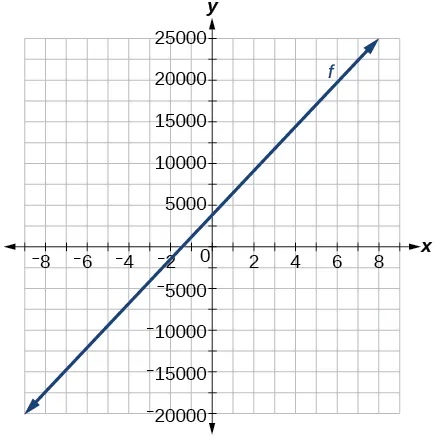
Graph of f(x) = 2500x + 4000

  1. The table below shows the input,[latex]\,w,[/latex] and output,[latex]\,k,[/latex] for a linear function[latex]\,k.\,[/latex]a. Fill in the missing values of the table. b. Write the linear function[latex]\,k,[/latex] rounded to 3 decimal places.
w –10 5.5 67.5 b
k 30 –26 a –44
  1. The table below shows the input,[latex]\,p,[/latex] and output,[latex]\,q,[/latex] for a linear function[latex]\,q.\,[/latex]a. Fill in the missing values of the table. b. Write the linear function[latex]\,k.[/latex]
p 0.5 0.8 12 b
q 400 700 a 1,000,000
Show Solution

a. [latex]a=11,900[/latex] and [latex]b=1000.1[/latex]

b. [latex]𝑞(𝑝)=1000𝑝–100[/latex]

  1. Graph the linear function[latex]\,f\,[/latex]on a domain of[latex]\,\left[-10,10\right]\,[/latex]for the function whose slope is[latex]\,\frac{1}{8}\,[/latex]and y-intercept is[latex]\,\frac{31}{16}.\,[/latex]Label the points for the input values of[latex]\,-10\,[/latex]and[latex]\,10.[/latex]
  1. Graph the linear function[latex]\,f\,[/latex]on a domain of[latex]\,\left[-0.1,0.1\right]\,[/latex]for the function whose slope is 75 and y-intercept is[latex]\,-22.5.\,[/latex]Label the points for the input values of[latex]\,-0.1\,[/latex]and[latex]\,0.1.[/latex]
Show Solution

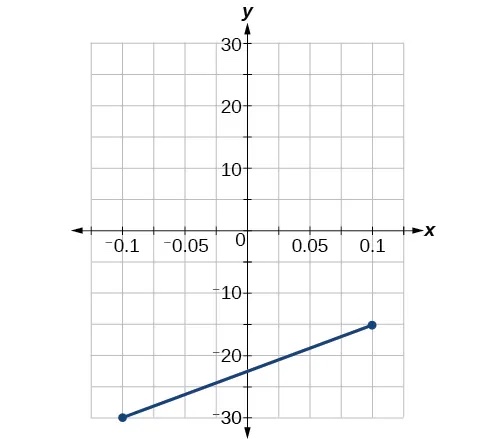
Graph of a line with endpoints at (-10, 0.6875) and (10, 3.1875).

  1. Graph the linear function[latex]\,f\,[/latex]where[latex]\,f\left(x\right)=ax+b\,[/latex]on the same set of axes on a domain of[latex]\,\left[-4,4\right]\,[/latex]for the following values of[latex]\,a\,[/latex]and[latex]\,b.[/latex]
  1. [latex]a=2;b=3[/latex]
  2. [latex]a=2;b=4[/latex]
  3. [latex]a=2;b=–4[/latex]
  4. [latex]a=2;b=–5[/latex]

Extensions

  1. Find the value of[latex]\,x\,[/latex]if a linear function goes through the following points and has the following slope:[latex]\,\left(x,2\right),\left(-4,6\right),\,m=3[/latex]
  1. Find the value of y if a linear function goes through the following points and has the following slope:[latex]\,\left(10,y\right),\left(25,100\right),\,m=-5[/latex]
Show Solution

y = 175

  1. Find the equation of the line that passes through the following points:

[latex]\,\left(a,\text{ }b\right)\,[/latex]and[latex]\,\left(a,\text{ }b+1\right)[/latex]

  1. Find the equation of the line that passes through the following points:

[latex]\left(2a,b\right)\,[/latex]and[latex]\,\left(a,b+1\right)[/latex]

  1. Find the equation of the line that passes through the following points:

[latex]\left(a,0\right)[/latex]and[latex]\,\left(c,d\right)[/latex]

  1. Find the equation of the line parallel to the line[latex]\,g\left(x\right)=-0.\text{01}x\text{+2}\text{.01}\,[/latex]through the point[latex]\,\left(1,\text{2}\right).[/latex]
  1. Find the equation of the line perpendicular to the line[latex]\,g\left(x\right)=-0.\text{01}x\text{+2}\text{.01}\,[/latex]through the point[latex]\,\left(1,\text{2}\right).[/latex]

For the following exercises, use the functions[latex]\,f\left(x\right)=-0.\text{1}x\text{+200 and }g\left(x\right)=20x+0.1.[/latex]

  1. Find the point of intersection of the lines[latex]\,f\,[/latex]and[latex]\,g.[/latex]
Show Solution

[latex]\text{ }\left(\frac{1999}{201},\frac{400,001}{2010}\right)[/latex]

  1. Where is[latex]\,f\left(x\right)\,[/latex]greater than[latex]\,g\left(x\right)?\,[/latex]Where is[latex]\,g\left(x\right)\,[/latex]greater than[latex]\,f\left(x\right)?[/latex]

Real-World Applications

  1. At noon, a barista notices that she has $20 in her tip jar. If she makes an average of $0.50 from each customer, how much will she have in her tip jar if she serves[latex]\,n\,[/latex]more customers during her shift?
Show Solution

[latex]20+0.5n[/latex]

  1. A gym membership with two personal training sessions costs $125, while gym membership with five personal training sessions costs $260. What is cost per session?
  1. A clothing business finds there is a linear relationship between the number of shirts,[latex]\,n,[/latex] it can sell and the price,[latex]\,p,[/latex] it can charge per shirt. In particular, historical data shows that 1,000 shirts can be sold at a price of[latex]\,$30,[/latex] while 3,000 shirts can be sold at a price of $22. Find a linear equation in the form[latex]\,p\left(n\right)=mn+b\,[/latex]that gives the price[latex]\,p\,[/latex]they can charge for[latex]\,n\,[/latex]shirts.
Show Solution

[latex]p\left(n\right)=-0.004n+34[/latex]

  1. A phone company charges for service according to the formula [latex]\,C\left(n\right)=24+0.1n,[/latex]where[latex]\,n\,[/latex]is the number of minutes talked, and[latex]\,C\left(n\right)\,[/latex]is the monthly charge, in dollars. Find and interpret the rate of change and initial value.
  1. A farmer finds there is a linear relationship between the number of bean stalks,[latex]\,n,[/latex]she plants and the yield,[latex]\,y,[/latex]each plant produces. When she plants 30 stalks, each plant yields 30 oz of beans. When she plants 34 stalks, each plant produces 28 oz of beans. Find a linear relationship in the form[latex]\,y=mn+b\,[/latex]that gives the yield when[latex]\,n\,[/latex]stalks are planted.
Show Solution

[latex]y=-0.5n+45[/latex]

  1. A city’s population in the year 1960 was 287,500. In 1989 the population was 275,900. Compute the rate of growth of the population and make a statement about the population rate of change in people per year.
  1. A town’s population has been growing linearly. In 2003, the population was 45,000, and the population has been growing by 1,700 people each year. Write an equation,[latex]\,P\left(t\right),[/latex]for the population[latex]\,t\,[/latex]years after 2003.
Show Solution

[latex]P\left(t\right)=1700t+45,000[/latex]

  1. Suppose that average annual income (in dollars) for the years 1990 through 1999 is given by the linear function:[latex]\,I\left(x\right)=1054x+23,286,[/latex] where[latex]\,x\,[/latex]is the number of years after 1990. Which of the following interprets the slope in the context of the problem?
  1. As of 1990, average annual income was $23,286.
  2. In the ten-year period from 1990–1999, average annual income increased by a total of $1,054.
  3. Each year in the decade of the 1990s, average annual income increased by $1,054.
  4. Average annual income rose to a level of $23,286 by the end of 1999.
  1. When the temperature is 0 degrees Celsius, the Fahrenheit temperature is 32. When the Celsius temperature is 100, the corresponding Fahrenheit temperature is 212. Express the Fahrenheit temperature as a linear function of[latex]\,C,[/latex] the Celsius temperature,[latex]\,F\left(C\right).[/latex]
  1. Find the rate of change of Fahrenheit temperature for each unit change temperature of Celsius.
  2. Find and interpret[latex]\,F\left(28\right).[/latex]
  3. Find and interpret[latex]\,F\left(–40\right).[/latex]
Show Solution
  1. [latex]\text{Rate of change =}\frac{\Delta F}{\Delta C}=\frac{212-32}{100-0}=1.8\text{ degrees F for one degree change in C}[/latex]
  2. [latex]F\left(28\right)=1.8\left(28\right)+32=82.4\text{ degrees F is 28 degrees C}[/latex]
  3. [latex]F\left(-40\right)=1.8\left(-40\right)+32=-40\text{ degrees F is -40 degrees C}[/latex]

Glossary

decreasing linear function
a function with a negative slope: If[latex]\,f\left(x\right)=mx+b, \text{then} m0.[/latex]
horizontal line
a line defined by[latex]\,f\left(x\right)=b,[/latex]where[latex]\,b\,[/latex]is a real number. The slope of a horizontal line is 0.
increasing linear function
a function with a positive slope: If[latex]\,f\left(x\right)=mx+b, \text{then} m>0.[/latex]
linear function
a function with a constant rate of change that is a polynomial of degree 1, and whose graph is a straight line
parallel lines
two or more lines with the same slope
perpendicular lines
two lines that intersect at right angles and have slopes that are negative reciprocals of each other
point-slope form
the equation for a line that represents a linear function of the form[latex]\,y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex]
slope
the ratio of the change in output values to the change in input values; a measure of the steepness of a line
slope-intercept form
the equation for a line that represents a linear function in the form[latex]\,f\left(x\right)=mx+b[/latex]
vertical line
a line defined by[latex]\,x=a,[/latex] where[latex]\,a\,[/latex]is a real number. The slope of a vertical line is undefined.

Media Attributions

  1. http://www.chinahighlights.com/shanghai/transportation/maglev-train.htm ↵
  2. https://www.cbsnews.com/news/teens-are-sending-60-texts-a-day-study-says/ ↵

License

Icon for the Creative Commons Attribution 4.0 International License

College Algebra Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book