Chapter 6 Exponential and Logarithmic Functions

6.4 Graphs of Logarithmic Functions

Learning Objectives

In this section, you will:

  • Identify the domain of a logarithmic function.
  • Graph logarithmic functions.
  • Graph transformations of logarithmic functions.

In Section 6.2, Graphs of Exponential Functions, we saw how creating a graphical representation of an exponential model gives us another layer of insight for predicting future events. How do logarithmic graphs give us insight into situations? Because every logarithmic function is the inverse function of an exponential function, we can think of every output on a logarithmic graph as the input for the corresponding inverse exponential equation. In other words, logarithms give the cause for an effect.

To illustrate, suppose we invest[latex]\,\text{\$}2500\,[/latex]in an account that offers an annual interest rate of[latex]\,5[/latex]% compounded continuously. We already know that the balance in our account for any year[latex]\,t\,[/latex]can be found with the equation[latex]\,A=2500{e}^{0.05t}.[/latex]

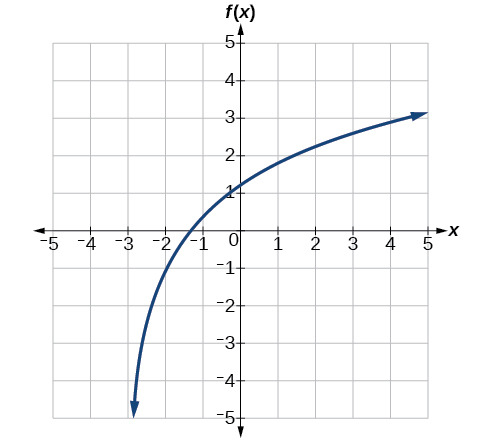
But what if we wanted to know the year for any balance? We would need to create a corresponding new function by interchanging the input and the output; thus we would need to create a logarithmic model for this situation. By graphing the model, we can see the output (year) for any input (account balance). For instance, what if we wanted to know how many years it would take for our initial investment to double? Figure 1 shows this point on the logarithmic graph.

 

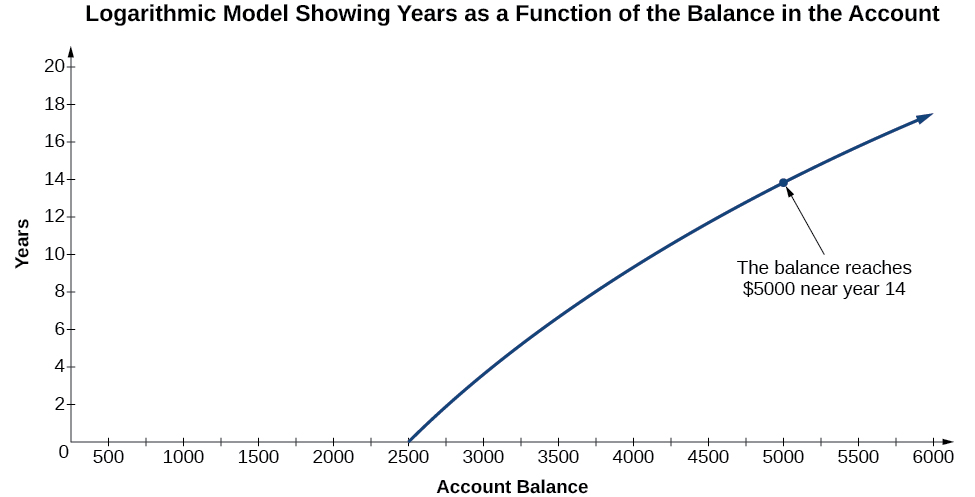
A graph titled, “Logarithmic Model Showing Years as a Function of the Balance in the Account”. The x-axis is labeled, “Account Balance”, and the y-axis is labeled, “Years”. The line starts at $25,000 on the first year. The graph also notes that the balance reaches $5,000 near year 14.
Figure 1

In this section, we will discuss the values for which a logarithmic function is defined and then turn our attention to graphing the family of logarithmic functions.

Identify the Domain of a Logarithmic Function

Before working with graphs, we will take a look at the domain (the set of input values) for which the logarithmic function is defined.

Recall that the exponential function is defined as[latex]\,y={b}^{x}\,[/latex]for any real number[latex]\,x\,[/latex]and constant[latex]\,b>0,[/latex] [latex]b\ne 1,[/latex] where

  • The domain of[latex]\,y\,[/latex]is[latex]\,\left(-\infty ,\infty \right).[/latex]
  • The range of[latex]\,y\,[/latex]is[latex]\,\left(0,\infty \right).[/latex]

In the last section we learned that the logarithmic function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]is the inverse of the exponential function[latex]\,y={b}^{x}.\,[/latex]So, as inverse functions:

  • The domain of[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]is the range of[latex]\,y={b}^{x}:\,[/latex][latex]\left(0,\infty \right).[/latex]
  • The range of[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]is the domain of[latex]\,y={b}^{x}:\,[/latex][latex]\left(-\infty ,\infty \right).[/latex]

Transformations of the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]behave similarly to those of other functions. Just as with other parent functions, we can apply the four types of transformations—shifts, stretches, compressions, and reflections—to the parent function without loss of shape.

In Graphs of Exponential Functions we saw that certain transformations can change the range of[latex]\,y={b}^{x}.\,[/latex]Similarly, applying transformations to the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]can change the domain. When finding the domain of a logarithmic function, therefore, it is important to remember that the domain consists only of positive real numbers. That is, the argument of the logarithmic function must be greater than zero.

For example, consider[latex]\,f\left(x\right)={\mathrm{log}}_{4}\left(2x-3\right).\,[/latex]This function is defined for any values of[latex]\,x\,[/latex]such that the argument, in this case[latex]\,2x-3,[/latex] is greater than zero. To find the domain, we set up an inequality and solve for[latex]\,x:[/latex]

[latex]\begin{array}{ll}2x-3>0\hfill & \text{Show the argument greater than zero}.\hfill \\ \,\,\,\,\,\,\,\,\,\,2x>3\hfill & \text{Add 3}.\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,x>1.5\begin{array}{cccc}& & & \end{array}\hfill & \text{Divide by 2}.\hfill \end{array}[/latex]

In interval notation, the domain of[latex]\,f\left(x\right)={\mathrm{log}}_{4}\left(2x-3\right)\,[/latex]is[latex]\,\left(1.5,\infty \right).[/latex]

HOW TO

Given a logarithmic function, identify a domain.

  1. Set up an inequality showing the argument greater than zero.
  2. Solve for[latex]\,x.[/latex]
  3. Write the domain in interval notation.

 

Identifying the Domain of a Logarithmic Shift

What is the domain of[latex]\,f\left(x\right)={\mathrm{log}}_{2}\left(x+3\right)?[/latex]

Show Solution

The logarithmic function is defined only when the input is positive, so this function is defined when[latex]\,x+3>0.\,[/latex]Solving this inequality,

[latex]\begin{array}{ll}x+3>0\hfill & \text{The input must be positive}.\hfill \\ \,\,\,\,\,\,\,\,\,\,x>-3\begin{array}{cccc}& & & \end{array}\hfill & \text{Subtract 3}.\hfill \end{array}[/latex]

The domain of[latex]\,f\left(x\right)={\mathrm{log}}_{2}\left(x+3\right)\,[/latex]is[latex]\,\left(-3,\infty \right).[/latex]

Try It

What is the domain of[latex]\,f\left(x\right)={\mathrm{log}}_{5}\left(x-2\right)+1?[/latex]

Show Solution

[latex]\left(2,\infty \right)[/latex]

Identifying the Domain of a Logarithmic Shift and Reflection

What is the domain of f(x ) = log (5 – 2x)?

Show Solution

The logarithmic function is defined only when the input is positive, so this function is defined when 5 – 2x [latex]\gt[/latex] 0; solving this inequality,

5 – 2x [latex]\gt[/latex] 0 The input must be positive.
– 2x [latex]\gt[/latex] -5 Subtract 5.
x [latex]\lt[/latex]  [latex]\frac{5}{2}[/latex] Divide by -2 and switch the inequality.

The domain of f(x ) = log (5 – 2x) is [latex]\,\left(–\infty ,\frac{5}{2}\right).[/latex]

Try It

What is the domain of[latex]\,f\left(x\right)=\mathrm{log}\left(x-5\right)+2?[/latex]

Show Solution

[latex]\left(5,\infty \right)[/latex]

Graphing Logarithmic Functions

Now that we have a feel for the set of values for which a logarithmic function is defined, we move on to graphing logarithmic functions. The family of logarithmic functions includes the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]along with all its transformations: shifts, stretches, compressions, and reflections.

We begin with the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right).\,[/latex]Because every logarithmic function of this form is the inverse of an exponential function with the form[latex]\,y={b}^{x},[/latex] their graphs will be reflections of each other across the line[latex]\,y=x.\,[/latex]To illustrate this, we can observe the relationship between the input and output values of[latex]\,y={2}^{x}\,[/latex]and its equivalent[latex]\,x={\mathrm{log}}_{2}\left(y\right)\,[/latex]in Table 1.

[latex]x[/latex] [latex]-3[/latex] [latex]-2[/latex] [latex]-1[/latex] [latex]0[/latex] [latex]1[/latex] [latex]2[/latex] [latex]3[/latex]
[latex]{2}^{x}=y[/latex] [latex]\frac{1}{8}[/latex] [latex]\frac{1}{4}[/latex] [latex]\frac{1}{2}[/latex] [latex]1[/latex] [latex]2[/latex] [latex]4[/latex] [latex]8[/latex]
[latex]{\mathrm{log}}_{2}\left(y\right)=x[/latex] [latex]-3[/latex] [latex]-2[/latex] [latex]-1[/latex] [latex]0[/latex] [latex]1[/latex] [latex]2[/latex] [latex]3[/latex]

Table 1

Using the inputs and outputs from Table 1, we can build another table to observe the relationship between points on the graphs of the inverse functions[latex]\,f\left(x\right)={2}^{x}\,[/latex]and[latex]\,g\left(x\right)={\mathrm{log}}_{2}\left(x\right).\,[/latex]

[latex]f\left(x\right)={2}^{x}[/latex] [latex]\left(-3,\frac{1}{8}\right)[/latex] [latex]\left(-2,\frac{1}{4}\right)[/latex] [latex]\left(-1,\frac{1}{2}\right)[/latex] [latex]\left(0,1\right)[/latex] [latex]\left(1,2\right)[/latex] [latex]\left(2,4\right)[/latex] [latex]\left(3,8\right)[/latex]
[latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex] [latex]\left(\frac{1}{8},-3\right)[/latex] [latex]\left(\frac{1}{4},-2\right)[/latex] [latex]\left(\frac{1}{2},-1\right)[/latex] [latex]\left(1,0\right)[/latex] [latex]\left(2,1\right)[/latex] [latex]\left(4,2\right)[/latex] [latex]\left(8,3\right)[/latex]

Table 2

As expected, the x– and y-coordinates are reversed for the inverse functions. Figure 2 shows the graph of[latex]\,f\,[/latex]and[latex]\,g.[/latex]

 

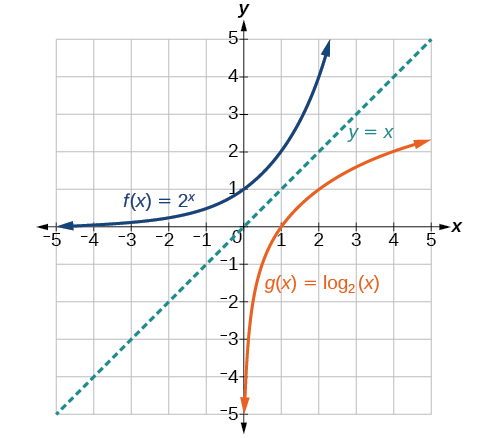
Graph of two functions, f(x)=2^x and g(x)=log_2(x), with the line y=x denoting the axis of symmetry.
Figure 2
Notice that the graphs of f(x)=2^x and g(x)=log2(x) are reflections about the line y=x.

Observe the following from the graph:

  • [latex]f\left(x\right)={2}^{x}\,[/latex]has a y-intercept at[latex]\,\left(0,1\right)\,[/latex]and[latex]\,g\left(x\right)={\mathrm{log}}_{2}\left(x\right)\,[/latex]has an x– intercept at[latex]\,\left(1,0\right).[/latex]
  • The domain of[latex]\,f\left(x\right)={2}^{x},[/latex] [latex]\left(-\infty ,\infty \right),[/latex] is the same as the range of[latex]\,g\left(x\right)={\mathrm{log}}_{2}\left(x\right).[/latex]
  • The range of[latex]\,f\left(x\right)={2}^{x},[/latex] [latex]\left(0,\infty \right),[/latex] is the same as the domain of[latex]\,g\left(x\right)={\mathrm{log}}_{2}\left(x\right).[/latex]

 

Characteristics of the Graph of the Parent Function, f(x) = logb(x)

For any real number[latex]\,x\,[/latex]and constant[latex]\,b>0,[/latex][latex]b\ne 1,[/latex] we can see the following characteristics in the graph of[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right):[/latex]

  • one-to-one function
  • vertical asymptote:[latex]\,x=0[/latex]
  • domain:[latex]\,\left(0,\infty \right)[/latex]
  • range:[latex]\,\left(-\infty ,\infty \right)[/latex]
  • x-intercept:[latex]\,\left(1,0\right)\,[/latex]and key point [latex]\left(b,1\right)[/latex]
  • y-intercept: none
  • increasing if[latex]\,b>1[/latex]
  • decreasing if [latex]0 \lt b \lt 1[/latex]

See Figure 3.

 

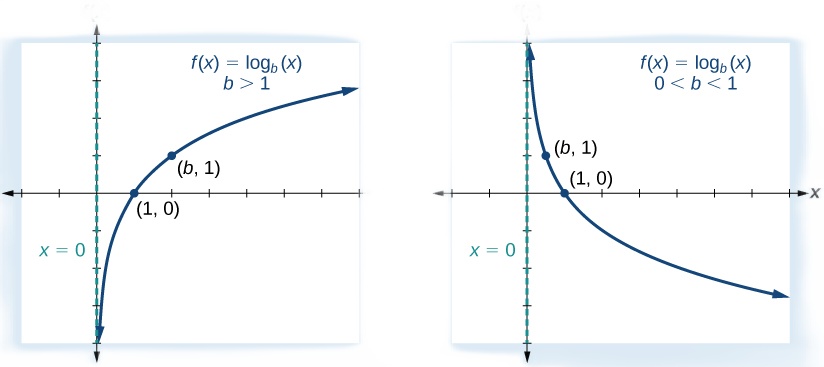
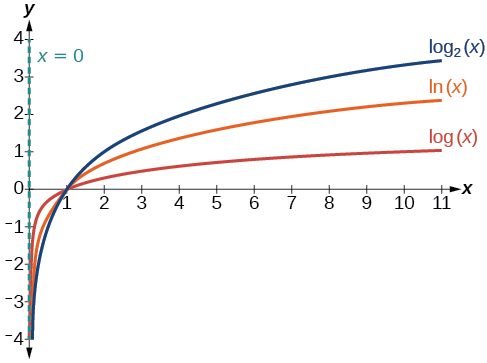
Two graphs of the function f(x)=log_b(x) with points (1,0) and (b, 1). The first graph shows the line when b>1, and the second graph shows the line when 0
Figure 3

 

Figure 4 shows how changing the base[latex]\,b\,[/latex]in[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]can affect the graphs. Observe that the graphs compress vertically as the value of the base increases. (Note: recall that the function[latex]\,\mathrm{ln}\left(x\right)\,[/latex]has base[latex]\,e\approx \text{2}.\text{718.)}[/latex]

 

Two graphs of the function f(x)=log_b(x) with points (1,0) and (b, 1). The first graph shows the line when b>1, and the second graph shows the line when 0
Figure 4

How To

Given a logarithmic function with the form[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right),[/latex] graph the function.

  1. Draw and label the vertical asymptote,[latex]\,x=0.[/latex]
  2. Plot the x-intercept,[latex]\,\left(1,0\right).[/latex]
  3. Plot the key point[latex]\,\left(b,1\right).[/latex]
  4. Draw a smooth curve through the points.
  5. State the domain,[latex]\,\left(0,\infty \right),[/latex] the range,[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote,[latex]\,x=0.[/latex]

Graphing a Logarithmic Function with the Form f(x) = logb(x).

Graph[latex]\,f\left(x\right)={\mathrm{log}}_{5}\left(x\right).\,[/latex]State the domain, range, and asymptote.

Show Solution

Before graphing, identify the behavior and key points for the graph.

  • Since[latex]\,b=5\,[/latex]is greater than one, we know the function is increasing. The left tail of the graph will approach the vertical asymptote[latex]\,x=0,[/latex] and the right tail will increase slowly without bound.
  • The x-intercept is[latex]\,\left(1,0\right).[/latex]
  • The key point[latex]\,\left(5,1\right)\,[/latex]is on the graph.
  • We draw and label the asymptote, plot and label the points, and draw a smooth curve through the points (see Figure 5).
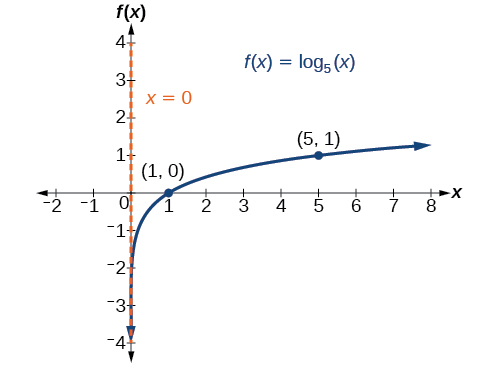
Graph of f(x)=log_5(x) with labeled points at (1, 0) and (5, 1). The y-axis is the asymptote.
Figure 5

The domain is[latex]\,\left(0,\infty \right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=0.[/latex]

Try It

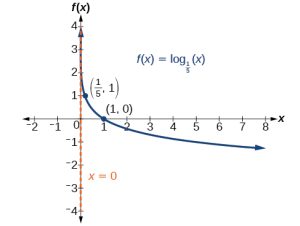
Graph[latex]\,f\left(x\right)={\mathrm{log}}_{\frac{1}{5}}\left(x\right).\,[/latex]State the domain, range, and asymptote.

Show Solution

 

Graph of f(x)=log(1/5)(x)
Figure 6

 

The domain is[latex]\,\left(0,\infty \right),[/latex]the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=0.[/latex]

 

Given f(x) = log3(x – 2) + 1

Graphing Transformations of Logarithmic Functions

As we mentioned in the beginning of the section, transformations of logarithmic graphs behave similarly to those of other parent functions. We can shift, stretch, compress, and reflect the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]without loss of shape.

Graphing a Horizontal Shift of f(x) = logb(x)

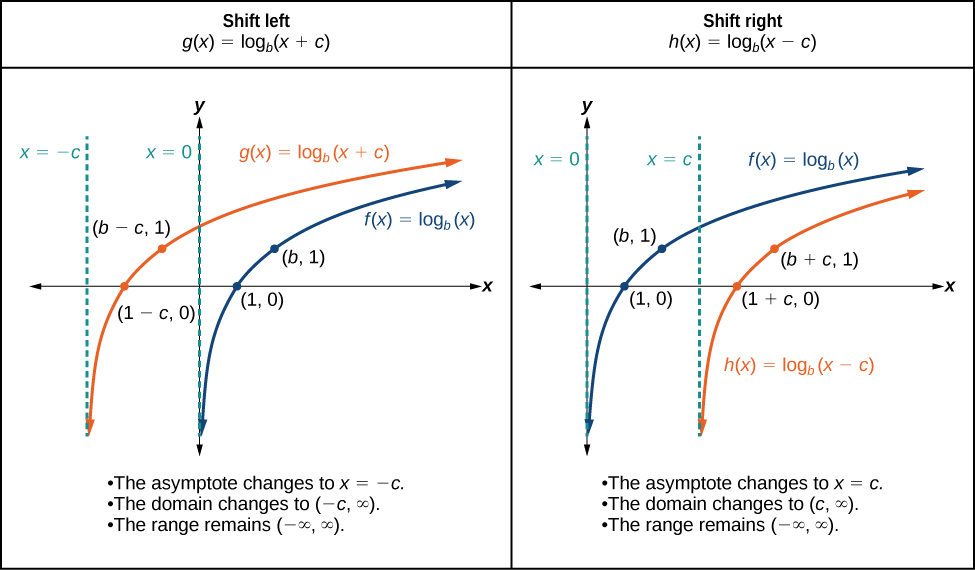
When a constant[latex]\,c\,[/latex]is added to the input of the parent function[latex]\,f\left(x\right)=lo{g}_{b}\left(x\right),[/latex] the result is a horizontal shift[latex]\,c\,[/latex]units in the opposite direction of the sign on[latex]\,c.\,[/latex]To visualize horizontal shifts, we can observe the general graph of the parent function[latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]and for[latex]\,c>0\,[/latex]alongside the shift left,[latex]\,g\left(x\right)={\mathrm{log}}_{b}\left(x+c\right),[/latex] and the shift right,[latex]\,h\left(x\right)={\mathrm{log}}_{b}\left(x-c\right).[/latex] See Figure 7.

 

Graph of two functions. The parent function is f(x)=log_b(x), with an asymptote at x=0 and g(x)=log_b(x+c) is the translation function with an asymptote at x=-c. This shows the translation of shifting left.
Figure 7

Horizontal Shifts of the Parent Function y = logb(x)

For any constant[latex]\,c,[/latex] the function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x+c\right)[/latex]

  • shifts the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]left[latex]\,c\,[/latex]units if [latex]c  > 0[/latex].
  • shifts the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]right[latex]\,c\,[/latex]units if [latex]c \lt 0[/latex].
  • has the vertical asymptote[latex]\,x=-c.[/latex]
  • has domain[latex]\,\left(-c,\infty \right).[/latex]
  • has range[latex]\,\left(-\infty ,\infty \right).[/latex]

How To

Given a logarithmic function with the form[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x+c\right),[/latex] graph the translation.

  1. Identify the horizontal shift:
    1. If[latex]\,c>0,[/latex] shift the graph of[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]left[latex]\,c\,[/latex]units.
    2. If[latex]\,c \lt 0,[/latex] shift the graph of[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]right[latex]\,c\,[/latex]units.
  2. Draw the vertical asymptote[latex]\,x=-c.[/latex]
  3. Identify three key points from the parent function. Find new coordinates for the shifted functions by subtracting[latex]\,c\,[/latex]from the[latex]\,x\,[/latex]coordinate.
  4. Label the three points.
  5. The domain is[latex]\,\left(-c,\infty \right),[/latex]the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=-c.[/latex]

Graphing a Horizontal Shift of the Parent Function y = logb(x)

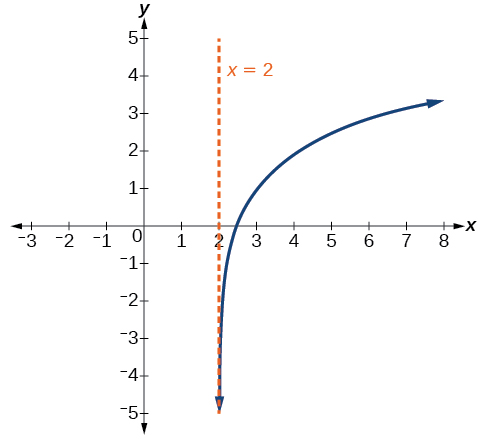
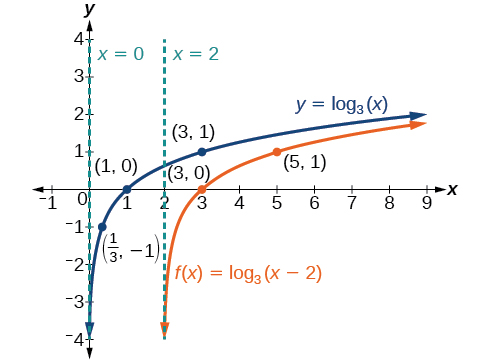
Sketch the horizontal shift[latex]\,f\left(x\right)={\mathrm{log}}_{3}\left(x-2\right)\,[/latex]alongside its parent function. Include the key points and asymptotes on the graph. State the domain, range, and asymptote.

Show Solution

Since the function is[latex]\,f\left(x\right)={\mathrm{log}}_{3}\left(x-2\right),[/latex] we notice[latex]\,x+\left(-2\right)=x–2.[/latex]

Thus[latex]\,c=-2,[/latex]so[latex]\,c \lt 0.\,[/latex]This means we will shift the function[latex]\,f\left(x\right)={\mathrm{log}}_{3}\left(x\right)\,[/latex]right 2 units.

The vertical asymptote is[latex]\,x=-\left(-2\right)\,[/latex]or[latex]\,x=2.[/latex]

Consider the three key points from the parent function,[latex]\,\left(\frac{1}{3},-1\right),[/latex][latex]\left(1,0\right),[/latex]and[latex]\,\left(3,1\right).[/latex]

The new coordinates are found by adding 2 to the[latex]\,x\,[/latex]coordinates.

Label the points[latex]\,\left(\frac{7}{3},-1\right),[/latex][latex]\left(3,0\right),[/latex] and[latex]\,\left(5,1\right).[/latex]

The domain is[latex]\,\left(2,\infty \right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=2.[/latex]

Graph of two functions. The parent function is y=log_3(x), with an asymptote at x=0 and labeled points at (1/3, -1), (1, 0), and (3, 1).The translation function f(x)=log_3(x-2) has an asymptote at x=2 and labeled points at (3, 0) and (5, 1).
Figure 8

Try It

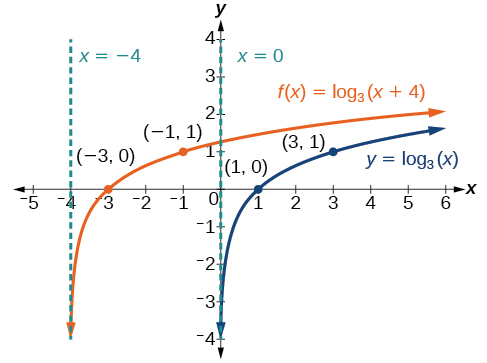
Sketch a graph of[latex]\,f\left(x\right)={\mathrm{log}}_{3}\left(x+4\right)\,[/latex]alongside its parent function. Include the key points and asymptotes on the graph. State the domain, range, and asymptote.

Show Solution
Graph of two functions. The parent function is y=log_3(x), with an asymptote at x=0 and labeled points at (1, 0), and (3, 1).The translation function f(x)=log_3(x+4) has an asymptote at x=-4 and labeled points at (-3, 0) and (-1, 1).
Figure 9

 

The domain is[latex]\,\left(-4,\infty \right),[/latex] the range[latex]\,\left(-\infty ,\infty \right),[/latex] and the asymptote[latex]\,x=–4.[/latex]

 

 

Graphing a Vertical Shift of y = logb(x)

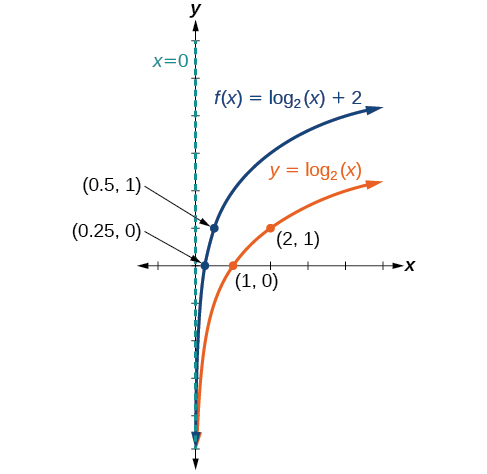
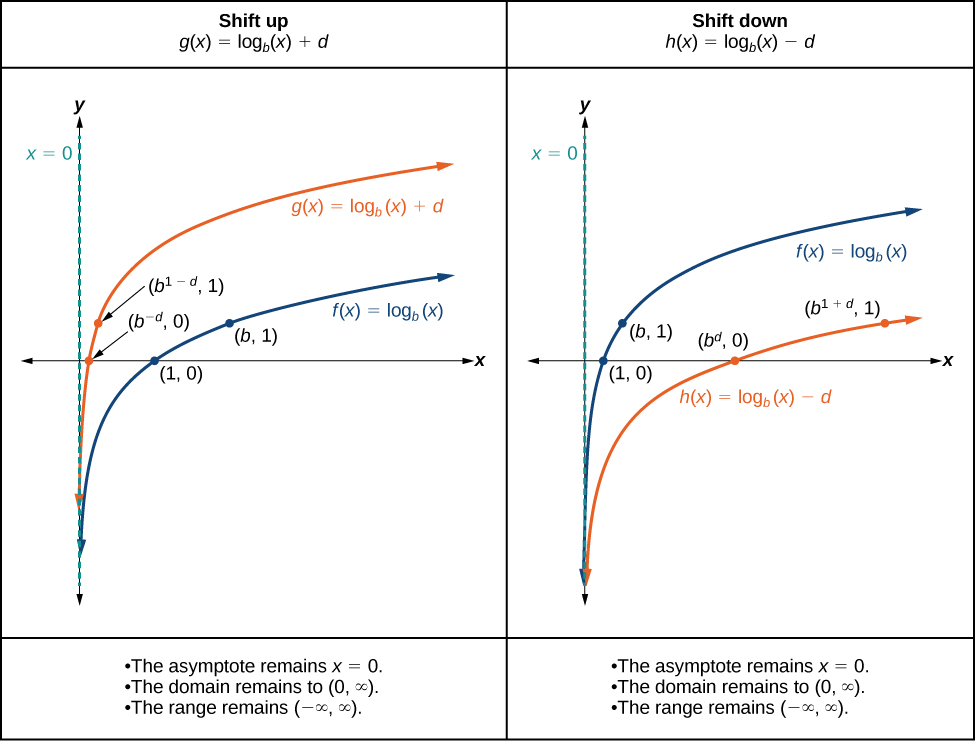
When a constant[latex]\,d\,[/latex]is added to the parent function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right),[/latex] the result is a vertical shift[latex]\,d\,[/latex]units in the direction of the sign on[latex]\,d.\,[/latex]To visualize vertical shifts, we can observe the general graph of the parent function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]alongside the shift up,[latex]\,g\left(x\right)={\mathrm{log}}_{b}\left(x\right)+d\,[/latex], and the shift down,[latex]\,h\left(x\right)={\mathrm{log}}_{b}\left(x\right)-d.[/latex] (See Figure 10)

 

Graph of two functions. The parent function is f(x)=log_b(x), with an asymptote at x=0 and g(x)=log_b(x)+d is the translation function with an asymptote at x=0. This shows the translation of shifting up. Graph of two functions. The parent function is f(x)=log_b(x), with an asymptote at x=0 and g(x)=log_b(x)-d is the translation function with an asymptote at x=0. This shows the translation of shifting down.
Figure 10

Vertical Shifts of the Parent Function y = logb(x)

For any constant[latex]\,d,[/latex] the function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)+d[/latex]

  • shifts the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]up[latex]\,d\,[/latex]units if d > 0.
  • shifts the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]down[latex]\,d\,[/latex]units if d < 0.
  • has the vertical asymptote[latex]\,x=0.[/latex]
  • has domain[latex]\,\left(0,\infty \right).[/latex]
  • has range[latex]\,\left(-\infty ,\infty \right).[/latex]

How To

Given a logarithmic function with the form[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)+d,[/latex] graph the translation.

  1. Identify the vertical shift:
    • If d > 0 shift the graph of[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]up[latex]\,d\,[/latex] units.
    • If d < 0 shift the graph of[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex]down[latex]\,d\,[/latex] units.
  2. Draw the vertical asymptote[latex]\,x=0.[/latex]
  3. Identify three key points from the parent function. Find new coordinates for the shifted functions by adding[latex]\,d\,[/latex]to the[latex]\,y\,[/latex]coordinate.
  4. Label the three points.
  5. The domain is[latex]\,\left(0,\infty \right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=0.[/latex]

Graphing a Vertical Shift of the Parent Function y = logb(x)

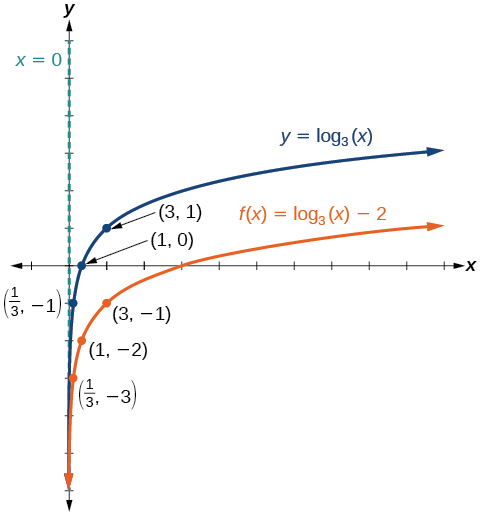
Sketch a graph of[latex]\,f\left(x\right)={\mathrm{log}}_{3}\left(x\right)-2\,[/latex]alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

Show Solution

Since the function is[latex]\,f\left(x\right)={\mathrm{log}}_{3}\left(x\right)-2,[/latex]we will notice[latex]\,d=–2.\,[/latex]Thus[latex]\,d0.[/latex] This means we will shift the function[latex]\,f\left(x\right)={\mathrm{log}}_{3}\left(x\right)\,[/latex]down 2 units. The vertical asymptote is[latex]\,x=0.[/latex] Consider the three key points from the parent function,[latex]\,\left(\frac{1}{3},-1\right),[/latex][latex]\left(1,0\right),[/latex]and[latex]\,\left(3,1\right).[/latex] The new coordinates are found by subtracting 2 from the y coordinates.

Label the points[latex]\,\left(\frac{1}{3},-3\right),[/latex][latex]\left(1,-2\right),[/latex] and[latex]\,\left(3,-1\right).[/latex]

The domain is[latex]\,\left(0,\infty \right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=0.[/latex]

 

Graph of two functions. The parent function is f(x)=log_b(x), with an asymptote at x=0 and g(x)=log_b(x)+d is the translation function with an asymptote at x=0. This shows the translation of shifting up. Graph of two functions. The parent function is f(x)=log_b(x), with an asymptote at x=0 and g(x)=log_b(x)-d is the translation function with an asymptote at x=0. This shows the translation of shifting down.
Figure 11

The domain is[latex]\,\left(0,\infty \right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=0.[/latex]

Try It

Sketch a graph of[latex]\,f\left(x\right)={\mathrm{log}}_{2}\left(x\right)+2\,[/latex]alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.
Show Solution
Graph of two functions. The parent function is y=log_2(x), with an asymptote at x=0 and labeled points at (1, 0), and (2, 1).The translation function f(x)=log_2(x)+2 has an asymptote at x=0 and labeled points at (0.25, 0) and (0.5, 1).
Figure 12

 

The domain is[latex]\,\left(0,\infty \right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=0.[/latex]

Graphing Stretches and Compressions of y = logb(x)

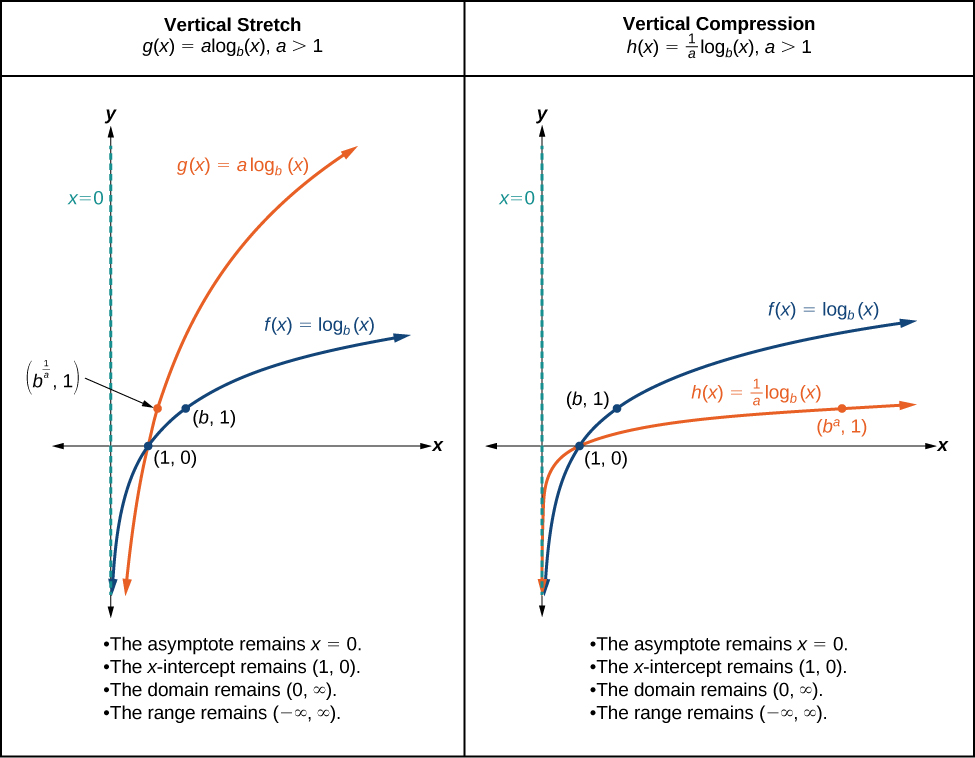
When the parent function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]is multiplied by a constant[latex]\,a>0,[/latex] the result is a vertical stretch or compression of the original graph. To visualize stretches and compressions, we set[latex]\,a>1\,[/latex]and observe the general graph of the parent function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]alongside the vertical stretch,[latex]\,g\left(x\right)=a{\mathrm{log}}_{b}\left(x\right)\,[/latex]and the vertical compression,[latex]\,h\left(x\right)=\frac{1}{a}{\mathrm{log}}_{b}\left(x\right).[/latex] (See Figure 13).

 

Graph of two functions. The parent function is f(x)=log_b(x), with an asymptote at x=0 and g(x)=alog_b(x) when a>1 is the translation function with an asymptote at x=0. The graph note the intersection of the two lines at (1, 0). This shows the translation of a vertical stretch.
Figure 13

Vertical Stretches and Compressions of the Parent Function y = logb(x)

For any constant[latex]\,a>1,[/latex] the function[latex]\,f\left(x\right)=a{\mathrm{log}}_{b}\left(x\right)[/latex]

  • stretches the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]vertically by a factor of[latex]\,a\,[/latex]if[latex]\,a>1.[/latex]
  • compresses the parent function y = logb (x) vertically by a factor of a if [latex]\,0 \lt a \lt 1[/latex].
  • has the vertical asymptote[latex]\,x=0.[/latex]
  • has the x-intercept[latex]\,\left(1,0\right).[/latex]
  • has domain[latex]\,\left(0,\infty \right).[/latex]
  • has range[latex]\,\left(-\infty ,\infty \right).[/latex]

How To

Given a logarithmic function with the form[latex]\,f\left(x\right)=a{\mathrm{log}}_{b}\left(x\right),[/latex][latex]a>0,[/latex] graph the translation.

  1. Identify the vertical stretch or compressions:
    • If[latex]\,|a|>1,[/latex] the graph of[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]is stretched by a factor of[latex]\,a\,[/latex]units.
    • If[latex]\,|a| \lt 1,[/latex] the graph of[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]is compressed by a factor of[latex]\,a\,[/latex]units.
  2. Draw the vertical asymptote[latex]\,x=0.[/latex]
  3. Identify three key points from the parent function. Find new coordinates for the shifted functions by multiplying the[latex]\,y\,[/latex]coordinates by[latex]\,a.[/latex]
  4. Label the three points.
  5. The domain is[latex]\,\left(0,\infty \right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=0.[/latex]

 

Graphing a Stretch or Compression of the Parent Function y = logb(x)

Sketch a graph of[latex]\,f\left(x\right)=2{\mathrm{log}}_{4}\left(x\right)\,[/latex]alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

Show Solution

Since the function is[latex]\,f\left(x\right)=2{\mathrm{log}}_{4}\left(x\right),[/latex]we will notice[latex]\,a=2.[/latex]

This means we will stretch the function[latex]\,f\left(x\right)={\mathrm{log}}_{4}\left(x\right)\,[/latex]by a factor of 2.

The vertical asymptote is[latex]\,x=0.[/latex]

Consider the three key points from the parent function,[latex]\,\left(\frac{1}{4},-1\right),[/latex][latex]\left(1,0\right),\,[/latex]and[latex]\,\left(4,1\right).[/latex]

The new coordinates are found by multiplying the[latex]\,y\,[/latex]coordinates by 2.

Label the points[latex]\,\left(\frac{1}{4},-2\right),[/latex][latex]\left(1,0\right)\,,[/latex] and[latex]\,\left(4,\text{2}\right).[/latex]

The domain is[latex]\,\left(0,\,\infty \right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),\,[/latex]and the vertical asymptote is[latex]\,x=0.\,[/latex] (See Figure 14).

 

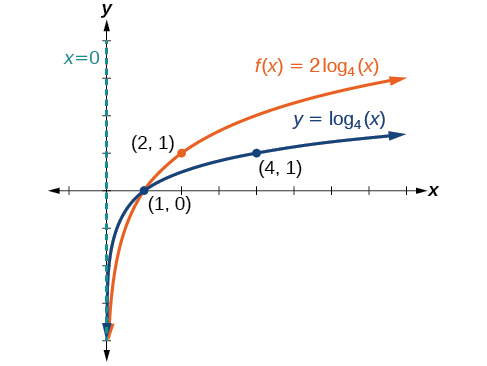
Graph of two functions. The parent function is y=log_4(x), with an asymptote at x=0 and labeled points at (1, 0), and (4, 1).The translation function f(x)=2log_4(x) has an asymptote at x=0 and labeled points at (1, 0) and (2, 1).
Figure 14

 

The domain is[latex]\,\left(0,\infty \right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=0.[/latex]

 

 

Try It

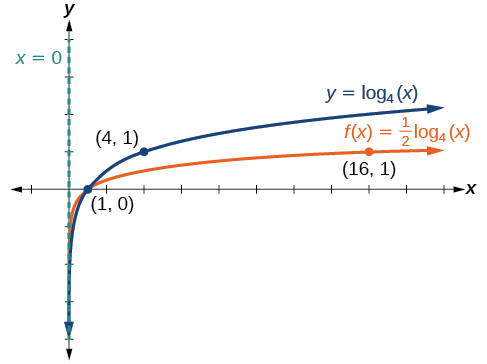
Sketch a graph of[latex]\,f\left(x\right)=\frac{1}{2}\,{\mathrm{log}}_{4}\left(x\right)\,[/latex]alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

Show Solution
Graph of two functions. The parent function is y=log_4(x), with an asymptote at x=0 and labeled points at (1, 0), and (4, 1).The translation function f(x)=(1/2)log_4(x) has an asymptote at x=0 and labeled points at (1, 0) and (16, 1).
Figure 15

 

The domain is[latex]\,\left(0,\infty \right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=0.[/latex]

Combining a Shift and a Stretch

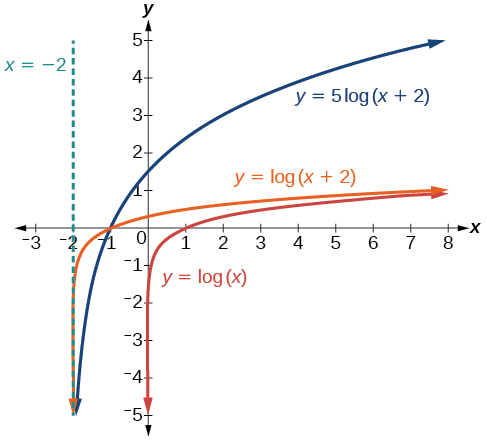
Sketch a graph of[latex]\,f\left(x\right)=5\mathrm{log}\left(x+2\right).\,[/latex]State the domain, range, and asymptote.

Show Solution

Remember: what happens inside parentheses happens first. First, we move the graph left 2 units, then stretch the function vertically by a factor of 5, as in Figure 16. The vertical asymptote will be shifted to[latex]\,x=-2.\,[/latex]The x-intercept will be[latex]\,\left(-1,0\right).\,[/latex]The domain will be[latex]\,\left(-2,\infty \right).\,[/latex]Two points will help give the shape of the graph:[latex]\,\left(-1,0\right)\,[/latex]and[latex]\,\left(8,5\right).\,[/latex]We chose[latex]\,x=8\,[/latex]as the x-coordinate of one point to graph because when[latex]\,x=8,\,[/latex][latex]\,x+2=10,\,[/latex]the base of the common logarithm.

 

Graph of three functions. The parent function is y=log(x), with an asymptote at x=0. The first translation function y=5log(x+2) has an asymptote at x=-2. The second translation function y=log(x+2) has an asymptote at x=-2.
Figure 16

 

The domain is[latex]\,\left(-2,\infty \right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=-2.[/latex]

Try It

Sketch a graph of the function[latex]\,f\left(x\right)=3\mathrm{log}\left(x-2\right)+1.\,[/latex]State the domain, range, and asymptote.

Show Solution
Graph of f(x)=3log(x-2)+1 with an asymptote at x=2.
Figure 17

 

The domain is[latex]\,\left(2,\infty \right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=2.[/latex]

Graphing Reflections of f(x) = logb(x)

When the parent function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]is multiplied by[latex]\,-1,[/latex]the result is a reflection about the x-axis. When the input is multiplied by[latex]\,-1,[/latex]the result is a reflection about the y-axis. To visualize reflections, we restrict[latex]\,b>1,\,[/latex]and observe the general graph of the parent function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]alongside the reflection about the x-axis,[latex]\,g\left(x\right)={\mathrm{-log}}_{b}\left(x\right)\,[/latex]and the reflection about the y-axis,[latex]\,h\left(x\right)={\mathrm{log}}_{b}\left(-x\right).[/latex]

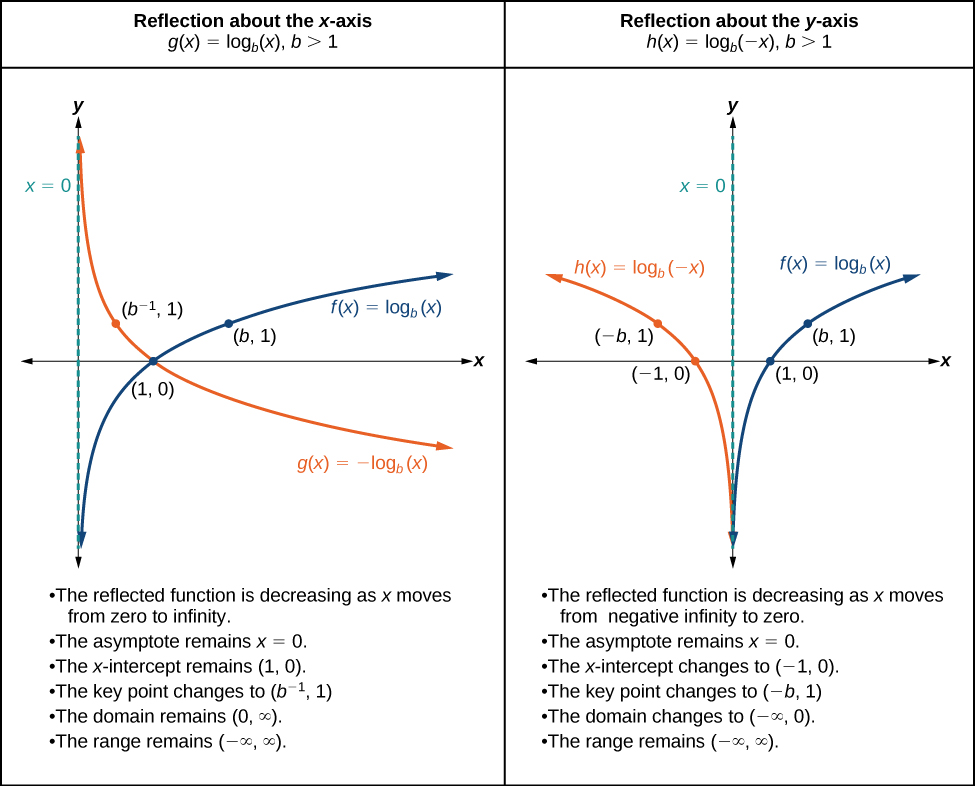
Graph of two functions. The parent function is f(x)=log_b(x), with an asymptote at x=0 and g(x)=-log_b(x) when b>1 is the translation function with an asymptote at x=0. The graph note the intersection of the two lines at (1, 0). This shows the translation of a reflection about the x-axis.
Figure 18

Reflections of the Parent Function y = logb(x)

The function[latex]\,f\left(x\right)={\mathrm{-log}}_{b}\left(x\right)[/latex]

  • reflects the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]about the x-axis.
  • has domain,[latex]\,\left(0,\infty \right),[/latex] range,[latex]\,\left(-\infty ,\infty \right),[/latex] and vertical asymptote,[latex]\,x=0,[/latex] which are unchanged from the parent function.

The function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(-x\right)[/latex]

  • reflects the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]about the y-axis.
  • has domain[latex]\,\left(-\infty ,0\right).[/latex]
  • has range,[latex]\,\left(-\infty ,\infty \right),[/latex] and vertical asymptote,[latex]\,x=0,[/latex] which are unchanged from the parent function.

How To

Given a logarithmic function with the parent function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right),[/latex] graph a translation.

[latex]\text{If }f\left(x\right)=-{\mathrm{log}}_{b}\left(x\right)[/latex] [latex]\text{If }f\left(x\right)={\mathrm{log}}_{b}\left(-x\right)[/latex]
  1. Draw the vertical asymptote,[latex]\,x=0.[/latex]
  1. Draw the vertical asymptote,[latex]\,x=0.[/latex]
  1. Plot the x-intercept,[latex]\,\left(1,0\right).[/latex]
  1. Plot the x-intercept,[latex]\,\left(1,0\right).[/latex]
  1. Reflect the graph of the parent function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]about the x-axis.
  1. Reflect the graph of the parent function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]about the y-axis.
  1. Draw a smooth curve through the points.
  1. Draw a smooth curve through the points.
  1. State the domain,[latex]\,\left(0,\infty \right),[/latex] the range,[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote[latex]\,x=0.[/latex]
    1. State the domain,[latex]\,\left(-\infty ,0\right),[/latex] the range,[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote[latex]\,x=0.[/latex]

Table 3

 

Graphing a Reflection of a Logarithmic Function

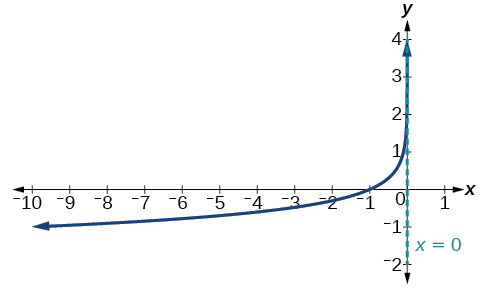
Sketch a graph of[latex]\,f\left(x\right)=\mathrm{log}\left(-x\right)\,[/latex]alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

Show Solution

Before graphing[latex]\,f\left(x\right)=\mathrm{log}\left(-x\right),[/latex]identify the behavior and key points for the graph.

  • Since[latex]\,b=10\,[/latex]is greater than one, we know that the parent function is increasing. Since the input value is multiplied by[latex]\,-1,[/latex][latex]f\,[/latex]is a reflection of the parent graph about the y-axis. Thus,[latex]\,f\left(x\right)=\mathrm{log}\left(-x\right)\,[/latex]will be decreasing as[latex]\,x\,[/latex]moves from negative infinity to zero, and the right tail of the graph will approach the vertical asymptote[latex]\,x=0.\,[/latex]
  • The x-intercept is[latex]\,\left(-1,0\right).[/latex]
  • We draw and label the asymptote, plot and label the points, and draw a smooth curve through the points.
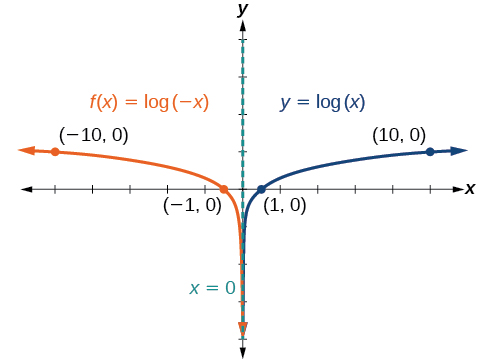
Graph of two functions. The parent function is y=log(x), with an asymptote at x=0 and labeled points at (1, 0), and (10, 1).The translation function f(x)=log(-x) has an asymptote at x=0 and labeled points at (-1, 0) and (-10, 1).
Figure 19

The domain is[latex]\,\left(-\infty ,0\right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=0.[/latex]

Try It

Graph[latex]\,f\left(x\right)=-\mathrm{log}\left(-x\right).\,[/latex]State the domain, range, and asymptote.

Show Solution

 

Graph of f(x)=-log(-x) with an asymptote at x=0.
Figure 20

 

The domain is[latex]\,\left(-\infty ,0\right),[/latex] the range is[latex]\,\left(-\infty ,\infty \right),[/latex] and the vertical asymptote is[latex]\,x=0.[/latex]

How To

Given a logarithmic equation, use a graphing calculator to approximate solutions.

  1. Press [Y=]. Enter the given logarithm equation or equations as Y1= and, if needed, Y2=.
  2. Press [GRAPH] to observe the graphs of the curves and use [WINDOW] to find an appropriate view of the graphs, including their point(s) of intersection.
  3. To find the value of[latex]\,x,[/latex] we compute the point of intersection. Press [2ND] then [CALC]. Select “intersect” and press [ENTER] three times. The point of intersection gives the value of[latex]\,x[/latex] for the point(s) of intersection.

Approximating the Solution of a Logarithmic Equation

Solve[latex]\,4\mathrm{ln}\left(x\right)+1=-2\mathrm{ln}\left(x-1\right)\,[/latex]graphically. Round to the nearest thousandth.

Show Solution

Press [Y=] and enter[latex]\,4\mathrm{ln}\left(x\right)+1\,[/latex]next to Y1=. Then enter[latex]\,-2\mathrm{ln}\left(x-1\right)\,[/latex]next to Y2=. For a window, use the values 0 to 5 for[latex]\,x\,[/latex]and –10 to 10 for[latex]\,y.\,[/latex]Press [GRAPH]. The graphs should intersect somewhere a little to the right of[latex]\,x=1.[/latex]

For a better approximation, press [2ND] then [CALC]. Select [5: intersect] and press [ENTER] three times. The x-coordinate of the point of intersection is displayed as 1.3385297. (Your answer may be different if you use a different window or use a different value for Guess?) So, to the nearest thousandth,[latex]\,x\approx 1.339.[/latex]

Try It

Solve[latex]\,5\mathrm{log}\left(x+2\right)=4-\mathrm{log}\left(x\right)\,[/latex]graphically. Round to the nearest thousandth.

Show Solution

[latex]x\approx 3.049[/latex]

Summarizing Translations of the Logarithmic Function

Now that we have worked with each type of translation for the logarithmic function, we can summarize each in Table 2 to arrive at the general equation for translating exponential functions.

 
Translations of the Parent Function[latex]\,y={\mathrm{log}}_{b}\left(x\right)[/latex]
Translation Form
Shift
  • Horizontally[latex]\,c\,[/latex]units to the left
  • Vertically[latex]\,d\,[/latex]units up
 [latex]y={\mathrm{log}}_{b}\left(x+c\right)+d[/latex]
Stretch and Compress
  • Stretch if[latex]\,|a|>1[/latex]
  • Compression if[latex]|a|\lt1[/latex]
 [latex]y=a{\mathrm{log}}_{b}\left(x\right)[/latex]
Reflect about the x-axis [latex]y=-{\mathrm{log}}_{b}\left(x\right)[/latex]
Reflect about the y-axis [latex]y={\mathrm{log}}_{b}\left(-x\right)[/latex]
General equation for all translations [latex]y=a{\mathrm{log}}_{b}\left(x+c\right)+d[/latex]
Table 4

Translations of Logarithmic Functions

All translations of the parent logarithmic function,[latex]\,y={\mathrm{log}}_{b}\left(x\right),[/latex] have the form

[latex]f\left(x\right)=a{\mathrm{log}}_{b}\left(x+c\right)+d[/latex]

where the parent function,[latex]\,y={\mathrm{log}}_{b}\left(x\right),b>1,[/latex]is

  • shifted vertically up[latex]\,d\,[/latex]units.
  • shifted horizontally to the left[latex]\,c\,[/latex]units.
  • stretched vertically by a factor of [latex]\,|a|[/latex] if [latex]\,|a| > 0[/latex].
  • compressed vertically by a factor of[latex]\,|a|\,[/latex]if[latex]\, 0 \lt |a| \lt 1[/latex].
  • reflected about the x-axis when [latex]\,a \lt 0[/latex].

For[latex]\,f\left(x\right)=\mathrm{log}\left(-x\right),[/latex] the graph of the parent function is reflected about the y-axis.

Finding the Vertical Asymptote of a Logarithm Graph

What is the vertical asymptote of[latex]\,f\left(x\right)=-2{\mathrm{log}}_{3}\left(x+4\right)+5?[/latex]

Show Solution

The vertical asymptote is at[latex]\,x=-4.[/latex]

Analysis

The coefficient, the base, and the upward translation do not affect the asymptote. The shift of the curve 4 units to the left shifts the vertical asymptote to[latex]\,x=-4.[/latex]

Try It

What is the vertical asymptote of[latex]\,f\left(x\right)=3+\mathrm{ln}\left(x-1\right)?[/latex]

Show Solution

[latex]x=1[/latex]

Finding the Equation from a Graph

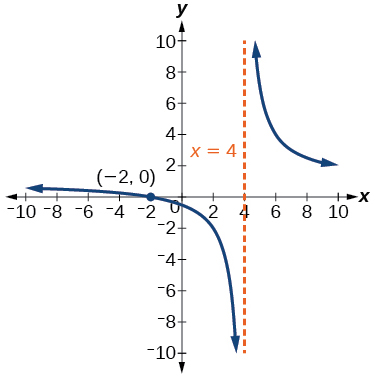
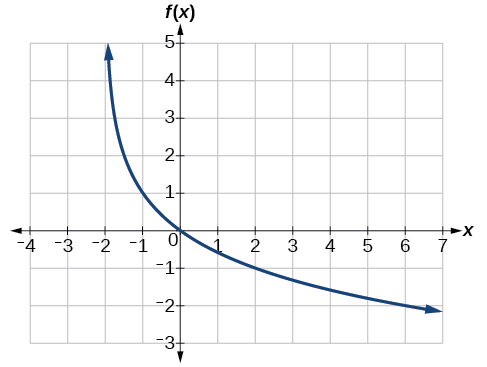
Find a possible equation for the common logarithmic function graphed in Figure 21.

 

Graph of a logarithmic function with a vertical asymptote at x=-2, has been vertically reflected, and passes through the points (-1, 1) and (2, -1).
Figure 21
Show Solution

This graph has a vertical asymptote at[latex]\,x=–2\,[/latex]and has been vertically reflected. We do not know yet the vertical shift or the vertical stretch. We know so far that the equation will have the following form:

[latex]f\left(x\right)=-a\mathrm{log}\left(x+2\right)+k[/latex]

It appears the graph passes through the points[latex]\,\left(–1,1\right)\,[/latex]and[latex]\,\left(2,–1\right).\,[/latex]Substituting[latex]\,\left(–1,1\right),[/latex]

[latex]\begin{array}{ll}1=-a\mathrm{log}\left(-1+2\right)+k\,\,\,\,\,\,\,\,\,\,\,\,\hfill & \text{Substitute }\left(-1,1\right).\hfill \\ 1=-a\mathrm{log}\left(1\right)+k\hfill & \text{Arithmetic}.\hfill \\ 1=k\hfill & \text{log(1)}=0.\hfill \end{array}[/latex]

Next, substituting in[latex]\,\left(2,–1\right)[/latex],

[latex]\begin{array}{lll}-1=-a\mathrm{log}\left(2+2\right)+1\hfill & \hfill & \text{Plug in }\left(2,-1\right).\hfill \\ -2=-a\mathrm{log}\left(4\right)\hfill & \hfill & \text{Arithmetic}.\hfill \\ \text{ }a=\frac{2}{\mathrm{log}\left(4\right)}\hfill & \hfill & \text{Solve for }a.\hfill \end{array}[/latex]

This gives us the equation[latex]\,f\left(x\right)=–\frac{2}{\mathrm{log}\left(4\right)}\mathrm{log}\left(x+2\right)+1.[/latex]

Analysis

We can verify this answer by comparing the function values in Table 5 with the points on the graph in Figure 21.

[latex]x[/latex] −1 0 1 2 3
[latex]f\left(x\right)[/latex] 1 0 −0.58496 −1 −1.3219
[latex]x[/latex] 4 5 6 7 8
[latex]f\left(x\right)[/latex] −1.5850 −1.8074 −2 −2.1699 −2.3219

Table 5

Try It

Give the equation of the natural logarithm graphed in Figure 22.

Graph of a logarithmic function with a vertical asymptote at x=-3, has been vertically stretched by 2, and passes through the points (-1, -1).
Figure 22
Show Solution

[latex]f\left(x\right)=2\mathrm{ln}\left(x+3\right)-1[/latex]

Is it possible to tell the domain and range and describe the end behavior of a function just by looking at the graph?

Yes, if we know the function is a general logarithmic function. For example, look at the graph in Figure 22. The graph approaches[latex]\,x=-3\,[/latex](or thereabouts) more and more closely, so[latex]\,x=-3\,[/latex]is, or is very close to, the vertical asymptote. It approaches from the right, so the domain is all points to the right,[latex]\,\left\{x\,|\,x>-3\right\}.\,[/latex]The range, as with all general logarithmic functions, is all real numbers. And we can see the end behavior because the graph goes down as it goes left and up as it goes right. The end behavior is that as[latex]\,x\to -{3}^{+},f\left(x\right)\to -\infty \,[/latex]and as[latex]\,x\to \infty ,f\left(x\right)\to \infty .[/latex]

 

Key Equations

General Form for the Translation of the Parent Logarithmic Function[latex]\text{ }f\left(x\right)= {\mathrm{log}}_{b}\left(x\right)[/latex]

[latex]f\left(x\right)=a{\mathrm{log}}_{b}\left(x+c\right)+d[/latex]

 

Key Concepts

  • To find the domain of a logarithmic function, set up an inequality showing the argument greater than zero, and solve for x.
    • The graph of the parent function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)\,[/latex]has an x-intercept at[latex]\,\left(1,0\right),[/latex] domain[latex]\,\left(0,\infty \right),[/latex] range[latex]\,\left(-\infty ,\infty \right),[/latex] vertical asymptote[latex]\,x=0,[/latex]and
    • if [latex]\,b > 1[/latex], the function is increasing.
    • if [latex]\,0 \lt b \lt 1[/latex], the function is decreasing.
    • left[latex]\,c\,[/latex]units if[latex]\,c>0.[/latex]
    • right[latex]\,c\,[/latex]units if [latex]\, c \lt 0[/latex] . The equation[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x+c\right)\,[/latex]shifts the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]horizontally
    • up[latex]\,d\,[/latex]units if[latex]\,d>0.[/latex]
    • down[latex]\,d\,[/latex]units if[latex]\,d \lt 0.[/latex]The equation[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right)+d\,[/latex]shifts the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]vertically
    • stretches the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]vertically by a factor of[latex]\,a\,[/latex]if[latex]\,|a|>1.[/latex]
    • compresses the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]vertically by a factor of[latex]\,a\,[/latex]if[latex]\,|a|1.[/latex] For any constant[latex]\,a>0,[/latex] the equation[latex]\,f\left(x\right)=a{\mathrm{log}}_{b}\left(x\right)[/latex]
    • The equation[latex]\,f\left(x\right)=-{\mathrm{log}}_{b}\left(x\right)\,[/latex]represents a reflection of the parent function about the x-axis.
    • The equation[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(-x\right)\,[/latex]represents a reflection of the parent function about the y-axis. When the parent function[latex]\,y={\mathrm{log}}_{b}\left(x\right)\,[/latex]is multiplied by[latex]\,-1,[/latex] the result is a reflection about the x-axis. When the input is multiplied by[latex]\,-1,[/latex] the result is a reflection about the y-axis.
    • A graphing calculator may be used to approximate solutions to some logarithmic equations.
  • All translations of the logarithmic function can be summarized by the general equation.
  • Given an equation with the general form[latex]\,f\left(x\right)=a{\mathrm{log}}_{b}\left(x+c\right)+d,[/latex]we can identify the vertical asymptote[latex]\,x=-c\,[/latex]for the transformation.
  • Using the general equation[latex]\,f\left(x\right)=a{\mathrm{log}}_{b}\left(x+c\right)+d,[/latex]we can write the equation of a logarithmic function given its graph.

Section Exercises

Verbal

  1. The inverse of every logarithmic function is an exponential function and vice-versa. What does this tell us about the relationship between the coordinates of the points on the graphs of each?
Show Solution

Since the functions are inverses, their graphs are mirror images about the line[latex]\,y=x.\,[/latex]So for every point[latex]\,\left(a,b\right)\,[/latex]on the graph of a logarithmic function, there is a corresponding point[latex]\,\left(b,a\right)\,[/latex]on the graph of its inverse exponential function.

  1. What type(s) of translation(s), if any, affect the range of a logarithmic function?
  1. What type(s) of translation(s), if any, affect the domain of a logarithmic function?
Show Solution

Shifting the function right or left and reflecting the function about the y-axis will affect its domain.

  1. Consider the general logarithmic function[latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x\right).\,[/latex]Why can’t[latex]\,x\,[/latex]be zero?
  1. Does the graph of a general logarithmic function have a horizontal asymptote? Explain.
Show Solution

No. A horizontal asymptote would suggest a limit on the range, and the range of any logarithmic function in general form is all real numbers.

Algebraic

For the following exercises, state the domain and range of the function.

  1. [latex]f\left(x\right)={\mathrm{log}}_{3}\left(x+4\right)[/latex]
  1. [latex]h\left(x\right)=\mathrm{ln}\left(\frac{1}{2}-x\right)[/latex]
Show Solution

Domain:[latex]\,\left(-\infty ,\frac{1}{2}\right);\,[/latex]Range:[latex]\,\left(-\infty ,\infty \right)[/latex]

  1. [latex]g\left(x\right)={\mathrm{log}}_{5}\left(2x+9\right)-2[/latex]
  1. [latex]h\left(x\right)=\mathrm{ln}\left(4x+17\right)-5[/latex]
Show Solution

Domain:[latex]\,\left(-\frac{17}{4},\infty \right);\,[/latex]Range:[latex]\,\left(-\infty ,\infty \right)[/latex]

  1. [latex]f\left(x\right)={\mathrm{log}}_{2}\left(12-3x\right)-3[/latex]

For the following exercises, state the domain and the vertical asymptote of the function.

  1. [latex]\,f\left(x\right)={\mathrm{log}}_{b}\left(x-5\right)[/latex]
Show Solution

Domain:[latex]\,\left(5,\infty \right);\,[/latex]Vertical asymptote:[latex]\,x=5[/latex]

  1. [latex]\,g\left(x\right)=\mathrm{ln}\left(3-x\right)[/latex]
  1. [latex]\,f\left(x\right)=\mathrm{log}\left(3x+1\right)[/latex]
Show Solution

Domain:[latex]\,\left(-\frac{1}{3},\infty \right);\,[/latex]Vertical asymptote:[latex]\,x=-\frac{1}{3}[/latex]

  1. [latex]\,f\left(x\right)=3\mathrm{log}\left(-x\right)+2[/latex]
  1. [latex]\,g\left(x\right)=-\mathrm{ln}\left(3x+9\right)-7[/latex]
Show Solution

Domain:[latex]\,\left(-3,\infty \right);\,[/latex]Vertical asymptote:[latex]\,x=-3[/latex]

For the following exercises, state the domain, vertical asymptote, and end behavior of the function.

  1. [latex]f\left(x\right)=\mathrm{ln}\left(2-x\right)[/latex]
  1. [latex]f\left(x\right)=\mathrm{log}\left(x-\frac{3}{7}\right)[/latex]
Show Solution

Domain: [latex]\left(\frac{3}{7},\infty \right)[/latex];

  1. [latex]h\left(x\right)=-\mathrm{log}\left(3x-4\right)+3[/latex]
  1. [latex]g\left(x\right)=\mathrm{ln}\left(2x+6\right)-5[/latex]
Show Solution

Domain: [latex]\left(-3,\infty \right)[/latex]; Vertical asymptote: [latex]x=-3[/latex];

  1. [latex]f\left(x\right)={\mathrm{log}}_{3}\left(15-5x\right)+6[/latex]

For the following exercises, state the domain, range, and x– and y-intercepts, if they exist. If they do not exist, write DNE.

  1. [latex]h\left(x\right)={\mathrm{log}}_{4}\left(x-1\right)+1[/latex]
Show Solution

Domain:[latex]\,\left(1,\infty \right);\,[/latex]Range:[latex]\,\left(-\infty ,\infty \right);\,[/latex]Vertical asymptote:[latex]\,x=1;\,[/latex]x-intercept:[latex]\,\left(\frac{5}{4},0\right);\,[/latex]y-intercept: DNE

  1. [latex]f\left(x\right)=\mathrm{log}\left(5x+10\right)+3[/latex]
  1. [latex]g\left(x\right)=\mathrm{ln}\left(-x\right)-2[/latex]
Show Solution

Domain:[latex]\,\left(-\infty ,0\right);\,[/latex]Range:[latex]\,\left(-\infty ,\infty \right);\,[/latex]Vertical asymptote:[latex]\,x=0;\,[/latex]x-intercept:[latex]\,\left(-{e}^{2},0\right);\,[/latex]y-intercept: DNE

  1. [latex]f\left(x\right)={\mathrm{log}}_{2}\left(x+2\right)-5[/latex]
  1. [latex]h\left(x\right)=3\mathrm{ln}\left(x\right)-9[/latex]
Show Solution

Domain:[latex]\,\left(0,\infty \right);\,[/latex]Range:[latex]\,\left(-\infty ,\infty \right);\,[/latex] Vertical asymptote: [latex]\,x=0;\,[/latex]x-intercept:[latex]\,\left({e}^{3},0\right);\,[/latex]y-intercept: DNE

Graphical

For the following exercises, match each function in Figure 23 with the letter corresponding to its graph.

 

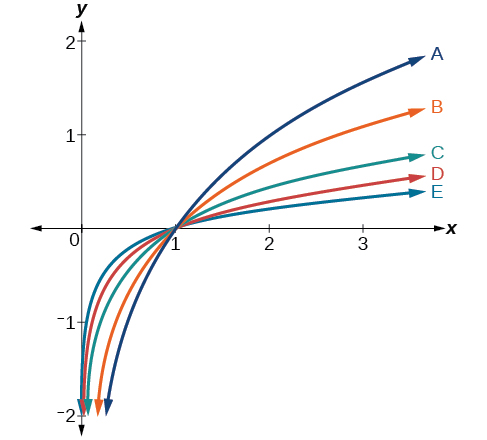
Graph of five logarithmic functions.
Figure 23
  1. [latex]d\left(x\right)=\mathrm{log}\left(x\right)[/latex]
  1. [latex]f\left(x\right)=\mathrm{ln}\left(x\right)[/latex]
Show Solution

B

  1. [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex]
  1. [latex]h\left(x\right)={\mathrm{log}}_{5}\left(x\right)[/latex]
Show Solution

C

  1. [latex]j\left(x\right)={\mathrm{log}}_{25}\left(x\right)[/latex]

For the following exercises, match each function in Figure 24 with the letter corresponding to its graph.

 

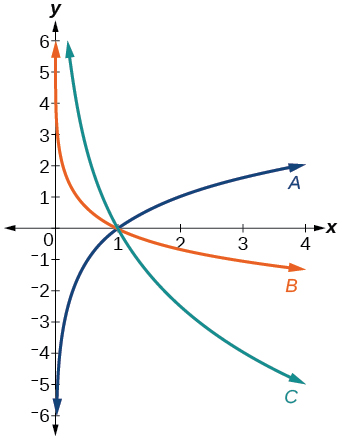
Graph of three logarithmic functions.
Figure 24
  1. [latex]f\left(x\right)={\mathrm{log}}_{\frac{1}{3}}\left(x\right)[/latex]
Show Solution

B

  1. [latex]g\left(x\right)={\mathrm{log}}_{2}\left(x\right)[/latex]
  1. [latex]h\left(x\right)={\mathrm{log}}_{\frac{3}{4}}\left(x\right)[/latex]
Show Solution

C

For the following exercises, sketch the graphs of each pair of functions on the same axis.

  1. [latex]f\left(x\right)=\mathrm{log}\left(x\right)\,[/latex]and[latex]\,g\left(x\right)={10}^{x}[/latex]
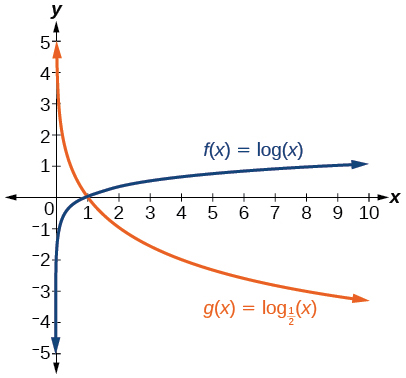
  1. [latex]f\left(x\right)=\mathrm{log}\left(x\right)\,[/latex]and[latex]\,g\left(x\right)={\mathrm{log}}_{\frac{1}{2}}\left(x\right)[/latex]
Show Solution

Graph of two functions, g(x) = log_(1/2)(x) in orange and f(x)=log(x) in blue.

 

  1. [latex]f\left(x\right)={\mathrm{log}}_{4}\left(x\right)\,[/latex]and[latex]\,g\left(x\right)=\mathrm{ln}\left(x\right)[/latex]
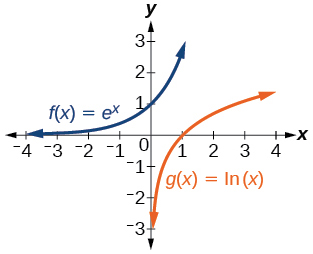
  1. [latex]f\left(x\right)={e}^{x}\,[/latex]and[latex]\,g\left(x\right)=\mathrm{ln}\left(x\right)[/latex]
Show Solution

Graph of two functions, g(x) = ln(1/2)(x) in orange and f(x)=e^(x) in blue.

 

For the following exercises, match each function in Figure 27 with the letter corresponding to its graph.

 

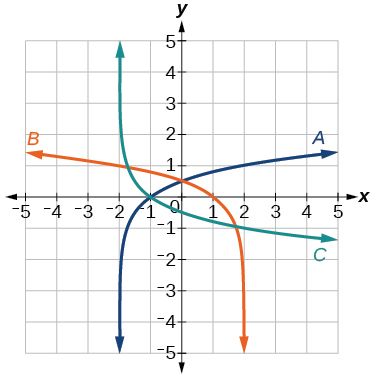
Graph of three logarithmic functions.
Figure 27
  1. [latex]f\left(x\right)={\mathrm{log}}_{4}\left(-x+2\right)[/latex]
  1. [latex]g\left(x\right)=-{\mathrm{log}}_{4}\left(x+2\right)[/latex]
Show Solution

C

  1. [latex]h\left(x\right)={\mathrm{log}}_{4}\left(x+2\right)[/latex]

For the following exercises, sketch the graph of the indicated function.

  1. [latex]\,f\left(x\right)={\mathrm{log}}_{2}\left(x+2\right)[/latex]
Show Solution

The graph y=log_4(x) has been vertically stretched by 3, and shifted to the left by 2.

 

  1. [latex]\,f\left(x\right)=2\mathrm{log}\left(x\right)[/latex]
  1. [latex]\,f\left(x\right)=\mathrm{ln}\left(-x\right)[/latex]
Show Solution

Graph f(x) = ln (-x)

 

  1. [latex]g\left(x\right)=\mathrm{log}\left(4x+16\right)+4[/latex]
  1. [latex]g\left(x\right)=\mathrm{log}\left(6-3x\right)+1[/latex]
Show Solution

Graph of f(x)=2^(x) with the following translations: a reflection about the x-axis, and a shift up by 3.

  1. [latex]h\left(x\right)=-\frac{1}{2}\mathrm{ln}\left(x+1\right)-3[/latex]

For the following exercises, write a logarithmic equation corresponding to the graph shown.

  1. Use[latex]\,y={\mathrm{log}}_{2}\left(x\right)\,[/latex]as the parent function.

The graph y=log_2(x) has been reflected over the y-axis and shifted to the right by 1.

Show Solution

[latex]\,f\left(x\right)={\mathrm{log}}_{2}\left(-\left(x-1\right)\right)[/latex]

  1. Use[latex]\,f\left(x\right)={\mathrm{log}}_{3}\left(x\right)\,[/latex]as the parent function.

The graph y=log_3(x) has been reflected over the x-axis, vertically stretched by 3, and shifted to the left by 4.

  1. Use[latex]\,f\left(x\right)={\mathrm{log}}_{4}\left(x\right)\,[/latex]as the parent function.

The graph y=log_4(x) has been vertically stretched by 3, and shifted to the left by 2.

Show Solution

[latex]f\left(x\right)=3{\mathrm{log}}_{4}\left(x+2\right)[/latex]

  1. Use[latex]\,f\left(x\right)={\mathrm{log}}_{5}\left(x\right)\,[/latex]as the parent function.

The graph y=log_3(x) has been reflected over the x-axis and y-axis, vertically stretched by 2, and shifted to the right by 5.

Technology

For the following exercises, use a graphing calculator to find approximate solutions to each equation.

  1. [latex]\mathrm{log}\left(x-1\right)+2=\mathrm{ln}\left(x-1\right)+2[/latex]
Show Solution

[latex]x=2[/latex]

  1. [latex]\mathrm{log}\left(2x-3\right)+2=-\mathrm{log}\left(2x-3\right)+5[/latex]
  1. [latex]\mathrm{ln}\left(x-2\right)=-\mathrm{ln}\left(x+1\right)[/latex]
Show Solution

[latex]x\approx \text{2}\text{.303}[/latex]

  1. [latex]2\mathrm{ln}\left(5x+1\right)=\frac{1}{2}\mathrm{ln}\left(-5x\right)+1[/latex]
  1. [latex]\frac{1}{3}\mathrm{log}\left(1-x\right)=\mathrm{log}\left(x+1\right)+\frac{1}{3}[/latex]
Show Solution

[latex]x\approx -0.472[/latex]

Extensions

  1. Let[latex]\,b\,[/latex]be any positive real number such that[latex]\,b\ne 1.\,[/latex]What must[latex]\,{\mathrm{log}}_{b}1\,[/latex]be equal to? Verify the result.
  1. Explore and discuss the graphs of[latex]\,f\left(x\right)={\mathrm{log}}_{\frac{1}{2}}\left(x\right)\,[/latex]and[latex]\,g\left(x\right)=-{\mathrm{log}}_{2}\left(x\right).\,[/latex]Make a conjecture based on the result.
Show Solution

The graphs of[latex]\,f\left(x\right)={\mathrm{log}}_{\frac{1}{2}}\left(x\right)\,[/latex]and[latex]\,g\left(x\right)=-{\mathrm{log}}_{2}\left(x\right)\,[/latex]appear to be the same; Conjecture: for any positive base[latex]\,b\ne 1,[/latex][latex]\,{\mathrm{log}}_{b}\left(x\right)=-{\mathrm{log}}_{\frac{1}{b}}\left(x\right).[/latex]

  1. Prove the conjecture made in the previous exercise.
  1. What is the domain of the function[latex]\,f\left(x\right)=\mathrm{ln}\left(\frac{x+2}{x-4}\right)?\,[/latex]Discuss the result.
Show Solution

Recall that the argument of a logarithmic function must be positive, so we determine where[latex]\,\frac{x+2}{x-4}>0\,[/latex]. From the graph of the function[latex]\,f\left(x\right)=\frac{x+2}{x-4},[/latex] note that the graph lies above the x-axis on the interval[latex]\,\left(-\infty ,-2\right)\,[/latex]and again to the right of the vertical asymptote—that is, [latex]\,\left(4,\infty \right).\,[/latex]Therefore, the domain is[latex]\,\left(-\infty ,-2\right)\cup \left(4,\infty \right).[/latex]

Graph f(x) = (x+2)/(x-4)

  1. Use properties of exponents to find the x-intercepts of the function[latex]\,f\left(x\right)=\mathrm{log}\left({x}^{2}+4x+4\right)\,[/latex]algebraically. Show the steps for solving, and then verify the result by graphing the function.

Media Attributions

License

Icon for the Creative Commons Attribution 4.0 International License

College Algebra Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book