Chapter 2 Equations and Inequalities

Chapter 2 Practice Test

Chapter Practice Test

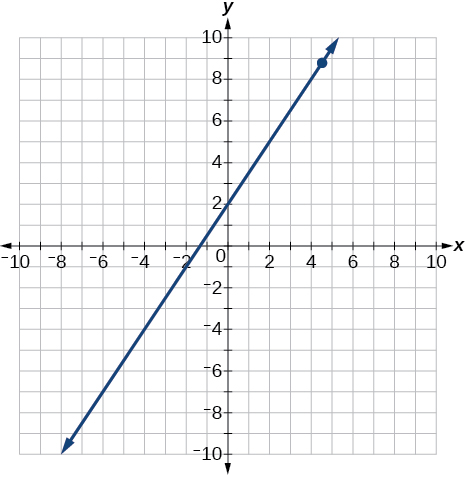
  1. Graph the following:[latex]\,2y=3x+4.[/latex]
Show Solution

[latex]y=\frac{3}{2}x+2[/latex]

 
x y
0 2
2 5
4 8

A coordinate plane with the x and y axes ranging from -10 to 10. The line going through the points (0,2); (2,5); and (4,8) is graphed.

 

  1. Find the x- and y-intercepts for the following: [latex]2x-5y=6[/latex]
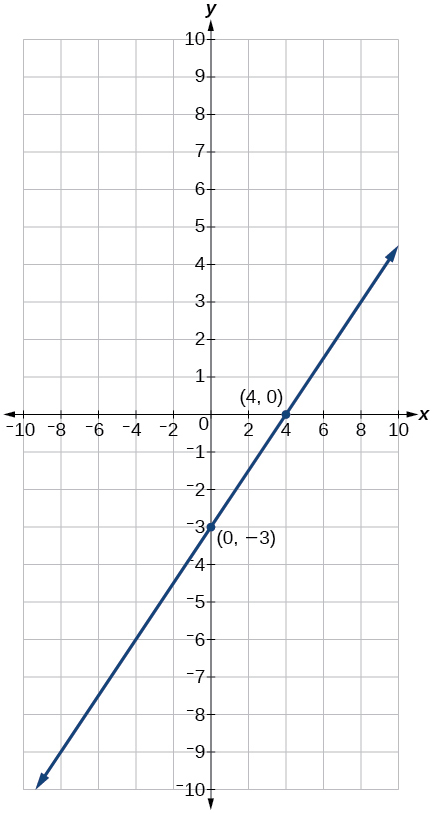
  1. Find the x- and y-intercepts of this equation, and sketch the graph of the line using just the intercepts plotted: [latex]3x-4y=12[/latex]
Show Solution

[latex]\left(0,-3\right)[/latex][latex]\left(4,0\right)[/latex]

A coordinate plane with the x and y axes ranging from -10 to 10. The points (4,0) and (0,-3) are plotted with a line running through them.

 

  1. Find the exact distance between[latex]\,\left(5,-3\right)\,[/latex]and[latex]\,\left(-2,8\right).\,[/latex]Find the coordinates of the midpoint of the line segment joining the two points.
  1. Write the interval notation for the set of numbers represented by[latex]\,\left\{x|x\le 9\right\}.[/latex]
Show Solution

[latex]\left(-\infty ,9\right][/latex]

  1. Solve for x:[latex]\,5x+8=3x-10.[/latex]
  1. Solve for x:[latex]\,3\left(2x-5\right)-3\left(x-7\right)=2x-9.[/latex]
Show Solution

[latex]x=-15[/latex]

  1. Solve for x:[latex]\,\frac{x}{2}+1=\frac{4}{x}[/latex]
  1. Solve for x:[latex]\,\frac{5}{x+4}=4+\frac{3}{x-2}.[/latex]
Show Solution

[latex]x\ne -4,2;  \  [/latex][latex]x=\frac{-5}{2},1[/latex]

  1. The perimeter of a triangle is 30 in. The longest side is 2 less than 3 times the shortest side and the other side is 2 more than twice the shortest side. Find the length of each side.
  1. Solve for x. Write the answer in the simplest radical form:  [latex]\frac{{x}^{2}}{3}-x=\frac{-1}{2}[/latex]
Show Solution

[latex]x=\frac{3±\sqrt{3}}{2}[/latex]

  1. Solve:[latex]\,3x-8\le 4.[/latex]
  1. Solve:[latex]\,|2x+3|<5.[/latex]
Show Solution

[latex]\left(-4,1\right)[/latex]

  1. Solve:[latex]\,|3x-2|\ge 4.[/latex]
  1. Add these complex numbers:[latex]\,\left(3-2i\right)+\left(4-i\right).[/latex]
  1. Simplify:[latex]\,\sqrt{-4}+3\sqrt{-16}.[/latex]
Show Solution

[latex]14i[/latex]

  1. Multiply:[latex]\,5i\left(5-3i\right).[/latex]
  1. Divide:[latex]\,\frac{4-i}{2+3i}.[/latex]
Show Solution

[latex]\frac{5}{13}-\frac{14}{13}i[/latex]

  1. Solve this quadratic equation and write the two complex roots in[latex]\,a+bi\,[/latex]form:[latex]\,{x}^{2}-4x+7=0.[/latex]
  1. Solve:[latex]\,{\left(3x-1\right)}^{2}-1=24.[/latex]
Show Solution

[latex]x=2,\frac{-4}{3}[/latex]

  1. Solve:[latex]\,{x}^{2}-6x=13.[/latex]
  1. Solve:[latex]\,4{x}^{2}-4x-1=0[/latex]
Show Solution

[latex]x=\frac{1}{2}±\frac{\sqrt{2}}{2}[/latex]

  1. Solve: [latex]\sqrt{x-7}=x-7[/latex]
  1. Solve:[latex]\,2+\sqrt{12-2x}=x[/latex]
Show Solution

[latex]4[/latex]

  1. Solve:[latex]\,{\left(x-1\right)}^{\frac{2}{3}}=9[/latex]

For the following exercises, find the real solutions of each equation by factoring.

  1. [latex]2{x}^{3}-{x}^{2}-8x+4=0[/latex]
Show Solution

[latex]x=\frac{1}{2},2,-2[/latex]

  1. [latex]{\left(x+5\right)}^{2}-3\left(x+5\right)-4=0[/latex]

Media Attributions

License

Icon for the Creative Commons Attribution 4.0 International License

College Algebra Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book