Chapter 2 Equations and Inequalities

Chapter 2 Review Exercises

Chapter Review Exercises

The Rectangular Coordinate Systems and Graphs

For the following exercises, find the x-intercept and the y-intercept without graphing.

  1. [latex]4x-3y=12[/latex]
Show Solution

x-intercept:[latex]\,\left(3,0\right);[/latex] y-intercept:[latex]\,\left(0,-4\right)[/latex]

  1. [latex]2y-4=3x[/latex]

For the following exercises, solve for y in terms of x, putting the equation in slope–intercept form.

  1. [latex]5x=3y-12[/latex]
Show Solution

[latex]y=\frac{5}{3}x+4[/latex]

  1. [latex]2x-5y=7[/latex]

For the following exercises, find the distance between the two points.

  1. [latex]\left(-2,5\right)\left(4,-1\right)[/latex]
Show Solution

[latex]\sqrt{72}=6\sqrt{2}[/latex]

  1. [latex]\left(-12,-3\right)\left(-1,5\right)[/latex]
  1. Find the distance between the two points[latex]\,\left(-71,432\right)\,[/latex]and[latex]\,\text{(511,218)}\,[/latex]using your calculator, and round your answer to the nearest thousandth.
Show Solution

[latex]620.097[/latex]

For the following exercises, find the coordinates of the midpoint of the line segment that joins the two given points.

  1. [latex]\left(-1,5\right)\text{ and }\left(4,6\right)[/latex]
  1. [latex]\left(-13,5\right)\text{ and }\left(17,18\right)[/latex]
Show Solution

midpoint is[latex]\,\left(2,\frac{23}{2}\right)[/latex]

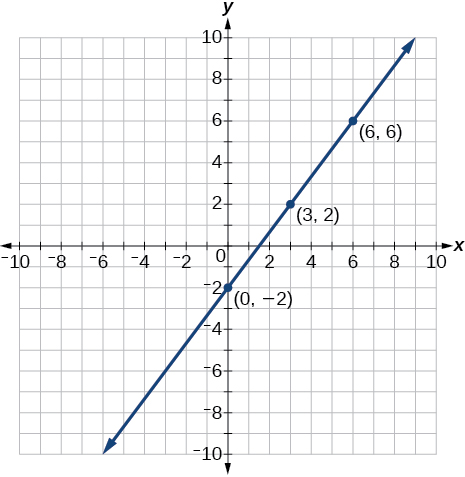
For the following exercises, construct a table and graph the equation by plotting at least three points.

  1. [latex]y=\frac{1}{2}x+4[/latex]
  1. [latex]4x-3y=6[/latex]
Show Solution
 
x y
0 −2
3 2
6 6

A coordinate plane with the x and y axes ranging from -10 to 10. The points (0,-2); (3,2) and (6,6) are plotted and a line runs through all these points.

 

Linear Equations in One Variable

For the following exercises, solve for [latex]\,x.[/latex]

  1. [latex]5x+2=7x-8[/latex]
  1. [latex]3\left(x+2\right)-10=x+4[/latex]
Show Solution

[latex]x=4[/latex]

  1. [latex]7x-3=5[/latex]
  1. [latex]12-5\left(x+1\right)=2x-5[/latex]
Show Solution

[latex]x=\frac{12}{7}[/latex]

  1. [latex]\frac{2x}{3}-\frac{3}{4}=\frac{x}{6}+\frac{21}{4}[/latex]

For the following exercises, solve for [latex]\,x.\,[/latex] State all x-values that are excluded from the solution set.

  1. [latex]\frac{x}{{x}^{2}-9}+\frac{4}{x+3}=\frac{3}{{x}^{2}-9}\,[/latex][latex]x\ne 3,-3[/latex]
Show Solution

No solution

  1. [latex]\frac{1}{2}+\frac{2}{x}=\frac{3}{4}[/latex]

Models and Applications

For the following exercises, write and solve an equation to answer each question.

  1. The number of males in the classroom is five more than three times the number of females. If the total number of students is 73, how many of each gender are in the class?
Show Solution

females 17, males 56

  1. A man has 72 ft. of fencing to put around a rectangular garden. If the length is 3 times the width, find the dimensions of his garden.
  1. A truck rental is $25 plus $.30/mi. Find out how many miles Ken traveled if his bill was $50.20.
Show Solution

84 mi

Complex Numbers

For the following exercises, use the quadratic equation to solve.

  1. [latex]{x}^{2}-5x+9=0[/latex]
  1. [latex]2{x}^{2}+3x+7=0[/latex]
Show Solution

[latex]x=\frac{-3}{4}±\frac{i\sqrt{47}}{4}[/latex]

For the following exercises, name the horizontal component and the vertical component.

  1. [latex]4-3i[/latex]
  1. [latex]-2-i[/latex]
Show Solution

horizontal component[latex]\,-2;[/latex] vertical component[latex]\,-1[/latex]

For the following exercises, perform the operations indicated.

  1. [latex]\left(9-i\right)-\left(4-7i\right)[/latex]
  1. [latex]\left(2+3i\right)-\left(-5-8i\right)[/latex]
Show Solution

[latex]7+11i[/latex]

  1. [latex]2\sqrt{-75}+3\sqrt{25}[/latex]
  1. [latex]\sqrt{-16}+4\sqrt{-9}[/latex]
Show Solution

[latex]16i[/latex]

  1. [latex]-6i\left(i-5\right)[/latex]
  1. [latex]{\left(3-5i\right)}^{2}[/latex]
Show Solution

[latex]-16-30i[/latex]

  1. [latex]\sqrt{-4}·\sqrt{-12}[/latex]
  1. [latex]\sqrt{-2}\left(\sqrt{-8}-\sqrt{5}\right)[/latex]
Show Solution

[latex]-4-i\sqrt{10}[/latex]

  1. [latex]\frac{2}{5-3i}[/latex]
  1. [latex]\frac{3+7i}{i}[/latex]
Show Solution

[latex]x=7-3i[/latex]

Quadratic Equations

For the following exercises, solve the quadratic equation by factoring.

  1. [latex]2{x}^{2}-7x-4=0[/latex]
  1. [latex]3{x}^{2}+18x+15=0[/latex]
Show Solution

[latex]x=-1,-5[/latex]

  1. [latex]25{x}^{2}-9=0[/latex]
  1. [latex]7{x}^{2}-9x=0[/latex]
Show Solution

[latex]x=0,\frac{9}{7}[/latex]

For the following exercises, solve the quadratic equation by using the square-root property.

  1. [latex]{x}^{2}=49[/latex]
  1. [latex]{\left(x-4\right)}^{2}=36[/latex]
Show Solution

[latex]x=10,-2[/latex]

For the following exercises, solve the quadratic equation by completing the square.

  1. [latex]{x}^{2}+8x-5=0[/latex]
  1. [latex]4{x}^{2}+2x-1=0[/latex]
Show Solution

[latex]x=\frac{-1±\sqrt{5}}{4}[/latex]

For the following exercises, solve the quadratic equation by using the quadratic formula. If the solutions are not real, state No real solution.

  1. [latex]2{x}^{2}-5x+1=0[/latex]
  1. [latex]15{x}^{2}-x-2=0[/latex]
Show Solution

[latex]x=\frac{2}{5},\frac{-1}{3}[/latex]

For the following exercises, solve the quadratic equation by the method of your choice.

  1. [latex]{\left(x-2\right)}^{2}=16[/latex]
  1. [latex]{x}^{2}=10x+3[/latex]
Show Solution

[latex]x=5±2\sqrt{7}[/latex]

Other Types of Equations

For the following exercises, solve the equations.

  1. [latex]{x}^{\frac{3}{2}}=27[/latex]
  1. [latex]{x}^{\frac{1}{2}}-4{x}^{\frac{1}{4}}=0[/latex]
Show Solution

[latex]x=0,256[/latex]

  1. [latex]4{x}^{3}+8{x}^{2}-9x-18=0[/latex]
  1. [latex]3{x}^{5}-6{x}^{3}=0[/latex]
Show Solution

[latex]x=0,±\sqrt{2}[/latex]

  1. [latex]\sqrt{x+9}=x-3[/latex]
  1. [latex]\sqrt{3x+7}+\sqrt{x+2}=1[/latex]
Show Solution

[latex]x=-2[/latex]

  1. [latex]|3x-7|=5[/latex]
  1. [latex]|2x+3|-5=9[/latex]
Show Solution

[latex]x=\frac{11}{2},\frac{-17}{2}[/latex]

Linear Inequalities and Absolute Value Inequalities

For the following exercises, solve the inequality. Write your final answer in interval notation.

  1. [latex]5x-8\le 12[/latex]
  1. [latex]-2x+5>x-7[/latex]
Show Solution

[latex]\left(-\infty ,4\right)[/latex]

  1. [latex]\frac{x-1}{3}+\frac{x+2}{5}\le \frac{3}{5}[/latex]
  1. [latex]|3x+2|+1\le 9[/latex]
Show Solution

[latex]\left[\frac{-10}{3},2\right][/latex]

  1. [latex]|5x-1|>14[/latex]
  1. [latex]|x-3|<-4[/latex]
Show Solution

No solution

For the following exercises, solve the compound inequality. Write your answer in interval notation.

  1. [latex]-4<3x+2\le 18[/latex]
  1. [latex]3y<1-2y<5+y[/latex]
Show Solution

[latex]\left(-\frac{4}{3},\frac{1}{5}\right)[/latex]

For the following exercises, graph as described.

  1. Graph the absolute value function and graph the constant function. Observe the points of intersection and shade the x-axis representing the solution set to the inequality. Show your graph and write your final answer in interval notation. [latex]|x+3|\ge 5[/latex]
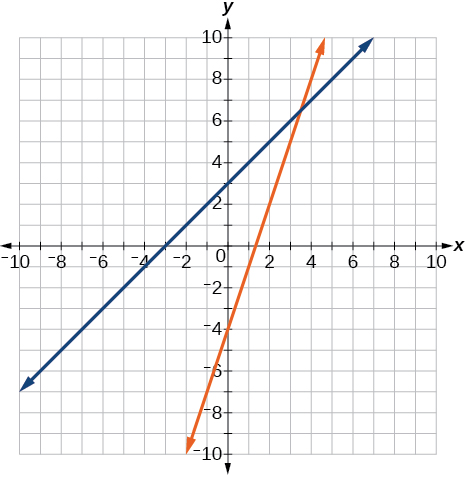
  1. Graph both straight lines (left-hand side being y1 and right-hand side being y2) on the same axes. Find the point of intersection and solve the inequality by observing where it is true comparing the y-values of the lines. See the interval where the inequality is true. [latex]x+3<3x-4[/latex]
Show Solution

Where the blue is below the orange line; point of intersection is [latex]\,x=3.5.[/latex]

[latex]\left(3.5,\infty \right)[/latex]
A coordinate plane with the x and y axes ranging from -10 to 10. The lines y = x + 3 and y = 3x -4 graphed on the same axes.

 

Media Attributions

License

Icon for the Creative Commons Attribution 4.0 International License

College Algebra Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book