Chapter 3 Functions

Chapter 3 Practice Test

For the following exercises, determine whether each of the following relations is a function.

  1. [latex]y=2x+8[/latex]
Show Solution

The relation is a function.

  1. [latex]\left\{\left(2,1\right),\left(3,2\right),\left(-1,1\right),\left(0,-2\right)\right\}[/latex]

For the following exercises, evaluate the function[latex]\,f\left(x\right)=-3{x}^{2}+2x\,[/latex] at the given input.

  1. [latex]f\left(-2\right)[/latex]
Show Solution

−16

  1. [latex]\,f\left(a\right)\,[/latex]
  1. Show that the function [latex]\,f\left(x\right)=-2{\left(x-1\right)}^{2}+3\,[/latex] is not one-to-one.
Show Solution

The graph is a parabola and the graph fails the horizontal line test.

  1. Write the domain of the function [latex]\,f\left(x\right)=\sqrt{3-x}\,[/latex] in interval notation.
  1. Given[latex]\,f\left(x\right)=2{x}^{2}-5x,\,[/latex] find [latex]f\left(a+1\right)-f\left(1\right)\,[/latex] in simplest form.
Show Solution

[latex]2{a}^{2}-a[/latex]

  1. Graph the function [latex]f(x) = \bigg\{\begin{array}{l} x +1 \text{ } \ \ \ -2< x<3\\ -x \text{ } \ \ \ \ \ \ \ \ \ \ x\ge 3\end{array}[/latex].
  1. Find the average rate of change of the function [latex]\,f\left(x\right)=3-2{x}^{2}+x\,[/latex] by finding[latex]\,\frac{f\left(b\right)-f\left(a\right)}{b-a}\,[/latex] in simplest form.
Show Solution

[latex]-2\left(a+b\right)+1[/latex]

For the following exercises, use the functions [latex]\,f\left(x\right)=3-2{x}^{2}+x\text{ and }g\left(x\right)=\sqrt{x}\,[/latex] to find the composite functions.

  1. [latex]\left(g\circ f\right)\left(x\right)[/latex]
  1. [latex]\left(g\circ f\right)\left(1\right)[/latex]
Show Solution

[latex]\sqrt{2}[/latex]

  1. Express[latex]\,H\left(x\right)=\sqrt[3]{5{x}^{2}-3x}\,[/latex]as a composition of two functions,[latex]\,f\,[/latex]and[latex]\,g,\,[/latex]where[latex]\,\left(f\circ g\right)\left(x\right)=H\left(x\right).[/latex]

For the following exercises, graph the functions by translating, stretching, and/or compressing a toolkit function.

  1. [latex]f\left(x\right)=\sqrt{x+6}-1[/latex]
Show Solution

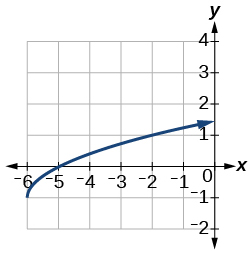
Graph of f(x)

 

  1. [latex]f\left(x\right)=\frac{1}{x+2}-1[/latex]

For the following exercises, determine whether the functions are even, odd, or neither.

  1. [latex]f\left(x\right)=-\frac{5}{{x}^{2}}+9{x}^{6}[/latex]
Show Solution

[latex]\text{even}[/latex]

  1. [latex]f\left(x\right)=-\frac{5}{{x}^{3}}+9{x}^{5}[/latex]
  1. [latex]f\left(x\right)=\frac{1}{x}[/latex]
Show Solution

[latex]\text{odd}[/latex]

  1. Graph the absolute value function[latex]\,f\left(x\right)=-2|x-1|+3.[/latex]

For the following exercises, find the inverse of the function.

  1. [latex]f\left(x\right)=3x-5[/latex]
Show Solution

[latex]{f}^{-1}\left(x\right)=\frac{x+5}{3}[/latex]

  1. [latex]f\left(x\right)=\frac{4}{x+7}[/latex]

For the following exercises, use the graph of [latex]\,g\,[/latex]shown in Figure below.

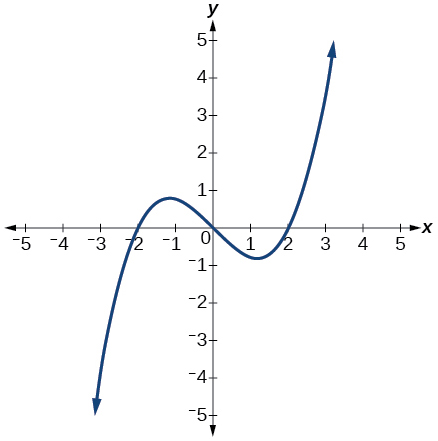
Graph of a cubic function.

  1. On what intervals is the function increasing?
Show Solution

[latex]\left(-\infty ,-1.1\right)\text{ and }\left(1.1,\infty \right)[/latex]

  1. On what intervals is the function decreasing?
  1. Approximate the local minimum of the function. Express the answer as an ordered pair.
Show Solution

[latex]\left(1.1,-0.9\right)[/latex]

  1. Approximate the local maximum of the function. Express the answer as an ordered pair.

For the following exercises, use the graph of the piecewise function shown in the Figure below.

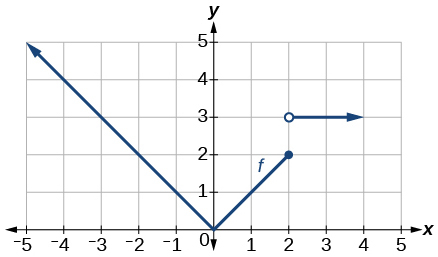
Ch-3-Practice-Test-24

  1. Find[latex]\,f\left(2\right).[/latex]
Show Solution

[latex]f\left(2\right)=2[/latex]

  1. Find[latex]\,f\left(-2\right).[/latex]
  1. Write an equation for the piecewise function.
Show Solution

[latex]f\left(x\right)=\bigg\{\begin{array}{l} | x | \text{ } \ \ \ \ \ x<2\\ 3 \text{ } \ \ \ \ \ \ \ \ x\ge 2\end{array}[/latex]

For the following exercises, use the values listed in Table 1.

Table 1
[latex]x[/latex] 0 1 2 3 4 5 6 7 8
[latex]F(x)[/latex] 1 3 5 7 9 11 13 15 17
  1. Find[latex]\,F\left(6\right).[/latex]
  1. Solve the equation[latex]\,F\left(x\right)=5.[/latex]
Show Solution

[latex]x=2[/latex]

  1. Is the graph increasing or decreasing on its domain?
  1. Is the function represented by the graph one-to-one?
Show Solution

yes

  1. Find[latex]\,{F}^{-1}\left(15\right).[/latex]
  1. Given[latex]\,f\left(x\right)=-2x+11,\,[/latex]find[latex]\,{f}^{-1}\left(x\right).[/latex]
Show Solution

[latex]{f}^{-1}\left(x\right)=-\frac{x-11}{2}[/latex]

Media Attributions

License

Icon for the Creative Commons Attribution 4.0 International License

College Algebra Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book