Chapter 5 Polynomial and Rational Functions
Chapter 5 Practice Test
Chapter Test
Give the degree and leading coefficient of the following polynomial function.
1. [latex]f\left(x\right)={x}^{3}\left(3-6{x}^{2}-2{x}^{2}\right)[/latex]
Determine the end behavior of the polynomial function.
2. [latex]f\left(x\right)=8{x}^{3}-3{x}^{2}+2x-4[/latex]
Show Solution
[latex]As\,x\to -\infty ,\,f\left(x\right)\to -\infty ,\,as\,x\to \infty ,\,f\left(x\right)\to \infty[/latex]
3. [latex]f\left(x\right)=-2{x}^{2}\left(4-3x-5{x}^{2}\right)[/latex]
Write the quadratic function in standard form. Determine the vertex and axes intercepts and graph the function.
4. [latex]f\left(x\right)={x}^{2}+2x-8[/latex]
Show Solution
[latex]f\left(x\right)={\left(x+1\right)}^{2}-9[/latex], vertex[latex]\,\left(-1,-9\right)[/latex], intercepts[latex]\,\left(2,0\right);\left(-4,0\right);\,\left(0,-8\right)[/latex]
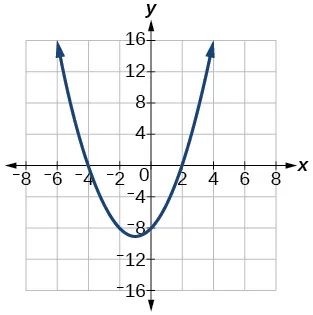
Given information about the graph of a quadratic function, find its equation.
5. Vertex[latex]\,\left(2,0\right)\,[/latex]and point on graph[latex]\,\left(4,12\right).[/latex]
Solve the following application problem.
6. A rectangular field is to be enclosed by fencing. In addition to the enclosing fence, another fence is to divide the field into two parts, running parallel to two sides. If 1,200 feet of fencing is available, find the maximum area that can be enclosed.
Show Solution
60,000 square feet
Find all zeros of the following polynomial functions, noting multiplicities.
7. [latex]f\left(x\right)={\left(x-3\right)}^{3}\left(3x-1\right){\left(x-1\right)}^{2}[/latex]
8. [latex]f\left(x\right)=2{x}^{6}-12{x}^{5}+18{x}^{4}[/latex]
Show Solution
0 with multiplicity 4, 3 with multiplicity 2
Based on the graph, determine the zeros of the function and multiplicities.
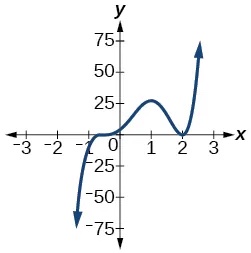
Use long division to find the quotient.
10. [latex]\frac{2{x}^{3}+3x-4}{x+2}[/latex]
Show Solution
[latex]2{x}^{2}-4x+11-\frac{26}{x+2}[/latex]
Use synthetic division to find the quotient. If the divisor is a factor, write the factored form.
11. [latex]\frac{{x}^{4}+3{x}^{2}-4}{x-2}[/latex]
12. [latex]\frac{2{x}^{3}+5{x}^{2}-7x-12}{x+3}[/latex]
Show Solution
[latex]2{x}^{2}-x-4[/latex]. So factored form is[latex]\,\left(x+3\right)\left(2{x}^{2}-x-4\right)[/latex]
Use the Rational Zero Theorem to help you find the zeros of the polynomial functions.
13. [latex]f\left(x\right)=2{x}^{3}+5{x}^{2}-6x-9[/latex]
14. [latex]f\left(x\right)=4{x}^{4}+8{x}^{3}+21{x}^{2}+17x+4[/latex]
Show Solution
[latex]-\frac{1}{2}\,[/latex]
(has multiplicity 2),[latex]\,\frac{-1±i\sqrt{15}}{2}\,[/latex]
16. [latex]f\left(x\right)={x}^{5}+6{x}^{4}+13{x}^{3}+14{x}^{2}+12x+8[/latex]
Show Solution
[latex]\,-2\,[/latex](has multiplicity 3),[latex]\,±i[/latex]
Given the following information about a polynomial function, find the function.
17. It has a double zero at[latex]\,x=3\,[/latex]and zeros at[latex]\,x=1\,[/latex]and[latex]\,x=-2\,[/latex]. Its y-intercept is[latex]\,\left(0,12\right).\,[/latex]
18. It has a zero of multiplicity 3 at[latex]\,x=\frac{1}{2}\,[/latex]and another zero at[latex]\,x=-3\,[/latex]. It contains the point[latex]\,\left(1,8\right).[/latex]
Show Solution
[latex]f\left(x\right)=2{\left(2x-1\right)}^{3}\left(x+3\right)[/latex]
Use Descartes’ Rule of Signs to determine the possible number of positive and negative solutions.
For the following rational functions, find the intercepts and horizontal and vertical asymptotes, and sketch a graph.
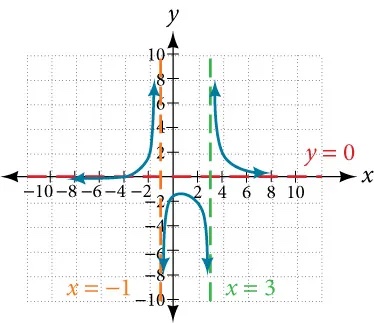
20. [latex]f\left(x\right)=\frac{x+4}{{x}^{2}-2x-3}[/latex]
Show Solution
Intercepts[latex]\,\left(-4,0\right),\,\left(0,-\frac{4}{3}\right)\,[/latex], Asymptotes[latex]\,x=3,\text{ }x\text{ }=-1,\text{ }y=0[/latex].
21. [latex]f\left(x\right)=\frac{{x}^{2}+2x-3}{{x}^{2}-4}[/latex]
Find the slant asymptote of the rational function.
22. [latex]f\left(x\right)=\frac{{x}^{2}+3x-3}{x-1}[/latex]
Show Solution
[latex]y=x+4[/latex]
Find the inverse of the function.
23. [latex]f\left(x\right)=\sqrt{x-2}+4[/latex]
24. [latex]f\left(x\right)=3{x}^{3}-4[/latex]
Show Solution
[latex]{f}^{-1}\left(x\right)=\sqrt[3]{\frac{x+4}{3}}[/latex]
25. [latex]f\left(x\right)=\frac{2x+3}{3x-1}[/latex]
Find the unknown value.
26. [latex]\,y\,[/latex]varies inversely as the square of[latex]\,x\,[/latex]and when[latex]\,x=3,\,[/latex][latex]y=2.\,[/latex]Find[latex]\,y\,[/latex]if[latex]\,x=1.[/latex]
Show Solution
[latex]y=18[/latex]
27. [latex]\,y\,[/latex]varies jointly with[latex]\,x\,[/latex]and the cube root of[latex]\,z.\,[/latex]If when[latex]\,x=2\,[/latex]and[latex]\,z=27,\,[/latex][latex]y=12,\,[/latex]find[latex]\,y\,[/latex]if[latex]\,x=5\,[/latex]and[latex]\,z=8.[/latex]
Solve the following application problem.
28. The distance a body falls varies directly as the square of the time it falls. If an object falls 64 feet in 2 seconds, how long will it take to fall 256 feet?
Show Solution
4 seconds
Media Attributions
- Ch 5 Practice Test #4 © OpenStax PreCalculus is licensed under a CC BY (Attribution) license
- Ch 5 Practice Test #9 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
- Ch 5 Practice Test # 20 © OpenStax Precalculus, 2e is licensed under a CC BY (Attribution) license

