Chapter 5 Polynomial and Rational Functions
Chapter 5 Review Exercises
Quadratic Functions
For the following exercises, write the quadratic function in standard form. Then give the vertex and axes intercepts. Finally, graph the function.
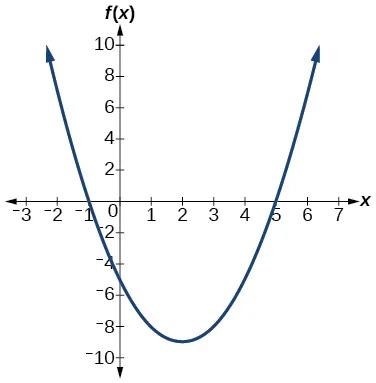
1. [latex]f\left(x\right)={x}^{2}-4x-5[/latex]
Show Solution
[latex]f\left(x\right)={\left(x-2\right)}^{2}-9\,\text{vertex} \left(2,–9\right), \text{intercepts} \left(5,0\right); \left(–1,0\right); \left(0,–5\right)[/latex]
2. [latex]f\left(x\right)=-2{x}^{2}-4x[/latex]
For the following exercises, find the equation of the quadratic function using the given information.
3. The vertex is[latex]\left(–2,3\right)[/latex]and a point on the graph is[latex]\,\left(3,6\right).[/latex]
Show Solution
[latex]f\left(x\right)=\frac{3}{25}{\left(x+2\right)}^{2}+3[/latex]
4. The vertex is[latex]\,\left(–3,6.5\right)\,[/latex]and a point on the graph is[latex]\,\left(2,6\right).[/latex]
For the following exercises, complete the task.
5. A rectangular plot of land is to be enclosed by fencing. One side is along a river and so needs no fence. If the total fencing available is 600 meters, find the dimensions of the plot to have maximum area.
Show Solution
300 meters by 150 meters, the longer side parallel to the river.
6. An object projected from the ground at a 45 degree angle with initial velocity of 120 feet per second has height,[latex]\,h,\,[/latex]in terms of horizontal distance traveled,[latex]\,x,\,[/latex]given by[latex]\,h\left(x\right)=\frac{-32}{{\left(120\right)}^{2}}{x}^{2}+x.\,[/latex]Find the maximum height the object attains.
Power Functions and Polynomial Functions
For the following exercises, determine if the function is a polynomial function, and if so, give the degree and leading coefficient.
7. [latex]f\left(x\right)=4{x}^{5}-3{x}^{3}+2x-1[/latex]
Show Solution
Yes, degree = 5, leading coefficient = 4
8. [latex]f\left(x\right)={5}^{x+1}-{x}^{2}[/latex]
9. [latex]f\left(x\right)={x}^{2}\left(3-6x+{x}^{2}\right)[/latex]
Show Solution
Yes, degree = 4, leading coefficient = 1
For the following exercises, determine end behavior of the polynomial function.
10. [latex]f\left(x\right)=2{x}^{4}+3{x}^{3}-5{x}^{2}+7[/latex]
11. [latex]f\left(x\right)=4{x}^{3}-6{x}^{2}+2[/latex]
Show Solution
[latex]\text{As}\,x\to -\infty ,\,f\left(x\right)\to -\infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to \infty[/latex]
12. [latex]f\left(x\right)=2{x}^{2}\left(1+3x-{x}^{2}\right)[/latex]
Graphs of Polynomial Functions
For the following exercises, find all zeros of the polynomial function, noting multiplicities.
13. [latex]f\left(x\right)={\left(x+3\right)}^{2}\left(2x-1\right){\left(x+1\right)}^{3}[/latex]
Show Solution
–3 with multiplicity 2,[latex]-\frac{1}{2}[/latex]with multiplicity 1, –1 with multiplicity 3
14. [latex]f\left(x\right)={x}^{5}+4{x}^{4}+4{x}^{3}[/latex]
15. [latex]f\left(x\right)={x}^{3}-4{x}^{2}+x-4[/latex]
Show Solution
4 with multiplicity 1
For the following exercises, based on the given graph, determine the zeros of the function and note multiplicity.
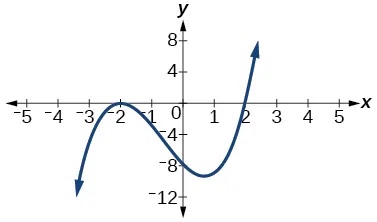
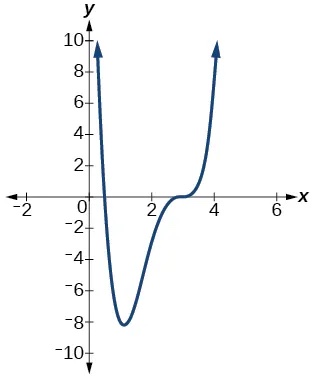
Show Solution
[latex]\frac{1}{2}\,[/latex]with multiplicity 1, 3 with multiplicity 3
18. Use the Intermediate Value Theorem to show that at least one zero lies between 2 and 3 for the function[latex]\,f\left(x\right)={x}^{3}-5x+1[/latex]
Dividing Polynomials
For the following exercises, use long division to find the quotient and remainder.
19. [latex]\frac{{x}^{3}-2{x}^{2}+4x+4}{x-2}[/latex]
Show Solution
[latex]\,{x}^{2}+4\,[/latex] with remainder 12
20. [latex]\frac{3{x}^{4}-4{x}^{2}+4x+8}{x+1}[/latex]
For the following exercises, use synthetic division to find the quotient. If the divisor is a factor, then write the factored form.
21. [latex]\frac{{x}^{3}-2{x}^{2}+5x-1}{x+3}[/latex]
Show Solution
[latex]{x}^{2}-5x+20-\frac{61}{x+3}[/latex]
22. [latex]\frac{{x}^{3}+4x+10}{x-3}[/latex]
23. [latex]\frac{2{x}^{3}+6{x}^{2}-11x-12}{x+4}[/latex]
Show Solution
[latex]2{x}^{2}-2x-3[/latex], so factored form is [latex]\left(x+4\right)\left(2{x}^{2}-2x-3\right)[/latex]
24. [latex]\frac{3{x}^{4}+3{x}^{3}+2x+2}{x+1}[/latex]
Zeros of Polynomial Functions
For the following exercises, use the Rational Zero Theorem to help you solve the polynomial equation.
25. [latex]2{x}^{3}-3{x}^{2}-18x-8=0[/latex]
Show Solution
[latex]\left\{-2, 4, -\frac{1}{2}\right\}[/latex]
26. [latex]3{x}^{3}+11{x}^{2}+8x-4=0[/latex]
27. [latex]2{x}^{4}-17{x}^{3}+46{x}^{2}-43x+12=0[/latex]
Show Solution
[latex]\left\{1, 3, 4, \frac{1}{2}\right\}[/latex]
28. [latex]4{x}^{4}+8{x}^{3}+19{x}^{2}+32x+12=0[/latex]
For the following exercises, use Descartes’ Rule of Signs to find the possible number of positive and negative solutions.
29. [latex]{x}^{3}-3{x}^{2}-2x+4=0[/latex]
Show Solution
0 or 2 positive, 1 negative
30. [latex]2{x}^{4}-{x}^{3}+4{x}^{2}-5x+1=0[/latex]
Rational Functions
For the following exercises, find the intercepts and the vertical and horizontal asymptotes, and then use them to sketch a graph of the function.
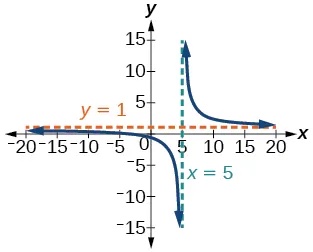
31. [latex]f\left(x\right)=\frac{x+2}{x-5}[/latex]
Show Solution
Intercepts [latex]\left(–2,0\right)\text{and}\left(0,-\frac{2}{5}\right)[/latex], Asymptotes[latex]\,x=5\,[/latex]
and[latex]\,y=1.[/latex]
32. [latex]f\left(x\right)=\frac{{x}^{2}+1}{{x}^{2}-4}[/latex]
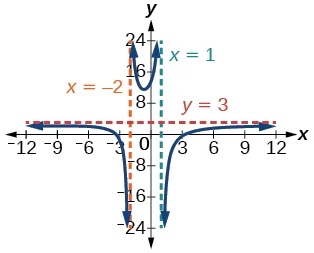
33. [latex]f\left(x\right)=\frac{3{x}^{2}-27}{{x}^{2}+x-2}[/latex]
Show Solution
Intercepts (3, 0), (-3, 0), and[latex]\,\left(0,\frac{27}{2}\right)\,[/latex], Asymptotes[latex]\,x=1, x=–2, y=3.[/latex]
For the following exercises, find the slant asymptote.
Show Solution
[latex]y=\text{ }x-2[/latex]
36. [latex]f\left(x\right)=\frac{2{x}^{3}-{x}^{2}+4}{{x}^{2}+1}[/latex]
Media Attributions
- Ch 5 Review #1 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- Ch 5 Review #16 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- Ch 5 Review #17 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license
- Ch 5 Review #31 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- Ch 5 Review #33 © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license

