Chapter 4 Linear Functions
4.1 Linear Equations in Two Variables
Learning Objectives
In this section, you will:
- Write a linear equation in two variables
- Given the equations of two lines, determine whether their graphs are parallel or perpendicular.
- Write the equation of a line parallel or perpendicular to a given line.
Write a Linear Equation in Two Variables
Perhaps the most familiar form of a linear equation is the slope-intercept form, written as[latex]\,y=mx+b,[/latex] where[latex]\,m=\text{slope}\,[/latex]and[latex]\,b=y\text{−intercept}\text{.}\,[/latex]Let us begin with the slope.
The Slope of a Line
The slope of a line refers to the ratio of the vertical change in y over the horizontal change in x between any two points on a line. It indicates the direction in which a line slants as well as its steepness. Slope is sometimes described as rise over run.
The Slope of a Line
The slope of a line, m, represents the change in y over the change in x. Given two points,[latex]\,\left({x}_{1},{y}_{1}\right)\,[/latex]and[latex]\,\left({x}_{2},{y}_{2}\right),[/latex] the following formula determines the slope of a line containing these points:
Finding the Slope of a Line Given Two Points
Find the slope of a line that passes through the points[latex]\,\left(2,-1\right)\,[/latex]and[latex]\,\left(-5,3\right).[/latex]
Show Solution
We substitute the y-values and the x-values into the formula.
The slope is[latex]\,-\frac{4}{7}.[/latex]
Analysis
It does not matter which point is called[latex]\,\left({x}_{1},{y}_{1}\right)\,[/latex]or[latex]\,\left({x}_{2},{y}_{2}\right).\,[/latex]As long as we are consistent with the order of the y terms and the order of the x terms in the numerator and denominator, the calculation will yield the same result.
Try It
Find the slope of the line that passes through the points[latex]\,\left(-2,6\right)\,[/latex]and[latex]\,\left(1,4\right).[/latex]
Show Solution
[latex]m=-\frac{2}{3}[/latex]
Identifying the Slope and y-intercept of a Line Given an Equation
Identify the slope and y-intercept, given the equation[latex]\,y=-\frac{3}{4}x-4.[/latex]
Show Solution
As the line is in[latex]\,y=mx+b\,[/latex]form, the given line has a slope of[latex]\,m=-\frac{3}{4}.\,[/latex]The y-intercept is[latex]\,b=-4.[/latex]
Analysis
The y-intercept is the point at which the line crosses the y-axis. On the y-axis,[latex]\,x=0.\,[/latex]We can always identify the y-intercept when the line is in slope-intercept form, as it will always equal b. Or, just substitute[latex]\,x=0\,[/latex]and solve for y.
The Point-Slope Formula
Given the slope and one point on a line, we can find the equation of the line using the point-slope formula.
This is an important formula, as it will be used in other areas of college algebra and often in calculus to find the equation of a tangent line. We need only one point and the slope of the line to use the formula. After substituting the slope and the coordinates of one point into the formula, we simplify it and write it in slope-intercept form.
The Point-Slope Formula
Given one point and the slope, the point-slope formula will lead to the equation of a line:
Finding the Equation of a Line Given the Slope and One Point
Write the equation of the line with slope[latex]\,m=-3\,[/latex]and passing through the point[latex]\,\left(4,8\right).\,[/latex]Write the final equation in slope-intercept form.
Show Solution
Using the point-slope formula, substitute[latex]\,-3\,[/latex]for m and the point[latex]\,\left(4,8\right)\,[/latex]for[latex]\,\left({x}_{1},{y}_{1}\right).[/latex]
Analysis
Note that any point on the line can be used to find the equation. If done correctly, the same final equation will be obtained.
Try It
Given[latex]\,m=4,[/latex] find the equation of the line in slope-intercept form passing through the point[latex]\,\left(2,5\right).[/latex]
Show Solution
[latex]y=4x-3[/latex]
Finding the Equation of a Line Passing Through Two Given Points
Find the equation of the line passing through the points[latex]\,\left(3,4\right)\,[/latex]and[latex]\,\left(0,-3\right).\,[/latex]Write the final equation in slope-intercept form.
Show Solution
First, we calculate the slope using the slope formula and two points.
Next, we use the point-slope formula with the slope of[latex]\,\frac{7}{3},[/latex] and either point. Let’s pick the point[latex]\,\left(3,4\right)\,[/latex]for[latex]\,\left({x}_{1},{y}_{1}\right).[/latex]
In slope-intercept form, the equation is written as[latex]\,y=\frac{7}{3}x-3.[/latex]
Analysis
To prove that either point can be used, let us use the second point[latex]\,\left(0,-3\right)\,[/latex]and see if we get the same equation.
We see that the same line will be obtained using either point. This makes sense because we used both points to calculate the slope.
Standard Form of a Line
Another way that we can represent the equation of a line is in standard form. Standard form is given as
where[latex]\,A,[/latex][latex]B,[/latex] and[latex]\,C[/latex]are integers. The x- and y-terms are on one side of the equal sign and the constant term is on the other side.
Finding the Equation of a Line and Writing It in Standard Form
Find the equation of the line with[latex]\,m=-6\,[/latex]and passing through the point[latex]\,\left(\frac{1}{4},-2\right).\,[/latex]Write the equation in standard form.
Show Solution
We begin using the point-slope formula.
Try It
Find the equation of the line in standard form with slope[latex]\,m=-\frac{1}{3}\,[/latex]and passing through the point[latex]\,\left(1,\frac{1}{3}\right).[/latex]
Show Solution
[latex]x+3y=2[/latex]
Vertical and Horizontal Lines
The equations of vertical and horizontal lines do not require any of the preceding formulas, although we can use the formulas to prove that the equations are correct. The equation of a vertical line is given as
where c is a constant. The slope of a vertical line is undefined, and regardless of the y-value of any point on the line, the x-coordinate of the point will be c.
Suppose that we want to find the equation of a line containing the following points:[latex]\,\left(-3,-5\right),\left(-3,1\right),\left(-3,3\right),[/latex] and[latex]\,\left(-3,5\right).\,[/latex]First, we will find the slope.
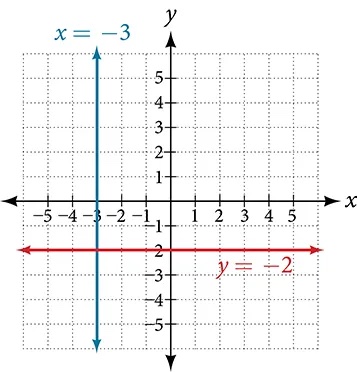
Zero in the denominator means that the slope is undefined, and therefore, we cannot use the point-slope formula. However, we can plot the points. Notice that all of the x-coordinates are the same and we find a vertical line through[latex]\,x=-3.\,[/latex]See Figure 2.
The equation of a horizontal line is given as
where c is a constant. The slope of a horizontal line is zero, and for any x-value of a point on the line, the y-coordinate will be c.
Suppose we want to find the equation of a line that contains the following set of points:[latex]\,\left(-2,-2\right),\left(0,-2\right),\left(3,-2\right),[/latex] and[latex]\,\left(5,-2\right).[/latex]We can use the point-slope formula. First, we find the slope using any two points on the line.
Use any point for[latex]\,\left({x}_{1},{y}_{1}\right)\,[/latex]in the formula, or use the y-intercept.
The graph is a horizontal line through[latex]\,y=-2.\,[/latex]Notice that all of the y-coordinates are the same. See Figure 2.
Finding the Equation of a Line Passing Through the Given Points
Find the equation of the line passing through the given points:[latex]\,\left(1,-3\right)\,[/latex]and[latex]\,\left(1,4\right).[/latex]
Show Solution
The x-coordinate of both points is 1. Therefore, we have a vertical line,[latex]\,x=1.[/latex]
Try It
Find the equation of the line passing through[latex]\,\left(-5,2\right)\,[/latex]and[latex]\,\left(2,2\right).[/latex]
Show Solution
Horizontal line:[latex]\,y=2[/latex]
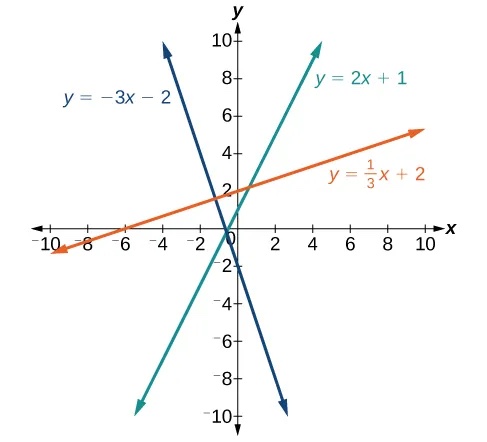
Determining Whether Graphs of Lines Are Parallel or Perpendicular
Parallel lines have the same slope and different y-intercepts. Lines that are parallel to each other will never intersect. For example, Figure 3 shows the graphs of various lines with the same slope,[latex]\,m=2.[/latex]
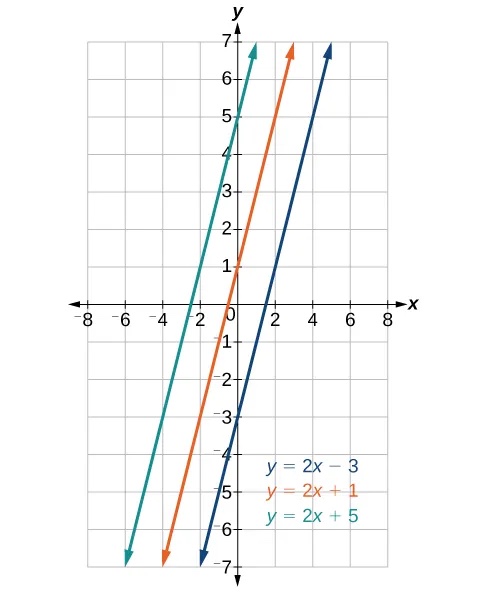
All of the lines shown in the graph are parallel because they have the same slope and different y-intercepts.
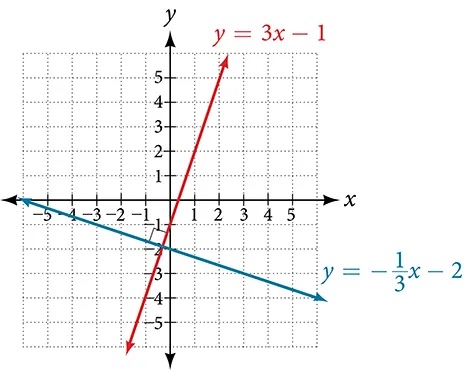
Lines that are perpendicular intersect to form a[latex]\,90°[/latex] angle. The slope of one line is the negative reciprocal of the other. We can show that two lines are perpendicular if the product of the two slopes is[latex]\,-1:{m}_{1}\cdot {m}_{2}=-1.\,[/latex]For example, Figure 4 shows the graph of two perpendicular lines. One line has a slope of 3; the other line has a slope of[latex]\,-\frac{1}{3}.[/latex]
Graphing Two Equations, and Determining Whether the Lines Are Parallel, Perpendicular, or Neither
Graph the equations of the given lines, and state whether they are parallel, perpendicular, or neither:[latex]\,3y=-4x+3\,[/latex]and[latex]\,3x-4y=8.[/latex]
Show Solution
The first thing we want to do is rewrite the equations so that both equations are in slope-intercept form.
First equation:
Second equation:
See the graph of both lines in Figure 5.
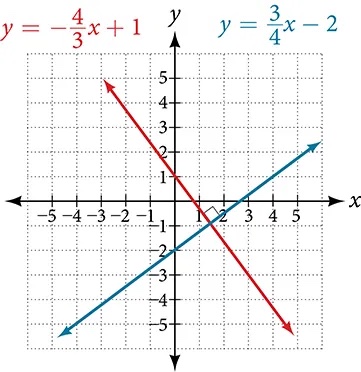
From the graph, we can see that the lines appear perpendicular, but we must compare the slopes.
The slopes are negative reciprocals of each other, confirming that the lines are perpendicular.
Try It
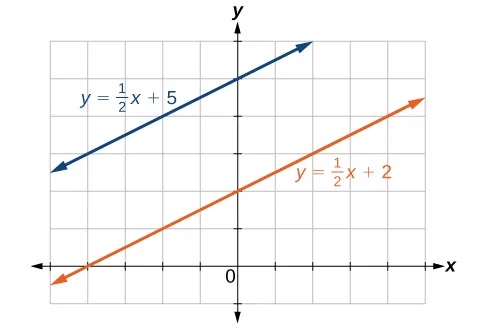
Graph the two lines and determine whether they are parallel, perpendicular, or neither:[latex]\,2y-x=10\,[/latex]and[latex]\,2y=x+4.[/latex]
Show Solution
Parallel lines: equations are written in slope-intercept form.
Writing the Equations of Lines Parallel or Perpendicular to a Given Line
As we have learned, determining whether two lines are parallel or perpendicular is a matter of finding the slopes. To write the equation of a line parallel or perpendicular to another line, we follow the same principles as we do for finding the equation of any line. After finding the slope, use the point-slope formula to write the equation of the new line.
How To
Given an equation for a line, write the equation of a line parallel or perpendicular to it.
- Find the slope of the given line. The easiest way to do this is to write the equation in slope-intercept form.
- Use the slope and the given point with the point-slope formula.
- Simplify the line to slope-intercept form and compare the equation to the given line.
Writing the Equation of a Line Parallel to a Given Line Passing Through a Given Point
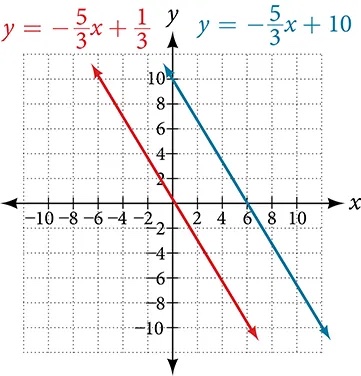
Write the equation of line parallel to a[latex]\,5x+3y=1\,[/latex]and passing through the point[latex]\,\left(3,5\right).[/latex]
Show Solution
First, we will write the equation in slope-intercept form to find the slope.
The slope is[latex]\,m=-\frac{5}{3}.\,[/latex]The y-intercept is[latex]\,\frac{1}{3},[/latex]but that really does not enter into our problem, as the only thing we need for two lines to be parallel is the same slope. The one exception is that if the y-intercepts are the same, then the two lines are the same line. The next step is to use this slope and the given point with the point-slope formula.
The equation of the line is[latex]\,y=-\frac{5}{3}x+10.\,[/latex]See Figure 6.
Try It
Find the equation of the line parallel to[latex]\,5x=7+y\,[/latex]and passing through the point[latex]\,\left(-1,-2\right).[/latex]
Show Solution
[latex]y=5x+3[/latex]
Finding the Equation of a Line Perpendicular to a Given Line Passing Through a Given Point
Find the equation of the line perpendicular to[latex]\,5x-3y+4=0\,\,\left(-4,1\right).[/latex]
Show Solution
The first step is to write the equation in slope-intercept form.
We see that the slope is[latex]\,m=\frac{5}{3}.\,[/latex]This means that the slope of the line perpendicular to the given line is the negative reciprocal, or [latex]-\frac{3}{5}.\,[/latex]Next, we use the point-slope formula with this new slope and the given point.
Key Concepts
- Given two points, we can find the slope of a line using the slope formula.
- We can identify the slope and y-intercept of an equation in slope-intercept form.
- We can find the equation of a line given the slope and a point.
- We can also find the equation of a line given two points. Find the slope and use the point-slope formula.
- The standard form of a line has no fractions.
- Horizontal lines have a slope of zero and are defined as[latex]\,y=c,[/latex] where c is a constant.
- Vertical lines have an undefined slope (zero in the denominator) and are defined as[latex]\,x=c,[/latex] where c is a constant.
- Parallel lines have the same slope and different y-intercepts.
- Perpendicular lines have slopes that are negative reciprocals of each other unless one is horizontal and the other is vertical.
- A line parallel to another line, passing through a given point, may be found by substituting the slope value of the line and the x– and y-values of the given point into the equation,[latex]\,f\left(x\right)=mx+b,\,[/latex]and using the[latex]\,b\,[/latex]that results. Similarly, the point-slope form of an equation can also be used.
- A line perpendicular to another line, passing through a given point, may be found in the same manner, with the exception of using the negative reciprocal slope.
Section Exercises
Verbal
- What does it mean when we say that two lines are parallel?
Show Solution
It means they have the same slope.
- What is the relationship between the slopes of perpendicular lines (assuming neither is horizontal nor vertical)?
- How do we recognize when an equation, for example[latex]\,y=4x+3,[/latex] will be a straight line (linear) when graphed?
Show Solution
The exponent of the[latex]\,x\,[/latex]variable is 1. It is called a first-degree equation.
Algebraic
For the following exercises, find the equation of the line using the point-slope formula. Write all the final equations using the slope-intercept form.
- [latex]\left(0,3\right)\,[/latex]with a slope of[latex]\,\frac{2}{3}[/latex]
- [latex]\left(1,2\right)\,[/latex]with a slope of[latex]\,\frac{-4}{5}[/latex]
Show Solution
[latex]y=\frac{-4}{5}x+\frac{14}{5}[/latex]
- x-intercept is 1, and[latex]\,\left(-2,6\right)[/latex]
- y-intercept is 2, and[latex]\,\left(4,-1\right)[/latex]
Show Solution
[latex]y=\frac{-3}{4}x+2[/latex]
- [latex]\left(-3,10\right)\,[/latex]and[latex]\,\left(5,-6\right)[/latex]
- [latex]\left(1,3\right)\text{ and }\left(5,5\right)[/latex]
Show Solution
[latex]y=\frac{1}{2}x+\frac{5}{2}[/latex]
- parallel to[latex]\,y=2x+5\,[/latex]and passes through the point[latex]\,\left(4,3\right)[/latex]
- perpendicular to[latex]\,\text{3}y=x-4\,[/latex]and passes through the point[latex]\,\left(-2,1\right)[/latex].
Show Solution
[latex]y=-3x-5[/latex]
For the following exercises, find the equation of the line using the given information.
- [latex]\left(-2,0\right)\,[/latex]and[latex]\,\left(-2,5\right)[/latex]
- [latex]\left(1,7\right)\,[/latex]and[latex]\,\left(3,7\right)[/latex]
Show Solution
[latex]y=7[/latex]
- The slope is undefined and it passes through the point[latex]\,\left(2,3\right).[/latex]
- The slope equals zero and it passes through the point[latex]\,\left(1,-4\right).[/latex]
Show Solution
[latex]y=-4[/latex]
- The slope is[latex]\,\frac{3}{4}\,[/latex]and it passes through the point[latex]\,\text{(1,4)}\text{.}[/latex]
- [latex]\left(-1,3\right)\,[/latex]and[latex]\,\left(4,-5\right)[/latex]
Show Solution
[latex]8x+5y=7[/latex]
Graphical
For the following exercises, graph the pair of equations on the same axes, and state whether they are parallel, perpendicular, or neither.
- [latex]\begin{array}{l}\\ \begin{array}{l}y=2x+7\hfill \\ y=\frac{-1}{2}x-4\hfill \end{array}\end{array}[/latex]
- [latex]\begin{array}{l}3x-2y=5\hfill \\ 6y-9x=6\hfill \end{array}[/latex]
Show Solution
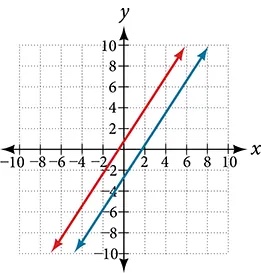
Parallel
- [latex]\begin{array}{l}y=\frac{3x+1}{4}\hfill \\ y=3x+2\hfill \end{array}[/latex]
- [latex]\begin{array}{l}x=4\\ y=-3\end{array}[/latex]
Show Solution
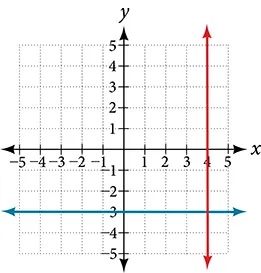
Perpendicular
Numeric
For the following exercises, find the slope of the line that passes through the given points.
- [latex]\left(5,4\right)\,[/latex]and[latex]\,\left(7,9\right)[/latex]
- [latex]\left(-3,2\right)\,[/latex]and[latex]\,\left(4,-7\right)[/latex]
Show Solution
[latex]m=\frac{-9}{7}[/latex]
- [latex]\left(-5,4\right)\,[/latex]and[latex]\,\left(2,4\right)[/latex]
- [latex]\left(-1,-2\right)\,[/latex]and[latex]\,\left(3,4\right)[/latex]
Show Solution
[latex]m=\frac{3}{2}[/latex]
- [latex]\,\left(3,-2\right)[/latex]and[latex]\,\left(3,-2\right)[/latex]
For the following exercises, find the slope of the lines that pass through each pair of points and determine whether the lines are parallel or perpendicular.
- [latex]\begin{array}{l}\left(-1,3\right)\text{ and }\left(5,1\right)\\ \left(-2,3\right)\text{ and }\left(0,9\right)\end{array}[/latex]
Show Solution
[latex]{m}_{1}=\frac{-1}{3},\text{ }{m}_{2}=3;\text{ }\text{Perpendicular}\text{.}[/latex]
- [latex]\begin{array}{l}\left(2,5\right)\text{ and }\left(5,9\right)\\ \left(-1,-1\right)\text{ and }\left(2,3\right)\end{array}[/latex]
Technology
For the following exercises, express the equations in slope intercept form (rounding each number to the thousandths place). Enter this into a graphing calculator as Y1, then adjust the ymin and ymax values for your window to include where the y-intercept occurs. State your ymin and ymax values.
- [latex]0.537x-2.19y=100[/latex]
Show Solution
[latex]y=0.245x-45.662.\,[/latex]Answers may vary.[latex]\,{y}_{\text{min}}=-50,\text{ }{y}_{\text{max}}=-40[/latex]
- [latex]4,500x-200y=9,528[/latex]
- [latex]\frac{200-30y}{x}=70[/latex]
Show Solution
[latex]y=-2.333x+6.667.\,[/latex]Answers may vary.[latex]\,{y}_{\mathrm{min}}=-10, {y}_{\mathrm{max}}=10[/latex]
Extensions
- Starting with the point-slope formula[latex]\,y-{y}_{1}=m\left(x-{x}_{1}\right),[/latex]solve this expression for[latex]\,x\,[/latex]in terms of[latex]\,{x}_{1},y,{y}_{1},[/latex]and[latex]\,m.[/latex]
- Starting with the standard form of an equation[latex]\,\text{A}x\text{ + B}y\text{ = C,}[/latex] solve this expression for y in terms of[latex]\,A,B,C,\,[/latex]and[latex]\,x.\,[/latex]Then put the expression in slope-intercept form.
Show Solution
[latex]y=\frac{-A}{B}x+\frac{C}{B}[/latex]
- Use the above derived formula to put the following standard equation in slope intercept form:[latex]\,7x-5y=25.[/latex]
- Given that the following coordinates are the vertices of a rectangle, prove that this truly is a rectangle by showing the slopes of the sides that meet are perpendicular.
[latex]\left(-1,1\right),\left(2,0\right),\left(3,3\right)\text{,}[/latex]and[latex]\,\left(0,4\right)[/latex]
Show Solution
[latex]\begin{array}{l}\text{The slope for }\left(-1,1\right)\text{ to }\left(0,4\right)\text{ is }3.\\ \text{The slope for }\left(-1,1\right)\text{ to }\left(2,0\right)\text{ is }\frac{-1}{3}.\\ \text{The slope for }\left(2,0\right)\text{ to }\left(3,3\right)\text{ is }3.\\ \text{The slope for }\left(0,4\right)\text{ to }\left(3,3\right)\text{ is }\frac{-1}{3}.\end{array}[/latex]
Yes they are perpendicular.
- Find the slopes of the diagonals in the previous exercise. Are they perpendicular?
Real-World Applications
- The slope for a wheelchair ramp for a home has to be[latex]\,\frac{1}{12}.\,[/latex]If the vertical distance from the ground to the door bottom is 2.5 ft, find the distance the ramp has to extend from the home in order to comply with the needed slope.
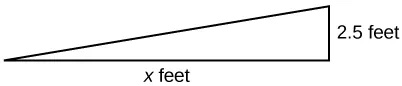
Show Solution
30 ft
- If the profit equation for a small business selling[latex]\,x\,[/latex]number of item one and[latex]\,y\,[/latex]number of item two is[latex]\,p=3x+4y,[/latex] find the[latex]\,y\,[/latex]value when[latex]\,p=\text{\$}453\text{ and }x=75.[/latex]
For the following exercises, use this scenario: The cost of renting a car is $45/wk plus $0.25/mi traveled during that week. An equation to represent the cost would be[latex]\,y=45+.25x,[/latex] where[latex]\,x\,[/latex]is the number of miles traveled.
- What is your cost if you travel 50 mi?
Show Solution
$57.50
- If your cost were[latex]\,\text{\$}63.75,[/latex] how many miles were you charged for traveling?
- Suppose you have a maximum of $100 to spend for the car rental. What would be the maximum number of miles you could travel?
Show Solution
220 mi
Glossary
- linear equation
- an algebraic equation in which each term is either a constant or the product of a constant and the first power of a variable
- slope
- the change in y-values over the change in x-values
Media Attributions
- 4.1 Figure 1 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 4.1 Figure 2 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 4.1 Figure 3 Parallel Lines © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 4.1 Figure 4 Perpendicular Lines © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 4.1 Figure 5 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 4.1 Graph of Parallel Lines © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 4.1 Figure 6 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 4.1 Exercise #19 Solution © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 4.1 Exercise #21 Solution © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
- 4.1 Exercise #37 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license

