10.4 Polar Form for Complex Numbers
The figure below shows the complex number [latex]z=3+3i\text{,}[/latex] represented as a vector in the complex plane. The distance [latex]r[/latex] from the origin to [latex]z[/latex] is
[latex]r=\sqrt{3^2+3^2} = 3\sqrt{2}[/latex]
and the angle from the real axis to the vector is [latex]\theta=\dfrac{\pi}{4}\text{.}[/latex]
Using right triangle trigonometry, we see that
[latex]a = 3\sqrt{2}\cos \dfrac{\pi}{4} = 3\sqrt{2} \cdot \dfrac{1}{\sqrt{2}} = 3\\ b = 3\sqrt{2} \sin \dfrac{\pi}{4} = 3\sqrt{2} \cdot \dfrac{1}{\sqrt{2}} = 3[/latex]

In general, we can write the real and imaginary parts of [latex]z[/latex] in terms of [latex]r[/latex] and [latex]\theta[/latex] as
[latex]a=r \cos \theta~~~~\text{and}~~~~b=r\sin \theta[/latex]
Thus, the complex number [latex]z=a+bi[/latex] can also be written as
[latex]z=(r\cos\theta)+(r\sin \theta)i~~~~\text{or}~~~~z=r(\cos\theta+i\sin \theta)\text{.}[/latex]
Find the polar form for [latex]z=\sqrt{3} + i\text{.}[/latex]
Solution
We compute
[latex]r=\sqrt{a^2+b^2} = \sqrt{3+1} = 2~~~~\text{and}~~~~\tan \theta = \dfrac{1}{\sqrt{3}}[/latex]
The angle [latex]\theta[/latex] is in the first quadrant, so
[latex]\theta = \tan^{-1} \dfrac{1}{\sqrt{3}} = \dfrac{\pi}{6}[/latex]

Thus,[latex]~~z= 2(\cos \dfrac{\pi}{6} + i\sin \dfrac{\pi}{6})[/latex]
The complex number [latex]z=a+bi[/latex] can be written in the polar form
[latex]z=r\left(\cos\theta+i\sin \theta\right)[/latex]
where [latex]~~r=\sqrt{a^2+b^2}~~[/latex] and [latex]\theta[/latex] is defined by
[latex]a=r \cos \theta,~~~~b=r\sin \theta,~~~~0 \le \theta \le 2\pi[/latex]
The angle [latex]\theta[/latex] is called the argument of the complex number, and [latex]r[/latex] is its length, or modulus.
Checkpoint 10.64.
Find the polar form for [latex]w=1+i\sqrt{3}\text{.}[/latex]
Solution
[latex]w=2\left(\cos \dfrac{\pi}{3} + i\sin \dfrac{\pi}{3}\right)[/latex]
Of course, we can always recover the Cartesian form of a complex number from its polar form by evaluating the trigonometric functions. We’ll check the result of the previous example:
[latex]z = 2(\cos \dfrac{\pi}{6} + i\sin \dfrac{\pi}{6})\\ = 2(\dfrac{\sqrt{3}}{2} + i \cdot \dfrac{1}{2} = \sqrt{3} + i[/latex]
The polar form is especially convenient for computing the product or quotient of two complex numbers.
If [latex]z_1=r(\cos \alpha+i\sin \alpha)[/latex] and [latex]z_2=R(\cos \beta+i\sin \beta)\text{,}[/latex] then
[latex]{z_1z_2=rR(\cos (\alpha + \beta) + i \sin (\alpha + \beta))}[/latex]
This formula, which you will prove in the Homework Problems, says that the product of two complex numbers in polar form is the complex number with modulus [latex]rR[/latex] and argument [latex]\alpha + \beta\text{.}[/latex] Thus, to find the product of two complex numbers, we multiply their lengths and add their arguments.
Find the product of [latex]z= 2\left(\cos \dfrac{\pi}{6} + i\sin \dfrac{\pi}{6}\right)[/latex] and [latex]w= 2\left(\cos \dfrac{\pi}{3} + i\sin \dfrac{\pi}{3}\right)\text{.}[/latex]
Solution
We multiply the moduli, [latex]2 \cdot 2 =4\text{,}[/latex] and add the arguments, [latex]\dfrac{\pi}{6}+\dfrac{\pi}{3} = \dfrac{\pi}{2}\text{.}[/latex] The polar form of the product is thus
[latex]zw=4\left(\cos \dfrac{\pi}{2} + i\sin \dfrac{\pi}{2}\right) = 4i[/latex]
Note that [latex]z[/latex] and [latex]w[/latex] are the numbers from the previous example and exercise; namely, [latex]z=\sqrt{3} + i[/latex] and [latex]w=1+i\sqrt{3}\text{.}[/latex] You can compute the product [latex]zw[/latex] in Cartesian form to check that you get the same result, [latex]4i\text{.}[/latex]
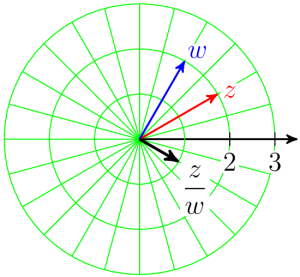
The figure shows the graphs of [latex]z[/latex] and [latex]w[/latex] and their product, [latex]zw\text{.}[/latex] You can see that multiplying [latex]z[/latex] by [latex]w[/latex] rotates the graph of [latex]z[/latex] by the argument of [latex]w\text{,}[/latex] namely [latex]\dfrac{\pi}{3}[/latex] or [latex]60°\text{.}[/latex]
Checkpoint 10.66.
- Find the polar forms of [latex]z=3+3i[/latex] and [latex]w=-2+2i\text{.}[/latex]
- Compute the product [latex]zw\text{.}[/latex]
Solution
- [latex]z=3\sqrt{2}\left(\cos \dfrac{\pi}{4} + i\sin \dfrac{\pi}{4}\right)\text{,}[/latex] [latex]~w=2\sqrt{2}\left(\cos \dfrac{5\pi}{4} + i\sin \dfrac{5\pi}{4}\right)[/latex]
- [latex]\displaystyle -12i[/latex]
The quotient of two complex numbers in polar form is computed in a similar fashion.
If [latex]z_1=r(\cos \alpha+i\sin \alpha)[/latex] and [latex]z_2=R(\cos \beta+i\sin \beta)\text{,}[/latex] then
[latex]{ \dfrac{z_1}{z_2}=\dfrac{r}{R}(\cos (\alpha - \beta) + i \sin (\alpha - \beta))}[/latex]
Find the quotient of [latex]z= 2\left(\cos \dfrac{\pi}{6} + i\sin \dfrac{\pi}{6}\right)[/latex] and [latex]w= 2\left(\cos \dfrac{\pi}{3} + i\sin \dfrac{\pi}{3}\right)\text{.}[/latex]
Solution
We divide the moduli, [latex]\dfrac{2}{2} = 1\text{,}[/latex] and subtract the arguments, [latex]\dfrac{\pi}{6}-\dfrac{\pi}{3} = \dfrac{-\pi}{6}\text{.}[/latex]
The polar form of the quotient is thus
[latex]\dfrac{z}{w}=1\left(\cos \dfrac{-\pi}{6} + i\sin \dfrac{-\pi}{6}\right)=\dfrac{\sqrt{3}}{2} - \dfrac{1}{2} i[/latex]
The figure shows the graphs of [latex]z,~w\text{,}[/latex] and the quotient [latex]\dfrac{z}{w}\text{.}[/latex]
Checkpoint 10.68.
Compute the quotient [latex]\dfrac{z}{w}[/latex] for [latex]z=3+3i[/latex] and [latex]2=-2+2i\text{.}[/latex]
Solution
[latex]\dfrac{-3}{2}[/latex]
Because raising to a power is just repeated multiplication, we can also use the polar form to simplify powers of a complex number. For example, if [latex]z=r(\cos\alpha+i\sin \alpha)\text{,}[/latex] then
[latex]z^2=z \cdot z = r \cdot r(\cos(\alpha+ \alpha) +i\sin (\alpha + \alpha))[/latex]
We compute [latex]z^2[/latex] by squaring the modulus, [latex]r\text{,}[/latex] and doubling the argument, [latex]\alpha\text{,}[/latex] so the polar form is
[latex]z^2= r^2(\cos 2\alpha+i\sin 2\alpha)[/latex]
An analogous result holds for all positive integers [latex]n\text{,}[/latex] and is known as De Moivre’s theorem.
If [latex]z=r(\cos\alpha+i\sin \alpha)[/latex] is a complex number in polar form, and [latex]n[/latex] is a positive integer, then [latex]z^n= r^n(\cos n\alpha+i\sin n\alpha)[/latex]
Raise [latex]z=\sqrt{3} + i[/latex] to the fourth power.
Solution
We use the polar form, [latex]z= 2\left(\cos \dfrac{\pi}{6} + i\sin \dfrac{\pi}{6}\right)\text{,}[/latex] and apply De Moivre’s theorem. Then
[latex]z^4 = 2^4\left(\cos 4 \cdot \dfrac{\pi}{6}+i\sin 4 \cdot \dfrac{\pi}{6}\right)\\ =16\left(\cos \dfrac{2\pi}{3} + i\sin \dfrac{2\pi}{3}\right)[/latex]
The Cartesian form of [latex]z^4[/latex] is thus [latex]16\left(\dfrac{-1}{2} + i\dfrac{\sqrt{3}}{2}\right)\text{,}[/latex] or [latex]-8+8i\sqrt{3}\text{.}[/latex] You can check that you get this same result if you compute [latex]\left(\sqrt{3} + i\right)^4[/latex] by expanding the power.
Checkpoint 10.70.
Compute [latex]w^3\text{,}[/latex] for [latex]w=-\sqrt{2}+\sqrt{2}i\text{.}[/latex]
Solution
[latex]4\sqrt{2}+4\sqrt{2} i[/latex]
De Moivre’s theorem also works for fractional values of [latex]n\text{,}[/latex] so we can compute roots of complex numbers. For example, by applying the theorem with [latex]n=\dfrac{1}{2}\text{,}[/latex] we see that one of the square roots of [latex]z=r\left(\cos\alpha+i\sin \alpha\right)[/latex] is
[latex]z^{1/2}=r^{1/2}\left(\cos \dfrac{\alpha}{2}+i\sin \dfrac{\alpha}{2}\right)[/latex]
Now, every number, whether real or complex, has two square roots. To find the other root, remember that we can add a multiple of [latex]2\pi[/latex] to the argument of [latex]z\text{,}[/latex] that is, we can also write the polar form of [latex]z[/latex] as
[latex]z=r(\cos(\alpha+2\pi)+i\sin (\alpha+2\pi))[/latex]
The second square root of [latex]z[/latex] is thus
[latex]r^{1/2}\left(\cos (\dfrac{\alpha}{2}+\pi)+i\sin (\dfrac{\alpha}{2}+\pi)\right)[/latex]
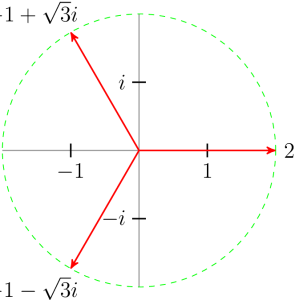
As an example consider [latex]w=-8+8i\sqrt{3},[/latex] whose polar form is [latex]16\left(\cos \dfrac{2\pi}{3} + i\sin \dfrac{2\pi}{3}\right)\text{,}[/latex] or by adding [latex]2\pi[/latex] to the argument, [latex]16\left(\cos \dfrac{8\pi}{3} + i\sin \dfrac{8\pi}{3}\right)\text{.}[/latex] The two square roots of [latex]w[/latex] are
[latex]z_1 = 16^{1/2}\left(\cos \dfrac{\pi}{3} + i\sin \dfrac{\pi}{3}\right)=4\left(\dfrac{1}{2} + i\dfrac{\sqrt{3}}{2}\right) = 2+2i\sqrt{3}[/latex]
[latex]z_2=16^{1/2}\left(\cos \dfrac{4\pi}{3} + i\sin \dfrac{4\pi}{3}\right)=4\left(\dfrac{-1}{2} + i\dfrac{-\sqrt{3}}{2}\right) = -2-2i\sqrt{3}[/latex]
You can verify that both of these numbers are square roots of [latex]w=-8+8i\sqrt{3}\text{,}[/latex] for instance,
[latex]\left(2+2i\sqrt{3}\right)^2 = 4+2(2)\left(2i\sqrt{3}\right)+12i^2\\ =-8+8i\sqrt{3}[/latex]
The graphs of [latex]w[/latex] and its two square roots are shown at right.

It is not hard to show that every number has three complex cube roots, four complex fourth roots, and so on.
Find three complex cube roots of [latex]8\text{.}[/latex]
Solution
One polar form of [latex]z=8[/latex] is [latex]z=8(\cos 0 + i \sin 0)[/latex] so one of its cube roots is [latex]z_1=8^{1/3}\left(\cos \dfrac{0}{3} + i \sin \dfrac{0}{3}\right) = 2(\cos 0 + i \sin 0) = 2[/latex]
But by adding multiples of [latex]2\pi[/latex] to the argument, we can also write the polar form of as
[latex]z=8(\cos 2\pi + i \sin 2\pi)~~~~\text{and}~~~~z=8(\cos 4\pi + i \sin 4\pi)[/latex]
Applying De Moivre’s theorem to each of these expressions gives us two more cube roots
[latex]z_2 = 2\left(\cos \dfrac{2\pi}{3} + i\sin \dfrac{2\pi}{3}\right) = -1+i\sqrt{3}[/latex]
[latex]z_3 = 2\left(\cos \dfrac{4\pi}{3} + i\sin \dfrac{4\pi}{3}\right)= -1-i\sqrt{3}[/latex]
The three roots are shown. Note that they are evenly spaced around a circle of radius 2. You can check that adding further multiples of [latex]2\pi[/latex] to the argument does not generate any new cube roots.
A complex number [latex]z=r(\cos \alpha + i\sin \alpha)[/latex] in polar form has [latex]n[/latex] complex [latex]n[/latex]th roots, given by
[latex]z_k = r^{1/n}\left(\cos \dfrac{\alpha + 2\pi k}{n} + i\sin \dfrac{\alpha + 2\pi k}{n}\right)[/latex]
for [latex]k = 0,~1,~2, \cdots,~ n-1\text{.}[/latex]
Checkpoint 10.72.
- Write [latex]i[/latex] in polar form.
- Find four complex fourth roots of [latex]i\text{.}[/latex]
Solution
- [latex]\displaystyle \cos \dfrac{\pi}{2} + i\sin \dfrac{\pi}{2}[/latex]
- [latex]\cos \dfrac{\pi}{8} + i\sin \dfrac{\pi}{8}\text{,}[/latex] [latex]~ \cos \dfrac{5\pi}{8} + i\sin \dfrac{5\pi}{8}\text{,}[/latex] [latex]~ \cos \dfrac{9\pi}{8} + i\sin \dfrac{9\pi}{8}\text{,}[/latex] [latex]~ \cos \dfrac{13\pi}{8} + i\sin \dfrac{13\pi}{8}[/latex]
Vocabulary
Concepts
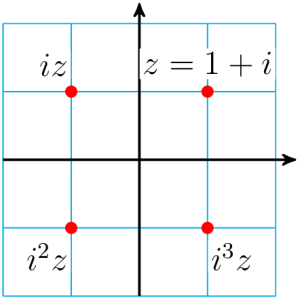
- Multiplying a complex number by [latex]i[/latex] rotates its graph by [latex]90°[/latex] around the origin.
-
Polar Form for a Complex Number.
The complex number [latex]z=a+bi[/latex] can be written in the polar form
[latex]z=r(\cos\theta+i\sin \theta)[/latex]
where
[latex]r=\sqrt{a^2+b^2}[/latex]
and [latex]\theta[/latex] is defined by
[latex]a=r \cos \theta,~~~~b=r\sin \theta,~~~~0 \le \theta \le 2\pi[/latex]
The angle [latex]\theta[/latex] is called the argument of the complex number, and [latex]r[/latex] is its length, or modulus.
-
Product and Quotient in Polar Form.
If [latex]z_1=r(\cos \alpha+i\sin \alpha)[/latex] and [latex]z_2=R(\cos \beta+i\sin \beta)\text{,}[/latex] then
[latex]z_1z_2=rR(\cos (\alpha + \beta) + i \sin (\alpha + \beta))[/latex]
and
[latex]\dfrac{z_1}{z_2}=\dfrac{r}{R}(\cos (\alpha - \beta) + i \sin (\alpha - \beta))[/latex]
-
De Moivre’s Theorem.
If [latex]z=r(\cos\alpha+i\sin \alpha)[/latex] is a complex number in polar form, and [latex]n[/latex] is a positive integer, then
[latex]z^n= r^n(\cos n\alpha+i\sin n\alpha)[/latex]
-
Roots of a Complex Number.
A complex number [latex]z=r(\cos \alpha + i\sin \alpha)[/latex] in polar form has [latex]n[/latex] complex [latex]n[/latex]th roots, given by
[latex]z_k = r^{1/n}\left(\cos \dfrac{\alpha + 2\pi k}{n} + i\sin \dfrac{\alpha + 2\pi k}{n}\right)[/latex]
for [latex]k = 0,~1,~2, \cdots,~ n-1\text{.}[/latex]
Study Questions
- What happens to the vector representing a complex number when we multiply the number by [latex]-i\text{?}[/latex]
- If [latex]z=p+qi\text{,}[/latex] what do these expressions represent? [latex]p^2+q^2,~ p-qi,~ \dfrac{q}{p}[/latex]
- If [latex]z_1[/latex] and [latex]z_2[/latex] lie on the unit circle, explain why [latex]z_1z_2[/latex] and [latex]\dfrac{z_1}{z_2}[/latex] also lie on the unit circle.
- Explain how you could use De Moivre’s theorem to compute [latex]z^{2/3}\text{.}[/latex]