Chapter 8: More Functions and Identities

Introduction to More Functions and Identities

Introduction

Mapmakers have always faced an unavoidable challenge: It is impossible to translate the surface of a sphere onto a flat map without some form of distortion. Over the years, a variety of map projections have been developed to suit different uses (Figure 1).

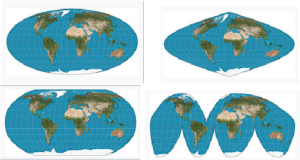
Four images showing techniques of making the surface of a sphere into a flat map.
Figure 1

The sixteenth century was an age of discovery, when explorers and merchants began sailing to distant and previously unknown lands. But at that time, there was no reliable technology for navigation. Although more regions of the world were being mapped more accurately, a flat map by itself was not enough to help a sailor in the middle of the ocean.

In 1569, the Flemish cartographer Gerardus Mercator published a new map using what is known as a cylindrical projection. To imagine how a Mercator projection works, picture shining a light through a glass globe onto a piece of paper rolled into a cylinder and wrapped around the globe. The cylinder is tangent to the globe at its equator (Figure 2).

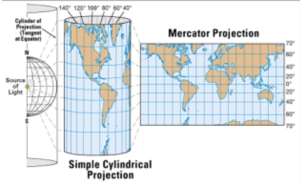
A simple cylindrical projection shown as a Mercator projection.
Figure 2

Notice how the latitude lines are farther apart the farther you get from the equator. This projection distorts the size of objects as the latitude increases so that Greenland and Antarctica appear much larger than they actually are (Figure 3).

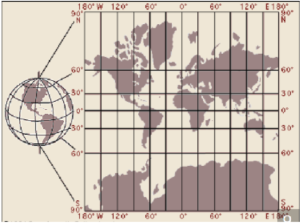
A map showing how the latitude lines from a sphere are projected onto a flat map.
Figure 3

But the Mercator projection map is ideally suited for navigation, because any straight line on the map is a line of constant true bearing. If a navigator measures the bearing on the map from his location to his destination, he can set his ship’s compass for the same bearing and maintain that course.

However, the Mercator projection does not preserve distances. On a globe, circles of latitude (also known as parallels) get smaller as they move away from the equator toward the poles. Thus, in the Mercator projection, when a globe is “unwrapped” onto a rectangular map, the parallels need to be stretched to the length of the equator. Mercator had to increase the scale of his map gradually as it moved away from the equator so that the latitude lines appear equal in length to the equator.

The horizontal scale factor at any latitude must be inversely proportional to lengths on that latitude. Because the radius of the circle of latitude [latex]\theta[/latex] is [latex]R\cos{\theta}[/latex], the corresponding parallel on the map must be stretched by a factor of [latex]\frac{1}{\cos{\theta}}[/latex]. And because the secant is the reciprocal of the cosine, the scale factor is proportional to the secant of the latitude.

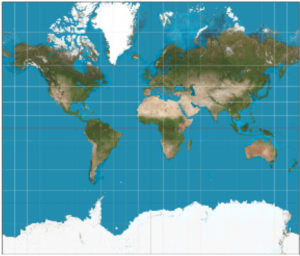
A variety of “equal area” projections have been developed in modern times, but the Mercator projection is still widely used in classrooms and atlases. For many people, it represents our image of the world (Figure 4).

A flat map of the Earth.
Figure 4

 

Class Activities

Activity 8.1. Negative Angles

I. Using Reference Triangles

    1. Suppose that [latex]\theta[/latex] is a first-quadrant angle. In which quadrant would you find [latex]-\theta{?}[/latex]
    2. Sketch an example for [latex]\theta{,}[/latex] [latex]-\theta{,}[/latex] and the reference triangle for each.
    3. How is [latex]\sin (-\theta)[/latex] related to [latex]\sin \theta{?}[/latex] What about [latex]\cos (-\theta)[/latex] and [latex]\tan (-\theta){?}[/latex]
  2. Repeat part (1) for the case where there is a second-quadrant angle.

II. Using Graphs

    1. Look at the graph of [latex]f(\theta) = \sin \theta{,}[/latex] and choose three positive values of [latex]\theta{.}[/latex] Draw dots on the graph that show their function values.sine graph
    2. Find the negatives of your three values of [latex]\theta[/latex] from part (a), and draw dots to show their function values.
    3. How do the values of [latex]\sin (-\theta)[/latex] compare to the values of [latex]\sin \theta{?}[/latex]
  2. Repeat part (1) for the graph of [latex]f(\theta) = \cos \theta{.}[/latex]cosine graph
  3. Repeat part (1) for the graph of [latex]f(\theta) = \tan \theta{.}[/latex]tangent graph

III. Negative Angle Identities
State your conclusions from parts I and II as identities:
[latex]\sin (-\theta) = \qquad\qquad[/latex]
[latex]\cos (-\theta) = \qquad\qquad[/latex]
[latex]\tan (-\theta) = \qquad\qquad[/latex]

 

Activity 8.2. Identities

Sum of Angles Identities
  1. Is it true that [latex]\cos (\theta + \phi) = \cos \theta + \cos \phi{?}[/latex] Try it for [latex]\theta = 60°[/latex] and [latex]\phi = 45°{.}[/latex]
    1. Recall the distributive law, [latex]a(b+c) = ab + ac{,}[/latex] where the parentheses denote multiplication. Is the same law true when the parentheses denote a function? In other words, is it true that [latex]f(a+b) = f(a) + f(b){?}[/latex]
    2. In the expression [latex]\sin (\theta + \phi){,}[/latex] do the parentheses denote multiplication or the application of a function? Does the distributive law apply to [latex]\sin (\theta + \phi){?}[/latex] Do you think that [latex]\sin (\theta + \phi) = \sin \theta + \sin \phi[/latex] is an identity?
    1. Look at the Sum of Angles Identities in this section. Make some observations that will help you memorize these formulas.
    2. Do you think you would have to memorize these formulas if the equation [latex]\sin (\theta + \phi) = \sin \theta + \sin \phi[/latex] were an identity?

Difference of Angles Identities, Tangent Identities

    1. Yikes! More formulas. Compare the Difference of Angles Identities with the Sum of Angles Identities. If you have memorized the Sum formulas, how can you also memorize the Difference formulas?
    2. Comment on the sign patterns in the Sum and Difference Identities for Tangent.
    1. Now let’s use the formulas backward. Look at the expression below:
      [latex]\dfrac{\tan 285° - \tan 75°}{1 + \tan 285° \tan 75°}[/latex]
      Does it remind you of the left side of one of the six new identities? Use that identity to simplify the expression.
    2. Do the same thing for this expression:
      [latex]\sin 4t \cos 0.7 - \cos 4t \sin 0.7[/latex]

Double Angle Identities

    1. Is it true that [latex]\sin 2\theta = 2\sin \theta{?}[/latex] Choose a value for [latex]\theta[/latex] and try it. Sketch [latex]\theta[/latex] and [latex]2\theta[/latex] on a unit circle and show the sine of each.
    2. Is it true that [latex]\cos 2\theta = 2\cos \theta{?}[/latex] Repeat part (a) for cosine.
    3. Substitute [latex]\alpha = \theta[/latex] and [latex]\beta = \theta[/latex] into the sum of angles formulas for sine, cosine, and tangent to derive the double angle formulas.
    4. Choose one of the three forms of the Double Angle Identity for Cosine. Use the Pythagorean Identity to convert from that form to each of the other two forms.

 

Activity 8.5. Reciprocal Ratios.

Part 1
The figure shows a unit circle centered at [latex]O{.}[/latex] The line through [latex]AC[/latex] is tangent to the circle at [latex]A{.}[/latex] (Recall that a tangent to a circle is perpendicular to the radius that meets it.)
unit circle

  1. What is the radius of the circle?
  2. Find line segments whose lengths are [latex]\cos \theta[/latex] and [latex]\sin \theta{.}[/latex]
  3. Explain why [latex]\triangle OAC[/latex] is similar to [latex]\triangle OBD{.}[/latex]
  4. Find a line segment in [latex]\triangle OAC[/latex] whose length is [latex]\tan \theta{.}[/latex] Explain why your choice is correct.
  5. Find a line segment in [latex]\triangle OAC[/latex] whose length is [latex]\sec \theta{.}[/latex] Explain why your choice is correct.
  6. Find a line segment in [latex]\triangle OAC[/latex] whose length is [latex]\csc \theta{.}[/latex] Explain why your choice is correct.

 

Part 2
Here is another unit circle, with tangent [latex]BD{.}[/latex]

unit circle

  1. What is the measure of the angles [latex]\angle OCD[/latex] and [latex]\angle OCB{?}[/latex]
  2. Explain why [latex]\triangle OCB[/latex] is similar to [latex]\triangle OAC{.}[/latex]
  3. Find a line segment in [latex]\triangle OCB[/latex] whose length is [latex]\tan \theta{.}[/latex] Explain why your choice is correct.
  4. Find a line segment in [latex]\triangle OCB[/latex] whose length is [latex]\sec \theta{.}[/latex] Explain why your choice is correct.
  5. Explain why [latex]\triangle OCB[/latex] is similar to [latex]\triangle DCO{.}[/latex]
  6. Find a line segment in [latex]\triangle DCO[/latex] whose length is [latex]\csc \theta{.}[/latex] Explain why your choice is correct.

Media Attributions

License

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Share This Book