Exercises Homework 6.2
Exercise Group
For Problems 1–4, each point on the unit circle is the terminal point of an angle in standard position. Give exact values for the radian measure, [latex]t{,}[/latex] of the angle and the coordinates [latex](x,y)[/latex] of the point.
1.

| [latex]\hphantom{0000}[/latex] |
a |
b |
c |
d |
| [latex]t[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]x[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]y[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
2.

| [latex]\hphantom{0000}[/latex] |
a |
b |
c |
d |
| [latex]t[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]x[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]y[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
3.

| [latex]\hphantom{0000}[/latex] |
a |
b |
c |
d |
| [latex]t[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]x[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]y[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
4.

| [latex]\hphantom{0000}[/latex] |
a |
b |
c |
d |
| [latex]t[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]x[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]y[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
Exercise Group
For Problems 5–8, use the unit circle to estimate the sine, cosine, and tangent of each arc of given length.

5.
- [latex]0.4[/latex]
- [latex]1.2[/latex]
- [latex]2[/latex]
6.
- [latex]0.8[/latex]
- [latex]2.6[/latex]
- [latex]4[/latex]
7.
- [latex]2.8[/latex]
- [latex]3.5[/latex]
- [latex]5[/latex]
8.
- [latex]3[/latex]
- [latex]4.3[/latex]
- [latex]5.5[/latex]
Exercise Group
For Problems 9–14, use the unit circle to estimate two numbers with the given trig value.

9.
[latex]\cos t = 0.3[/latex]
10.
[latex]\sin t = 0.1[/latex]
11.
[latex]\sin t = -0.7[/latex]
12.
[latex]\cos t = -0.6[/latex]
13.
[latex]\tan t = \dfrac{-4}{9}[/latex]
14.
[latex]\tan t = \dfrac{8}{6}[/latex]
Exercise Group
Each of Problems 13–20 describes an arc in standard position on the unit circle. In which quadrant does the terminal point of the arc lie?
15.
[latex]\sin s \gt 0,~ \cos s \lt 0[/latex]
16.
[latex]\sin s \lt 0,~ \cos s \gt 0[/latex]
17.
[latex]\cos t \lt 0,~ \tan t \lt 0[/latex]
18.
[latex]\cos t \gt 0,~ \tan t \lt 0[/latex]
19.
[latex]\sin x \lt 0,~ \tan x \gt 0[/latex]
20.
[latex]\sin x \gt 0,~ \tan x \lt 0[/latex]
Exercise Group
For Problems 21–26, without using a calculator, decide whether the quantity is positive or negative.
21.
[latex]\cos 2.7[/latex]
22.
[latex]\sin 4.1[/latex]
23.
[latex]\tan 3.8[/latex]
24.
[latex]\tan 5.4[/latex]
25.
[latex]\sin 2.2[/latex]
26.
[latex]\cos 4.9[/latex]
Exercise Group
For Problems 27–30, place the trig values in order from smallest to largest. Use the figure to help you, but try not to use a calculator!

27.
[latex]\sin 0.5,~ \sin 1.5,~ \sin 2.5,~ \sin 3.5[/latex]
28.
[latex]\cos 1.6,~ \cos 2.6,~ \cos 3.6,~ \cos 5.6[/latex]
29.
[latex]\cos 2,~ \cos 3,~ \cos 4,~ \cos 5[/latex]
30.
[latex]\sin 2.8,~ \sin 3.8,~ \sin 4.8,~ \sin 5.8[/latex]
31.
The sunrise time in Wellington, New Zealand, on the [latex]n[/latex]th day of the year can be modeled by
[latex]S = 1.93 \sin (0.016n - 1.13) + 6.14[/latex]
where [latex]S[/latex] is given in hours after midnight. Find the sunrise time on January 1 (day [latex]n = 1[/latex]), April 1 (day [latex]n = 91[/latex]), July 1 (day [latex]n = 182[/latex]), and October 1 (day [latex]n = 274[/latex]).
32.
The variable star RT Cygni reached its maximum magnitude on May 22, 2004, and [latex]t[/latex] days later, its magnitude is given by
[latex]M = 9.55 - 2.25 \cos (0.033t)[/latex]
Find the magnitude of RT Cygni on days [latex]t = 0,~ t = 48,~ t = 95,~ t = 142,[/latex] and [latex]t = 190{.}[/latex] (Note that smaller values of [latex]M[/latex] denote brighter magnitudes.)
Exercise Group
For Problems 33–38, find the reference angle in radians, rounded to two decimal places.
33.
[latex]1.8[/latex]
34.
[latex]4.9[/latex]
35.
[latex]-2.3[/latex]
36.
[latex]-6.0[/latex]
37.
[latex]9.4[/latex]
38.
[latex]7.1[/latex]
Exercise Group
For Problems 39–44, find the reference angle in radians, expressed as a multiple of [latex]\pi{.}[/latex]
39.
[latex]\dfrac{11\pi}{12}[/latex]
40.
[latex]\dfrac{11\pi}{8}[/latex]
41.
[latex]\dfrac{4\pi}{3}[/latex]
42.
[latex]\dfrac{7\pi}{6}[/latex]
43.
[latex]\dfrac{13\pi}{4}[/latex]
44.
[latex]\dfrac{8\pi}{3}[/latex]
45.
Find three angles in radians between [latex]0[/latex] and [latex]2\pi[/latex] with the given reference angle. Sketch all the angles on a unit circle.
- [latex]\dfrac{\pi}{6}[/latex]
- [latex]\dfrac{\pi}{4}[/latex]
- [latex]\dfrac{\pi}{3}[/latex]
46.
Complete the table.
| [latex]~\theta~[/latex] |
[latex]~~~\sin \theta~~~[/latex] |
[latex]~~~\cos \theta~~~[/latex] |
[latex]~~~\tan \theta~~~[/latex] |
| [latex]\dfrac{2\pi}{3}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]\dfrac{3\pi}{4}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]\dfrac{5\pi}{6}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
47.
Complete the table.
| [latex]~\theta~[/latex] |
[latex]~~~\sin \theta~~~[/latex] |
[latex]~~~\cos \theta~~~[/latex] |
[latex]~~~\tan \theta~~~[/latex] |
| [latex]\dfrac{7\pi}{6}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]\dfrac{5\pi}{4}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]\dfrac{4\pi}{3}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
48.
Complete the table.
| [latex]~\theta~[/latex] |
[latex]~~~\sin \theta~~~[/latex] |
[latex]~~~\cos \theta~~~[/latex] |
[latex]~~~\tan \theta~~~[/latex] |
| [latex]\dfrac{5\pi}{3}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]\dfrac{7\pi}{4}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
| [latex]\dfrac{11\pi}{6}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
[latex]\hphantom{0000}[/latex] |
Exercise Group
For Problems 49–54, evaluate the expression exactly.
49.
[latex]\cos \dfrac{\pi}{3} \sin \dfrac{\pi}{6}[/latex]
50.
[latex]\sin \dfrac{\pi}{4} \tan \dfrac{\pi}{3}[/latex]
51.
[latex]\tan \dfrac{5\pi}{6} + \tan \dfrac{7\pi}{4}[/latex]
52.
[latex]\cos \dfrac{3\pi}{4} - \cos \dfrac{5\pi}{3}[/latex]
53.
[latex]\cos^2 (\dfrac{11\pi}{6}) - 3\cos \dfrac{11\pi}{6}[/latex]
54.
[latex]2\sin \dfrac{4\pi}{3} - \sin^2 (\dfrac{4\pi}{3})[/latex]
Exercise Group
Starting at [latex](1,0){,}[/latex] you walk [latex]s[/latex] units around a unit circle. For Problems 55–58, sketch a unit circle showing your position. What are your coordinates?
55.
[latex]s = 2.5[/latex]
56.
[latex]s = 4.3[/latex]
57.
[latex]s = 8.5[/latex]
58.
[latex]s = 11[/latex]
59.
City Park features a circular jogging track of radius 1 mile, centered on the open-air bandstand. You start jogging on the track 1 mile due east of the bandstand and proceed counterclockwise. What are your coordinates, relative to the bandstand, when you have jogged five miles?
60.
Silver Reservoir is a circular man-made lake of radius 1 kilometer. If you start at the easternmost point on the reservoir and walk counterclockwise for 4 kilometers, how far south of your initial position are you?
Exercise Group
For Problems 61–66, find the angle in radians between [latex]0[/latex] and [latex]2\pi[/latex] determined by the terminal point on the unit circle. Round your answer to hundredths.
61.
[latex](-0.1782, 0.9840)[/latex]
62.
[latex](-0.8968, -0.4425)[/latex]
63.
[latex](0.8855, -0.4646)[/latex]
64.
[latex](0.9801, 0.1987)[/latex]
65.
[latex](-0.7659, -0.6430)[/latex]
66.
[latex](0.9602, -0.2794)[/latex]
67.
- Sketch a unit circle and the line [latex]y = x{.}[/latex] Find the coordinates of the two points where the line and the circle intersect.
- State your answers to part (a) using trigonometric functions.
68.
- Sketch a unit circle and the line [latex]y = -x{.}[/latex] Find the coordinates of the two points where the line and the circle intersect.
- State your answers to part (a) using trigonometric functions.
69.
- Sketch a line that passes through the origin and the point [latex](8,3){.}[/latex] What is the slope of the line?
- What is the angle of inclination of the line in radians, measured from the positive [latex]x[/latex]-axis?

70.
- Sketch a line that passes through the origin and the point [latex](3,8){.}[/latex] What is the slope of the line?
- What is the angle of inclination of the line in radians, measured from the positive [latex]x[/latex]-axis?

Exercise Group
For Problems 71–74, find an equation for the line with the given angle of inclination, passing through the given point. (See Section 4.3 to review angle of inclination.)
71.
[latex]\alpha = \dfrac{\pi}{3},~ (4,2)[/latex]
72.
[latex]\alpha = \dfrac{5\pi}{6},~ (-6,3)[/latex]
73.
[latex]\alpha = 2.4,~ (5,-8)[/latex]
74.
[latex]\alpha = 0.6,~ (-2,-3)[/latex]
75.
Use similar triangles to show that the coordinates of point [latex]P[/latex] on the unit circle shown at right are [latex](\cos t, \sin t){.}[/latex]

76.
Use similar triangles to show that [latex]ST = \tan t{.}[/latex]

Exercise Group
Use the results of Problem 77 for Problems 78–80.
77.
Use similar triangles to show that the coordinates of a point [latex]P[/latex] determined by angle [latex]\theta[/latex] on a circle of radius [latex]r[/latex] are [latex]x = r \cos \theta,~ y = r\sin \theta{.}[/latex] (See the figure at right.)

78.
The Astrodome in Houston has a diameter of 710 feet. If you start at the easternmost point and walk counterclockwise around its perimeter for a distance of 250 feet, how far north of your starting point are you?
79.
The Barringer meteor crater near Winslow, Arizona, is 1182 meters in diameter. You start at the easternmost point on the rim of the crater and walk counterclockwise around the edge. After walking for 1 kilometer, what is your position relative to your starting point?
80.
One of the most intriguing features of Stonehenge is the position of the four Station Stones.
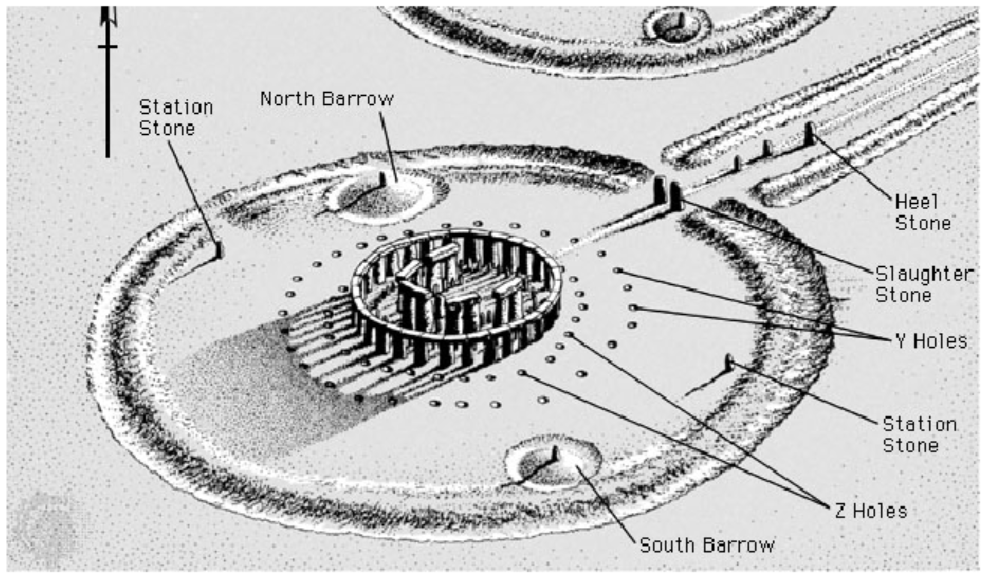
They form the corners of a rectangle inscribed in the Aubrey Circle on the perimeter of the henge, which has diameter 288 feet. A line from the center of the circle and perpendicular to the long edge of the rectangle points through the Slaughter Stones at the entrance of the henge and out to the Heel Stone. If you stood in the center of the circle on the summer solstice, you would see the sun rise directly over the Heel Stone.
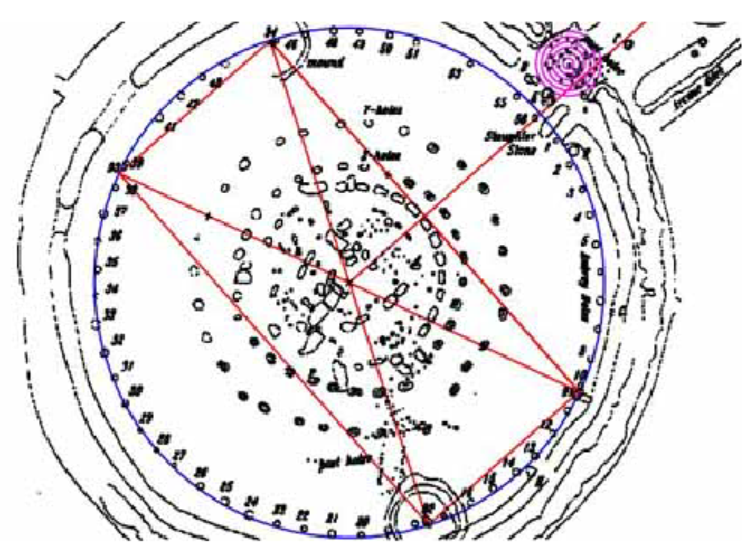
- The sun rises [latex]48.6°[/latex] east of north on the summer solstice at Stonehenge. If the positive [latex]y[/latex]-axis points north, find the coordinates of the henge entrance relative to its center.
- The northernmost station stone is located [latex]66.6°[/latex] of arc counterclockwise from the entrance. Find its coordinates relative to the center of the henge.


