Sum of angles in a triangle
The sum of the angles in a triangle is [latex]180^{\circ}[/latex].
Chapter 1: Triangles and Circles
Solve the equation.
1. [latex]x-8 = 19 -2x[/latex]
2. [latex]2x-9 = 12 -x[/latex]
3. [latex]13x+5 = 2x -28[/latex]
4. [latex]4+9x = -7+x[/latex]
Solve the system
5. [latex]5x - 2y = -13, 2x+3y = -9[/latex]
6. [latex]4x+3y=9, 3x+2y= 8[/latex]
Historically, trigonometry began as the study of triangles and their properties. Let's review some definitions and facts from geometry.
If you tear off the corners of any triangle and line them up, as shown below, they will always form a straight angle.
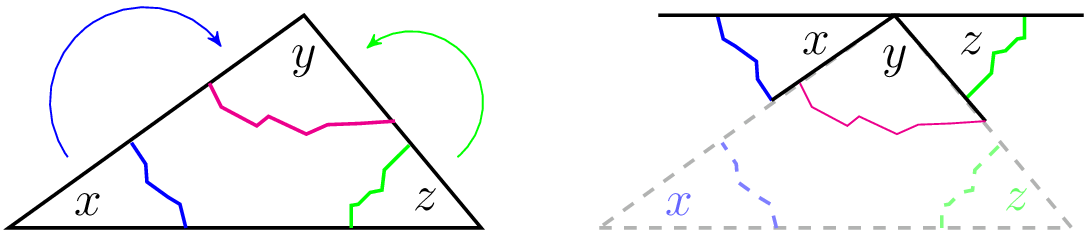
The sum of the angles in a triangle is [latex]180^{\circ}[/latex].
Two of the angles in the triangle at right are [latex]25^{\circ}[/latex] and [latex]115^{\circ}[/latex]. Find the third angle.
To find the third angle, we write an equation:
[latex]\begin{align*} x+25+115 = & 180 & \text{Simplify the left side.} \\ x+140 = & 180 & \text{Subtract 140 from both sides} \\ x= 40 \end{align*}[/latex]
The third angle is [latex]40^{\circ}[/latex]
Find each of the angles in the triangle at right.
[latex]x=39^{\circ}[/latex], [latex]2x=78[/latex], [latex]2x-15=63[/latex]. [latex]x=40^{\circ}[/latex]
Some special categories of triangles are particularly useful. Most important of these are the right triangles.
A right triangle has one angle of [latex]90^{\circ}[/latex]
The sum of the two smaller angles in a right triangle is [latex]90^{\circ}[/latex]. So
[latex]\begin{align*} x+34 = & 90 & \text{Subtract 34 from both sides.} \\ x =56 \end{align*}[/latex]
The unknown angle must be [latex]56^{\circ}[/latex]
No
An equilateral triangle has all three sides the same length.
The triangle is equilateral, so all of its angles are equal. Thus
[latex]\begin{align*} 3x= & 180 & \text{Divide both sides by 3}.\\ x = 60 \end{align*}[/latex]
Each of the angles is [latex]60^{\circ}[/latex]
Find [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex] in the triangle at right.
[latex]x=60^{\circ}[/latex],[latex]y=8[/latex],[latex]z=8[/latex]
An isosceles triangle has two sides of equal length. The angle between the equal sides is the vertex angle. The other two angles are the base angles.
Find [latex]x[/latex] and [latex]y[/latex] in the triangle at right.
The triangle is isosceles, so the base angles are equal. Therefore, [latex]y=38^{\circ}[/latex]. To find the vertex angle, we solve
[latex]\begin{align*} x+38+38=180 \\ x+76= & 180 & \text{Subtract 76 from both sides.}\\ x=104 \end{align*}[/latex]
The vertex angle is [latex]104^{\circ}[/latex]
Find [latex]x[/latex] and [latex]y[/latex] in the figure at right.
[latex]x=140^{\circ},~y=9[/latex]
In addition to the facts about triangles reviewed above, there are several useful properties of angles.
In the figure at right,
In trigonometry we often use lowercase Greek letters to represent unknown angles (or, more specifically, the measure of the angle in degrees).
| Greek Alphabet | ||
| [latex]\alpha[/latex](alpha) | [latex]\beta[/latex](beta) | [latex]\gamma[/latex](gamma) |
| [latex]\delta[/latex](delta) | [latex]\epsilon[/latex](epsilon) | [latex]\zeta[/latex](zeta) |
| [latex]\eta[/latex](eta) | [latex]\theta[/latex](theta) | [latex]\iota[/latex](iota) |
| [latex]\kappa[/latex](kappa) | [latex]\lambda[/latex](lambda) | [latex]\mu[/latex](mu) |
| [latex]\nu[/latex](nu) | [latex]\xi[/latex](xi) | [latex]\omicron[/latex](omicron) |
| [latex]\pi[/latex](pi) | [latex]\rho[/latex](rho) | [latex]\sigma[/latex](sigma) |
| [latex]\tau[/latex](tau) | [latex]\upsilon[/latex](upsilon) | [latex]\phi[/latex](phi) |
| [latex]\chi[/latex](chi) | [latex]\psi[/latex](psi) | [latex]\omega[/latex](omega) |
In the next exercise, we use the Greek letters [latex]\alpha[/latex] (alpha), [latex]\beta[/latex] (beta), and [latex]\gamma[/latex] (gamma).
In the figure, [latex]\alpha[/latex],[latex]\beta[/latex], and [latex]\gamma[/latex] denote the measures of the angles in degrees.
[latex]\alpha=130^{\circ},~\beta=50^{\circ}, ~\gamma=130^{\circ}[/latex]. The non-adjacent angles are equal.
Non-adjacent angles formed by the intersection of two straight lines are called vertical angles. In the previous exercise, the angles labeled [latex]\alpha[/latex] and [latex]\gamma[/latex]are vertical angles, as are the angles labeled [latex]\beta[/latex] and [latex]50^{\circ}[/latex].
Explain why [latex]\alpha=\beta[/latex] in the triangle at right.
Because they are the base angles of an isosceles triangle, [latex]\theta[/latex](theta) and [latex]\phi[/latex](phi) are equal. Also,[latex]\alpha=\theta[/latex] because they are vertical angles, and similarly [latex]\beta=\phi[/latex]. Therefore,[latex]\alpha=\beta[/latex] because they are equal to equal quantities.
Find all the unknown angles in the figure at right. (You will find a list of all the Greek letters and their names prior to Checkpoint 1.10.)
[latex]\alpha=40^{\circ},~\beta=140^{\circ},~\gamma=75^{\circ},~\delta=65^{\circ}[/latex]
If parallel lines are intersected by a transversal, the alternate interior angles are equal. Corresponding angles are also equal.
The parallelogram ABCD shown at right is formed by the intersection of two sets of parallel lines. Show that the opposite angles of the parallelogram are equal.
Angles [latex]1[/latex] and [latex]2[/latex] are equal because they are alternate interior angles, and angles [latex]2[/latex] and [latex]3[/latex] are equal because they are corresponding angles. Therefore angles [latex]1[/latex] and [latex]3[/latex], the opposite angles of the parallelogram, are equal. Similarly, you can show that angles [latex]4[/latex], [latex]5[/latex], and [latex]6[/latex] are equal.
Show that the adjacent angles of a parallelogram are supplementary. (You can use angles [latex]1[/latex] and [latex]4[/latex] in the parallelogram of the previous example.)
Note that angles [latex]2[/latex] and [latex]6[/latex] are supplementary because they form a straight angle. Angle [latex]1[/latex] equals angle [latex]2[/latex] because they are alternate interior angles, and similarly angle [latex]4[/latex] equals angle [latex]5[/latex]. Angle [latex]5[/latex] equals angle [latex]6[/latex] because they are corresponding angles. Thus, angle [latex]4[/latex] equals angle [latex]6[/latex], and angle [latex]1[/latex] equals angle [latex]2[/latex]. So angles [latex]4[/latex] and [latex]1[/latex] are supplementary because [latex]2[/latex] and [latex]6[/latex] are.
In the Section 1.1 Summary, you will find a list of vocabulary words and a summary of the facts from geometry that we reviewed in this section. You will also find a set of study questions to test your understanding and a list of skills to practice in the homework problems.
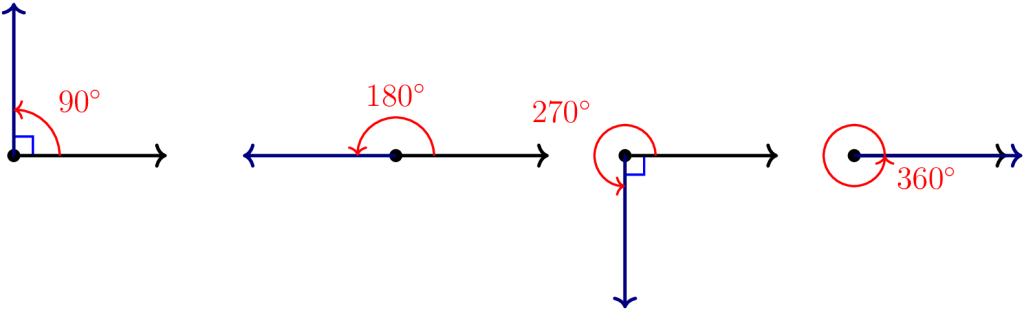
A straight angle is a type of angle that measures exactly 180 degrees. It is formed when two opposite rays or line segments extend from the same point and create a straight line.
A right angle is a type of angle that measures exactly 90 degrees. It is formed when two lines or line segments intersect each other perpendicularly, meaning that they meet at a 90-degree angle.
A right triangle is a type of triangle that has one interior angle measuring exactly 90 degrees, or a “right angle.”
An equilateral triangle is a type of triangle in which all three sides are equal in length, and all three angles are also equal, measuring 60 degrees each.
An isosceles triangle is a type of triangle that has two sides of equal length and two equal angles opposite those sides.
Vertex angle is defined as the angle formed by two lines or rays that intersect at a point. These two rays make the sides of the angle. In other words, the angle associated within a given vertex is called vertex angle.
A base angle of a shape is an angle within a shape that contains the base of the shape as one of its sides.
Two angles are considered supplementary if the sum of their measures is exactly 180 degrees.
Two angles are considered complementary if the sum of their measures is exactly 90 degrees.
An acute angle is a type of angle that measures greater than 0 degrees but less than 90 degrees, meaning that it is smaller than a right angle.
An obtuse angle is a type of angle that measures greater than 90 degrees but less than 180 degrees, meaning that it is larger than a right angle.
Vertical angles are a pair of non-adjacent angles that are opposite each other, formed by the intersection of two lines or line segments, and are always congruent, meaning that they have the same measure.
Corresponding angles are a pair of angles that are formed by a transversal intersecting two parallel lines, located in corresponding positions in relation to the transversal, and are congruent, meaning that they have the same measure.
Alternate interior angles are a pair of angles that are formed by a transversal intersecting two parallel lines, located on opposite sides of the transversal and in between the two parallel lines, and are congruent, meaning that they have the same measure.
A parallelogram is a quadrilateral with two pairs of parallel sides, where opposite sides are congruent (have the same length) and opposite angles are also congruent (have the same measure).
A transversal is a line that intersects two or more other lines or line segments at different points, forming eight angles, four of which are congruent pairs of vertical angles.