Introduction

Musical instruments produce sound by the vibration of a string on a violin, guitar, or piano, or a column of air in a brass or woodwind instrument. The vibration causes a periodic variation in air pressure that is heard as sound. Periodic vibrations create a pleasing, musical sound, while random vibrations sound like noise (Figure 1).

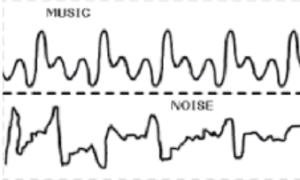
There are three distinguishing characteristics of musical notes: loudness, pitch, and timbre.

• The loudness of a note is measured by the magnitude, or amplitude, of the changes in air pressure.
• The pitch of the note is determined by its frequency, the number of times its basic pattern is repeated each second. For example, a note with pitch 440 hertz repeats its pattern 440 times per second. Humans can hear frequencies that range roughly from 20 to 18,000 hertz.
• The timbre of the note allows us to tell a piano note from a guitar note with the same loudness and pitch.

The simplest pressure vibration is produced by a tuning fork. The graph of its pressure function resembles a sine curve, and the corresponding sound is called a pure tone. When a musical instrument produces a pure tone, not only is its frequency produced, but integer multiples of the fundamental frequency, called harmonics, are produced as well (Figure 2). Sine curves of different frequencies combine to create the timbre of the note.

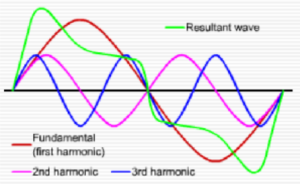
If two musical instruments play the same note, the notes have the same pitch, but they sound different because the amplitudes of each of the harmonics is different for the two instruments (Figure 3).

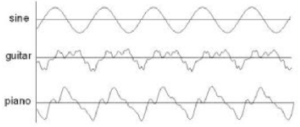
The French mathematician Joseph Fourier, who lived from 1768 to 1830, discovered that any periodic wave can be written as the sum of a number of sines and cosines with differing amplitudes (Figure 4).

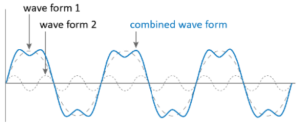
Fourier created a method for determining the frequencies and amplitudes of the simpler waves that make up a more complicated periodic function. Applying the Fourier transform to a sampled musical note reveals which component frequencies are present in the note. The same sound can then be re-synthesized by including those frequency components (Figure 5).

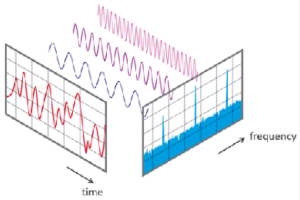
Today, Fourier analysis is the foundation of signal processing, not only for audio waves, but for radio waves, light waves, seismic waves, and even images. By analyzing a compound waveform, the “noise” components can be isolated and removed in order to smooth out the signal. Fourier analysis is also used in X-ray crystallography to reconstruct a crystal structure from its diffraction pattern, and in nuclear magnetic resonance spectroscopy to determine the mass of ions from the frequency of their motion in a magnetic field.

Class Activities