161 Equilibrium Calculations
Paul Flowers; Edward J. Neth; William R. Robinson; Klaus Theopold; and Richard Langley
[latexpage]
Learning Objectives
By the end of this section, you will be able to:
- Identify the changes in concentration or pressure that occur for chemical species in equilibrium systems
- Calculate equilibrium concentrations or pressures and equilibrium constants, using various algebraic approaches
- Explain how temperature affects the spontaneity of some proceses
- Relate standard free energy changes to equilibrium constants
Having covered the essential concepts of chemical equilibria in the preceding sections of this chapter, this final section will demonstrate the more practical aspect of using these concepts and appropriate mathematical strategies to perform various equilibrium calculations. These types of computations are essential to many areas of science and technology—for example, in the formulation and dosing of pharmaceutical products. After a drug is ingested or injected, it is typically involved in several chemical equilibria that affect its ultimate concentration in the body system of interest. Knowledge of the quantitative aspects of these equilibria is required to compute a dosage amount that will solicit the desired therapeutic effect.
Many of the useful equilibrium calculations that will be demonstrated here require terms representing changes in reactant and product concentrations. These terms are derived from the stoichiometry of the reaction, as illustrated by decomposition of ammonia:
As shown earlier in this chapter, this equilibrium may be established within a sealed container that initially contains either NH3 only, or a mixture of any two of the three chemical species involved in the equilibrium. Regardless of its initial composition, a reaction mixture will show the same relationships between changes in the concentrations of the three species involved, as dictated by the reaction stoichiometry (see also the related content on expressing reaction rates in the chapter on kinetics). For example, if the nitrogen concentration increases by an amount x:
the corresponding changes in the other species concentrations are
where the negative sign indicates a decrease in concentration.
Determining Relative Changes in Concentration Derive the missing terms representing concentration changes for each of the following reactions.
(a) \(\begin{array}{cccc}{\text{C}}_{2}{\text{H}}_{2}\left(g\right)+\hfill & 2{\text{Br}}_{2}\left(g\right)\hfill & ⇌\hfill & {\text{C}}_{2}{\text{H}}_{2}{\text{Br}}_{4}\left(g\right)\hfill \\ x\hfill & _____\hfill & & _____\hfill \end{array}\)
(b) \(\begin{array}{cccc}{\text{I}}_{2}\left(aq\right)+\hfill & {\text{I}}^{\text{−}}\left(aq\right)\hfill & ⇌\hfill & {\text{I}}_{3}{}^{\text{−}}\left(aq\right)\hfill \\ _____\hfill & _____\hfill & & x\hfill \end{array}\)
(c) \(\begin{array}{ccccc}{\text{C}}_{3}{\text{H}}_{8}\left(g\right)+\hfill & 5{\text{O}}_{2}\left(g\right)\hfill & ⇌\hfill & 3{\text{CO}}_{2}\left(g\right)+\hfill & 4{\text{H}}_{2}\text{O}\left(g\right)\hfill \\ x\hfill & _____\hfill & & _____\hfill & _____\hfill \end{array}\)
Solution (a) \(\begin{array}{cccc}{\text{C}}_{2}{\text{H}}_{2}\left(g\right)+\hfill & 2{\text{Br}}_{2}\left(g\right)\hfill & ⇌\hfill & {\text{C}}_{2}{\text{H}}_{2}{\text{Br}}_{4}\left(g\right)\hfill \\ x\hfill & 2x\hfill & & -x\hfill \end{array}\)
(b) \(\begin{array}{cccc}{\text{I}}_{2}\left(aq\right)+\hfill & {\text{I}}^{\text{−}}\left(aq\right)\hfill & ⇌\hfill & {\text{I}}_{3}{}^{\text{−}}\left(aq\right)\hfill \\ -x\hfill & -x\hfill & & x\hfill \end{array}\)
(c) \(\begin{array}{lllll}{\text{C}}_{3}{\text{H}}_{8}\left(g\right)+\hfill & 5{\text{O}}_{2}\left(g\right)\hfill & ⇌\hfill & 3{\text{CO}}_{2}\left(g\right)+\hfill & 4{\text{H}}_{2}\text{O}\left(g\right)\hfill \\ x\hfill & 5x\hfill & & -3x\hfill & -4x\hfill \end{array}\)
Check Your Learning Complete the changes in concentrations for each of the following reactions:
(a) \(\begin{array}{llll}2{\text{SO}}_{2}\left(g\right)+\hfill & {\text{O}}_{2}\left(g\right)\hfill & ⇌\hfill & 2{\text{SO}}_{3}\left(g\right)\hfill \\ _____\hfill & x\hfill & & _____\hfill \end{array}\)
(b) \(\begin{array}{lll}{\text{C}}_{4}{\text{H}}_{8}\left(g\right)\hfill & ⇌\hfill & 2{\text{C}}_{2}{\text{H}}_{4}\left(g\right)\hfill \\ _____\hfill & & -2x\hfill \end{array}\)
(c) \(\begin{array}{lllll}4{\text{NH}}_{3}\left(g\right)+\hfill & 7{\text{H}}_{2}\text{O}\left(g\right)\hfill & ⇌\hfill & 4{\text{NO}}_{2}\left(g\right)+\hfill & 6{\text{H}}_{2}\text{O}\left(g\right)\hfill \\ \\ _____\hfill & _____\hfill & & _____\hfill & _____\hfill \end{array}\)
(a) 2x, x, −2x; (b) x, −2x; (c) 4x, 7x, −4x, −6x or −4x, −7x, 4x, 6x
Calculation of an Equilibrium Constant
The equilibrium constant for a reaction is calculated from the equilibrium concentrations (or pressures) of its reactants and products. If these concentrations are known, the calculation simply involves their substitution into the K expression, as was illustrated by (Figure). A slightly more challenging example is provided next, in which the reaction stoichiometry is used to derive equilibrium concentrations from the information provided. The basic strategy of this computation is helpful for many types of equilibrium computations and relies on the use of terms for the reactant and product concentrations initially present, for how they change as the reaction proceeds, and for what they are when the system reaches equilibrium. The acronym ICE is commonly used to refer to this mathematical approach, and the concentrations terms are usually gathered in a tabular format called an ICE table.
Calculation of an Equilibrium Constant Iodine molecules react reversibly with iodide ions to produce triiodide ions.
If a solution with the concentrations of I2 and I− both equal to 1.000 \(×\) 10−3M before reaction gives an equilibrium concentration of I2 of 6.61 \(×\) 10−4M, what is the equilibrium constant for the reaction?
Solution To calculate the equilibrium constants, equilibrium concentrations are needed for all the reactants and products:
Provided are the initial concentrations of the reactants and the equilibrium concentration of the product. Use this information to derive terms for the equilibrium concentrations of the reactants, presenting all the information in an ICE table.
![This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ), Change ( M ), Equilibrium concentration ( M ). The second column has the header, “I subscript 2 plus sign I superscript negative sign equilibrium arrow I subscript 3 superscript negative sign.” Under the second column is a subgroup of three rows and three columns. The first column has the following: 1.000 times 10 to the negative third power, negative x, [ I subscript 2 ] subscript i minus x. The second column has the following: 1.000 times 10 to the negative third power, negative x, [ I superscript negative sign ] subscript i minus x. The third column has the following: 0, positive x, [ I superscript negative sign ] subscript i plus x.](https://louis.pressbooks.pub/app/uploads/sites/2/2019/07/CNX_Chem_13_04_ICETable1_img.jpg)
At equilibrium the concentration of I2 is 6.61 \(×\) 10−4M so that
The ICE table may now be updated with numerical values for all its concentrations:

Finally, substitute the equilibrium concentrations into the K expression and solve:
Check Your Learning Ethanol and acetic acid react and form water and ethyl acetate, the solvent responsible for the odor of some nail polish removers.
When 1 mol each of C2H5OH and CH3CO2H are allowed to react in 1 L of the solvent dioxane, equilibrium is established when \(\frac{1}{3}\) mol of each of the reactants remains. Calculate the equilibrium constant for the reaction. (Note: Water is a solute in this reaction.)
Kc = 4
Calculation of a Missing Equilibrium Concentration
When the equilibrium constant and all but one equilibrium concentration are provided, the other equilibrium concentration(s) may be calculated. A computation of this sort is illustrated in the next example exercise.
Calculation of a Missing Equilibrium ConcentrationNitrogen oxides are air pollutants produced by the reaction of nitrogen and oxygen at high temperatures. At 2000 °C, the value of the Kc for the reaction, \({\text{N}}_{2}\left(g\right)+{\text{O}}_{2}\left(g\right)⇌2\text{NO}\left(g\right),\) is 4.1 \(×\) 10−4. Calculate the equilibrium concentration of NO(g) in air at 1 atm pressure and 2000 °C. The equilibrium concentrations of N2 and O2 at this pressure and temperature are 0.036 M and 0.0089 M, respectively.
Solution Substitute the provided quantities into the equilibrium constant expression and solve for [NO]:
Thus [NO] is 3.6 \(×\) 10−4 mol/L at equilibrium under these conditions.
To confirm this result, it may be used along with the provided equilibrium concentrations to calculate a value for K:
This result is consistent with the provided value for K within nominal uncertainty, differing by just 1 in the least significant digit’s place.
Check Your Learning The equilibrium constant Kc for the reaction of nitrogen and hydrogen to produce ammonia at a certain temperature is 6.00 \(×\) 10−2. Calculate the equilibrium concentration of ammonia if the equilibrium concentrations of nitrogen and hydrogen are 4.26 M and 2.09 M, respectively.
1.53 mol/L
Calculation of Equilibrium Concentrations from Initial Concentrations
Perhaps the most challenging type of equilibrium calculation can be one in which equilibrium concentrations are derived from initial concentrations and an equilibrium constant. For these calculations, a four-step approach is typically useful:
- Identify the direction in which the reaction will proceed to reach equilibrium.
- Develop an ICE table.
- Calculate the concentration changes and, subsequently, the equilibrium concentrations.
- Confirm the calculated equilibrium concentrations.
The last two example exercises of this chapter demonstrate the application of this strategy.
Calculation of Equilibrium Concentrations Under certain conditions, the equilibrium constant Kc for the decomposition of PCl5(g) into PCl3(g) and Cl2(g) is 0.0211. What are the equilibrium concentrations of PCl5, PCl3, and Cl2 in a mixture that initially contained only PCl5 at a concentration of 1.00 M?
Solution Use the stepwise process described earlier.
-
Determine the direction the reaction proceeds.
The balanced equation for the decomposition of PCl5 is
\({\text{PCl}}_{5}\left(g\right)⇌{\text{PCl}}_{3}\left(g\right)+{\text{Cl}}_{2}\left(g\right)\)Because only the reactant is present initially Qc = 0 and the reaction will proceed to the right.
-
Develop an ICE table.
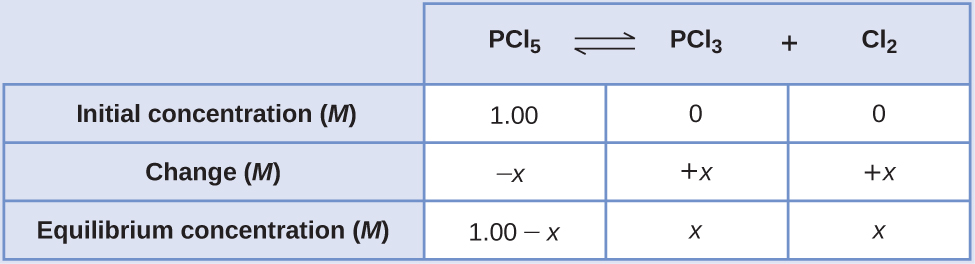
-
Solve for the change and the equilibrium concentrations.
Substituting the equilibrium concentrations into the equilibrium constant equation gives
\({K}_{c}=\phantom{\rule{0.2em}{0ex}}\frac{\left[{\text{PCl}}_{3}\right]\left[{\text{Cl}}_{2}\right]}{\left[{\text{PCl}}_{5}\right]}\phantom{\rule{0.2em}{0ex}}=0.0211\)\(=\phantom{\rule{0.2em}{0ex}}\frac{\left(x\right)\left(x\right)}{\left(1.00-x\right)}\)\(0.0211=\phantom{\rule{0.2em}{0ex}}\frac{\left(x\right)\left(x\right)}{\left(1.00-x\right)}\)\(0.0211\left(1.00-x\right)={x}^{2}\)\({x}^{2}+0.0211x-0.0211=0\)Appendix B shows an equation of the form ax2 + bx + c = 0 can be rearranged to solve for x:
\(x=\phantom{\rule{0.2em}{0ex}}\frac{-b\phantom{\rule{0.2em}{0ex}}±\phantom{\rule{0.2em}{0ex}}\sqrt{{b}^{2}-4ac}}{2a}\)In this case, a = 1, b = 0.0211, and c = −0.0211. Substituting the appropriate values for a, b, and c yields:
\(x=\phantom{\rule{0.2em}{0ex}}\frac{-0.0211\phantom{\rule{0.2em}{0ex}}±\phantom{\rule{0.2em}{0ex}}\sqrt{{\left(0.0211\right)}^{2}-4\left(1\right)\left(-0.0211\right)}}{2\left(1\right)}\)\(=\phantom{\rule{0.2em}{0ex}}\frac{-0.0211\phantom{\rule{0.2em}{0ex}}±\phantom{\rule{0.2em}{0ex}}\sqrt{\left(4.45\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\right)+\left(8.44\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}\right)}}{2}\)\(=\phantom{\rule{0.2em}{0ex}}\frac{-0.0211\phantom{\rule{0.2em}{0ex}}±\phantom{\rule{0.2em}{0ex}}0.291}{2}\)The two roots of the quadratic are, therefore,
\(x=\phantom{\rule{0.2em}{0ex}}\frac{-0.0211+0.291}{2}\phantom{\rule{0.2em}{0ex}}=0.135\)and
\(x=\phantom{\rule{0.2em}{0ex}}\frac{-0.0211-0.291}{2}\phantom{\rule{0.2em}{0ex}}=-0.156\)For this scenario, only the positive root is physically meaningful (concentrations are either zero or positive), and so x = 0.135 M.
The equilibrium concentrations are
\(\left[{\text{PCl}}_{5}\right]\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}1.00-0.135=0.87\phantom{\rule{0.2em}{0ex}}M\)\(\left[{\text{PCl}}_{3}\right]=x=0.135\phantom{\rule{0.2em}{0ex}}M\)\(\left[{\text{Cl}}_{2}\right]=x=0.135\phantom{\rule{0.2em}{0ex}}M\) -
Confirm the calculated equilibrium concentrations.
Substitution into the expression for Kc (to check the calculation) gives
\({K}_{c}=\phantom{\rule{0.2em}{0ex}}\frac{\left[{\text{PCl}}_{3}\right]\left[{\text{Cl}}_{2}\right]}{\left[{\text{PCl}}_{5}\right]}=\phantom{\rule{0.2em}{0ex}}\frac{\left(0.135\right)\left(0.135\right)}{0.87}\phantom{\rule{0.2em}{0ex}}=0.021\)The equilibrium constant calculated from the equilibrium concentrations is equal to the value of Kc given in the problem (when rounded to the proper number of significant figures).
Check Your Learning Acetic acid, CH3CO2H, reacts with ethanol, C2H5OH, to form water and ethyl acetate, CH3CO2C2H5.
The equilibrium constant for this reaction with dioxane as a solvent is 4.0. What are the equilibrium concentrations for a mixture that is initially 0.15 M in CH3CO2H, 0.15 M in C2H5OH, 0.40 M in CH3CO2C2H5, and 0.40 M in H2O?
[CH3CO2H] = 0.36 M, [C2H5OH] = 0.36 M, [CH3CO2C2H5] = 0.17 M, [H2O] = 0.17 M
Check Your Learning A 1.00-L flask is filled with 1.00 moles of H2 and 2.00 moles of I2. The value of the equilibrium constant for the reaction of hydrogen and iodine reacting to form hydrogen iodide is 50.5 under the given conditions. What are the equilibrium concentrations of H2, I2, and HI in moles/L?
[H2] = 0.06 M, [I2] = 1.06 M, [HI] = 1.88 M
Calculation of Equilibrium Concentrations Using an Algebra-Simplifying Assumption What are the concentrations at equilibrium of a 0.15 M solution of HCN?
Solution Using “x” to represent the concentration of each product at equilibrium gives this ICE table.
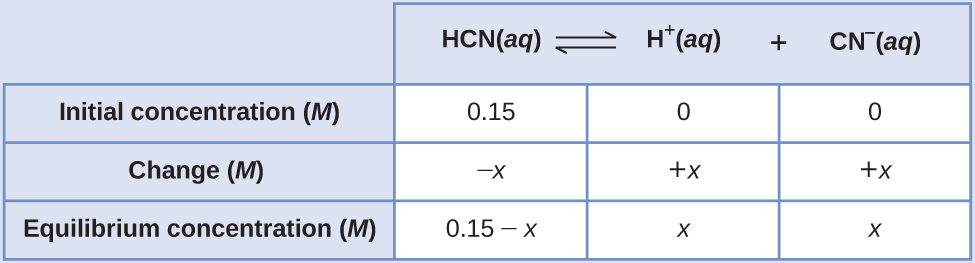
Substitute the equilibrium concentration terms into the Kc expression
Rearrange to the quadratic form and solve for x
Thus [H+] = [CN–] = x = 8.6 \(×\) 10–6M and [HCN] = 0.15 – x = 0.15 M.
Note in this case that the change in concentration is significantly less than the initial concentration (a consequence of the small K), and so the initial concentration experiences a negligible change:
This approximation allows for a more expedient mathematical approach to the calculation that avoids the need to solve for the roots of a quadratic equation:
The value of x calculated is, indeed, much less than the initial concentration
and so the approximation was justified. If this simplified approach were to yield a value for x that did not justify the approximation, the calculation would need to be repeated without making the approximation.
Check Your Learning What are the equilibrium concentrations in a 0.25 M NH3 solution?
\(\left[{\text{OH}}^{\text{−}}\right]=\left[{\text{NH}}_{4}{}^{\text{+}}\right]=0.0021\phantom{\rule{0.2em}{0ex}}M;\) [NH3] = 0.25 M
Temperature Dependence of Spontaneity
As was previously demonstrated in the section on entropy in an earlier chapter, the spontaneity of a process may depend upon the temperature of the system. Phase transitions, for example, will proceed spontaneously in one direction or the other depending upon the temperature of the substance in question. Likewise, some chemical reactions can also exhibit temperature dependent spontaneities. To illustrate this concept, the equation relating free energy change to the enthalpy and entropy changes for the process is considered:
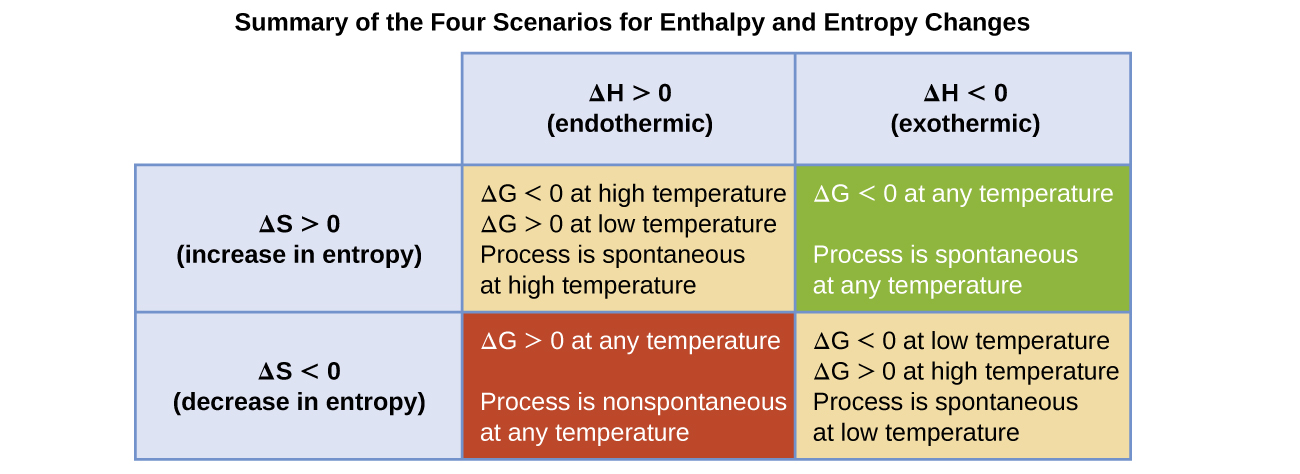
The spontaneity of a process, as reflected in the arithmetic sign of its free energy change, is then determined by the signs of the enthalpy and entropy changes and, in some cases, the absolute temperature. Since T is the absolute (kelvin) temperature, it can only have positive values. Four possibilities therefore exist with regard to the signs of the enthalpy and entropy changes:
- Both ΔH and ΔS are positive. This condition describes an endothermic process that involves an increase in system entropy. In this case, ΔG will be negative if the magnitude of the TΔS term is greater than ΔH. If the TΔS term is less than ΔH, the free energy change will be positive. Such a process is spontaneous at high temperatures and nonspontaneous at low temperatures.
- Both ΔH and ΔS are negative. This condition describes an exothermic process that involves a decrease in system entropy. In this case, ΔG will be negative if the magnitude of the TΔS term is less than ΔH. If the TΔS term’s magnitude is greater than ΔH, the free energy change will be positive. Such a process is spontaneous at low temperatures and nonspontaneous at high temperatures.
- ΔH is positive and ΔS is negative. This condition describes an endothermic process that involves a decrease in system entropy. In this case, ΔG will be positive regardless of the temperature. Such a process is nonspontaneous at all temperatures.
- ΔH is negative and ΔS is positive. This condition describes an exothermic process that involves an increase in system entropy. In this case, ΔG will be negative regardless of the temperature. Such a process is spontaneous at all temperatures.
These four scenarios are summarized in (Figure).
Predicting the Temperature Dependence of Spontaneity The incomplete combustion of carbon is described by the following equation:
How does the spontaneity of this process depend upon temperature?
Solution Combustion processes are exothermic (ΔH < 0). This particular reaction involves an increase in entropy due to the accompanying increase in the amount of gaseous species (net gain of one mole of gas, ΔS > 0). The reaction is therefore spontaneous (ΔG < 0) at all temperatures.
Check Your Learning Popular chemical hand warmers generate heat by the air-oxidation of iron:
How does the spontaneity of this process depend upon temperature?
ΔH and ΔS are negative; the reaction is spontaneous at low temperatures.
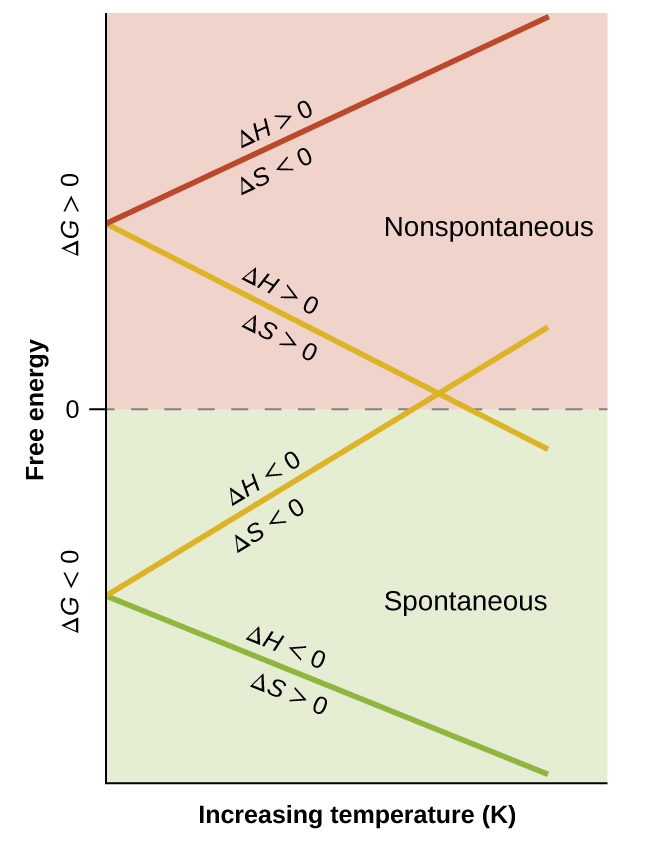
When considering the conclusions drawn regarding the temperature dependence of spontaneity, it is important to keep in mind what the terms “high” and “low” mean. Since these terms are adjectives, the temperatures in question are deemed high or low relative to some reference temperature. A process that is nonspontaneous at one temperature but spontaneous at another will necessarily undergo a change in “spontaneity” (as reflected by its ΔG) as temperature varies. This is clearly illustrated by a graphical presentation of the free energy change equation, in which ΔG is plotted on the y axis versus T on the x axis:
Such a plot is shown in (Figure). A process whose enthalpy and entropy changes are of the same arithmetic sign will exhibit a temperature-dependent spontaneity as depicted by the two yellow lines in the plot. Each line crosses from one spontaneity domain (positive or negative ΔG) to the other at a temperature that is characteristic of the process in question. This temperature is represented by the x-intercept of the line, that is, the value of T for which ΔG is zero:
So, saying a process is spontaneous at “high” or “low” temperatures means the temperature is above or below, respectively, that temperature at which ΔG for the process is zero. As noted earlier, the condition of ΔG = 0 describes a system at equilibrium.
Equilibrium Temperature for a Phase TransitionAs defined in the chapter on liquids and solids, the boiling point of a liquid is the temperature at which its liquid and gaseous phases are in equilibrium (that is, when vaporization and condensation occur at equal rates). Use the information in Appendix G to estimate the boiling point of water.
Solution The process of interest is the following phase change:
When this process is at equilibrium, ΔG = 0, so the following is true:
Using the standard thermodynamic data from Appendix G,
The accepted value for water’s normal boiling point is 373.2 K (100.0 °C), and so this calculation is in reasonable agreement. Note that the values for enthalpy and entropy changes data used were derived from standard data at 298 K (Appendix G). If desired, you could obtain more accurate results by using enthalpy and entropy changes determined at (or at least closer to) the actual boiling point.
Check Your Learning Use the information in Appendix G to estimate the boiling point of CS2.
313 K (accepted value 319 K)
Free Energy and Equilibrium
The free energy change for a process may be viewed as a measure of its driving force. A negative value for ΔG represents a driving force for the process in the forward direction, while a positive value represents a driving force for the process in the reverse direction. When ΔG is zero, the forward and reverse driving forces are equal, and the process occurs in both directions at the same rate (the system is at equilibrium).
In the section on equilibrium, the reaction quotient, Q, was introduced as a convenient measure of the status of an equilibrium system. Recall that Q is the numerical value of the mass action expression for the system, and that you may use its value to identify the direction in which a reaction will proceed in order to achieve equilibrium. When Q is lesser than the equilibrium constant, K, the reaction will proceed in the forward direction until equilibrium is reached and Q = K. Conversely, if Q > K, the process will proceed in the reverse direction until equilibrium is achieved.
The free energy change for a process taking place with reactants and products present under nonstandard conditions (pressures other than 1 bar; concentrations other than 1 M) is related to the standard free energy change, according to this equation:
R is the gas constant (8.314 J/K mol), T is the kelvin or absolute temperature, and Q is the reaction quotient. This equation may be used to predict the spontaneity for a process under any given set of conditions as illustrated in (Figure).
Calculating ΔG under Nonstandard Conditions What is the free energy change for the process shown here under the specified conditions?
T = 25 °C, \({P}_{{\text{N}}_{2}}=\text{0.870 atm},\) \({P}_{{\text{H}}_{2}}=\text{0.250 atm},\) and \({P}_{{\text{NH}}_{3}}=\text{12.9 atm}\)
Solution The equation relating free energy change to standard free energy change and reaction quotient may be used directly:
Since the computed value for ΔG is positive, the reaction is nonspontaneous under these conditions.
Check Your Learning Calculate the free energy change for this same reaction at 875 °C in a 5.00 L mixture containing 0.100 mol of each gas. Is the reaction spontaneous under these conditions?
ΔG = −47 kJ/mol; yes
For a system at equilibrium, Q = K and ΔG = 0, and the previous equation may be written as
This form of the equation provides a useful link between these two essential thermodynamic properties, and it can be used to derive equilibrium constants from standard free energy changes and vice versa. The relations between standard free energy changes and equilibrium constants are summarized in (Figure).
| Relations between Standard Free Energy Changes and Equilibrium Constants | ||
|---|---|---|
| K | ΔG° | Composition of an Equilibrium Mixture |
| > 1 | < 0 | Products are more abundant |
| < 1 | > 0 | Reactants are more abundant |
| = 1 | = 0 | Reactants and products are comparably abundant |
Calculating an Equilibrium Constant using Standard Free Energy Change Given that the standard free energies of formation of Ag+(aq), Cl−(aq), and AgCl(s) are 77.1 kJ/mol, −131.2 kJ/mol, and −109.8 kJ/mol, respectively, calculate the solubility product, Ksp, for AgCl.
Solution The reaction of interest is the following:
The standard free energy change for this reaction is first computed using standard free energies of formation for its reactants and products:
The equilibrium constant for the reaction may then be derived from its standard free energy change:
This result is in reasonable agreement with the value provided in Appendix J.
Check Your Learning Use the thermodynamic data provided in Appendix G to calculate the equilibrium constant for the dissociation of dinitrogen tetroxide at 25 °C.
K = 6.9
To further illustrate the relation between these two essential thermodynamic concepts, consider the observation that reactions spontaneously proceed in a direction that ultimately establishes equilibrium. As may be shown by plotting the free energy change versus the extent of the reaction (for example, as reflected in the value of Q), equilibrium is established when the system’s free energy is minimized ((Figure)). If a system consists of reactants and products in nonequilibrium amounts (Q ≠ K), the reaction will proceed spontaneously in the direction necessary to establish equilibrium.
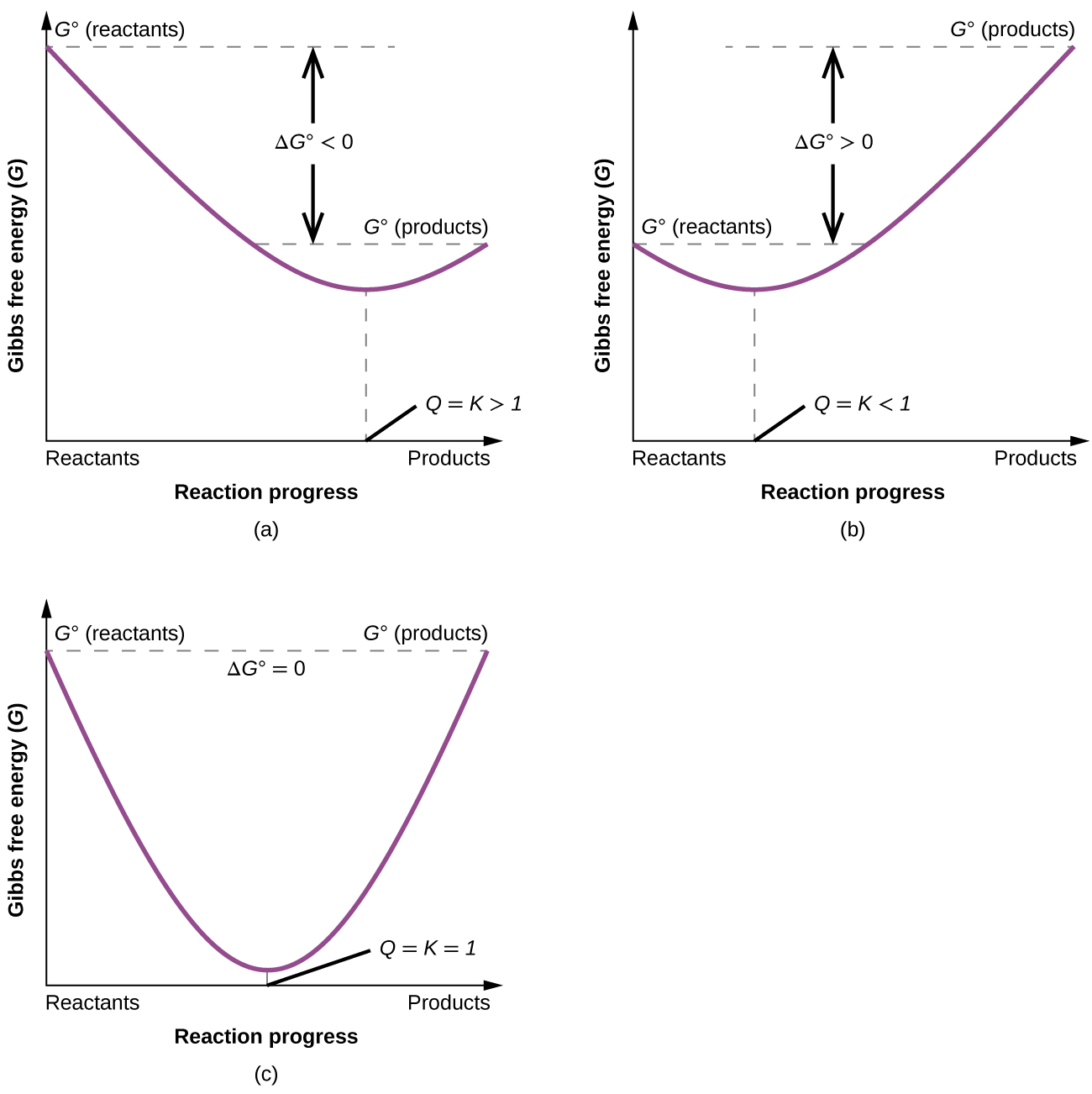
Key Concepts and Summary
Calculating values for equilibrium constants and/or equilibrium concentrations is of practical benefit to many applications. A mathematical strategy that uses initial concentrations, changes in concentrations, and equilibrium concentrations (and goes by the acronym ICE) is useful for several types of equilibrium calculations. We also learned that a negative value for ΔG indicates a spontaneous process; a positive ΔG indicates a nonspontaneous process; and a ΔG of zero indicates that the system is at equilibrium. We also saw how free energy, spontaneity, and equilibrium relate.
Chemistry End of Chapter Exercises
A reaction is represented by this equation: \(\text{A}\left(aq\right)+2\text{B}\left(aq\right)⇌2\text{C}\left(aq\right)\phantom{\rule{5em}{0ex}}{K}_{c}=1\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\)
(a) Write the mathematical expression for the equilibrium constant.
(b) Using concentrations ≤1 M, identify two sets of concentrations that describe a mixture of A, B, and C at equilibrium.
\({K}_{c}=\phantom{\rule{0.2em}{0ex}}\frac{{\left[\text{C}\right]}^{2}}{\left[\text{A}\right]{\left[\text{B}\right]}^{2}}.\) [A] = 0.1 M, [B] = 0.1 M, [C] = 1 M; and [A] = 0.01, [B] = 0.250, [C] = 0.791.
A reaction is represented by this equation: \(2\text{W}\left(aq\right)⇌\text{X}\left(aq\right)+2\text{Y}\left(aq\right)\phantom{\rule{5em}{0ex}}{K}_{c}=5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\)
(a) Write the mathematical expression for the equilibrium constant.
(b) Using concentrations of ≤1 M, identify two sets of concentrations that describe a mixture of W, X, and Y at equilibrium.
What is the value of the equilibrium constant at 500 °C for the formation of NH3 according to the following equation?
\({\text{N}}_{2}\left(g\right)+3{\text{H}}_{2}\left(g\right)⇌2{\text{NH}}_{3}\left(g\right)\)
An equilibrium mixture of NH3(g), H2(g), and N2(g) at 500 °C was found to contain 1.35 M H2, 1.15 M N2, and 4.12 \(×\) 10−1M NH3.
Kc = 6.00 \(×\) 10−2
Hydrogen is prepared commercially by the reaction of methane and water vapor at elevated temperatures.
\({\text{CH}}_{4}\left(g\right)+{\text{H}}_{2}\text{O}\left(g\right)⇌3{\text{H}}_{2}\left(g\right)+\text{CO}\left(g\right)\)
What is the equilibrium constant for the reaction if a mixture at equilibrium contains gases with the following concentrations: CH4, 0.126 M; H2O, 0.242 M; CO, 0.126 M; H2 1.15 M, at a temperature of 760 °C?
A 0.72-mol sample of PCl5 is put into a 1.00-L vessel and heated. At equilibrium, the vessel contains 0.40 mol of PCl3(g) and 0.40 mol of Cl2(g). Calculate the value of the equilibrium constant for the decomposition of PCl5 to PCl3 and Cl2 at this temperature.
Kc = 0.50
At 1 atm and 25 °C, NO2 with an initial concentration of 1.00 M is 0.0033% decomposed into NO and O2. Calculate the value of the equilibrium constant for the reaction.
\(2{\text{NO}}_{2}\left(g\right)⇌2\text{NO}\left(g\right)+{\text{O}}_{2}\left(g\right)\)
Calculate the value of the equilibrium constant KP for the reaction \(2\text{NO}\left(g\right)+{\text{Cl}}_{2}\left(g\right)⇌2\text{NOCl}\left(g\right)\) from these equilibrium pressures: NO, 0.050 atm; Cl2, 0.30 atm; NOCl, 1.2 atm.
KP = 1.9 \(×\) 103
When heated, iodine vapor dissociates according to this equation:
\({\text{I}}_{2}\left(g\right)⇌2\text{I}\left(g\right)\)
At 1274 K, a sample exhibits a partial pressure of I2 of 0.1122 atm and a partial pressure due to I atoms of 0.1378 atm. Determine the value of the equilibrium constant, KP, for the decomposition at 1274 K.
A sample of ammonium chloride was heated in a closed container.
\({\text{NH}}_{4}\text{Cl}\left(s\right)⇌{\text{NH}}_{3}\left(g\right)+\text{HCl}\left(g\right)\)
At equilibrium, the pressure of NH3(g) was found to be 1.75 atm. What is the value of the equilibrium constant KP for the decomposition at this temperature?
KP = 3.06
At a temperature of 60 °C, the vapor pressure of water is 0.196 atm. What is the value of the equilibrium constant KP for the vaporization equilibrium at 60 °C?
\({\text{H}}_{2}\text{O}\left(l\right)⇌{\text{H}}_{2}\text{O}\left(g\right)\)
Complete the changes in concentrations (or pressure, if requested) for each of the following reactions.
(a)
\(\begin{array}{llll}2{\text{SO}}_{3}\left(g\right)\hfill & ⇌\hfill & 2{\text{SO}}_{2}\left(g\right)+\hfill & {\text{O}}_{2}\left(g\right)\hfill \\ \text{___}\hfill & & \text{___}\hfill & +x\hfill \\ \text{___}\hfill & & \text{___}\hfill & 0.125\phantom{\rule{0.2em}{0ex}}M\hfill \end{array}\)
(b)
\(\begin{array}{lllll}4{\text{NH}}_{3}\left(g\right)\hfill & +\phantom{\rule{0.2em}{0ex}}3{\text{O}}_{2}\left(g\right)\hfill & ⇌\hfill & 2{\text{N}}_{2}\left(g\right)+\hfill & 6{\text{H}}_{2}\text{O}\left(g\right)\hfill \\ \text{___}\hfill & 3x\hfill & & \text{___}\hfill & \text{___}\hfill \\ \text{___}\hfill & 0.24\phantom{\rule{0.2em}{0ex}}M\hfill & & \text{___}\hfill & \text{___}\hfill \end{array}\)
(c) Change in pressure:
\(\begin{array}{llll}2{\text{CH}}_{4}\left(g\right)\hfill & ⇌\hfill & {\text{C}}_{2}{\text{H}}_{2}\left(g\right)+\hfill & 3{\text{H}}_{2}\left(g\right)\hfill \\ \text{___}\hfill & & x\hfill & \text{___}\hfill \\ \text{___}\hfill & & 25\phantom{\rule{0.2em}{0ex}}\text{torr}\hfill & \text{___}\hfill \end{array}\)
(d) Change in pressure:
\(\begin{array}{lllll}{\text{CH}}_{4}\left(g\right)+\hfill & {\text{H}}_{2}\text{O}\left(g\right)\hfill & ⇌\hfill & \text{CO}\left(g\right)+\hfill & 3{\text{H}}_{2}\left(g\right)\hfill \\ \text{___}\hfill & x\hfill & & \text{___}\hfill & \text{___}\hfill \\ \text{___}\hfill & 5\phantom{\rule{0.2em}{0ex}}\text{atm}\hfill & & \text{___}\hfill & \text{___}\hfill \end{array}\)
(e)
\(\begin{array}{llll}{\text{NH}}_{4}\text{Cl}\left(s\right)\hfill & ⇌\hfill & {\text{NH}}_{3}\left(g\right)+\hfill & \text{HCl}\left(g\right)\hfill \\ & & x\hfill & \text{___}\hfill \\ & & \hfill 1.03\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\phantom{\rule{0.2em}{0ex}}M\hfill & \text{___}\hfill \end{array}\)
(f) change in pressure:
\(\begin{array}{cccc}\text{Ni}\left(s\right)+\hfill & 4\text{CO}\left(g\right)\hfill & ⇌\hfill & \text{Ni}{\left(\text{CO}\right)}_{4}\left(g\right)\hfill \\ & 4x\hfill & & \text{___}\hfill \\ & \hfill 0.40\phantom{\rule{0.2em}{0ex}}\text{atm}\hfill & & \text{___}\hfill \end{array}\)
(a) −2x, 2x, −0.250 M, 0.250 M; (b) 4x, −2x, −6x, 0.32 M, −0.16 M, −0.48 M; (c) −2x, 3x, −50 torr, 75 torr; (d) x, − x, −3x, 5 atm, −5 atm, −15 atm; (e) x, 1.03 \(×\) 10−4M; (f) x, 0.1 atm.
Complete the changes in concentrations (or pressure, if requested) for each of the following reactions.
(a)
\(\begin{array}{cccc}2{\text{H}}_{2}\left(g\right)+\hfill & {\text{O}}_{2}\left(g\right)\hfill & ⇌\hfill & 2{\text{H}}_{2}\text{O}\left(g\right)\hfill \\ \text{___}\hfill & \text{___}\hfill & & +2x\hfill \\ \text{___}\hfill & \text{___}\hfill & & 1.50\phantom{\rule{0.2em}{0ex}}M\hfill \end{array}\)
(b)
\(\begin{array}{ccccc}{\text{CS}}_{2}\left(g\right)+\hfill & 4{\text{H}}_{2}\left(g\right)\hfill & ⇌\hfill & {\text{CH}}_{4}\left(g\right)+\hfill & 2{\text{H}}_{2}\text{S}\left(g\right)\hfill \\ x\hfill & \text{___}\hfill & & \text{___}\hfill & \text{___}\hfill \\ 0.020\phantom{\rule{0.2em}{0ex}}M\hfill & \text{___}\hfill & & \text{___}\hfill & \text{___}\hfill \end{array}\)
(c) Change in pressure:
\(\begin{array}{cccc}{\text{H}}_{2}\left(g\right)+\hfill & {\text{Cl}}_{2}\left(g\right)\hfill & ⇌\hfill & 2\text{HCl}\left(g\right)\hfill \\ x\hfill & \text{___}\hfill & & \text{___}\hfill \\ 1.50\phantom{\rule{0.2em}{0ex}}\text{atm}\hfill & \text{___}\hfill & & \text{___}\hfill \end{array}\)
(d) Change in pressure:
\(\begin{array}{ccccc}2{\text{NH}}_{3}\left(g\right)\hfill & +\phantom{\rule{0.2em}{0ex}}2{\text{O}}_{2}\left(g\right)\hfill & ⇌\hfill & {\text{N}}_{2}\text{O}\left(g\right)+\hfill & 3{\text{H}}_{2}\text{O}\left(g\right)\hfill \\ \text{___}\hfill & \text{___}\hfill & & \text{___}\hfill & x\hfill \\ \text{___}\hfill & \text{___}\hfill & & \text{___}\hfill & 60.6\phantom{\rule{0.2em}{0ex}}\text{torr}\hfill \end{array}\)
(e)
\(\begin{array}{cccc}{\text{NH}}_{4}\text{HS}\left(s\right)\hfill & ⇌\hfill & {\text{NH}}_{3}\left(g\right)+\hfill & {\text{H}}_{2}\text{S}\left(g\right)\hfill \\ & & x\hfill & \text{___}\hfill \\ & & 9.8\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}M\hfill & \text{___}\hfill \end{array}\)
(f) Change in pressure:
\(\begin{array}{cccc}\text{Fe}\left(s\right)+\hfill & 5\text{CO}\left(g\right)\hfill & ⇌\hfill & \text{Fe}{\left(\text{CO}\right)}_{5}\left(g\right)\hfill \\ & \text{___}\hfill & & x\hfill \\ & \text{___}\hfill & & 0.012\phantom{\rule{0.2em}{0ex}}\text{atm}\hfill \end{array}\)
Why are there no changes specified for Ni in (Figure), part (f)? What property of Ni does change?
Activities of pure crystalline solids equal 1 and are constant; however, the mass of Ni does change.
Why are there no changes specified for NH4HS in (Figure), part (e)? What property of NH4HS does change?
Analysis of the gases in a sealed reaction vessel containing NH3, N2, and H2 at equilibrium at 400 °C established the concentration of N2 to be 1.2 M and the concentration of H2 to be 0.24 M.
\({\text{N}}_{2}\left(g\right)+3{\text{H}}_{2}\left(g\right)⇌2{\text{NH}}_{3}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{c}=0.50\phantom{\rule{0.2em}{0ex}}\text{at}\phantom{\rule{0.2em}{0ex}}400\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}\)
Calculate the equilibrium molar concentration of NH3.
[NH3] = 9.1 \(×\) 10−2M
Calculate the number of moles of HI that are at equilibrium with 1.25 mol of H2 and 1.25 mol of I2 in a 5.00−L flask at 448 °C.
\({\text{H}}_{2}+{\text{I}}_{2}⇌2\text{HI}\phantom{\rule{5em}{0ex}}{K}_{c}=50.2\phantom{\rule{0.2em}{0ex}}\text{at}\phantom{\rule{0.2em}{0ex}}448\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}\)
What is the pressure of BrCl in an equilibrium mixture of Cl2, Br2, and BrCl if the pressure of Cl2 in the mixture is 0.115 atm and the pressure of Br2 in the mixture is 0.450 atm?
\({\text{Cl}}_{2}\left(g\right)+{\text{Br}}_{2}\left(g\right)⇌2\text{BrCl}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{P}=4.7\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}\)
PBrCl = 4.9 \(×\) 10−2 atm
What is the pressure of CO2 in a mixture at equilibrium that contains 0.50 atm H2, 2.0 atm of H2O, and 1.0 atm of CO at 990 °C?
\({\text{H}}_{2}\left(g\right)+{\text{CO}}_{2}\left(g\right)⇌{\text{H}}_{2}\text{O}\left(g\right)+\text{CO}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{P}=1.6\phantom{\rule{0.2em}{0ex}}\text{at}\phantom{\rule{0.2em}{0ex}}990\phantom{\rule{0.2em}{0ex}}\text{°C}\)
Cobalt metal can be prepared by reducing cobalt(II) oxide with carbon monoxide.
\(\text{CoO}\left(s\right)+\text{CO}\left(g\right)⇌\text{Co}\left(s\right)+{\text{CO}}_{2}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{c}=4.90\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{2}\text{at}\phantom{\rule{0.2em}{0ex}}550\phantom{\rule{0.2em}{0ex}}\text{°C}\)
What concentration of CO remains in an equilibrium mixture with [CO2] = 0.100 M?
[CO] = 2.04 \(×\) 10−4M
Carbon reacts with water vapor at elevated temperatures.
\(\text{C}\left(s\right)+{\text{H}}_{2}\text{O}\left(g\right)⇌\text{CO}\left(g\right)+{\text{H}}_{2}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{c}=0.2\phantom{\rule{0.2em}{0ex}}\text{at}\phantom{\rule{0.2em}{0ex}}1000\phantom{\rule{0.2em}{0ex}}\text{°C}\)
Assuming a reaction mixture initially contains only reactants, what is the concentration of CO in an equilibrium mixture with [H2O] = 0.500 M at 1000 °C?
Sodium sulfate 10−hydrate, Na2SO4·10H2O, dehydrates according to the equation
\({\text{Na}}_{2}{\text{SO}}_{4}\text{·}10{\text{H}}_{2}\text{O}\left(s\right)⇌{\text{Na}}_{2}{\text{SO}}_{4}\left(s\right)+10{\text{H}}_{2}\text{O}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{P}=4.08\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-25}\phantom{\rule{0.2em}{0ex}}\text{at}\phantom{\rule{0.2em}{0ex}}25\phantom{\rule{0.2em}{0ex}}\text{°C}\)
What is the pressure of water vapor at equilibrium with a mixture of Na2SO4·10H2O and NaSO4?
\({P}_{{\text{H}}_{\text{2}}}{}_{\text{O}}=3.64\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−3}}\phantom{\rule{0.2em}{0ex}}\text{atm}\)
Calcium chloride 6−hydrate, CaCl2·6H2O, dehydrates according to the equation
\({\text{CaCl}}_{\text{2}}\text{·}6{\text{H}}_{2}\text{O}\left(s\right)⇌{\text{CaCl}}_{2}\left(s\right)+6{\text{H}}_{2}\text{O}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{P}=5.09\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-44}\phantom{\rule{0.2em}{0ex}}\text{at}\phantom{\rule{0.2em}{0ex}}25\phantom{\rule{0.2em}{0ex}}\text{°C}\)
What is the pressure of water vapor at equilibrium with a mixture of CaCl2·6H2O and CaCl2 at 25 °C?
A student solved the following problem and found the equilibrium concentrations to be [SO2] = 0.590 M, [O2] = 0.0450 M, and [SO3] = 0.260 M. How could this student check the work without reworking the problem? The problem was: For the following reaction at 600 °C:
\(2{\text{SO}}_{2}\left(g\right)+{\text{O}}_{2}\left(g\right)⇌2{\text{SO}}_{3}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{c}=4.32\)
What are the equilibrium concentrations of all species in a mixture that was prepared with [SO3] = 0.500 M, [SO2] = 0 M, and [O2] = 0.350 M?
Calculate Q based on the calculated concentrations and see if it is equal to Kc. Because Q does equal 4.32, the system must be at equilibrium.
A student solved the following problem and found [N2O4] = 0.16 M at equilibrium. How could this student recognize that the answer was wrong without reworking the problem? The problem was: What is the equilibrium concentration of N2O4 in a mixture formed from a sample of NO2 with a concentration of 0.10 M?
\(2{\text{NO}}_{2}\left(g\right)⇌{\text{N}}_{2}{\text{O}}_{4}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{c}=160\)
Assume that the change in concentration of N2O4 is small enough to be neglected in the following problem.
(a) Calculate the equilibrium concentration of both species in 1.00 L of a solution prepared from 0.129 mol of N2O4 with chloroform as the solvent.
\({\text{N}}_{2}{\text{O}}_{4}\left(g\right)⇌2{\text{NO}}_{2}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{c}=1.07\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\) in chloroform
(b) Confirm that the change is small enough to be neglected.
(a) [NO2] = 1.17 \(×\) 10−3M
[N2O4] = 0.128 M
(b) The assumption that x is negligibly small compared to 0.129 is confirmed by comparing the initial concentration of the N2O4 to its concentration at equilibrium (they differ by just 1 in the least significant digit’s place).
Assume that the change in concentration of COCl2 is small enough to be neglected in the following problem.
(a) Calculate the equilibrium concentration of all species in an equilibrium mixture that results from the decomposition of COCl2 with an initial concentration of 0.3166 M.
\({\text{COCl}}_{2}\left(g\right)⇌\text{CO}\left(g\right)+{\text{Cl}}_{2}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{c}=2.2\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-10}\)
(b) Confirm that the change is small enough to be neglected.
Assume that the change in pressure of H2S is small enough to be neglected in the following problem.
(a) Calculate the equilibrium pressures of all species in an equilibrium mixture that results from the decomposition of H2S with an initial pressure of 0.824 atm.
\(2{\text{H}}_{2}\text{S}\left(g\right)⇌2{\text{H}}_{2}\left(g\right)+{\text{S}}_{2}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{P}=2.2\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\)
(b) Confirm that the change is small enough to be neglected.
(a) [H2S] = 0.810 atm
[H2] = 0.014 atm
[S2] = 0.0072 atm
(b) The assumption that 2x is negligibly small compared to 0.824 is confirmed by comparing the initial concentration of the H2S to its concentration at equilibrium (0.824 atm versus 0.810 atm, a difference of less than 2%).
What are all concentrations after a mixture that contains [H2O] = 1.00 M and [Cl2O] = 1.00 M comes to equilibrium at 25 °C?
\({\text{H}}_{2}\text{O}\left(g\right)+{\text{Cl}}_{2}\text{O}\left(g\right)⇌2\text{HOCl}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{c}=0.0900\)
Calculate the number of grams of HI that are at equilibrium with 1.25 mol of H2 and 63.5 g of iodine at 448 °C.
\({\text{H}}_{2}+{\text{I}}_{2}⇌2\text{HI}\phantom{\rule{5em}{0ex}}{K}_{c}=50.2\phantom{\rule{0.2em}{0ex}}\text{at}\phantom{\rule{0.2em}{0ex}}448\phantom{\rule{0.2em}{0ex}}\text{°C}\)
507 g
Butane exists as two isomers, n−butane and isobutane.
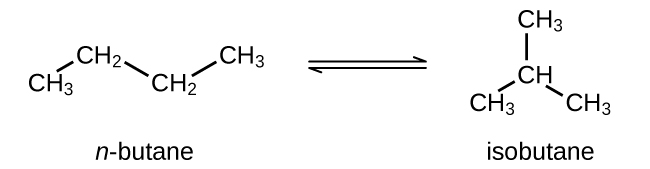
KP = 2.5 at 25 °C
What is the pressure of isobutane in a container of the two isomers at equilibrium with a total pressure of 1.22 atm?
What is the minimum mass of CaCO3 required to establish equilibrium at a certain temperature in a 6.50-L container if the equilibrium constant (Kc) is 0.50 for the decomposition reaction of CaCO3 at that temperature?
\({\text{CaCO}}_{3}\left(s\right)⇌\text{CaO}\left(s\right)+{\text{CO}}_{2}\left(g\right)\)
330 g
The equilibrium constant (Kc) for this reaction is 1.60 at 990 °C:
\({\text{H}}_{2}\left(g\right)+{\text{CO}}_{2}\left(g\right)⇌{\text{H}}_{2}\text{O}\left(g\right)+\text{CO}\left(g\right)\)
Calculate the number of moles of each component in the final equilibrium mixture obtained from adding 1.00 mol of H2, 2.00 mol of CO2, 0.750 mol of H2O, and 1.00 mol of CO to a 5.00-L container at 990 °C.
In a 3.0-L vessel, the following equilibrium partial pressures are measured: N2, 190 torr; H2, 317 torr; NH3, 1.00 \(×\) 103 torr.
\({\text{N}}_{2}\left(g\right)+3{\text{H}}_{2}\left(g\right)⇌2{\text{NH}}_{3}\left(g\right)\)
(a) How will the partial pressures of H2, N2, and NH3 change if H2 is removed from the system? Will they increase, decrease, or remain the same?
(b) Hydrogen is removed from the vessel until the partial pressure of nitrogen, at equilibrium, is 250 torr. Calculate the partial pressures of the other substances under the new conditions.
The equilibrium constant (Kc) for this reaction is 5.0 at a given temperature.
\(\text{CO}\left(g\right)+{\text{H}}_{2}\text{O}\left(g\right)⇌{\text{CO}}_{2}\left(g\right)+{\text{H}}_{2}\left(g\right)\)
(a) On analysis, an equilibrium mixture of the substances present at the given temperature was found to contain 0.20 mol of CO, 0.30 mol of water vapor, and 0.90 mol of H2 in a liter. How many moles of CO2 were there in the equilibrium mixture?
(b) Maintaining the same temperature, additional H2 was added to the system, and some water vapor was removed by drying. A new equilibrium mixture was thereby established containing 0.40 mol of CO, 0.30 mol of water vapor, and 1.2 mol of H2 in a liter. How many moles of CO2 were in the new equilibrium mixture? Compare this with the quantity in part (a), and discuss whether the second value is reasonable. Explain how it is possible for the water vapor concentration to be the same in the two equilibrium solutions even though some vapor was removed before the second equilibrium was established.
(a) 0.33 mol.
(b) [CO]2 = 0.50 M. Added H2 forms some water as a result of a shift to the left after H2 is added.
Antimony pentachloride decomposes according to this equation:
\({\text{SbCl}}_{5}\left(g\right)⇌{\text{SbCl}}_{3}\left(g\right)+{\text{Cl}}_{2}\left(g\right)\)
An equilibrium mixture in a 5.00-L flask at 448 °C contains 3.85 g of SbCl5, 9.14 g of SbCl3, and 2.84 g of Cl2. How many grams of each will be found if the mixture is transferred into a 2.00-L flask at the same temperature?
Consider the equilibrium
\(4{\text{NO}}_{2}\left(g\right)+6{\text{H}}_{2}\text{O}\left(g\right)⇌4{\text{NH}}_{3}\left(g\right)+7{\text{O}}_{2}\left(g\right)\)
(a) What is the expression for the equilibrium constant (Kc) of the reaction?
(b) How must the concentration of NH3 change to reach equilibrium if the reaction quotient is less than the equilibrium constant?
(c) If the reaction were at equilibrium, how would an increase in the volume of the reaction vessel affect the pressure of NO2?
(d) If the change in the pressure of NO2 is 28 torr as a mixture of the four gases reaches equilibrium, how much will the pressure of O2 change?
(a) \({K}_{c}=\phantom{\rule{0.2em}{0ex}}\frac{{\left[{\text{NH}}_{3}\right]}^{4}{\left[{\text{O}}_{2}\right]}^{7}}{{\left[{\text{NO}}_{2}\right]}^{4}{\left[{\text{H}}_{2}\text{O}\right]}^{6}}.\) (b) [NH3] must increase for Qc to reach Kc. (c) The increase in system volume would lower the partial pressures of all reactants (including NO2). (d) \({P}_{{\text{O}}_{\text{2}}}=49\phantom{\rule{0.2em}{0ex}}\text{torr}\)
The binding of oxygen by hemoglobin (Hb), giving oxyhemoglobin (HbO2), is partially regulated by the concentration of H3O+ and dissolved CO2 in the blood. Although the equilibrium is complicated, it can be summarized as
\({\text{HbO}}_{2}\left(aq\right)+{\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{CO}}_{2}\left(g\right)⇌{\text{CO}}_{2}\text{−}\text{Hb}\text{−}{\text{H}}^{\text{+}}+{\text{O}}_{2}\left(g\right)+{\text{H}}_{2}\text{O}\left(l\right)\)
(a) Write the equilibrium constant expression for this reaction.
(b) Explain why the production of lactic acid and CO2 in a muscle during exertion stimulates release of O2 from the oxyhemoglobin in the blood passing through the muscle.
Liquid N2O3 is dark blue at low temperatures, but the color fades and becomes greenish at higher temperatures as the compound decomposes to NO and NO2. At 25 °C, a value of KP = 1.91 has been established for this decomposition. If 0.236 moles of N2O3 are placed in a 1.52-L vessel at 25 °C, calculate the equilibrium partial pressures of N2O3(g), NO2(g), and NO(g).
\({P}_{{\text{N}}_{\text{2}}}{}_{{\text{O}}_{\text{3}}}=1.90\phantom{\rule{0.2em}{0ex}}\text{atm and}\phantom{\rule{0.2em}{0ex}}{P}_{\text{NO}}={P}_{{\text{NO}}_{\text{2}}}=1.90\phantom{\rule{0.2em}{0ex}}\text{atm}\)
A 1.00-L vessel at 400 °C contains the following equilibrium concentrations: N2, 1.00 M; H2, 0.50 M; and NH3, 0.25 M. How many moles of hydrogen must be removed from the vessel to increase the concentration of nitrogen to 1.1 M? The equilibrium reaction is
\({\text{N}}_{2}\left(g\right)+3{\text{H}}_{2}\left(g\right)⇌2{\text{NH}}_{3}\left(g\right)\)
Calculate the equilibrium constant at 25 °C for each of the following reactions from the value of ΔG° given.
(a) \({\text{I}}_{2}\left(s\right)+{\text{Cl}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{2ICl}\left(g\right)\phantom{\rule{5em}{0ex}}\text{Δ}G\text{°}=\text{−10.88 kJ}\)
(b) \({\text{H}}_{2}\left(g\right)+{\text{I}}_{2}\left(s\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{2HI}\left(g\right)\phantom{\rule{5em}{0ex}}\text{Δ}G\text{°}=\text{3.4 kJ}\)
(c) \({\text{CS}}_{2}\left(g\right)+{\text{3Cl}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{CCl}}_{4}\left(g\right)+{\text{S}}_{2}{\text{Cl}}_{2}\left(g\right)\phantom{\rule{5em}{0ex}}\text{Δ}G\text{°}=\text{−39 kJ}\)
(d) \({\text{2SO}}_{2}\left(g\right)+{\text{O}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{2SO}}_{3}\left(g\right)\phantom{\rule{5em}{0ex}}\text{Δ}G\text{°}=\text{−141.82 kJ}\)
(e) \({\text{CS}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{CS}}_{2}\left(l\right)\phantom{\rule{5em}{0ex}}\text{Δ}G\text{°}=\text{−1.88 kJ}\)
Calculate the equilibrium constant at the temperature given.
(a) \({\text{O}}_{2}\left(g\right)+{\text{2F}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{2F}}_{2}\text{O}\left(g\right)\phantom{\rule{5em}{0ex}}\left(\text{T}=100\phantom{\rule{0.2em}{0ex}}\text{°C}\right)\)
(b) \({\text{I}}_{2}\left(s\right)+{\text{Br}}_{2}\left(l\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{2IBr}\left(g\right)\phantom{\rule{5em}{0ex}}\left(\text{T}=0.0\phantom{\rule{0.2em}{0ex}}\text{°C}\right)\)
(c) \(\text{2LiOH}\left(s\right)+{\text{CO}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{Li}}_{2}{\text{CO}}_{3}\left(s\right)+{\text{H}}_{2}\text{O}\left(g\right)\phantom{\rule{5em}{0ex}}\left(\text{T}=575\phantom{\rule{0.2em}{0ex}}\text{°C}\right)\)
(d) \({\text{N}}_{2}{\text{O}}_{3}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{NO}\left(g\right)+{\text{NO}}_{2}\left(g\right)\phantom{\rule{5em}{0ex}}\left(\text{T}=-10.0\phantom{\rule{0.2em}{0ex}}\text{°C}\right)\)
(e) \({\text{SnCl}}_{4}\left(l\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{SnCl}}_{4}\left(g\right)\phantom{\rule{5em}{0ex}}\left(\text{T}=200\phantom{\rule{0.2em}{0ex}}\text{°C}\right)\)
In each of the following, the value of ΔG is not given at the temperature of the reaction. Therefore, we must calculate ΔG from the values ΔH° and ΔS and then calculate ΔG from the relation ΔG = ΔH° − TΔS°.
(a) K = 1.29;
(b) K = 2.51 \(×\) 10−3;
(c) K = 4.83 \(×\) 103;
(d) K = 0.219;
(e) K = 16.1
Calculate the equilibrium constant at the temperature given.
(a) \({\text{I}}_{2}\left(s\right)+{\text{Cl}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{2ICl}\left(g\right)\phantom{\rule{5em}{0ex}}\left(\text{T}=100\phantom{\rule{0.2em}{0ex}}\text{°C}\right)\)
(b) \({\text{H}}_{2}\left(g\right)+{\text{I}}_{2}\left(s\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{2HI}\left(g\right)\phantom{\rule{5em}{0ex}}\left(\text{T}=0.0\phantom{\rule{0.2em}{0ex}}\text{°C}\right)\)
(c) \({\text{CS}}_{2}\left(g\right)+{\text{3Cl}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{CCl}}_{4}\left(g\right)+{\text{S}}_{2}{\text{Cl}}_{2}\left(g\right)\phantom{\rule{5em}{0ex}}\left(\text{T}=125\phantom{\rule{0.2em}{0ex}}\text{°C}\right)\)
(d) \({\text{2SO}}_{2}\left(g\right)+{\text{O}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{2SO}}_{3}\left(g\right)\phantom{\rule{5em}{0ex}}\left(\text{T}=675\phantom{\rule{0.2em}{0ex}}\text{°C}\right)\)
(e) \({\text{CS}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{CS}}_{2}\left(l\right)\phantom{\rule{5em}{0ex}}\left(\text{T}=90\phantom{\rule{0.2em}{0ex}}\text{°C}\right)\)
Consider the following reaction at 298 K:
\({\text{N}}_{2}{\text{O}}_{4}\left(g\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}{\text{2NO}}_{2}\left(g\right)\phantom{\rule{5em}{0ex}}{K}_{P}=0.142\)
What is the standard free energy change at this temperature? Describe what happens to the initial system, where the reactants and products are in standard states, as it approaches equilibrium.
The standard free energy change is \(\text{Δ}{G}_{298}^{°}=\text{−}RT\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}K=\text{4.84 kJ/mol}.\) When reactants and products are in their standard states (1 bar or 1 atm), Q = 1. As the reaction proceeds toward equilibrium, the reaction shifts left (the amount of products drops while the amount of reactants increases): Q < 1, and \(\text{Δ}{G}_{298}\) becomes less positive as it approaches zero. At equilibrium, Q = K, and ΔG = 0.
Determine the normal boiling point (in kelvin) of dichloroethane, CH2Cl2. Find the actual boiling point using the Internet or some other source, and calculate the percent error in the temperature. Explain the differences, if any, between the two values.
Under what conditions is \({\text{N}}_{2}{\text{O}}_{3}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{NO}\left(g\right)+{\text{NO}}_{2}\left(g\right)\) spontaneous?
The reaction will be spontaneous at temperatures greater than 287 K.
At room temperature, the equilibrium constant (Kw) for the self-ionization of water is 1.00 \(×\) 10−14. Using this information, calculate the standard free energy change for the aqueous reaction of hydrogen ion with hydroxide ion to produce water. (Hint: The reaction is the reverse of the self-ionization reaction.)
Hydrogen sulfide is a pollutant found in natural gas. Following its removal, it is converted to sulfur by the reaction \({\text{2H}}_{2}\text{S}\left(g\right)+{\text{SO}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}\frac{3}{8}{\text{S}}_{8}\left(s,\phantom{\rule{0.2em}{0ex}}\text{rhombic}\right)+{\text{2H}}_{2}\text{O}\left(l\right).\) What is the equilibrium constant for this reaction? Is the reaction endothermic or exothermic?
K = 5.35 \(×\) 1015
The process is exothermic.
Consider the decomposition of CaCO3(s) into CaO(s) and CO2(g). What is the equilibrium partial pressure of CO2 at room temperature?
In the laboratory, hydrogen chloride (HCl(g)) and ammonia (NH3(g)) often escape from bottles of their solutions and react to form the ammonium chloride (NH4Cl(s)), the white glaze often seen on glassware. Assuming that the number of moles of each gas that escapes into the room is the same, what is the maximum partial pressure of HCl and NH3 in the laboratory at room temperature? (Hint: The partial pressures will be equal and are at their maximum value when at equilibrium.)
1.0 \(×\) 10−8 atm. This is the maximum pressure of the gases under the stated conditions.
Benzene can be prepared from acetylene. \({\text{3C}}_{2}{\text{H}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⇌\phantom{\rule{0.2em}{0ex}}{\text{C}}_{6}{\text{H}}_{6}\left(g\right).\) Determine the equilibrium constant at 25 °C and at 850 °C. Is the reaction spontaneous at either of these temperatures? Why is all acetylene not found as benzene?
Carbon dioxide decomposes into CO and O2 at elevated temperatures. What is the equilibrium partial pressure of oxygen in a sample at 1000 °C for which the initial pressure of CO2 was 1.15 atm?
\(x=1.29\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\phantom{\rule{0.2em}{0ex}}\text{atm}={P}_{{\text{O}}_{2}}\)
Carbon tetrachloride, an important industrial solvent, is prepared by the chlorination of methane at 850 K.
\({\text{CH}}_{4}\left(g\right)+{\text{4Cl}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{CCl}}_{4}\left(g\right)+\text{4HCl}\left(g\right)\)
What is the equilibrium constant for the reaction at 850 K? Would the reaction vessel need to be heated or cooled to keep the temperature of the reaction constant?
Acetic acid, CH3CO2H, can form a dimer, (CH3CO2H)2, in the gas phase.
\({\text{2CH}}_{3}{\text{CO}}_{2}\text{H}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\left({\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right)}_{2}\left(g\right)\)
The dimer is held together by two hydrogen bonds with a total strength of 66.5 kJ per mole of dimer.
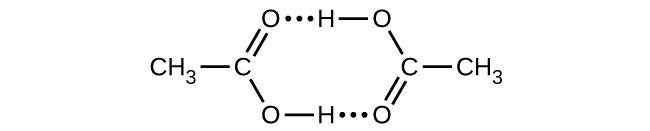
At 25 °C, the equilibrium constant for the dimerization is 1.3 \(×\) 103 (pressure in atm). What is ΔS° for the reaction?
−0.16 kJ

