181 Lewis Acids and Bases

Paul Flowers; Edward J. Neth; William R. Robinson; Klaus Theopold; and Richard Langley

[latexpage]

Learning Objectives

By the end of this section, you will be able to:

  • Explain the Lewis model of acid-base chemistry
  • Write equations for the formation of adducts and complex ions
  • Perform equilibrium calculations involving formation constants

In 1923, G. N. Lewis proposed a generalized definition of acid-base behavior in which acids and bases are identified by their ability to accept or to donate a pair of electrons and form a coordinate covalent bond.

A coordinate covalent bond (or dative bond) occurs when one of the atoms in the bond provides both bonding electrons. For example, a coordinate covalent bond occurs when a water molecule combines with a hydrogen ion to form a hydronium ion. A coordinate covalent bond also results when an ammonia molecule combines with a hydrogen ion to form an ammonium ion. Both of these equations are shown here.

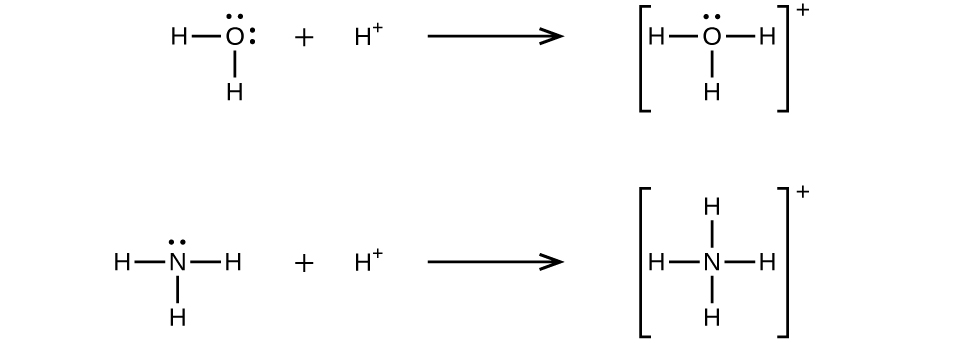
This figure shows two reactions represented with Lewis structures. The first shows an O atom bonded to two H atoms. The O atom has two lone pairs of electrons. There is a plus sign and then an H atom with a superscript positive sign followed by a right-facing arrow. The next Lewis structure is in brackets and shows an O atom bonded to three H atoms. There is one lone pair of electrons on the O atom. Outside of the brackets is a superscript positive sign. The second reaction shows an N atom bonded to three H atoms. The N atom has one lone pair of electrons. There is a plus sign and then an H superscript positive sign. After the H superscript positive sign is a right-facing arrow. The next Lewis structure is in brackets. It shows an N atom bonded to four H atoms. There is a superscript positive sign outside the brackets.

Reactions involving the formation of coordinate covalent bonds are classified as Lewis acid-base chemistry. The species donating the electron pair that compose the bond is a Lewis base, the species accepting the electron pair is a Lewis acid, and the product of the reaction is a Lewis acid-base adduct. As the two examples above illustrate, Brønsted-Lowry acid-base reactions represent a subcategory of Lewis acid reactions, specifically, those in which the acid species is H+. A few examples involving other Lewis acids and bases are described below.

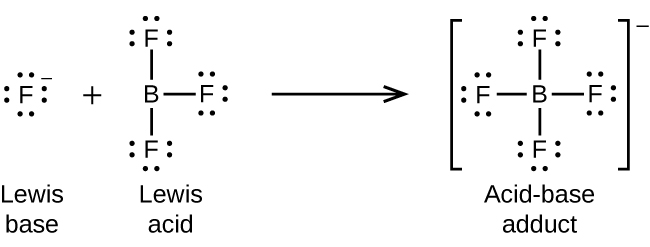
The boron atom in boron trifluoride, BF3, has only six electrons in its valence shell. Being short of the preferred octet, BF3 is a very good Lewis acid and reacts with many Lewis bases; a fluoride ion is the Lewis base in this reaction, donating one of its lone pairs:

This figure illustrates a chemical reaction using structural formulas. On the left, an F atom is surrounded by four electron dot pairs and has a superscript negative symbol. This structure is labeled below as “Lewis base.” Following a plus sign is another structure which has a B atom at the center and three F atoms single bonded above, right, and below. Each F atom has three pairs of electron dots. This structure is labeled below as “Lewis acid.” Following a right pointing arrow is a structure in brackets that has a central B atom to which 4 F atoms are connected with single bonds above, below, to the left, and to the right. Each F atom in this structure has three pairs of electron dots. Outside the brackets is a superscript negative symbol. This structure is labeled below as “Acid-base adduct.”

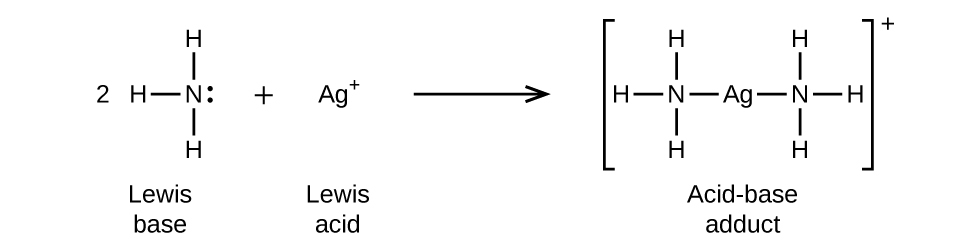
In the following reaction, each of two ammonia molecules, Lewis bases, donates a pair of electrons to a silver ion, the Lewis acid:

This figure illustrates a chemical reaction using structural formulas. On the left side, a 2 preceeds an N atom which has H atoms single bonded above, to the left, and below. A single electron dot pair is on the right side of the N atom. This structure is labeled below as “Lewis base.” Following a plus sign is an A g atom which has a superscript plus symbol. Following a right pointing arrow is a structure in brackets that has a central A g atom to which N atoms are connected with single bonds to the left and to the right. Each of these N atoms has H atoms bonded above, below, and to the outside of the structure. Outside the brackets is a superscript plus symbol. This structure is labeled below as “Acid-base adduct.”

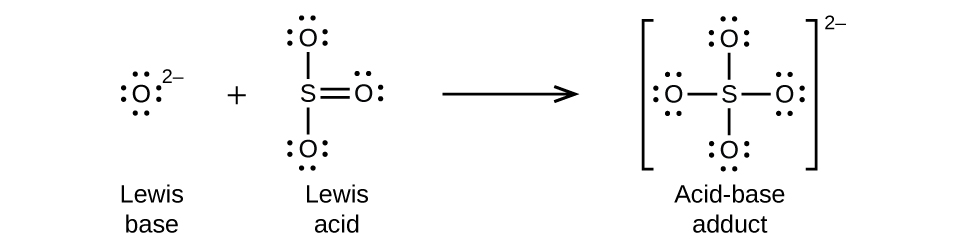
Nonmetal oxides act as Lewis acids and react with oxide ions, Lewis bases, to form oxyanions:

This figure illustrates a chemical reaction using structural formulas. On the left, an O atom is surrounded by four electron dot pairs and has a superscript 2 negative. This structure is labeled below as “Lewis base.” Following a plus sign is another structure which has an S atom at the center. O atoms are single bonded above and below. These O atoms have three electron dot pairs each. To the right of the S atom is a double bonded O atom which has two pairs of electron dots. This structure is labeled below as “Lewis acid.” Following a right pointing arrow is a structure in brackets that has a central S atom to which 4 O atoms are connected with single bonds above, below, to the left, and to the right. Each of the O atoms has three pairs of electron dots. Outside the brackets is a superscript 2 negative. This structure is labeled below as “Acid-base adduct.”

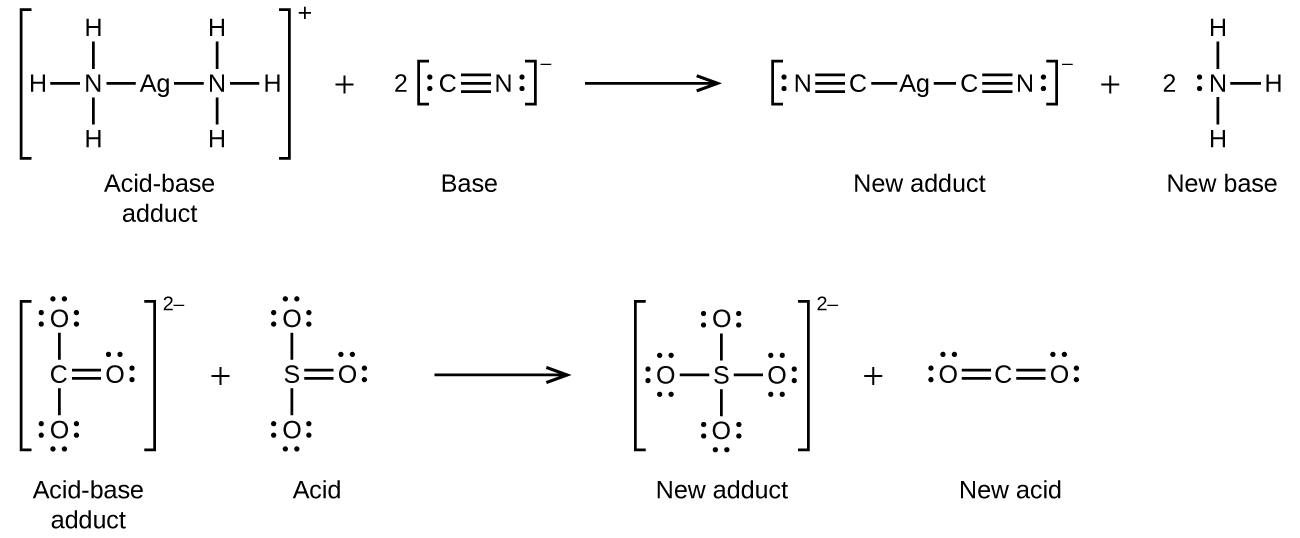
Many Lewis acid-base reactions are displacement reactions in which one Lewis base displaces another Lewis base from an acid-base adduct, or in which one Lewis acid displaces another Lewis acid:

Two chemical reactions in two rows using structural formulas. First row, to the left, in brackets is a structure with a central A g atom to which N atoms are connected with single bonds to the left and right. Each N atom has H atoms bonded above, below, and to the outside. Outside the brackets is a superscript plus symbol. This structure is labeled “Acid-base adduct.” Following a plus sign is a 2 and another structure in brackets that shows a C atom triple bonded to an N atom. The C atom has an unshared electron pair on its left side and the N atom has an unshared pair on its right side. Outside the brackets to the right is a superscript negative symbol. This structure is labeled “Base.” Following a right pointing arrow is a structure in brackets with a central A g atom to which 4 FC atoms are connected with single bonds to the left and right. At each of the two ends, N atoms are triple bonded to the C atoms. The N atoms each have an unshared electron pair at the end of the structure. Outside the brackets is a superscript negative symbol. This structure is labeled “New adduct.” Following a plus sign is an N atom with H atoms single bonded above, to the left, and below. A single electron dot pair is on the left side of the N atom. This structure is labeled “New base.” In the second row, on the left side in brackets is a structure with a central C atom. O atoms, each with three unshared electron pairs, are single bonded above and below and a third O atom, with two unshared electron pairs, is double bonded to the right. Outside the brackets is a superscript 2 negative. This structure is labeled “Acid-base adduct.” Following a plus sign is another structure with an S atom at the center. O atoms are single bonded above and below. These O atoms have three electron dot pairs each. To the right of the S atom is a double bonded O atom which has two pairs of electron dots. This structure is labeled “Acid.” Following a right pointing arrow is a structure in brackets with a central S atom to which 4 O atoms are connected with single bonds above, below, left, and right. Each of the O atoms has three pairs of electron dots. Outside the brackets is a superscript 2 negative. This structure is labeled “New adduct.” Following a plus sign is a structure with a central C atom that has two O atoms, each with two unshared electron pairs, double bonded to the left and right.

Another type of Lewis acid-base chemistry involves the formation of a complex ion (or a coordination complex) comprising a central atom, typically a transition metal cation, surrounded by ions or molecules called ligands. These ligands can be neutral molecules like H2O or NH3, or ions such as CN– or OH–. Often, the ligands act as Lewis bases, donating a pair of electrons to the central atom. These types of Lewis acid-base reactions are examples of a broad subdiscipline called coordination chemistry—the topic of another chapter in this text.

The equilibrium constant for the reaction of a metal ion with one or more ligands to form a coordination complex is called a formation constant (Kf) (sometimes called a stability constant). For example, the complex ion \(\text{Cu}{\left(\text{CN}\right)}_{2}{}^{\text{−}}\)

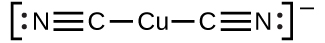
A Cu atom is bonded to two C atoms. Each of these C atoms is triple bonded to an N atom. Each N atom has two dots on the side of it.

is produced by the reaction

\({\text{Cu}}^{\text{+}}\left(aq\right)+2{\text{CN}}^{\text{−}}\left(aq\right)⇌\text{Cu}{\left(\text{CN}\right)}_{2}{}^{\text{−}}\left(aq\right)\)

The formation constant for this reaction is

\({K}_{\text{f}}=\frac{\left[\text{Cu}{\left(\text{CN}\right)}_{2}{}^{\text{−}}\right]}{\left[{\text{Cu}}^{+}\right]{\left[{\text{CN}}^{\text{−}}\right]}^{2}}\)

Alternatively, the reverse reaction (decomposition of the complex ion) can be considered, in which case the equilibrium constant is a dissociation constant (Kd). Per the relation between equilibrium constants for reciprocal reactions described, the dissociation constant is the mathematical inverse of the formation constant, Kd = Kf–1. A tabulation of formation constants is provided in Appendix K.

As an example of dissolution by complex ion formation, let us consider what happens when we add aqueous ammonia to a mixture of silver chloride and water. Silver chloride dissolves slightly in water, giving a small concentration of Ag+ ([Ag+] = 1.3 \(×\) 10–5M):

\(\text{AgCl}\left(s\right)⇌{\text{Ag}}^{\text{+}}\left(aq\right)+{\text{Cl}}^{\text{−}}\left(aq\right)\)

However, if NH3 is present in the water, the complex ion, \(\text{Ag}{\left({\text{NH}}_{3}\right)}_{2}{}^{+},\) can form according to the equation:

Dissociation of a Complex Ion Calculate the concentration of the silver ion in a solution that initially is 0.10 M with respect to \(\text{Ag}{\left({\text{NH}}_{3}\right)}_{2}{}^{+}.\)

Solution Applying the standard ICE approach to this reaction yields the following:

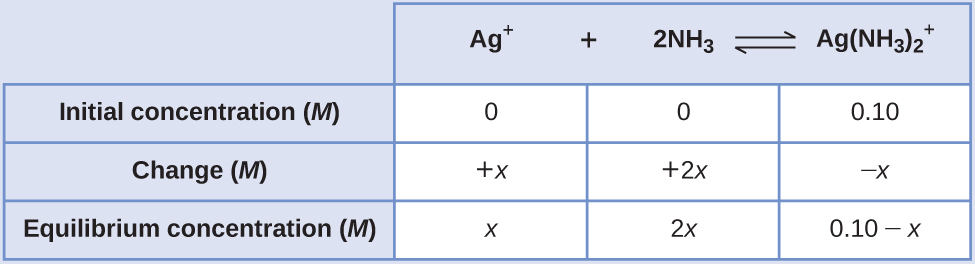
This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ), Change ( M ), and Equilibrium concentration ( M ). The second column has the header, “A g superscript positive sign plus 2 N H subscript 3 equilibrium sign A g ( N H subscript 3 ) subscript 2 superscript positive sign.” Under the second column is a subgroup of three rows and three columns. The first column contains: 0, positive x, x. The second column contains: 0, positive 2 x, 2 x. The third column contains 0.10, negative x, and 0.10 minus x.

Substituting these equilibrium concentration terms into the Kf expression gives

\({K}_{\text{f}}=\frac{\left[\text{Ag}{\left({\text{NH}}_{3}\right)}_{2}{}^{+}\right]}{\left[{\text{Ag}}^{+}\right]{\left[{\text{NH}}_{3}\right]}^{2}}\)
\(1.7\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{7}\phantom{\rule{0.2em}{0ex}}\text{=}\phantom{\rule{0.2em}{0ex}}\frac{0.10-x}{\left(x\right){\left(2x\right)}^{2}}\)

The very large equilibrium constant means the amount of the complex ion that will dissociate, x, will be very small. Assuming x << 0.1 permits simplifying the above equation:

\(1.7\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{7}=\frac{0.10}{\left(x\right){\left(2x\right)}^{2}}\)
\({x}^{3}=\frac{0.10}{4\left(1.7\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{7}\right)}\phantom{\rule{0.2em}{0ex}}=1.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}\)
\(x\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}\sqrt[3]{1.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}}\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}1.1\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\)

Because only 1.1% of the \(\text{Ag}{\left({\text{NH}}_{3}\right)}_{2}{}^{+}\) dissociates into Ag+ and NH3, the assumption that x is small is justified.

Using this value of x and the relations in the above ICE table allows calculation of all species’ equilibrium concentrations:

\(\left[{\text{Ag}}^{+}\right]\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}0+x=1.1\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}M\)
\(\left[{\text{NH}}_{3}\right]=0+2x=2.2\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}M\)
\(\left[\text{Ag}{\left({\text{NH}}_{3}\right)}_{2}{}^{+}\right]=0.10-x=0.10-0.0011=0.099\)

The concentration of free silver ion in the solution is 0.0011 M.

Check Your Learning Calculate the silver ion concentration, [Ag+], of a solution prepared by dissolving 1.00 g of AgNO3 and 10.0 g of KCN in sufficient water to make 1.00 L of solution. (Hint: Because Kf is very large, assume the reaction goes to completion then calculate the [Ag+] produced by dissociation of the complex.)

Answer:

2.5 \(×\) 10–22M

Key Concepts and Summary

A Lewis acid is a species that can accept an electron pair, whereas a Lewis base has an electron pair available for donation to a Lewis acid. Complex ions are examples of Lewis acid-base adducts and comprise central metal atoms or ions acting as Lewis acids bonded to molecules or ions called ligands that act as Lewis bases. The equilibrium constant for the reaction between a metal ion and ligands produces a complex ion called a formation constant; for the reverse reaction, it is called a dissociation constant.

Chemistry End of Chapter Exercises

Even though Ca(OH)2 is an inexpensive base, its limited solubility restricts its use. What is the pH of a saturated solution of Ca(OH)2?

Under what circumstances, if any, does a sample of solid AgCl completely dissolve in pure water?

when the amount of solid is so small that a saturated solution is not produced

Explain why the addition of NH3 or HNO3 to a saturated solution of Ag2CO3 in contact with solid Ag2CO3 increases the solubility of the solid.

Calculate the cadmium ion concentration, [Cd2+], in a solution prepared by mixing 0.100 L of 0.0100 M Cd(NO3)2 with 1.150 L of 0.100 NH3(aq).

8 \(×\) 10–5M

Explain why addition of NH3 or HNO3 to a saturated solution of Cu(OH)2 in contact with solid Cu(OH)2 increases the solubility of the solid.

Sometimes equilibria for complex ions are described in terms of dissociation constants, Kd. For the complex ion \({\text{AlF}}_{6}{}^{\text{3−}}\) the dissociation reaction is:

\({\text{AlF}}_{6}{}^{\text{3−}}⇌{\text{Al}}^{\text{3+}}+6{\text{F}}^{\text{−}}\) and \({K}_{\text{d}}=\frac{\left[{\text{Al}}^{\text{3+}}\right]{\left[{\text{F}}^{\text{−}}\right]}^{6}}{\left[{\text{AlF}}_{6}{}^{\text{3−}}\right]}=2\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-24}\)

Calculate the value of the formation constant, Kf, for \({\text{AlF}}_{\text{6}}{}^{\text{3−}}.\)

5 \(×\) 1023

Using the value of the formation constant for the complex ion \(\text{Co}{\left({\text{NH}}_{3}\right)}_{6}{}^{\text{2+}},\) calculate the dissociation constant.

Using the dissociation constant, Kd = 7.8 \(×\) 10–18, calculate the equilibrium concentrations of Cd2+ and CN– in a 0.250-M solution of \(\text{Cd}{\left(\text{CN}\right)}_{4}{}^{\text{2−}}.\)

This table has two main columns and three rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ) and Equilibrium ( M ). The second column has the header, “[ C d ( C N ) subscript 4 to the second power superscript negative sign ] [ C N superscript negative sign ] [ C d to the second power superscript positive sign ].” Under the second column is a subgroup of two rows and three columns. The first column contains the following: 0.250 and 0.250 minus x. The second column contains the following: 0 and 4 x. The third column contains the following: 0 and x.


 [Cd2+] = 9.5 \(×\) 10–5M; [CN–] = 3.8 \(×\) 10–4M

Using the dissociation constant, Kd = 3.4 \(×\) 10–15, calculate the equilibrium concentrations of Zn2+ and OH– in a 0.0465-M solution of \(\text{Zn}{\left(\text{OH}\right)}_{4}{}^{\text{2−}}.\)

Using the dissociation constant, Kd = 2.2 \(×\) 10–34, calculate the equilibrium concentrations of Co3+ and NH3 in a 0.500-M solution of \(\text{Co}{\left({\text{NH}}_{3}\right)}_{6}{}^{\text{3+}}.\)

[Co3+] = 3.0 \(×\) 10–6M; [NH3] = 1.8 \(×\) 10–5M

Using the dissociation constant, Kd = 1 \(×\) 10–44, calculate the equilibrium concentrations of Fe3+ and CN– in a 0.333 M solution of \(\text{Fe}{\left(\text{CN}\right)}_{6}{}^{\text{3−}}.\)

Calculate the mass of potassium cyanide ion that must be added to 100 mL of solution to dissolve 2.0 \(×\) 10–2 mol of silver cyanide, AgCN.

1.3 g

Calculate the minimum concentration of ammonia needed in 1.0 L of solution to dissolve 3.0 \(×\) 10–3 mol of silver bromide.

A roll of 35-mm black and white photographic film contains about 0.27 g of unexposed AgBr before developing. What mass of Na2S2O3·5H2O (sodium thiosulfate pentahydrate or hypo) in 1.0 L of developer is required to dissolve the AgBr as \(\text{Ag}{\left({\text{S}}_{2}{\text{O}}_{3}\right)}_{2}{}^{\text{3−}}\) (Kf = 4.7 \(×\) 1013)?

0.79 g

We have seen an introductory definition of an acid: An acid is a compound that reacts with water and increases the amount of hydronium ion present. In the chapter on acids and bases, we saw two more definitions of acids: a compound that donates a proton (a hydrogen ion, H+) to another compound is called a Brønsted-Lowry acid, and a Lewis acid is any species that can accept a pair of electrons. Explain why the introductory definition is a macroscopic definition, while the Brønsted-Lowry definition and the Lewis definition are microscopic definitions.

Write the Lewis structures of the reactants and product of each of the following equations, and identify the Lewis acid and the Lewis base in each:

(a) \({\text{CO}}_{2}+{\text{OH}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{HCO}}_{3}{}^{\text{−}}\)

(b) \(\text{B}{\left(\text{OH}\right)}_{3}+{\text{OH}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{B}{\left(\text{OH}\right)}_{4}{}^{\text{−}}\)

(c) \({\text{I}}^{\text{−}}+{\text{I}}_{2}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{I}}_{3}{}^{\text{−}}\)

(d) \({\text{AlCl}}_{3}+{\text{Cl}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{AlCl}}_{4}{}^{\text{−}}\) (use Al-Cl single bonds)

(e) \({\text{O}}^{\text{2−}}+{\text{SO}}_{3}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{SO}}_{4}{}^{\text{2−}}\)

(a)

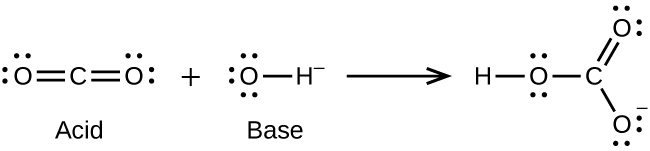
This figure shows a chemical reaction modeled with structural formulas. On the left side is a structure with a central C atom. O atoms, each with two unshared electron pairs, are double bonded to the left and right sides of the C atom. Following a plus sign is another structure in brackets which has an O atom with three unshared electron dot pairs single bonded to an H atom on the right. Outside the brackets is superscript negative sign. Following a right pointing arrow is a structure in brackets that has a central C atom to which 3 O atoms are bonded. Above and slightly to the right, one of the O atoms is connected with a double bond. This O atom has two unshared electron pairs. The second O atom is single bonded below and slightly to the right. This O atom has three unshared electron pairs. The third O atom is bonded to the left of the C atom. This O atom has two unshared electron pairs and an H atom single bonded to its left. Outside the brackets to the right is a superscript negative symbol.


 (b)

This figure shows a chemical reaction modeled with structural formulas. On the left side is a structure that has a central B atom to which 3 O atoms are bonded. The O atoms above and below slightly right of the B atom each have an H atom single bonded to the right. The third O atom is single bonded to the left side of the B atom. This O atom has an H atom single bonded to its left side. All O atoms in this structure have two unshared electron pairs. Following a plus sign is another structure which has an O atom single bonded to an H atom on its right. The O atom has three unshared electron pairs. The structure appears in brackets with a superscript negative sign. Following a right pointing arrow is a structure in brackets has a central B atom to which 4 O atoms are bonded. The O atoms above, below, and right of the B atom each hav an H atom single bonded to the right. The third O atom is single bonded to the left side of the B atom. This O atom has an H atom single bonded to its left side. All O atoms in this structure have two unshared electron pairs. Outside the brackets to the right is a superscript negative symbol.


 (c)

This figure illustrates a chemical reaction using structural formulas. On the left, two I atoms, each with 3 unshared electron pairs, are joined with a single bond. Following a plus sign is another structure which has an I atom with four pairs of electron dots and a superscript negative sign. Following a right pointing arrow is a structure in brackets that has three I atoms connected in a line with single bonds. The two end I atoms have three unshared electron dot pairs and the I atom at the center has two unshared electron pairs. Outside the brackets is a superscript negative sign.


 (d)

This figure illustrates a chemical reaction using structural formulas. On the left, an A l atom is positioned at the center of a structure and three Cl atoms are single bonded above, left, and below. Each C l atom has three pairs of electron dots. Following a plus sign is another structure which has an F atom is surrounded by four electron dot pairs and a superscript negative symbol. Following a right pointing arrow is a structure in brackets that has a central A l atom to which 4 C l atoms are connected with single bonds above, below, to the left, and to the right. Each C l atom in this structure has three pairs of electron dots. Outside the brackets is a superscript negative symbol.


 (e)

This figure illustrates a chemical reaction using structural formulas. On the left is a structure which has an S atom at the center. O atoms are single bonded above and below. These O atoms have three electron dot pairs each. To the right of the S atom is a double bonded O atom which has two pairs of electron dots. Following a plus sign is an O atom which is surrounded by four electron dot pairs and has a superscript 2 negative. Following a right pointing arrow is a structure in brackets that has a central S atom to which 4 O atoms are connected with single bonds above, below, to the left, and to the right. Each of the O atoms has three pairs of electron dots. Outside the brackets is a superscript 2 negative.

Write the Lewis structures of the reactants and product of each of the following equations, and identify the Lewis acid and the Lewis base in each:

(a) \({\text{CS}}_{2}+{\text{SH}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{HCS}}_{3}{}^{\text{−}}\)

(b) \({\text{BF}}_{3}+{\text{F}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{BF}}_{4}{}^{\text{−}}\)

(c) \({\text{I}}^{\text{−}}+{\text{SnI}}_{2}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{SnI}}_{3}{}^{\text{−}}\)

(d) \(\text{Al}{\left(\text{OH}\right)}_{3}+{\text{OH}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{Al}{\left(\text{OH}\right)}_{4}{}^{\text{−}}\)

(e) \({\text{F}}^{\text{−}}+{\text{SO}}_{3}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{SFO}}_{3}{}^{\text{−}}\)

Using Lewis structures, write balanced equations for the following reactions:

(a) \(\text{HCl}\left(g\right)+{\text{PH}}_{3}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\)

(b) \({\text{H}}_{3}{\text{O}}^{+}+{\text{CH}}_{3}{}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\)

(c) \(\text{CaO}+{\text{SO}}_{3}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\)

(d) \({\text{NH}}_{4}{}^{+}+{\text{C}}_{2}{\text{H}}_{5}{\text{O}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\)

(a)

This figure represents a chemical reaction in two rows. The top row shows the reaction using chemical formulas. The second row uses structural formulas to represent the reaction. The first row contains the equation H C l ( g ) plus P H subscript 3 ( g ) right pointing arrow left bracket P H subscript 4 right bracket superscript plus plus left bracket C l with 4 pairs of electron dots right bracket superscript negative sign. The second row begins on the left with H left bracket C l with four unshared electron pairs right bracket plus a structure in brackets with a central P atom with H atoms single bonded at the left, above, and to the right. A single unshared electron pair is on the central P atom. Outside the brackets to the right is a superscript plus sign. Following a right pointing arrow is a structure in brackets with a central P atom with H atoms single bonded at the left, above, below, and to the right. Outside the brackets is a superscript plus sign. This structure is followed by a plus and a C l atom in brackets with four unshared electron pairs and a superscript negative sign.


 (b) \({\text{H}}_{3}{\text{O}}^{+}+{\text{CH}}_{3}{}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{CH}}_{4}+{\text{H}}_{2}\text{O}\)

This figure represents a chemical reaction using structural formulas. A structure is shown in brackets on the left which is composed of a central O atom with one unshared electron pair and three single bonded H atoms to the left, right, and above the atom. Outside the brackets to the right is a superscript plus sign. Following a plus sign, is another structure in brackets composed of a central C atom with one unshared electron pair and three single bonded H atoms to the left, right, and above the atom. Outside the brackets to the right is a superscript negative sign. Following a right pointing arrow is a structure with a central C atom with H atoms single bonded above, below, left and right. Following a plus sign is a structure with a central O atom with two unshared electron pairs and two H atoms connected with single bonds.


 (c) \(\text{CaO}+{\text{SO}}_{3}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{CaSO}4\)

This figure represents a chemical reaction using structural formulas. On the left, C a superscript 2 plus is just left of bracket O with four unshared electron pairs right bracket superscript 2 negative plus a structure with a central S atom to which two O atoms are single bonded at the left and right, and a single O atom is double bonded above. The two single bonded O atoms each have three unshared electron pairs and the double bonded O atom has two unshared electron pairs. Following a right pointing arrow is C a superscript 2 plus just left of a structure in brackets with a central S atom which has 4 O atoms single bonded at the left, above, below, and to the right. Each of the O atoms has three unshared electron pairs. Outside the brackets to the right is a superscript two negative.


 (d) \({\text{NH}}_{4}{}^{+}+{\text{C}}_{2}{\text{H}}_{5}{\text{O}}^{\text{−}}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{C}}_{2}{\text{H}}_{5}\text{OH}+{\text{NH}}_{3}\)

This figure represents a chemical reaction using structural formulas. A structure is shown in brackets on the left which is composed of a central N atom with four single bonded H atoms to the left, right, above, and below the atom. Outside the brackets to the right is a superscript plus sign. Following a plus sign, is another structure in brackets composed of a C atom with three single bonded H atoms above, below, and to the left. A second C atom is single bonded to the right. This C atom has H atoms single bonded above and below. To the right of the second C atom, an O atom is single bonded. This O atom has three unshared electron pairs. Outside the brackets to the right is a subperscript negative. Following a right pointing arrow is a structure composed of a C atom with three single bonded H atoms above, below, and to the left. A second C atom is single bonded to the right. This C atom has H atoms single bonded above and below. To the right of the second C atom, an O atom is single bonded. This O atom has two unshared electron pairs and an H atom single bonded to its right.

Calculate \(\left[{\text{HgCl}}_{4}{}^{\text{2−}}\right]\) in a solution prepared by adding 0.0200 mol of NaCl to 0.250 L of a 0.100-M HgCl2 solution.

In a titration of cyanide ion, 28.72 mL of 0.0100 M AgNO3 is added before precipitation begins. [The reaction of Ag+ with CN– goes to completion, producing the \(\text{Ag}{\left(\text{CN}\right)}_{2}{}^{\text{−}}\) complex.] Precipitation of solid AgCN takes place when excess Ag+ is added to the solution, above the amount needed to complete the formation of \(\text{Ag}{\left(\text{CN}\right)}_{2}{}^{\text{−}}.\) How many grams of NaCN were in the original sample?

0.0281 g

What are the concentrations of Ag+, CN–, and \(\text{Ag}{\left(\text{CN}\right)}_{2}{}^{\text{−}}\) in a saturated solution of AgCN?

In dilute aqueous solution HF acts as a weak acid. However, pure liquid HF (boiling point = 19.5 °C) is a strong acid. In liquid HF, HNO3 acts like a base and accepts protons. The acidity of liquid HF can be increased by adding one of several inorganic fluorides that are Lewis acids and accept F– ion (for example, BF3 or SbF5). Write balanced chemical equations for the reaction of pure HNO3 with pure HF and of pure HF with BF3.

\({\text{HNO}}_{3}\left(l\right)+\text{HF}\left(l\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{2}{\text{NO}}_{3}{}^{+}+{\text{F}}^{\text{−}};\)\(\text{HF}\left(l\right)+{\text{BF}}_{3}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}^{+}+{\text{BF}}_{4}\)

The simplest amino acid is glycine, H2NCH2CO2H. The common feature of amino acids is that they contain the functional groups: an amine group, –NH2, and a carboxylic acid group, –CO2H. An amino acid can function as either an acid or a base. For glycine, the acid strength of the carboxyl group is about the same as that of acetic acid, CH3CO2H, and the base strength of the amino group is slightly greater than that of ammonia, NH3.

(a) Write the Lewis structures of the ions that form when glycine is dissolved in 1 M HCl and in 1 M KOH.

(b) Write the Lewis structure of glycine when this amino acid is dissolved in water. (Hint: Consider the relative base strengths of the –NH2 and \(-{\text{CO}}_{2}{}^{\text{−}}\) groups.)

Boric acid, H3BO3, is not a Brønsted-Lowry acid but a Lewis acid.

(a) Write an equation for its reaction with water.

(b) Predict the shape of the anion thus formed.

(c) What is the hybridization on the boron consistent with the shape you have predicted?

(a) \({\text{H}}_{3}{\text{BO}}_{3}+{\text{H}}_{2}\text{O}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{4}{\text{BO}}_{4}{}^{\text{−}}+{\text{H}}^{+};\) (b) The electronic and molecular shapes are the same—both tetrahedral. (c) The tetrahedral structure is consistent with sp3 hybridization.

Glossary

complex ion
ion consisting of a central atom surrounding molecules or ions called ligands via coordinate covalent bonds
coordinate covalent bond
(also, dative bond) covalent bond in which both electrons originated from the same atom
dissociation constant
(Kd) equilibrium constant for the decomposition of a complex ion into its components
formation constant
(Kf) (also, stability constant) equilibrium constant for the formation of a complex ion from its components
Lewis acid
any species that can accept a pair of electrons and form a coordinate covalent bond
Lewis acid-base adduct
compound or ion that contains a coordinate covalent bond between a Lewis acid and a Lewis base
Lewis acid-base chemistry
reactions involving the formation of coordinate covalent bonds
Lewis base
any species that can donate a pair of electrons and form a coordinate covalent bond
ligand
molecule or ion acting as a Lewis base in complex ion formation; bonds to the central atom of the complex

License

Icon for the Creative Commons Attribution 4.0 International License

Lewis Acids and Bases Copyright © by Paul Flowers; Edward J. Neth; William R. Robinson; Klaus Theopold; and Richard Langley is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book