218 Nuclear Equations

Types of Particles in Nuclear Reactions

Many entities can be involved in nuclear reactions. The most common are protons, neutrons, alpha particles, beta particles, positrons, and gamma rays, as shown in (Figure). Protons \(\left({}_{1}^{1}\text{p},\) also represented by the symbol \({}_{1}^{1}\text{H}\right)\) and neutrons \(\left({}_{0}^{1}\text{n}\right)\) are the constituents of atomic nuclei, and have been described previously. Alpha particles \(\left({}_{2}^{4}\text{He},\) also represented by the symbol \({}_{2}^{4}\text{α}\right)\) are high-energy helium nuclei. Beta particles \(\left({}_{-1}^{\phantom{\rule{0.5em}{0ex}}0}\text{β},\) also represented by the symbol \({}_{-1}^{\phantom{\rule{0.5em}{0ex}}0}\text{e}\right)\) are high-energy electrons, and gamma rays are photons of very high-energy electromagnetic radiation. Positrons \(\left({}_{+1}^{\phantom{\rule{0.5em}{0ex}}0}\text{e},\) also represented by the symbol \({}_{+1}^{\phantom{\rule{0.5em}{0ex}}0}\text{β}\right)\) are positively charged electrons (“anti-electrons”). The subscripts and superscripts are necessary for balancing nuclear equations, but are usually optional in other circumstances. For example, an alpha particle is a helium nucleus (He) with a charge of +2 and a mass number of 4, so it is symbolized \({}_{2}^{4}\text{He}.\) This works because, in general, the ion charge is not important in the balancing of nuclear equations.

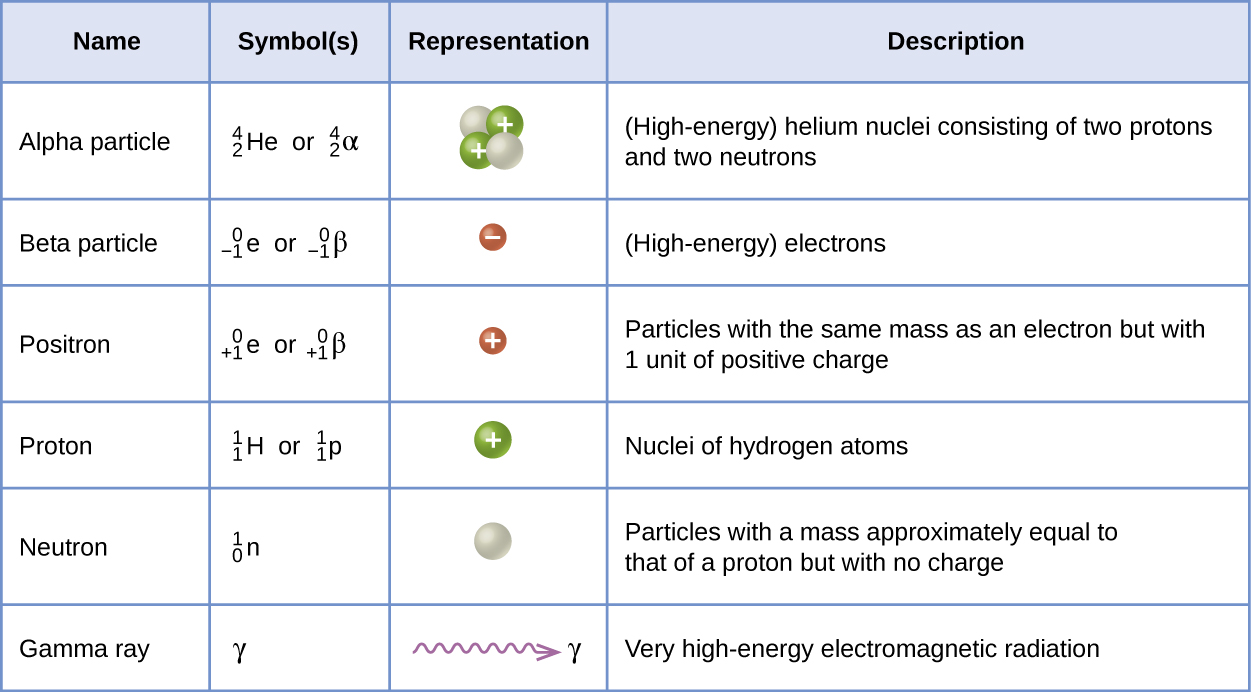
Note that positrons are exactly like electrons, except they have the opposite charge. They are the most common example of antimatter, particles with the same mass but the opposite state of another property (for example, charge) than ordinary matter. When antimatter encounters ordinary matter, both are annihilated and their mass is converted into energy in the form of gamma rays (γ)—and other much smaller subnuclear particles, which are beyond the scope of this chapter—according to the mass-energy equivalence equation E = mc², seen in the preceding section. For example, when a positron and an electron collide, both are annihilated and two gamma ray photons are created:

As seen in the chapter discussing light and electromagnetic radiation, gamma rays compose short wavelength, high-energy electromagnetic radiation and are (much) more energetic than better-known X-rays that can behave as particles in the wave-particle duality sense. Gamma rays are a type of high energy electromagnetic radiation produced when a nucleus undergoes a transition from a higher to a lower energy state, similar to how a photon is produced by an electronic transition from a higher to a lower energy level. Due to the much larger energy differences between nuclear energy shells, gamma rays emanating from a nucleus have energies that are typically millions of times larger than electromagnetic radiation emanating from electronic transitions.

Balancing Nuclear Reactions

A balanced chemical reaction equation reflects the fact that during a chemical reaction, bonds break and form, and atoms are rearranged, but the total numbers of atoms of each element are conserved and do not change. A balanced nuclear reaction equation indicates that there is a rearrangement during a nuclear reaction, but of nucleons (subatomic particles within the atoms’ nuclei) rather than atoms. Nuclear reactions also follow conservation laws, and they are balanced in two ways:

1. The sum of the mass numbers of the reactants equals the sum of the mass numbers of the products.
2. The sum of the charges of the reactants equals the sum of the charges of the products.

If the atomic number and the mass number of all but one of the particles in a nuclear reaction are known, we can identify the particle by balancing the reaction. For instance, we could determine that \({}_{\phantom{\rule{0.5em}{0ex}}8}^{17}\text{O}\) is a product of the nuclear reaction of \({}_{\phantom{\rule{0.5em}{0ex}}7}^{14}\text{N}\) and \({}_{2}^{4}\text{He}\) if we knew that a proton, \({}_{1}^{1}\text{H},\) was one of the two products. (Figure) shows how we can identify a nuclide by balancing the nuclear reaction.

Following are the equations of several nuclear reactions that have important roles in the history of nuclear chemistry:

• The first naturally occurring unstable element that was isolated, polonium, was discovered by the Polish scientist Marie Curie and her husband Pierre in 1898. It decays, emitting α particles:
  
  \({}_{\phantom{\rule{0.5em}{0ex}}84}^{212}\text{Po}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{}_{\phantom{\rule{0.5em}{0ex}}82}^{208}\text{Pb}+{}_{2}^{4}\text{He}\)
• The first nuclide to be prepared by artificial means was an isotope of oxygen, ¹⁷O. It was made by Ernest Rutherford in 1919 by bombarding nitrogen atoms with α particles:
  
  \({}_{\phantom{\rule{0.5em}{0ex}}7}^{14}\text{N}+{}_{2}^{4}\text{He}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{}_{\phantom{\rule{0.5em}{0ex}}8}^{17}\text{O}+{}_{1}^{1}\text{H}\)
• James Chadwick discovered the neutron in 1932, as a previously unknown neutral particle produced along with ¹²C by the nuclear reaction between ⁹Be and ⁴He:
  
  \({}_{4}^{9}\text{Be}+{}_{2}^{4}\text{He}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{}_{\phantom{\rule{0.5em}{0ex}}6}^{12}\text{C}+{}_{0}^{1}\text{n}\)
• The first element to be prepared that does not occur naturally on the earth, technetium, was created by bombardment of molybdenum by deuterons (heavy hydrogen, \({}_{1}^{2}\text{H}\right)\), by Emilio Segre and Carlo Perrier in 1937:
  
  \({}_{1}^{2}\text{H}+{}_{42}^{97}\text{Mo}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}2{}_{0}^{1}\text{n}+{}_{43}^{97}\text{Tc}\)
• The first controlled nuclear chain reaction was carried out in a reactor at the University of Chicago in 1942. One of the many reactions involved was:
  
  \({}_{\phantom{\rule{0.5em}{0ex}}92}^{235}\text{U}+{}_{0}^{1}\text{n}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{}_{35}^{87}\text{Br}+{}_{\phantom{\rule{0.5em}{0ex}}57}^{146}\text{La}+3{}_{0}^{1}\text{n}\)