"

Chapter 4: The Integral

Chapter 4 Review Problems

Chapter 3 Review Problems

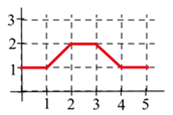
  1. Let  A(x) represent the area bounded by the graph and the horizontal axis and vertical lines at t=0 and t=x  for the graph in Fig. 1.  Evaluate  A(x)  for  x = 1, 2, 3, 4, and 5.
Graph of a piecewise linear function. The x-axis goes from 0 to 5, and the y-axis from 0 to 3. The function starts at (1,1), rises to (2,2), stays constant to (3,2), drops to (4,1), and remains constant to (5,1).
Fig. 1
  1. Let  B(x) represent the area bounded by the graph and the horizontal axis and vertical lines at t=0 and  t=x  for the graph in Fig. 2.  Evaluate  B(x)  for  x = 1, 2, 3, 4, and 5.

Graph of a piecewise linear function with a blue line. The x-axis ranges from 0 to 5, and the y-axis from 0 to 3. The function starts at (1,2), drops to (2,1), stays constant at y=1 until x=3, rises to (4,2), and then drops to (5,0).
Fig. 2

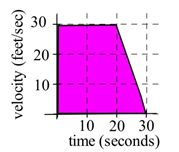
3. A car had the velocity shown in Fig. 3.  How far did the car travel from t= 0 to t = 30 seconds?

Graph of velocity (in feet per second) versus time (in seconds). The x-axis ranges from 0 to 35 seconds, and the y-axis from 0 to 35 feet per second. The graph forms a trapezoid: it starts at (0,10), rises to (10,30), stays constant until (20,30), then decreases to (30,0). The area under the curve is shaded in pink.
Fig. 3

4. The velocities of two cars are shown in Fig. 4.  

(a)  From the time the brakes were applied, how many seconds did it take each car to stop?  

(b)  From the time the brakes were applied, which car traveled farther until it came to a complete stop?

Graph of velocity (in feet per second) versus time (in seconds). The y-axis ranges from 0 to 80 feet/sec, and the x-axis from 0 to 60 seconds. Line A (red) starts at 80 feet/sec, stays constant until 20 seconds, then decreases linearly to 0 at 40 seconds. Line B (blue) starts at 40 feet/sec, stays constant until 20 seconds, then decreases linearly to -20 feet/sec at 60 seconds.
Fig. 4

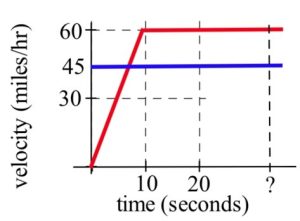
5.  Police chase:  A speeder traveling 45 miles per hour (in a 25 mph zone) passes a stopped police car which immediately takes off after the speeder.  If the police car speeds up steadily to 60 miles/hour in 20 seconds and then travels at a steady 60 miles/hour, how long and how far before the police car catches the speeder who continued traveling at 45 miles/hour?  (Fig. 5)

Fig. 5

In problems  6 – 8 , represent the area of each bounded region as a definite integral, and use geometry to determine the value of the definite integral.

6. The region bounded by  y = 4 – 2x , the x–axis, and the y–axis.

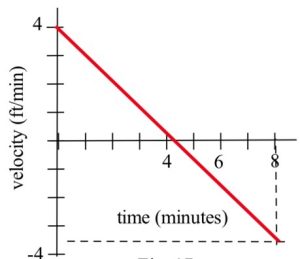
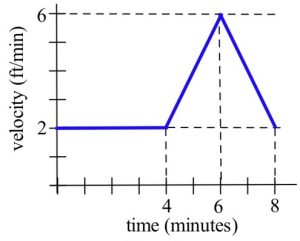
7. Your velocity along a straight road is shown in Fig. 6. How far did you travel in 8 minutes?

Graph of velocity (in feet per minute) versus time (in minutes). The x-axis ranges from 0 to 8 minutes, and the y-axis from -4 to 4 feet per minute. A red line starts at (0, 4) and decreases linearly to (8, -4).
Fig 6.

8. Your velocity along a straight road is shown in Fig. 7. How many feet did you walk in 8 minutes?

The image shows a graph of velocity versus time. The x-axis represents time in minutes, ranging from 0 to 8 minutes, and the y-axis represents velocity in feet per minute (ft/min), ranging from 0 to 6 ft/min. The graph is a piecewise linear function with three segments: From time 0 to 4 minutes, the velocity is constant at 2 ft/min. From time 4 to 6 minutes, the velocity increases linearly from 2 ft/min to a peak of 6 ft/min. From time 6 to 8 minutes, the velocity decreases linearly back down to 2 ft/min. This graph helps illustrate how an object's speed changes over time.
Fig. 7

Media Attributions

  • Fig 33.JPG
  • Fig 34
  • Fig 37
  • Fig 39
  • Fig 41
  • Fig 46
  • Fig 47

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Applied Calculus Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book