Chapter 1: Algebra Review

Section 1.8: Logarithmic Functions

Learning Objectives

By the end of this section, the student should be able to:

  • Convert from logarithmic to exponential form.
  • Convert from exponential to logarithmic form.
  • Evaluate logarithms.
  • Use common logarithms.
  • Use natural logarithms.

 

Logarithm Basics

Logarithms are the inverse of exponential functions – they allow us to undo exponential functions and solve for the exponent. They are also commonly used to express quantities that vary widely in size.

Logarithm Equivalent to an Exponential

The logarithm (base [latex]b[/latex]) function, written [latex]\log_b (x)[/latex], is the inverse of the exponential function (base [latex]b[/latex]), [latex]b^x[/latex].

This means the statement [latex]b^a=c[/latex] is equivalent to the statement [latex]\log_b (c)=a[/latex].

 

Properties of Logs: Inverse Properties

  • [latex]\log_b(b^x)=x[/latex]
  • [latex]b^{\log_b(x)}=x[/latex]

 

Video


 

Example 1

Write these exponential equations as logarithmic equations:

  1. [latex]2^3=8[/latex]
  2. [latex]5^2=25[/latex]
  3. [latex]10^{-4}=\frac{1}{10000}[/latex]
  4. [latex]2^3=8[/latex] is equivalent to [latex]\log_2(8)=3[/latex].
  5. [latex]5^2=25[/latex] is equivalent to [latex]\log_5(25)=2[/latex].
  6. [latex]10^{-4}=\frac{1}{10000}[/latex] is equivalent to [latex]\log_{10}\left(\frac{1}{10000}\right)=-4[/latex].

 

Example 2

Solve [latex]2^x=10[/latex] for [latex]x[/latex].

By rewriting this expression as a logarithm, we get [latex]x=\log_2(10)[/latex].

 

Video

 

While this does define a solution, and an exact solution at that, you may find it somewhat unsatisfying, since it is difficult to compare this expression to the decimal estimate we made earlier. Also, giving an exact expression for a solution is not always useful–often we really need a decimal approximation to the solution. Luckily, this is a task calculators and computers are quite adept at. Unluckily for us, most calculators and computers will only evaluate logarithms of two bases. Happily, this ends up not being a problem, as we’ll see briefly.

Properties of Logs: Inverse Properties

The common log is the logarithm with base 10 and is typically written [latex]\log(x)[/latex].

The natural log is the logarithm with base [latex]e[/latex] and is typically written [latex]\ln(x)[/latex].

 

Example 3

Evaluate [latex]\log(1000)[/latex] using the definition of the common log.

To evaluate [latex]\log(1000)[/latex], we can say [latex]x=\log(1000)[/latex], then rewrite into exponential form using the common log base of 10:[latex]10^x=1000.[/latex]

From this, we might recognize that 1000 is the cube of 10, so [latex]x = 3[/latex].

We also can use the inverse property of logs to write [latex]log_{10}\left(10^3\right) =3[/latex].

Values of the common [latex]log[/latex]
Number Number as exponential log(number)
[latex]1000[/latex] [latex]10^3[/latex] [latex]3[/latex]
[latex]100[/latex] [latex]10^2[/latex] [latex]2[/latex]
[latex]10[/latex] [latex]10^1[/latex] [latex]1[/latex]
[latex]1[/latex] [latex]10^0[/latex] [latex]0[/latex]
[latex]0.1[/latex] [latex]10^{-1}[/latex] [latex]-1[/latex]
[latex]0.01[/latex] [latex]10^{-2}[/latex] [latex]-2[/latex]
[latex]0.001[/latex] [latex]10^{-3}[/latex] [latex]-3[/latex]

 

Example 4

Evaluate [latex]\log(500)[/latex] using your calculator or computer.

Using a computer or calculator, we can evaluate and find that [latex]\log(500)\approx 2.69897[/latex].

 

Another property provides the basis for solving exponential equations.

Properties of Logs: Exponential Property

[latex]\log_b\left(A^r\right)=r\,\log_b(A)[/latex]

 

Solving Exponential Equations

  1. Isolate the exponential expressions when possible.
  2. Take the logarithm of both sides.
  3. Utilize the exponent property for logarithms to pull the variable out of the exponent.
  4. Use algebra to solve for the variable.

 

Video

 

Example 5

In the last section, we predicted the population (in billions) of India [latex]t[/latex] years after [latex]2008[/latex] by using the function [latex]f(t)=1.14(1+0.0134)^t[/latex]. If the population continues following this trend, when will the population reach [latex]2[/latex] billion?

We need to solve for the [latex]t[/latex] so that [latex]f(t) = 2[/latex].

[latex]2=1.14(1.0134)^t[/latex] Initial equation.
[latex]\dfrac{2}{1.14}=1.0134^t[/latex] Divide by 1.14 to isolate the exponential expression.
[latex]\ln\left(\dfrac{2}{1.14}\right)=\ln\left(1.0134^t\right)[/latex] Take the logarithm of both sides of the equation.
[latex]\ln\left(\dfrac{2}{1.14}\right)=t\,\ln(1.0134)[/latex] Apply the exponent property on the right side.
[latex]t = \dfrac{\ln\left(\dfrac{2}{1.14}\right)}{\ln(1.0134)}[/latex] Divide both sides by [latex]\ln(1.0134)[/latex]
[latex]t\approx 42.23 \text{ years}[/latex]

If this growth rate continues, the model predicts the population of India will reach [latex]2[/latex] billion about [latex]42[/latex] years after [latex]2008[/latex], or approximately in the year [latex]2050[/latex].

Example 6

Solve [latex]5e^{-0.3t}=2[/latex] for [latex]t[/latex].

First we divide by 5 to isolate the exponential: [latex]e^{-0.3t}=\frac{2}{5}.[/latex]

Since this equation involves [latex]e[/latex], it makes sense to use the natural log:

[latex]\ln\left(e^{-0.3t}\right)=\ln\left(\dfrac{2}{5}\right)[/latex] Taking the natural log of both sides.
[latex]-0.3t=\ln\left(\dfrac{2}{5}\right)[/latex] Utilizing the inverse property for logs.
[latex]t = \dfrac{\ln\left(\dfrac{2}{5}\right)}{-0.3}[/latex] Now dividing by -0.3.
[latex]t\approx 3.054[/latex]

 

In addition to solving exponential equations, logarithmic expressions are common in many physical situations.

Example 7

In chemistry, [latex]pH[/latex] is a measure of the acidity or basicity of a liquid. The [latex]pH[/latex] is related to the concentration of hydrogen ions, [latex]\left[H^+\right][/latex], measured in moles per liter, by the equation[latex]\text{pH}=-\log\left(\left[H^+\right]\right).[/latex]

If a liquid has concentration of [latex]0.0001[/latex] moles per liter, determine the [latex]pH[/latex]. Determine the hydrogen ion concentration of a liquid with [latex]pH[/latex] of [latex]7[/latex].

To answer the first question, we evaluate the expression [latex]-\log(0.0001)[/latex]. While we could use our calculators for this, we do not really need them here, since we can use the inverse property of logs: [latex]-\log(0.0001)=-\log\left(10^{-4}\right)=-(-4)=4.[/latex]

To answer the second question, we need to solve the equation [latex]7=-\log\left(\left[H^+\right]\right)[/latex]. Begin by isolating the logarithm on one side of the equation by multiplying both sides by -1: [latex]-7=\log\left(\left[H^+\right]\right)[/latex]. Rewriting into exponential form yields the answer: [latex]\left[H^+\right]=10^{-7}=0.0000001\text{ moles per liter}.[/latex]

 

Logarithm Graphs

While we don’t often need to sketch the graph of a logarithm, it is helpful to understand the basic shape.

Graphical Features of the Logarithm

Graphically, given the function [latex]g(x)=\log_b(x)[/latex].

  • The graph has a horizontal intercept at (1, 0).
  • The graph has a vertical asymptote at [latex]x = 0[/latex].
  • The graph is increasing and concave down.
  • The domain of the function is [latex]x \gt 0[/latex], or [latex](0, \infty)[/latex] in interval notation.
  • The range of the function is all real numbers, or [latex](-\infty, \infty)[/latex] in interval notation.

 

When sketching a general logarithm with base [latex]b[/latex], it can be helpful to remember that the graph will pass through the points [latex]\left(\frac{1}{b}, -1\right)[/latex], [latex](1, 0)[/latex], and [latex](b, 1)[/latex].

To get a feeling for how the base affects the shape of the graph, examine the graphs below:

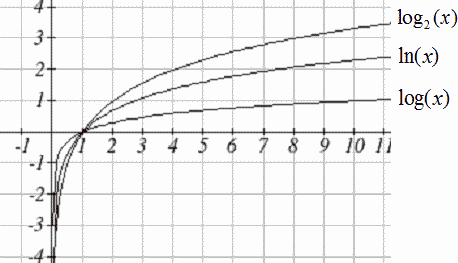
Another important observation made was the domain of the logarithm: [latex]x \gt 0[/latex]. Like the reciprocal and square root functions, the logarithm has a restricted domain that must be considered when finding the domain of a composition involving a log.

Example 8

Find the domain of the function [latex]f(x)=\log(5-2x)[/latex].

The logarithm is only defined when the input is positive, so this function will only be defined when [latex]5-2x \gt 0[/latex]. Solving this inequality, [latex]-2x \gt -5[/latex], so [latex]x\lt \frac{5}{2}[/latex].

The domain of this function is [latex]x\lt \frac{5}{2}[/latex], or, in interval notation, [latex]\left(-\infty, \frac{5}{2} \right)[/latex].

 

Changing Logarithm Bases

[Content section Introduction from Calculus, Volume 1, by Strang and Herman, OpenStax (Web), licensed under a CC BY-NC-SA 4.0 License.]

When evaluating a logarithmic function with a calculator, you may have noticed that the only options are [latex]\log_{10}[/latex] or log, called the common logarithm, or ln, which is the natural logarithm. However, exponential functions and logarithm functions can be expressed in terms of any desired base [latex]b[/latex]. If you need to use a calculator to evaluate an expression with a different base, you can apply the change-of-base formulas first. Using this change of base, we typically write a given exponential or logarithmic function in terms of the natural exponential and natural logarithmic functions.

Rule: Change-of-Base Formulas

Let [latex]a \lt 0, \, b \lt 0[/latex], and [latex]a\ne 1, \, b\ne 1[/latex].

  1. [latex]a^x=b^{x \log_b a}[/latex] for any real number [latex]x[/latex].
    If [latex]b=e[/latex], this equation reduces to [latex]a^x=e^{x \log_e a}=e^{x \ln a}[/latex].
  2. [latex]\log_a x=\frac{\log_b x}{\log_b a}[/latex] for any real number [latex]x \lt 0[/latex].
    If [latex]b=e[/latex], this equation reduces to [latex]\log_a x=\frac{\ln x}{\ln a}[/latex].

Example 9

Use a calculating utility to evaluate [latex]\log_3 7[/latex] with the change-of-base formula presented earlier.

Solution

Use the second equation with [latex]a=3[/latex] and [latex]e=3[/latex]:

[latex]\log_3 7=\frac{\ln 7}{\ln 3} \approx 1.77124[/latex].

 

Example 10

Use the change-of-base formula and a calculating utility to evaluate [latex]\log_4 6[/latex].

Hint

Use the change of base to rewrite this expression in terms of expressions involving the natural logarithm function.

Solution

1.29248

Chapter Opener: The Richter Scale for Earthquakes

A photograph of an earthquake fault.
Figure 6: (credit: modification of work by Robb Hannawacker, NPS)

From Calculus, Volume 1, by Strang and Herman, OpenStax (Web), licensed under a CC BY-NC-SA 4.0 License.

In 1935, Charles Richter developed a scale (now known as the Richter scale) to measure the magnitude of an earthquake. The scale is a base-10 logarithmic scale, and it can be described as follows: Consider one earthquake with magnitude [latex]R_1[/latex] on the Richter scale and a second earthquake with magnitude [latex]R_2[/latex] on the Richter scale. Suppose [latex]R_1 R_2[/latex], which means the earthquake of magnitude [latex]R_1[/latex] is stronger, but how much stronger is it than the other earthquake? A way of measuring the intensity of an earthquake is by using a seismograph to measure the amplitude of the earthquake waves. If [latex]A_1[/latex] is the amplitude measured for the first earthquake and [latex]A_2[/latex] is the amplitude measured for the second earthquake, then the amplitudes and magnitudes of the two earthquakes satisfy the following equation:

[latex]R_1 - R_2 = \log_{10}(\frac{A_1}{A_2})[/latex].

Consider an earthquake that measures 8 on the Richter scale and an earthquake that measures 7 on the Richter scale. Then,

[latex]8-7=\log_{10}(\frac{A_1}{A_2})[/latex].

Therefore,

[latex]\log_{10}(\frac{A_1}{A_2})=1[/latex],

which implies [latex]A_1 / A_2 = 10[/latex] or [latex]A_1 = 10A_2[/latex]. Since [latex]A_1[/latex] is 10 times the size of [latex]A_2[/latex], we say that the first earthquake is 10 times as intense as the second earthquake. On the other hand, if one earthquake measures 8 on the Richter scale and another measures 6, then the relative intensity of the two earthquakes satisfies the equation

[latex]\log_{10}(\frac{A_1}{A_2})=8-6=2[/latex].

Therefore, [latex]A_1=100A_2[/latex]. That is, the first earthquake is 100 times more intense than the second earthquake.

How can we use logarithmic functions to compare the relative severity of the magnitude 9 earthquake in Japan in 2011 with the magnitude 7.3 earthquake in Haiti in 2010?

Solution

To compare the Japan and Haiti earthquakes, we can use an equation presented earlier:

[latex]9-7.3=\log_{10}(\frac{A_1}{A_2})[/latex].

Therefore, [latex]A_1 / A_2=10^{1.7}[/latex], and we conclude that the earthquake in Japan was approximately 50 times more intense than the earthquake in Haiti.

Compare the relative severity of a magnitude 8.4 earthquake with a magnitude 7.4 earthquake.

Hint

[latex]R_1-R_2=\log_{10}(A_1 / A_2)[/latex].

Solution

The magnitude 8.4 earthquake is roughly 10 times as severe as the magnitude 7.4 earthquake.

Vocabulary

logarithm
natural logarithm
common logarithm
definition

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Applied Calculus Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book