Chapter 3: Applications of the Derivative
Chapter 3 Review Problems
Chapter 3 Review Problems
1.
Where do [latex]f(x) = x^2 – 10x + 3[/latex] and [latex]g(x) = x^3 – 12x[/latex] have horizontal tangent lines ?
2.
[latex]f(x) = x^3 + A x^2 + B x + C[/latex] with constants [latex]A, B[/latex] and [latex]C[/latex]. Can you find conditions on the constants [latex]A[/latex], [latex]B[/latex], and [latex]C[/latex] that will guarantee that the graph of [latex]y = f(x)[/latex] has two distinct “vertices”? (Here a “vertex” means a place where the curve changes from increasing to decreasing or from decreasing to increasing.)
3.
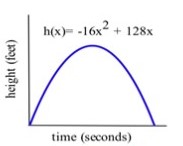
An arrow shot straight up from ground level with an initial velocity of [latex]128[/latex] feet per second will be at the height [latex]h(x) = –16x^2 + 128x[/latex] feet after [latex]x[/latex] seconds. (Fig. 3)
(a) Determine the velocity of the arrow when [latex]x = 0, 1[/latex] and [latex]2[/latex] seconds.
(b) What is the velocity of the arrow, [latex]v(x)[/latex], at any time [latex]x[/latex]?
(c) At what time x will the velocity of the arrow be [latex]0[/latex]?
(d) What is the greatest height the arrow reaches?
(e) How long will the arrow be aloft?
(f) Use the answer for the velocity in part (b) to determine the acceleration, [latex]a(x) = v '(x)[/latex], at any time [latex]x[/latex].
4.
If an arrow is shot straight up from ground level on the moon with an initial velocity of [latex]128[/latex] feet per second, its height will be [latex]h(x) = –2.65x^2 + 128x[/latex] feet at x seconds. Do parts (a)–(f) of problem 31 using this new equation for [latex]h[/latex].
In problems 5–9, differentiate each function and find the equation of the tangent line at [latex]x = a[/latex].
5.
[latex]y = (x^2+2x+2)^{\frac{1}{2}}; a = 0[/latex]
6.
[latex]y = \bigg( 1- \frac{3}{x} \bigg)^4; a= 1[/latex]
7.
[latex]y= \bigg( x + \frac{1}{x} \bigg)^2 ; a = 0.5[/latex]
8.
[latex]y= \frac{5}{3+e^t} ; a = 0[/latex]
9.
[latex]y = e^x + e^{-x} ; a = 0[/latex]
10.
A manufacturer has determined that an employee with d days of production experience will be able to produce approximately [latex]P(d) = 3 + 15( 1 – e^{–0.2d} )[/latex] items per day.
(a) Approximately how many items will a beginning employee be able to produce each day?
(b) How many items will an experienced employee be able to produce each day?
(c) What is the marginal production rate of an employee with 5 days of experience? (What are the units of your answer, and what does this answer mean?)
11.
The air pressure [latex]P(h)[/latex], in pounds per square inch, at an altitude of h feet above sea level is approximately [latex]P(h) = 14.7 e^{–0.0000385h}[/latex].
(a) What is the air pressure at sea level? What is the air pressure at an altitude of [latex]30,000[/latex] feet?
(b) At what altitude is the air pressure [latex]10[/latex] pounds per square inch?
(c) If you are in a balloon that is [latex]2000[/latex] feet above the Pacific Ocean and is rising at [latex]500[/latex] feet per minute, how fast is the air pressure on the balloon changing?
(d) If the temperature of the gas in the balloon remained constant during this ascent, what would happen to the volume of the balloon?
For problems 12–24, calculate [latex]y' = \frac{dy}{dx}[/latex]. The letters A–D represent constants.
12.
[latex]y= Ax^3-B[/latex]
13.
[latex]y= Ax^3+bx^2+C[/latex]
14.
[latex]y= \sqrt{A+Bx^2}[/latex]
15.
[latex]y= \sqrt[3]{A-Bx^3}[/latex]
16.
[latex]y= Ae^{Bx}[/latex]
17.
[latex]y= xe^{Bx}[/latex]
18.
[latex]e^{Ax} + e^{-Ax}[/latex]
19.
[latex]y = \frac{1}{Ax+B}[/latex]
20.
[latex]y = \frac{Ax+B}{Cx+D}[/latex]
21.
[latex]y= \ln(Ax+B)[/latex]
22.
[latex]y = \frac{1}{\ln(Ax+B)}[/latex]
23.
[latex]y = \frac{\ln(Ax+B)}{Ax+B}[/latex]
24.
[latex]y= \ln \bigg( \frac{1}{Ax+B} \bigg)[/latex]
25.
For [latex]y = Ax^2 + Bx + C[/latex], (a) find [latex]y '[/latex], (b) find the value(s) of [latex]x[/latex] so that [latex]y ' = 0[/latex], and (c) find [latex]y ' '[/latex]. (You should recognize the part [b] answer from intermediate algebra. What is it?)
26.
For [latex]y = Ax(B – x) = ABx – Ax^2[/latex], (a) find [latex]y '[/latex], (b) find the value(s) of [latex]x[/latex] so that [latex]y ' = 0[/latex], and (c) find [latex]y ''[/latex].
27.
For [latex]y= Ax^3+Bx^2+C[/latex], (a) find [latex]y '[/latex], (b) find the value(s) of [latex]x[/latex] so that [latex]y ' = 0[/latex], and (c) find [latex]y ''[/latex].
In problems 28 and 29, each quotation is a statement about a quantity of something changing over time.
Let [latex]f(t)[/latex] represent the quantity at time [latex]t[/latex]. For each quotation, tell what [latex]f[/latex] represents and whether the first and second derivatives of [latex]f[/latex] are positive or negative.
28.
(a) “Unemployment rose again, but the rate of increase is smaller than last month.”
(b) “Our profits declined again, but at a slower rate than last month.”
(c) “The population is still rising and at a faster rate than last year.”
29.
(a) “The child’s temperature is still rising, but slower than it was a few hours ago.”
(b) “The number of whales is decreasing but at a slower rate than last year.”
(c) “The number of people with the flu is rising and at a faster rate than last month.”
30.
On which intervals is the function in Fig. 30 (a) concave up and (b) concave down?
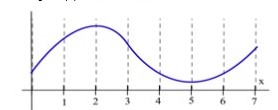
Figure 30
31. On which intervals is the function in Fig. 31 (a) concave up and (b) concave down?
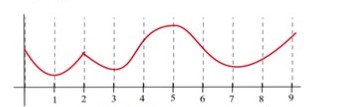
Figure 31
32.
Sketch the graphs of functions that are defined and concave up everywhere and which have
(a) no roots, (b) exactly 1 root, (c) exactly 2 roots, and (d) exactly 3 roots.
In problems 32-36, a function and values of [latex]x[/latex] so that [latex]f '(x) = 0[/latex] are given. Use the second derivative test to determine whether each point [latex](x, f(x)[/latex] is a local maximum, a local minimum, or neither.
33.
[latex]f(x) = 2x^3 – 15x^2 + 6 , x = 0 , 5[/latex]
34.
[latex]g(x) = x^3 – 3x^2 – 9x + 7 , x = –1 , 3[/latex]
35.
[latex]h(x) = x^4 – 8x^2 – 2 , x = –2, 0, 2[/latex]
36.
[latex]f(x) = x \ln(x) , x = 1/e[/latex]
37.
Which of the labeled points in Fig. 37 are inflection points?
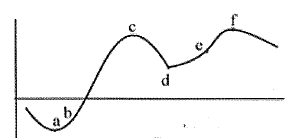
Figure 37
38. Which of the labeled points in Fig. 38 are inflection points?
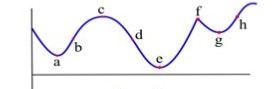
39.
How many inflection points can a
(a) quadratic polynomial have?
(b) cubic polynomial have?
(c) polynomial of degree n have?
40.
Fill in the table with “+”, “–”, or “0” for the function in Fig. 40.
| [latex]x[/latex] | [latex]f(x)[/latex] | [latex]f'(x)[/latex] | [latex]f''(x)[/latex] |
| 0 | |||
| 1 | |||
| 2 | |||
| 3 | |||
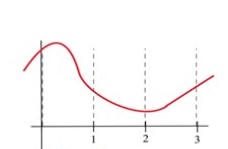
Figure 40
41.
Fill in the table with “+”, “–”, or “0” for the function in Fig. 41
| [latex]x[/latex] | [latex]f(x)[/latex] | [latex]f'(x)[/latex] | [latex]f''(x)[/latex] |
| 0 | |||
| 1 | |||
| 2 | |||
| 3 | |||
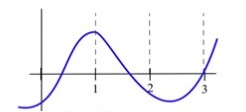
Figure 41
In problems 42–48, find the derivative and second derivative of each function.
42.
[latex]f(x) = 7x^2 + 5x – 3[/latex]
43.
[latex]f(x) = (2x – 8)^5[/latex]
44.
[latex]f(x) = (6x – x^2)[/latex][latex]10[/latex]
45.
[latex]f(x) = x (3x + 7)^5[/latex]
46.
[latex]f(x)=(2x^3+3)^6[/latex]
47.
[latex]f(x)=\sqrt{x^2+6x+1}[/latex]
48.
[latex]f(x)=\ln(x^2+4)[/latex]
49.
Find the equation of the line tangent to [latex]f(x) = e^x[/latex] at the point [latex](3, e^3 )[/latex]. Where will this tangent line intersect the x-axis? Where will the tangent line to [latex]f(x) = e^x[/latex] at the point [latex](p, e^p )[/latex] intersect the x-axis?
50.
Find all extremes of [latex]f(x) = 3x^2 – 12x + 7[/latex] and use the first derivative test to determine if they are maximums, minimums, or neither.
In problems 51–56, find all of the critical points and local maximums and minimums of each function.
51.
[latex]f(x) = x^2 + 8x + 7[/latex]
52.
[latex]f(x) = 2x^2 – 12x + 7[/latex]
53.
[latex]f(x) = x^3 – 6x^2 + 5[/latex]
54.
[latex]f(x) = (x – 1)^2 (x – 3)[/latex]
55.
[latex]f(x) = \ln( x^2 – 6x + 11 )[/latex]
56.
[latex]f(x) = 2x^3 – 96x + 42[/latex]
In problems 57–64, find all critical points and global extremes of each function on the given intervals.
57.
[latex]f(x) = x^2 – 6x + 5[/latex] on the entire real number line.
58.
[latex]f(x) = 2 – x^3[/latex] on the entire real number line.
59.
[latex]f(x) = x^3 – 3x + 5[/latex] on the entire real number line.
60.
[latex]x-e^x[/latex] on the entire real number line.
61.
[latex]f(x) = x^2 – 6x + 5[/latex] on [latex][ –2, 5][/latex].
62.
[latex]f(x) = 2 – x^3 [/latex] on [latex][ –2, 1][/latex].
63.
[latex]f(x) = x^3 – 3x + 5[/latex] on [latex][ –2, 1][/latex].
64.
[latex]x-e^x[/latex] on [latex][ 1, 2][/latex].
65.
Find all of the critical points of the function in Fig. 65 and identify them as local max, local min, or neither. Find the global max and min on the interval.
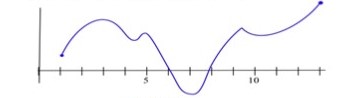
66.
Find all of the critical points of the function in Fig. 66 and identify them as local max, local min, or neither. Find the global max and min on the interval.
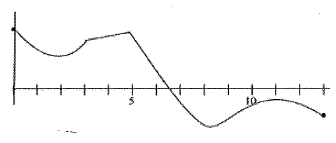
67.
Suppose [latex]f(1) = 5[/latex] and [latex]f '(1) = 0[/latex]. What can we conclude about the point [latex](1,5)[/latex] if
(a) [latex]f '(x) < 0[/latex] for [latex]x < 1[/latex], and [latex]f '(x) > 0[/latex] for [latex]x > 1[/latex]?
(b) [latex]f '(x) < 0[/latex] for [latex]x < 1[/latex], and [latex]f '(x) < 0[/latex] for [latex]x > 1[/latex]?
(c) [latex]f '(x) > 0[/latex] for [latex]x < 1[/latex], and [latex]f '(x) < 0[/latex] for [latex]x > 1[/latex]?
(d) [latex]f '(x) > 0 for x < 1[/latex], and [latex]f '(x) > 0[/latex] for [latex]x > 1[/latex]?
68.
What will the [latex]2nd[/latex] derivative of a quadratic polynomial be? The [latex]3rd[/latex] derivative? The [latex]4th[/latex] derivative?
69.
What will the [latex]3rd[/latex] derivative of a cubic polynomial be? The [latex]4th[/latex] derivative?
70.
What can you say about the nth and [latex](n+1)[/latex]st derivatives of a polynomial of degree [latex]n[/latex]?
71.
Sketch the graph of a continuous function [latex]f[/latex] so that
(a) [latex]f(1) = 3, f '(1) = 0[/latex], and the point [latex](1,3)[/latex] is a local maximum of [latex]f[/latex].
(b) [latex]f(2) = 1, f '(2) = 0[/latex], and the point [latex](2,1)[/latex] is a local minimum of [latex]f[/latex].
(c) [latex]f(5) = 4, f '(5) = 0[/latex], and the point [latex](5,4)[/latex] is not a local minimum or maximum of [latex]f[/latex].
72.
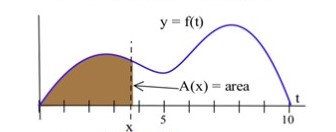
Define [latex]A(x)[/latex] to be the area bounded between the x-axis, the graph of [latex]f[/latex], and a vertical line at [latex]x (0 \leq x \leq 10 )[/latex]. See Fig. 72.
(a) At what value of [latex]x[/latex] is [latex]A(x[/latex]) minimum?
(b)At what value of [latex]x[/latex] is [latex]A(x)[/latex] maximum?
73.
Define S(x) to be the slope of the line through the points (0,0) and (x, f(x)). See Fig. 73.
(a) At what value of x is S(x) minimum?
(b) At what value of x is S(x) maximum?
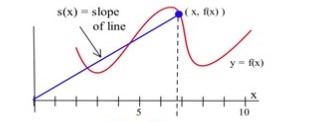
Figure 73
74.
(a) You have [latex]200[/latex] feet of fencing to enclose a rectangular vegetable garden. What should the dimensions of your garden be in order to enclose the largest area?
(b) Show that if you have P feet of fencing available, the garden of the greatest area is a square.
(c) What are the dimensions of the largest rectangular garden you can enclose with P feet of fencing if one edge of the garden borders a straight river and does not need to be fenced?
(d) Just thinking (calculus will not help with this one): What do you think is the shape of the largest garden that can be enclosed with P feet of fencing if we do not require the garden to be rectangular? What do you think is the shape of the largest garden that can be enclosed with P feet of fencing if one edge of the garden borders a river and does not need to be fenced?
75.
(a) You have [latex]200[/latex] feet of fencing available to construct a rectangular pen with a fence divider down the middle (see Fig. 75). What dimensions of the pen enclose the largest total area?
(b) If you need [latex]2[/latex] dividers, what dimensions of the pen enclose the largest area?
(c) What are the dimensions in parts (a) and (b) if one edge of the pen borders on a river and does not require any fencing?

Figure 75
76.
You have [latex]120[/latex] feet of fencing to construct a pen with [latex]4[/latex] equal-sized stalls. If the pen is rectangular and shaped like the one in Fig. 76, what are the dimensions of the pen of the largest area and what is that area?
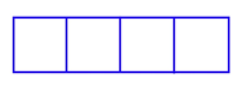
Figure 76
77.
Suppose you decide to fence the rectangular garden in the corner of your yard. Then two sides of the garden are bounded by the yard fence, which is already there, so you only need to use the 80 feet of fencing to enclose the other two sides. What are the dimensions of the new garden of largest area? What are the dimensions of the rectangular garden of largest area in the corner of the yard if you have F feet of new fencing available?
78.
(a) You have been asked to bid on the construction of a square-bottomed box with no top that will hold 100 cubic inches of water. If the bottom and sides are made from the same material, what are the dimensions of the box that uses the least material? (Assume that no material is wasted.)
(b) Suppose the box in part (a) uses different materials for the bottom and the sides. If the bottom material costs 5¢ per square inch and the side material costs 3¢ per square inch, what are the dimensions of the least expensive box that will hold 100 cubic inches of water?
79.
Problem 78 is a “classic” problem that has many variations. We could require that the box be twice as long as it is wide, or that the box have a top, or that the ends cost a different amount than the front and back, or even that it costs some amount of money to weld each inch of edge. Write and solve a variation of Problem 78.
80.
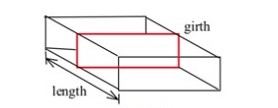
U.S. postal regulations state that the sum of the length and girth (distance around) of a package must be no more than 108 inches (Fig. 80).
(a) Find the dimensions of the acceptable box with a square end that has the largest volume.
(b) Find the dimensions of the acceptable box which has the largest volume if its end is a rectangle twice as long as it is wide.
81.
D. Simonton claims that the “productivity levels” of people in different fields can be described as a function of their “career age” [latex]t[/latex] by [latex]p(t) = e^{–at} – e ^{–bt}[/latex], where [latex]a[/latex] and [latex]b[/latex] are constants that depend on the field of work, and career age is approximately [latex]20[/latex] less than the actual age of the individual.
(a) Based on this model, at what ages do mathematicians ([latex]a=.03, b=.05)[/latex], geologists [latex](a=.02, b=.04)[/latex], and historians [latex](a=.02, b=.03)[/latex] reach their maximum productivity?
(b) Simonton says, “With a little calculus we can show that the curve ([latex]p(t)[/latex]) maximizes at [latex]t =\frac{1}{b-a}\ln(\frac{b}{a})[/latex].” Use calculus to show that Simonton is correct.
Note: Models of this type have uses for describing the behavior of groups, but it is dangerous and usually invalid to apply group descriptions or comparisons to individuals in the group.
(Scientific Genius, by Dean Simonton, Cambridge University Press, 1988, pp. 69–73)
82.
You own a small airplane that holds a maximum of [latex]20[/latex] passengers. It costs you [latex]\$100[/latex] per flight from St. Thomas to St. Croix for gas and wages plus an additional [latex]\$6[/latex] per passenger for the extra gas required by the extra weight. The charge per passenger is [latex]\$30[/latex] each if [latex]10[/latex] people charter your plane ([latex]10[/latex] is the minimum number you will fly), and this charge is reduced by [latex]\$1[/latex] per passenger for each passenger over [latex]10[/latex] who goes (that is, if [latex]11[/latex] go they each pay[latex]\$29[/latex], if [latex]12[/latex] go they each pay [latex]\$28[/latex], etc.). What number of passengers on a flight will maximize your profits?
83.
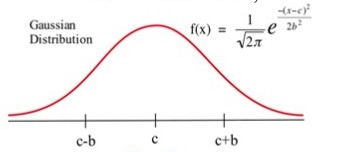
The function is called the Gaussian distribution, and its graph is a bell-shaped curve
(Fig. 83) that occurs commonly in statistics.
(i) Show that f has a maximum at [latex]x = c[/latex]. (The value c is called the mean of this distribution.)
(ii) Show that f has inflection points where [latex]x = c + b[/latex] and [latex]x = c – b[/latex]. (The value b is called the standard deviation of this distribution.)
84.
In the planning of a coffee shop, we estimate that if there is seating for between [latex]40[/latex] and [latex]80[/latex] people, the daily profit will be [latex]\$50[/latex] per seat. However, if the seating capacity is more than [latex]80[/latex] places, the daily profit per seat will be decreased by [latex]\$1[/latex] for each additional seat over [latex]80[/latex]. What should the seating capacity be in order to maximize the coffee shop’s total profit?
85.
In the planning of a taco restaurant, we estimate that if there is seating for between [latex]10[/latex] and [latex]40[/latex] people, the daily profit will be [latex]\$10[/latex] per seat. However, if the seating capacity is more than [latex]40[/latex] places, the daily profit per seat will be decreased by [latex]\$0.20[/latex] per seat. What should the seating capacity be in order to maximize the taco restaurant’s total profit?
86.
The total cost in dollars for Alicia to make q oven mitts is given by [latex]C(q) = 64 + 1.5q+0.1q^2[/latex].
(a) What is the fixed cost?
(b) Find a function that gives the marginal cost.
(c) Find a function that gives the average cost.
(d) Find the quantity that minimizes the average cost.
(e) Confirm that the average cost and marginal cost are equal at your answer to part (d).
87.
Shaki makes and sells backpack danglies. The total cost in dollars for Shaki to make [latex]q[/latex] danglies is given by [latex]C(q) = 75+2q+0.015q^2[/latex]. Find the quantity that minimizes Shaki’s average cost for making danglies.
88.
If [latex]g(20)= 35[/latex] and [latex]g'(20)= -2[/latex], estimate the value of [latex]g(22)[/latex].
89.
If [latex]g(1)= -17[/latex] and [latex]g'(1)= 5[/latex], estimate the value of [latex]g(1.2)[/latex].
90.
Use the tangent line approximation to estimate the cube root of [latex]9[/latex].
91.
Use the tangent line approximation to estimate the fifth root of [latex]30[/latex].
92.
The demand function for Alicia’s oven mitts is given by [latex]q=-8p+80[/latex] ([latex]q[/latex] is the number of oven mitts, [latex]p[/latex] is the price in dollars). Find the elasticity of demand when [latex]p = \$7.50[/latex]. Will revenue increase if Alicia raises her price from [latex]\$7.50[/latex]?
93.
The demand function for Shaki’s danglies is given by [latex]q=-35p+205[/latex] ([latex]q[/latex] is the number of danglies, [latex]p[/latex] is the price in dollars per dangly). Find the elasticity of demand when [latex]p = \$5[/latex]. Should Shaki raise or lower his price to increase revenue?

