Chapter 1: Algebra Review
Section 1.5 Quadratics
Learning Objectives
By the end of this section, the student should be able to:
- Learn basic concepts and different forms of a quadratic function and their graphs.
- Solve problems involving quadratic equations.
Quadratics
Quadratics are transformations of the function [latex]f(x)=x^2[/latex]. Quadratics commonly arise from problems involving area and projectile motion, providing some interesting applications.
Example 1
A backyard farmer wants to enclose a rectangular space for a new garden. She has purchased [latex]80[/latex] feet of wire fencing to enclose three sides and will put the fourth side against the backyard fence. Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length [latex]L[/latex].
In a scenario like this involving geometry, it is often helpful to draw a picture. It might also be helpful to introduce a temporary variable, [latex]W[/latex], to represent the side of fencing parallel to the fourth side or backyard fence.
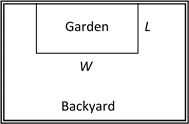
Since we know we only have [latex]80[/latex] feet of fence available, we know that [latex]L+W+L=80[/latex], or more simply, [latex]2L+W=80[/latex]. This allows us to represent the width, [latex]W[/latex], in terms of [latex]L[/latex]: [latex]W=80-2L[/latex].
Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so [latex]A=LW=L(80-2l)[/latex], so [latex]A(L)=80L-2L^2.[/latex] This formula represents the area of the fence in terms of the variable length [latex]L[/latex].
Forms of Quadratic Functions
The standard form of a quadratic function is [latex]f(x)=ax^2+bx+c[/latex].
The transformation form of a quadratic function is [latex]f(x)=a(x-h)^2+k[/latex].
The vertex of the quadratic function is located at [latex](h, k)[/latex], where [latex]h[/latex] and [latex]k[/latex] are the numbers in the transformation form of the function. Because the vertex appears in the transformation form, it is often called the vertex form.
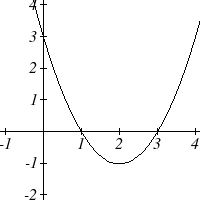
Example 2
Write an equation for the quadratic graphed below as a transformation of [latex]f(x)=x^2[/latex].
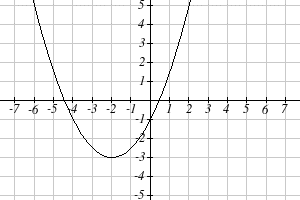
We can see the graph is the basic quadratic shifted to the left [latex]2[/latex] and down [latex]3[/latex], putting the vertex at [latex](-2, -3)[/latex], giving a formula in the form [latex]g(x)=a(x+2)^2-3[/latex]. By plugging in a point that falls on the grid, such as [latex](0, -1)[/latex], we can solve for the stretch factor:
[latex]\begin{align*} -1=&a(0+2)^2-3 \\ 2=& 4a \\ a=& \frac{1}{2} \end{align*}[/latex]
The equation for this formula is [latex]g(x)=\frac{1}{2}(x+2)^2-3.[/latex]
Video
Short Run Behavior: Intercepts
As with any function, we can find the vertical intercepts of a quadratic by evaluating the function at an input of zero, and we can find the horizontal intercepts by solving for when the output will be zero. Notice that depending upon the location of the graph, we might have zero, one, or two horizontal intercepts.
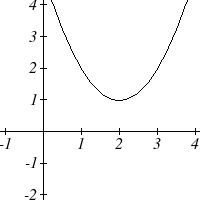
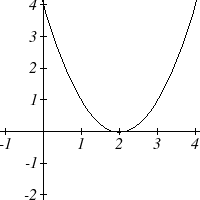
Notice that in the standard form of a quadratic, the constant term c reveals the vertical intercept of the graph, since [latex]f(0)=a(0)^2+b(0)+c=c[/latex].
Example 3
Find the vertical and horizontal intercepts of the quadratic [latex]f(x)=3x^2+5x-2[/latex].
We can find the vertical intercept by evaluating the function at an input of zero: [latex]f(0)=3(0)^2+5(0)-2=-2.[/latex] So the vertical intercept is at [latex](0, -2)[/latex].
For the horizontal intercepts, we solve for when the output will be zero: [latex]0=3x^2+5x-2.[/latex] In this case, the quadratic can be factored easily, providing the simplest method for solution: [latex]0=(3x-1)(x+2),[/latex] so either
[latex]\begin{align*} 0=& 3x-1\\ x=& \frac{1}{3} \end{align*}[/latex]
or
[latex]\begin{align*} 0=& x+2\\ x=& -2 \end{align*}[/latex]
So the horizontal intercepts are at [latex]\left(\frac{1}{3},0\right)[/latex] and [latex](-2,0)[/latex].
Quadratic Formula
When a quadratic is not factorable or is hard to factor, we can turn to the quadratic formula.
For a quadratic function given in standard form [latex]f(x)=ax^2+bx+c[/latex], the quadratic formula gives the horizontal intercepts of the graph of this function: [latex]x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.[/latex]
Video
Example 4
A ball is thrown upward from the top of a [latex]40[/latex]-foot-high building at a speed of [latex]80[/latex] feet per second. The ball’s height above ground can be modeled by the equation [latex]H(t)=-16t^2+80t+40.[/latex] When does the ball hit the ground?
To find when the ball hits the ground, we need to determine when the height is zero, i.e., when [latex]H(t) = 0[/latex]. While we could do this using the transformation form of the quadratic, we can also use the quadratic formula: [latex]t=\frac{-80\pm \sqrt{80^2-4(-16)(40)}}{2(-16)}=\frac{-80\pm\sqrt{8960}}{-32}.[/latex]
Since the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions: [latex]t=\frac{-80-\sqrt{8960}}{-32}\approx 5.458 \quad\text{or}\quad t=\frac{-80+\sqrt{8960}}{-32}\approx -0.458.[/latex]
The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about [latex]5.458[/latex] seconds.
Vocabulary
Media Attributions
- image096
- image057-1
- image058
- image059
- image060
A polynomial having degree 2 and it is a continuous function of the form f(x)=ax^2+bx+c where a is not equal to 0
Standard form of quadratic f(x)=ax^2+bx+c .
vertex form of a quadratic f(x)=a(x-h)^2+k
Vertical intercepts, also known as y-intercepts, refer to the points where a graph intersects the y-axis. These points have an x-coordinate of zero and can be found by setting x equal to zero and solving for y. In other words, they are the points on a graph where the input or independent variable has a value of zero, and the output or dependent variable takes a certain value.
x equals negative b plus or minus the square root of b squared minus 4ac all over 2a.
a vertical line drawn through the vertex of a parabola, that opens up or down, around which the parabola is symmetric; it is defined by x = −b / 2a.
A polynomial of degree two which can be written in the form f(x) = ax^2 + bx + c

