Chapter 1: Algebra Review
Chapter 1 Review Problems
Review Problems
1. Use the rules of exponents to simplify the following. Write your answer using only positive exponents. Assume all variables represent non-zero numbers.
a. [latex]\frac{4y^3}{12y^7}[/latex]
b. [latex]\bigg(m^{-2} \bigg)^3[/latex]
c. [latex]\bigg( xyz \bigg)^8[/latex]
d. [latex]\bigg(2xy^{-3}z^0 \bigg)^3[/latex]
e. [latex]\bigg(5x^3\bigg) \bigg(-7x^5 \bigg)[/latex]
f. [latex]\sqrt[4]{(4ab^2)^4 (b^{-3})^{-2} }[/latex]
2. Write the equation of the line that is parallel to and has y-intercept [latex]y = 1.5x-11[/latex] at [latex]y = 3[/latex].
3. Write the equation of the line that passes through the points [latex](1, 5)[/latex] and [latex](3, 11).[/latex]
4. A coffee supplier finds that it costs [latex]\$850[/latex] to roast and package [latex]100[/latex] pounds of coffee in a day and [latex]\$2850[/latex] to produce [latex]500[/latex] pounds of coffee in a day. Assume that the cost function is linear. Express the cost as a function of the number of pounds of coffee they produce each day.
5. Factor [latex]y^5-6y^4+9y^3[/latex].
6. Factor [latex]a^4-5a^2-36[/latex].
7. The two points [latex](-3, \frac{5}{8} )[/latex] and [latex](2,20)[/latex] both lie on the graph of a function.
- Find the formula [latex]y = g(x)[/latex] for if it is a linear function.
- Find the formula [latex]y = g(x)[/latex] for if it is of the form [latex]g(x) = Ca^x[/latex].
8. An object is thrown into the air. Its height in feet above the ground [latex]t[/latex] seconds later is given by [latex]h(t) = -16t^2+30t+25[/latex].
- Find the time when the object reaches its maximum height.
- How high does it get?
- When does it land?
- The graph of [latex]y = h(t)[/latex] is a parabola. What is the physical meaning of the [latex]y[/latex]-intercept of this parabola? (That is, what does the [latex]y[/latex]-intercept of the parabola tell us about the object?)
9. Suppose [latex]\bigg( u \circ v \bigg) (x) = \frac{1}{x^2}+1[/latex] and [latex]\bigg( v \circ u \bigg) (x) = \frac{1}{(x+1)^2}[/latex]. Find possible formulas for [latex]u(x)[/latex] and [latex]u(x)[/latex].
10. Suppose [latex]f(x) = x^2-2x[/latex]:
- Compute [latex]\frac{f(x)-f(3)}{x-3}[/latex]. Simplify your answer.
- In English, what is the meaning of your answer to part a?
- Graphically, what is the meaning of your answer to part a?
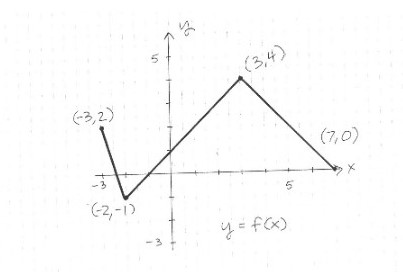
10. Here is the graph of [latex]y = f(x)[/latex]. Use this graph to sketch the graph on graph paper of [latex]y = -3f(x-2)[/latex]. Be careful and neat, and remember to label your graph. Briefly explain what you did to find the graph.
11. In [latex]2000[/latex], the number of people infected by a virus was [latex]P_0[/latex]. Due to a new vaccine, the number of infected people has decreased by 14% each year since 2000.
- Find a formula for [latex]P = f(n)[/latex], the number of infected people [latex]n[/latex] years after [latex]2000[/latex].
- When will there be (or when were there) just half as many people infected as there were in [latex]2000[/latex]?
12. Here is the graph of an exponential or logarithmic function.
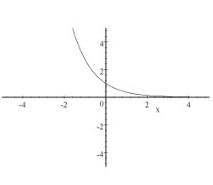
- Is this an exponential function with base [latex]b > 1[/latex], an exponential function with [latex]0 b 1[/latex], or a logarithmic function with base [latex]b > 1[/latex]?
- What is the value of [latex]b[/latex] (the base) for this graph? How do you know?
Brief Answers to Selected Exercises
1.
- [latex]\frac{4y^3}{12y^7}[/latex]
- [latex]\bigg( 2xy^{-3} z^0 \bigg) ^3 = \frac{8x^3}{y^9}[/latex]
- [latex]\sqrt[4]{(4ab^2)^4(b^{-3})^{-2}}= 4ab^{\frac{7}{2}}[/latex]
3.
[latex]y= 3x+2[/latex]
4.
[latex]C(n) = 5n+350[/latex], where [latex]C[/latex] is the cost in dollars and [latex]n[/latex] is the number of pounds of coffee produced.
5. [latex]y^3(y-3)^2[/latex]
7.
- [latex]g(x) = \frac{31}{8}x - \frac{49}{4}[/latex]
- [latex]g(x) = 5.2^x[/latex]
9. [latex]u(x) = x+1 \ ; \ v(x) = \frac{1}{x^2}[/latex]
11. The graph is the same basic shape, but it is upside down, 3 times as tall, and shifted 2 units to the right. The four labeled points are now [latex](-1, -6), (0, 3), (5, -12[/latex]), and [latex](9, 0)[/latex].
12.
- This is exponential decay, so an exponential function with [latex]0 b 1[/latex].
- (You have to estimate here. Your answer might be different from mine.) It looks to me as if when [latex]x = -1[/latex], [latex]y[/latex] is about [latex]2.8[/latex], so I will guess that this is [latex]y = \frac{1}{e^x} = e^{-x}[/latex].
Media Attributions
- reviewchapter1_a
- reviewchapter1_b

